基于高斯消元的BATS码的改进译码算法*

杨 娟，嵇建波，李海兵

（桂林航天工业学院，广西 桂林 541004）

0 引 言

近年来，无线通信在世界范围内迅速发展，并且诸如移动TV、推送型信息等无线服务已广泛应用于实际生活。其中，多播和广播是此类应用中的常见操作，引起了研究者的极大兴趣。然而，由于无线信道衰落和信号干扰，多播网络的数据传输变得不可靠。为了提高网络的可靠性，杨伟豪和张珍提出网络编码（Network Coding，NC）的思想，即允许中间节点对输入数据包进行编码。网络编码在增强无线网络可靠性的同时，实现了更高的网络吞吐量。然而，网络编码在提升可靠性和吞吐量等性能的同时，也面临着系数开销大、长延迟等问题，使其无法广泛应用于实际生活。

为了平衡编码开销/译码复杂度和吞吐量问题，Shenghao Yang等人于2011年提出了批量稀疏码（Batched Sparse Codes，BATS Codes）[1-2]的概念。BATS码是一种将喷泉码[3-5]和网络编码相结合的一种新型编译码方案，在发送端将要传送的数据信息分成特定长度的源数据包，根据度分布函数选出源数据包并对其进行外码编码，生成以批次为单位的编码包在信道上进行传输。在中继节点，对接收到的批次进行批次内的随机线性网络编码后传输到接收端。经过信道传输后，接收端不需要考虑信道条件，只要保证接收到足够数量的批次，就一定可以成功译码，从而恢复要传送的源数据信息。BATS码作为一种较新颖的信道编码技术，继承了喷泉码和网络编码的优点。凭借其无码率特性和无需反馈、中断可续传、吞吐量高、安全性高、复杂度低等优点，近些年成为通信领域研究的热点[6]。

BATS码在BP译码方式下的渐进译码性能分析已经在文献[7-8]中描述过，当原始数据包趋近无限长时，BP译码器可以以较高概率恢复固定比例（接近1）的原始输入包，但是当原始数据包数量有限时，译码性能将会有较大幅度衰减[9-10]。因此，在接收端计算资源充足的情况下，可以考虑在BP译码后级联高斯消元译码算法[11]。采用高斯消元算法，当矩阵满秩时可将输入数据包译出，但如果矩阵不满足满秩的条件，系数矩阵对应的输入数据包则完全译不出。推荐的算法利用当系数矩阵不满秩时也存在部分可译包的事实，识别并判断这些可译包并将其译出，从而提高高斯消元的译码性能。

1 BATS码的编译码原理

编码BATS码在大小为q的有限域F中，对K个原始数据包进行编码，每个数据包有T个符号。每个包可表示为FT中的一个列向量，因此可以将K个输入的原始数据包用矩阵表示：

其中bi是第i个包，因此B也可以看作是输入数据包的集合。

在发送端，首先对度分布进行采样，得到一个整数di。在B中随机选择di个输入包构成Bi。将这di个包进行随机线性组合得到一个批次，每个批次包括M个编码包。这个过程可用下述矩阵方程进行表示：

按顺序依次生成各个批次，并由发送端发送至中间节点。在中间节点，采用随机网络线性编码对每一个批次进行批次内部再编码。网络中，假设每个批次的端到端传输是线性操作，给定一个目的节点，Hi是第i个批次的转移矩阵，Yi是其对应批次的输出数据包，可以得到：

转移矩阵Hi与内码编码和网络的拓扑结构有关，不同的批次对应的Hi可以不同。假设Hi在接收端是已知的。事实上，在线性网络编码中，在目的节点确实可以通过存放于包头的系数向量获得转移矩阵的信息。

上述外码和内码的编码方法可以用唐纳图描述，如图1所示，有K个变量节点。变量节点用实心圆表示，其中变量节点i对应第i个原始数据包bi；方块表示校验节点也就是批次码，其中校验节点j对应第j个批次Yj。如果bi参与了Yj的生成，则说明校验节点j与变量节点i相连。与每个校验节点j相关的是生成矩阵Gj，Hj表示转移矩阵。

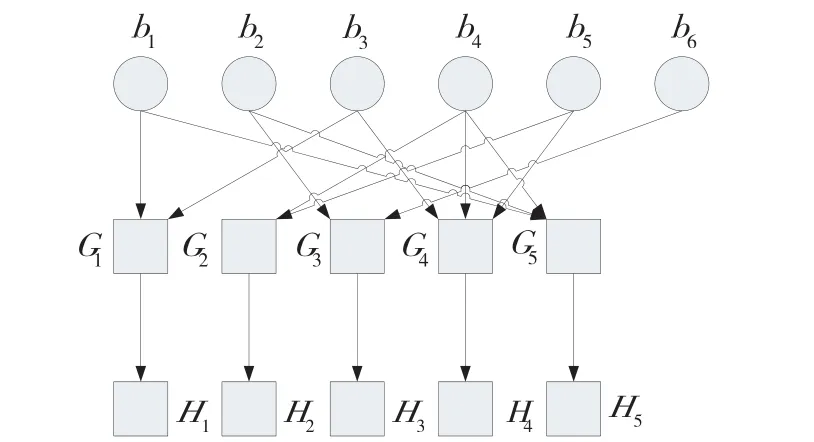
图1 BATS codes的唐纳图

在接收端，首先由BP译码器对接收到的批次码进行译码。由式（3）可知，目的节点可以通过Yi、Gi和Hi的信息进行译码得到Bi，其中i=1,2,…,n。译码过程等价于求解式（3）对应的线性系统方程组。BP译码过程可以由图2进行直观描述，第一行是变量节点代表输入数据包，第二行是校验节点表示接收到的各个批次码，整体转移矩阵GiHi与校验节点i相关联。

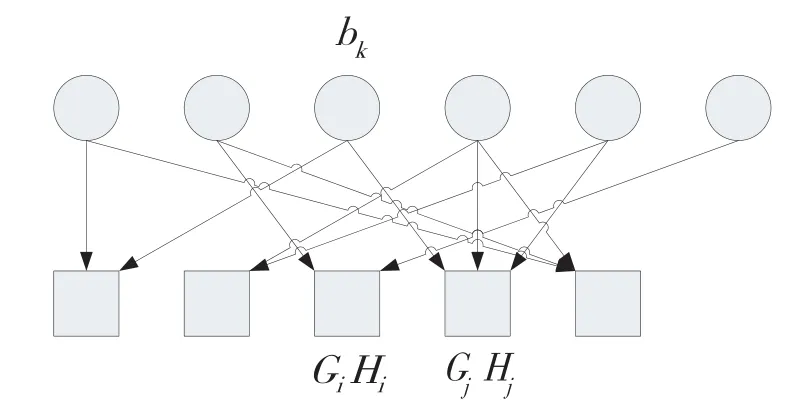
图2 译码图

当第i个校验节点的秩rk(GiHi)等于它的度di时，校验节点i是可译的。因此，Bi可以通过解方程Yi=BiGiHi恢复，且得到的是唯一解。当恢复出Bi中的di个原始数据包后，将这些恢复出的原始包替换到还未译码的批次中。假设bk在Bi中，如果只有一条边与变量节点k相连，边的另一个顶点是校验节点i，此时直接移除变量节点k，它不再参与后续译码过程；如果变量节点k还与校验节点j相连且j≠i，通过替换过程，校验节点j的度数降1，并删除Gj中对应于变量节点k的那一行。在译码图中，这个过程相当于首先删除校验节点i以及与之相连的变量节点，然后更新与该变量节点相连的其他校验节点的信息，重复这些步骤直至没有可解的校验节点，最终译码得到原始输入数据包。

图3 当矩阵满秩时的高斯消元过程

当BP译码算法停止后，可以将剩下的未译出的批次码的系数矩阵合并成一个系数矩阵。如果合并后的系数矩阵是满秩的，对其采用高斯消元算法可以将剩下的输入数据包译出，否则如果系数矩阵不满秩，则高斯消元算法无解，译码过程停止。考虑一个线性系统Y=AX，传统的高斯消元算法的步骤包括两个过程[12-13]，分别是三角化过程和标准化过程：（1）三角化过程：运用初等行（列）变换将系数矩阵转化为行阶梯型矩阵，如图3所示，将图3（a）中对应的矩阵转化为图3（b）所示矩阵，该矩阵为对角矩阵；（2）标准化：当三角化过程结束后，运用初等行变换将行阶梯型矩阵转化为最简行阶梯型矩阵，如图3（c）转变为图3（d）所示矩阵。当矩阵满秩时，系数矩阵的最简行阶梯型矩阵即为一个单位矩阵。将线性系统的系数矩阵化为单位阵后，即可求得X中对应的输入数据包。

传统的高斯消元算法只能在当系数矩阵A满秩时，才能求解出线性系统对应的未知量X，否则当矩阵A的秩小于矩阵的列数时，线性系统无解，也就无法译出剩余的输入数据包。但是，经观察发现，某些情况下，当系数矩阵不满秩时，也有可能出现部分未知量可译的情况，这种情况的例子将在下节给出，因此本文利用这一特点优化了高斯消元算法，以提高BATS码的译码性能。

2 改进型的BATS码高斯消元译码算法

在传统的高斯消元算法描述中，当系数矩阵不是满秩的情况下，线性系统无解。但是，通过观察可以发现，当系数矩阵不满秩时，有些情况下，存在部分未知量可以先行译出的现象。例如，如图4所示，对图4（a）矩阵采用高斯消元算法。首先，运用初等行（列）变换将图4（a）所示矩阵转化为行阶梯型矩阵，得到如图4（c）所示矩阵，再将图4（c）所示矩阵转化为最简行阶梯型矩阵，如图4（d）所示。在图4（d）中可以看到，当最简行阶梯型矩阵中存在某一行非零首元为1且同一行中剩下的元素都为零的情况时，该行所对应的未知量也就是BATS码中该行所对应的输入数据包一定可以被译出。

图4 当矩阵不满秩时的高斯消元过程

因此，当BP译码算法停止时，可以将剩下的批次码所对应的系数矩阵合并，计算该矩阵的秩。如果是满秩的，则将所有的输入数据包译出。如果不满秩，对其采用高斯消元算法，将系数矩阵转化为最简行阶梯型矩阵后，检测是否存在可译出的输入数据包。如果有，则将这些可译包先行译出，否则译码过程停止。采用这种方法可以提高传统高斯消元算法的译码成功率。为了验证算法的有效性，下面将用Matlab软件对传统高斯消元算法和本位推荐的改进型高斯消元算法进行仿真和对比，仿真结果最终验证了推荐算法的有效性。

3 仿真结果

考虑如图5所示为两跳的删除信道，s表示发送端，t表示接收端，删除概率e=0.2。BATS码参数设置为q=32，L=2，M=4。当BATS码码长K为30时，如图6所示，横坐标表示发送端发送的批次数，纵坐标表示译码成功率，译码成功率由式K译码成功的输入数据包/K计算得到。图7为当 BATS码码长为10时，传统高斯消元算法和改进型高斯消元算法的译码性能比较图。由图6和图7可以清楚看到，改进型译码算法性能明显优于传统算法。

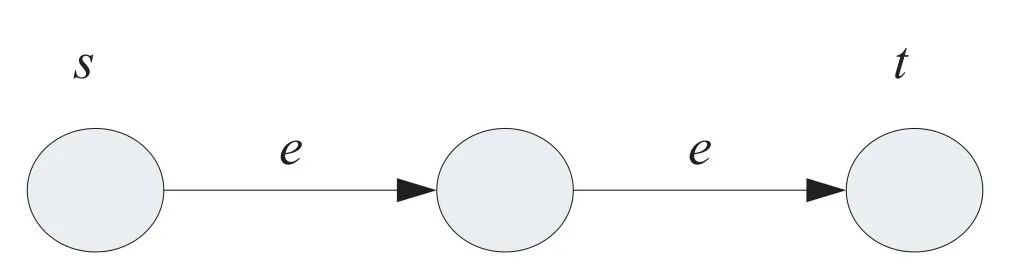
图5 两跳的删除信道

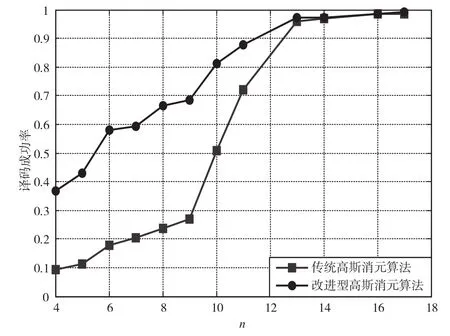
图6 当BATS码码长为30时，传统译码算法与改进型译码算法的译码性能比较

4 结 语

针对BATS码的译码提出了一种基于高斯消元算法的优化改进算法，利用矩阵在不满秩的情况下仍然可能存在可译包的事实，优化原有的传统高斯消元算法，在BP译码算法停止后，检测到系数矩阵不满秩的情况下，不停止译码过程，而是继续采用高斯消元算法检测是否存在可译包，如果存在则将其译出。这种方法能够有效提升BATS码的译码性能，仿真结果也验证了这一结论。