幅度与相位分步识别的QAM调制模式识别算法*

黄思嘉，杜庆治，龙 华，邵玉斌

（昆明理工大学 信息工程与自动化学院，云南 昆明 650504）

0 引 言

自动调制分类（Automatic Modulation Classification，AMC）是无线通信的关键技术之一，调制模式识别在协作和非协作通信领域都有着广泛应用，如自适应通信系统、频谱监测、认知无线电和基于软件无线电的智能接收机和电子战等[1-2]。

由于具有较高的频谱效率，多进制正交幅相调 制（Multiple Quadrature Amplitude Modulation，MQAM）信号在卫星和微波通信中得到了广泛应用。针对该类信号调制方式的识别问题，一直以来都是研究的热点。最早这类信号的调制模式识别多是基于聚类法等方法，如奚家熹等[3]对信号幅值做减法聚类，并根据聚类中心数目判定信号的调制方式。近年来，兴起的神经网络算法对于调制模式识别也有重要的意义，但是在QAM识别领域，神经网络算法大多数是通过把信号的星座图送入卷积神经网络进行识别的[4-5]。之后，很多人利用星座图进行模式识别[6]。这些方法虽然准确率高，但是对于星座图的还原要求比较苛刻。能否正确还原出星座图决定了神经网络是否能够正确识别出信号，并且在低信噪比下识别效果不理想。很多研究人员通过改变神经网络结构来提高识别率。

本文提出了一种幅度相位分步识别的方法来识别QAM信号的调制模式。由于完全还原星座图和消除频偏相偏并不是一件容易的事情，本文利用未消除频偏相偏的星座图进行调制模式识别。

先利用CNN神经网络识别出未消除频偏相偏星座图的幅度层数对信号进行第一次分类，再检测每个信号点的瞬时相位进行差分，得到每个点之间相位跳变幅度。经过减法聚类确定相位跳变次数，由此对信号在相位上进行二次分类，最后识别出QAM信号的调制模式。

该方法虽然步骤比传统方法繁琐，但是不依赖信号的频偏消除和相偏消除，所以能够起到很好的抗频偏作用。此外，因为没有频偏消除和相偏消除的步骤，所以不至于信号在频偏消除和相偏消除等预处理过程中损失信息量。经过试验，这种方法在识别率上比传统的神经网络识别方法在低信噪比下有更好的识别率。

1 信号预处理

1.1 信号模型

获取的QAM信号一般可以表示如下：

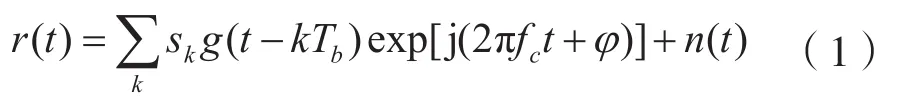
其中，sk表示信号源第k个符号周期发射的符号；QAM信号可以表示为sk=ak+jbk，ak为实部，bk为虚部，j为虚数单位；g(t)为脉冲形成滤波器的冲击响应；Tb为符号周期或码元宽度；fc和φ分别为载波频率和相位；n(t)为高斯白噪声。

1.2 信号载频估计

其中R(f)为接收序列的功率谱密度函数，fs为采样频率，N为采样点数。

1.3 基带信号还原

在估算完载波频率后，可以把信号分为IQ两路，之后进行基带信号还原，得到含有载波频偏和载波相偏的基带信号，其中I、Q分路分别为：

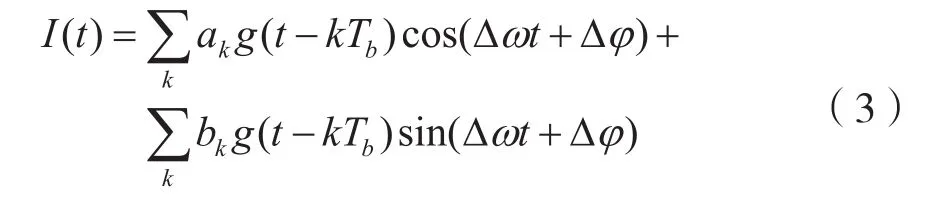
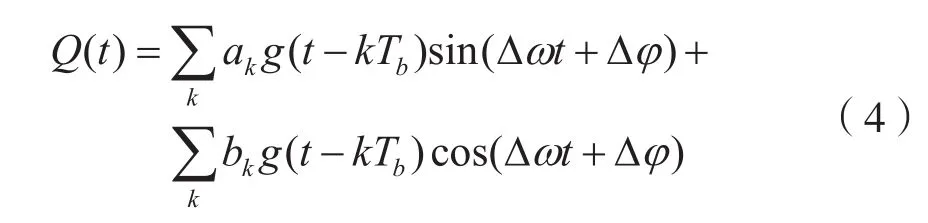
其中，Δω为频偏，Δφ为相偏移。基带信号x(t)可以表示为：

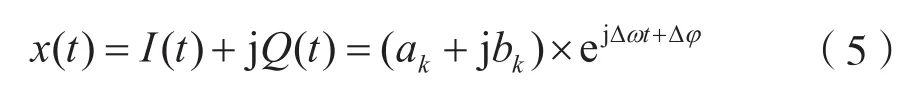
若信号带有白噪声，则为：

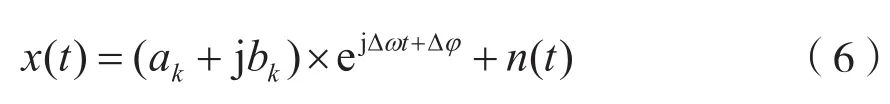
但是因为载波估计的不准确，所以预处理后还原的基带信号其实是带有频偏和相偏的，因为频偏的累计本来应该成散点分别的星座图会因此发生旋转。

1.4 频偏估计

离散处理后的信号，可以表示为：

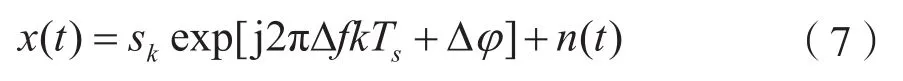
其中Ts为采样间隔，n(k)为白噪声。根据文献[7]中的方法，对信号x(k)做M次方运算，具有去调制的作用，x(k)M可视为频率为MΔf的周期信号，Δω=2πΔfTs。该频率估计问题可采用非线性最小二乘方法，公式为：

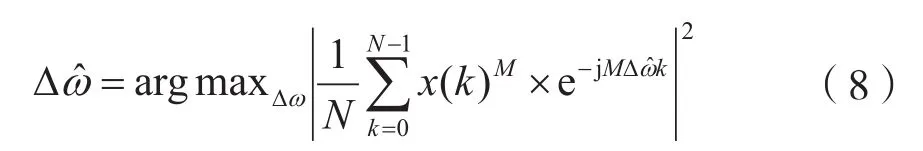
当然，实际上也可以通过对x(k)M做傅里叶变换求出傅里叶变换的峰值点，峰值点所在的位置即MΔf，这样也可以估计出频偏Δf。

1.5 相偏估计

不考虑载频偏差影响时，相位偏移Δφ将使信号散点图整体旋转一个角度，该旋转将使其与信号星座图难以匹配。利用已经估计出的频偏参数，相偏估计的公式为：

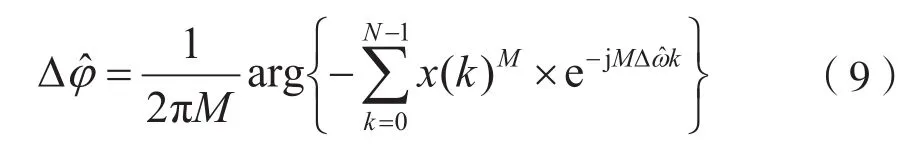
1.6 星座图还原

获取了频偏与相偏的估计值后，就可以还原星座图。图1为还原的几种信号在25 dB与0 dB白噪声下的星座图。

从图1可以看出，不同信号星座图具有明显的图像特征。因此，已有研究将星座图送入CNN网络进行识别，取得了良好的效果[6-11]。但是，在低信噪比下，点数过多的QAM图像将很难区分。如图1（c）和图1（d）所示，在低信噪比环境中很难把16QAM和64QAM等信号很好地区分开。这种方法要求信号的频偏和相偏消除干净才可以送入神经网络识别，所以不具备良好的抗频偏和抗相偏能力。很多文章通过改变神经网络的结构提高低信噪比下的识别率和抗频偏和相偏的能力[4-5,8]，本文则提出了一种联合聚类法的模式识别算法。

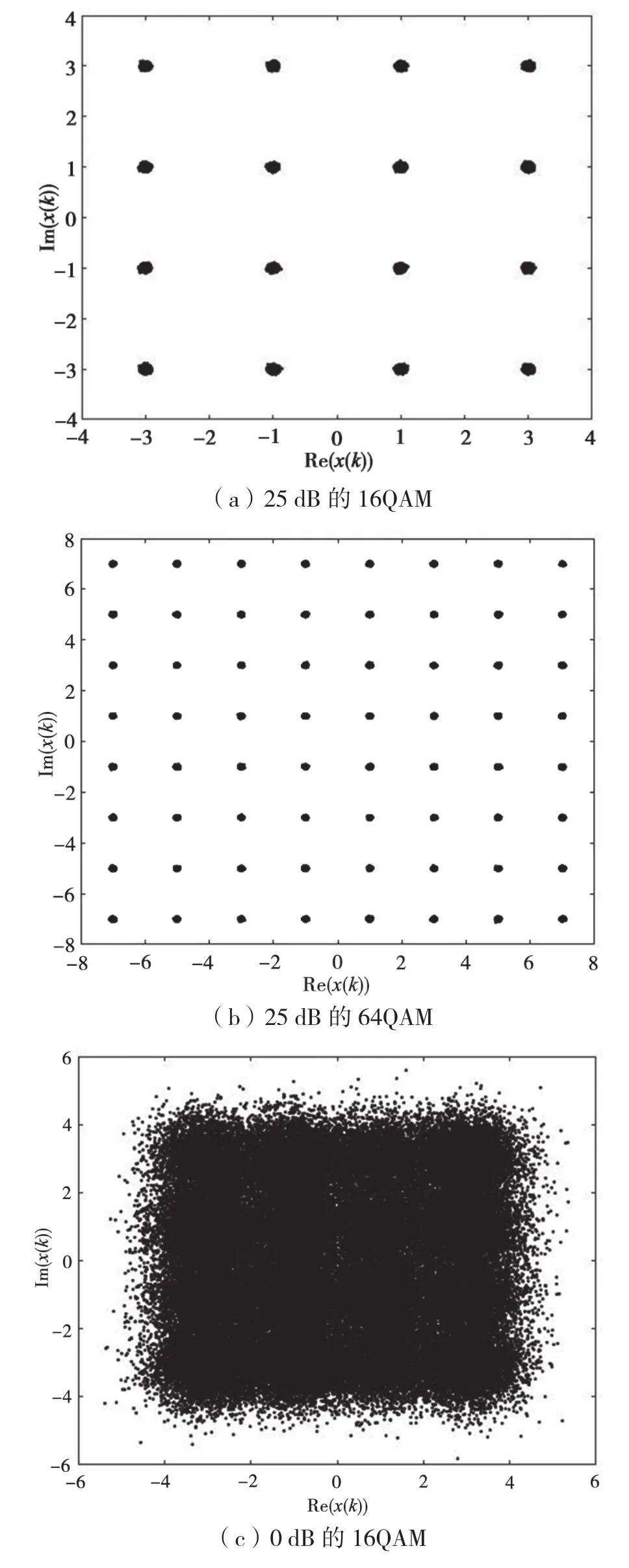
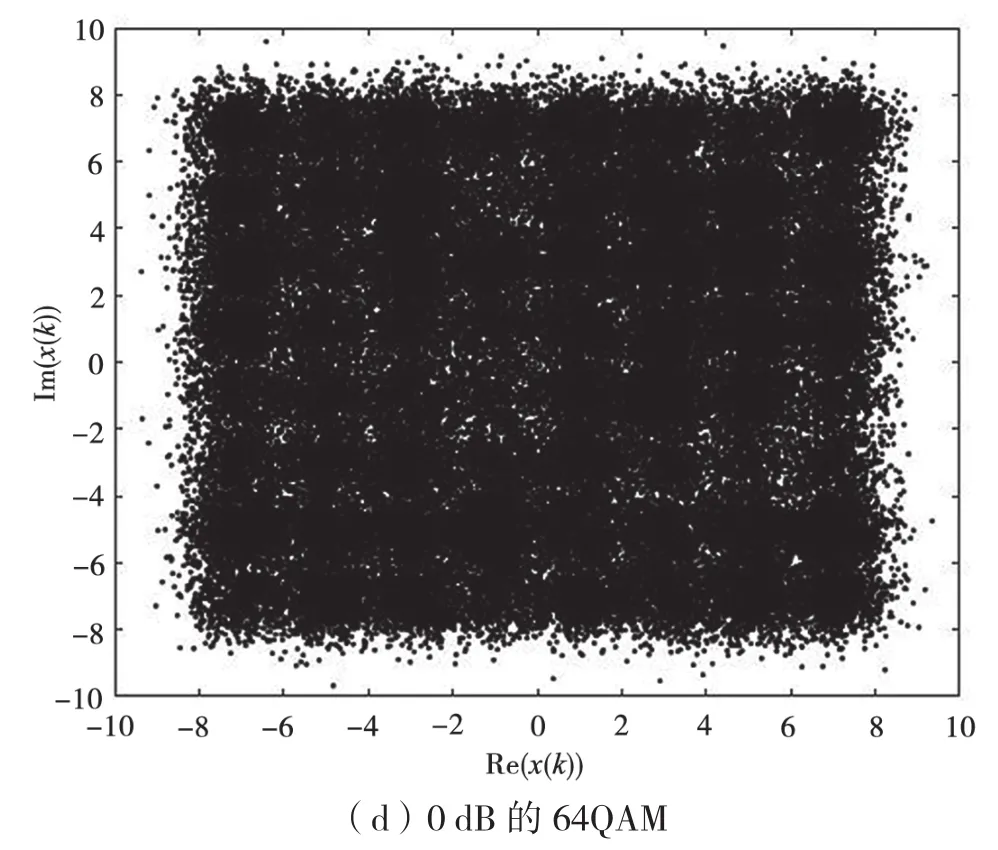
图1 几种信号的星座图

2 幅度相位分步识别算法

2.1 具体流程

如图2所示，本文先通过基本方法估计信号频率，然后还原带有频偏和相偏的基带信号；把带有频偏的星座图送入CNN识别，通过幅度信息进行第一次分类，之后通过减法聚类对相位信息进行二次分类，最后得到模式识别结果。

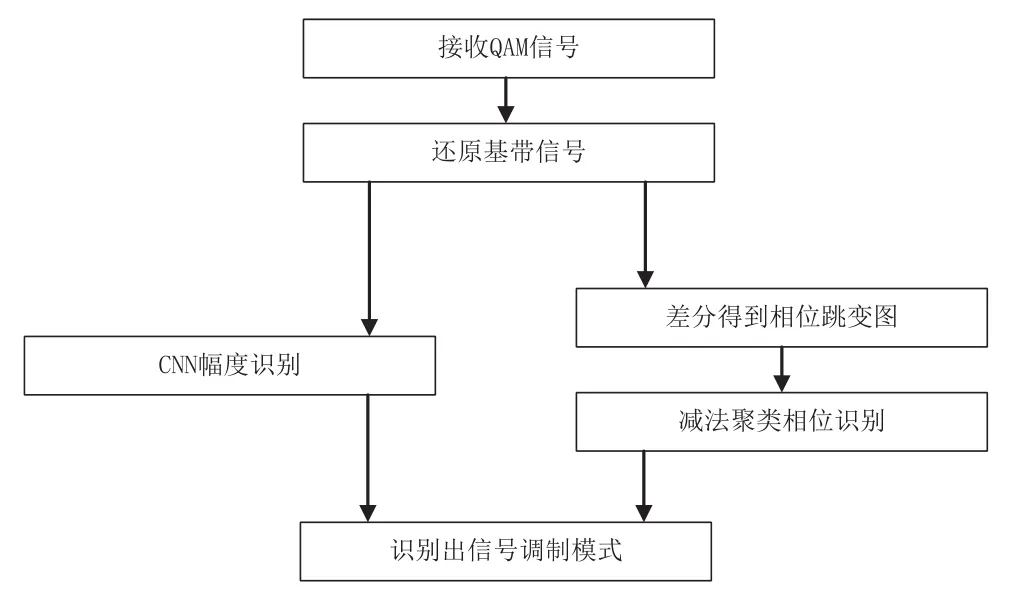
图2 幅度相位分步识别算法

2.2 CNN对幅度分类

星座图的频偏虽然会让星座图产生旋转，可是星座图中的幅度信息却被保留下来了。而PSK、16QAM和64QAM的幅度信息是有区别的，可以通过未消除频偏的星座图先把这几种信号区分开来。即通过未消除频偏的星座图，可以区分信号的幅度信息分为几层以及星座图中有几个圈。于是，搭建了如图3所示的卷积神经网络用于识别和分类。

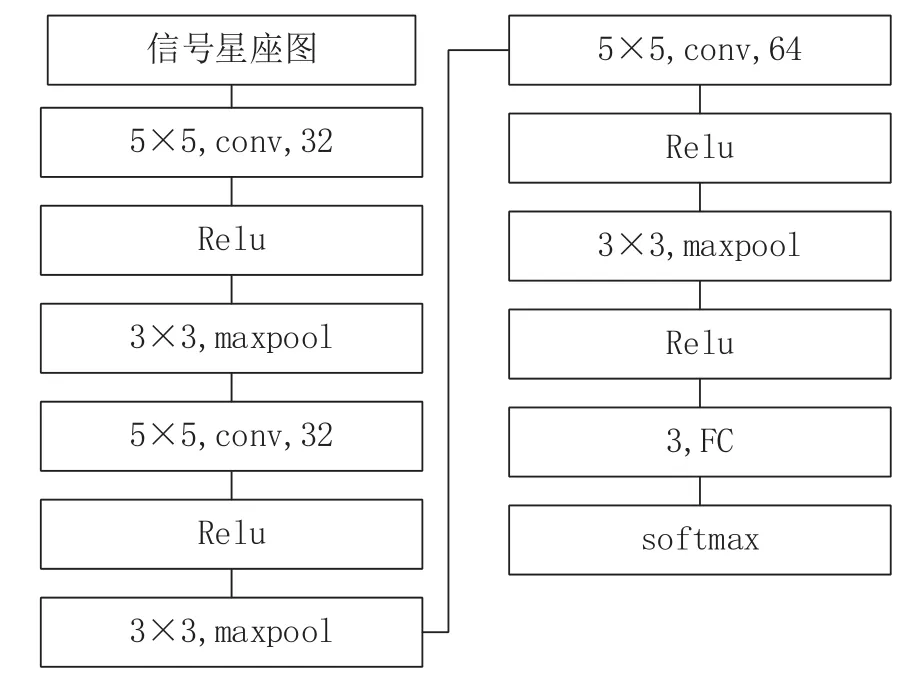
图3 卷积神经网络结构

因为未消除频偏，旋转的星座图更容易被CNN识别。图4是0 dB下未消除频偏的星座图和消除了频偏的星座图的16QAM和64QAM对比。

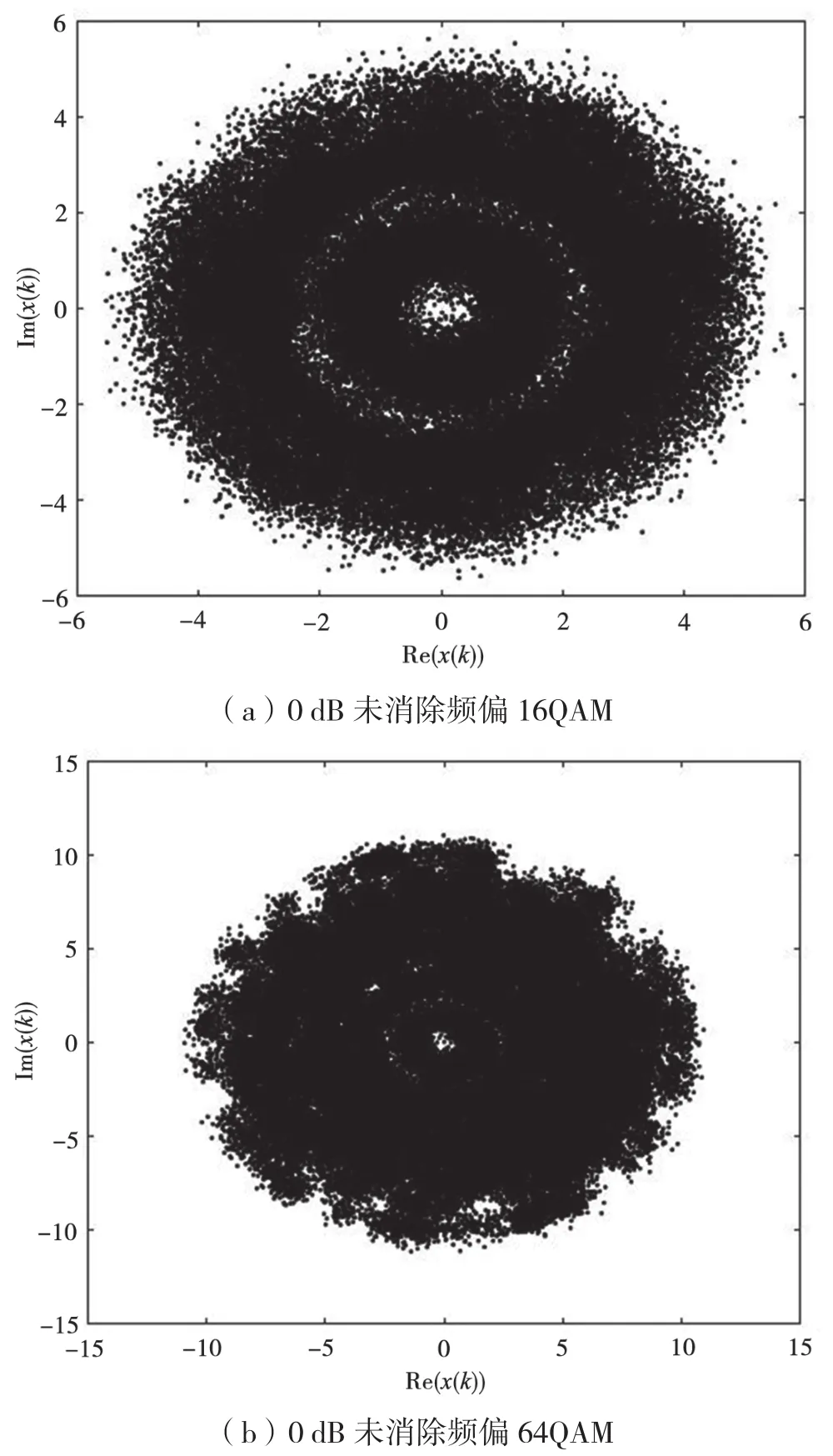
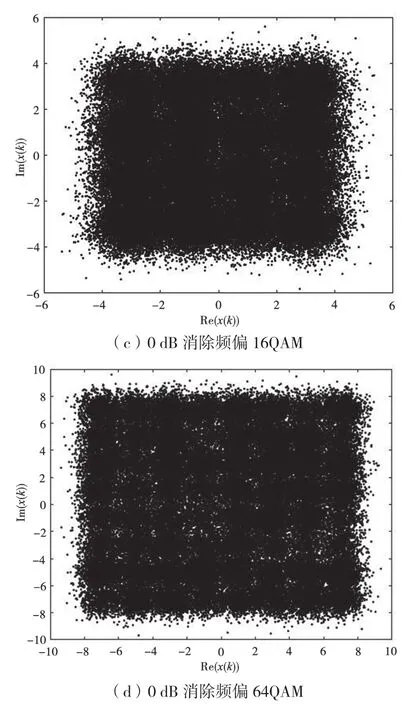
图4 未消除频偏和消除频偏的低信噪比星座图

从图4可以看出，对于未消除频偏的星座图，其在图像上的特征比消除了频偏的星座图更明显。在低信噪比下（0 dB），在本CNN网络中，未消除频偏的旋转类星座图比消除了频偏的星座图识别率略高，特别是针对点数过多的星座图，如16QAM和64QAM。

2.3 减法聚类对相位分类

相位分类部分采用了减法聚类的方法，这里从单层幅度信号即PSK信号讲解本文的相位分类方法。

首先，提取信号的瞬时相位φ(k)：

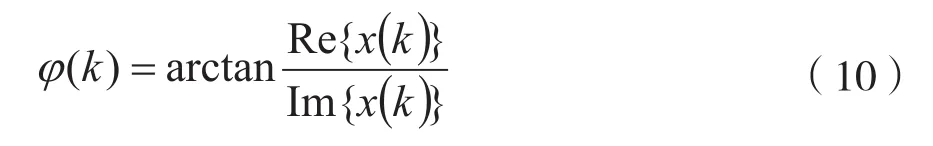
之后对相位进行差分，得到每个点之间的相偏：

对φ1作图，图5（a）是25 dB白噪声下的4PSK的相位差分图，横坐标为k，纵坐标为φ1。可以看出，相位差分后即使在有频偏和相偏的情况下，相位跳变信息也可以被很好地表现出来。将这些点合并到一个直线上，如图5（b）横坐标为两每个点的相位差，其被合并到了纵坐标为1的直线上。

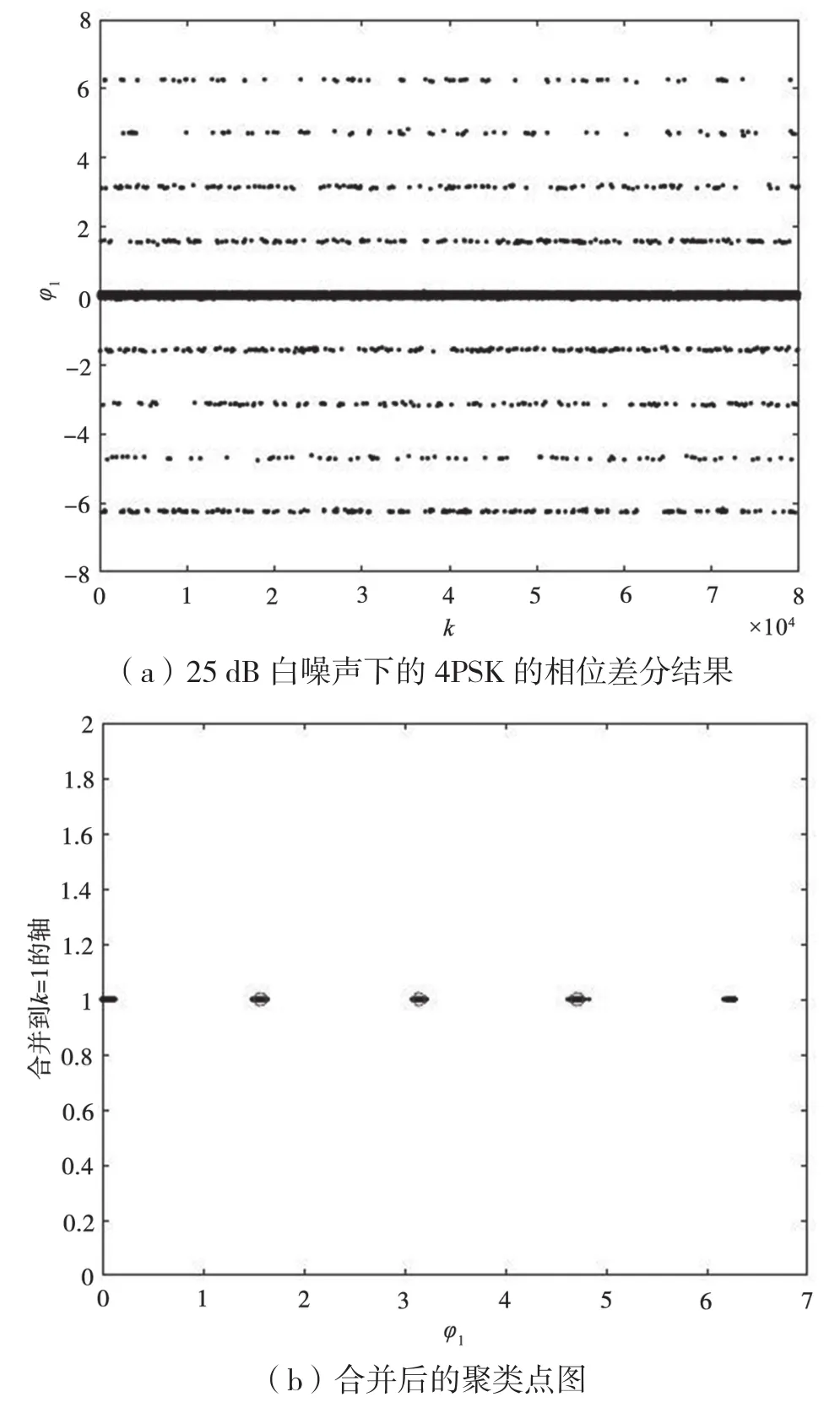
图5 相位差分后和减法聚类

最后，对这些合并后的点簇进行减法聚类。减法聚类算法假设每一个数据点都是聚类中心的候选者，并根据数据密度原理实现聚类分析[12]。该算法的具体实现如下，即设{x1,x2,…,xn}是d维空间中的聚类特征集，不失一般性，将特征集内所有特征点都归一化到一个超立方体内。定义特征点xi处的密度指标为：

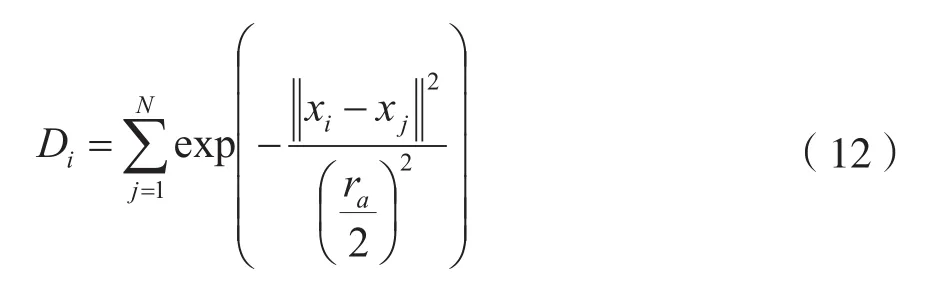
其中，N为总点数，半径ra是一个正数；定义了xi的一个邻域，半径以外的点对于xi的密度指标贡献很小。计算所有点的密度指标后，找出一个密度指标最大的点x1作为第一个聚类中心点，它的密度指标为D1，然后对剩下的点的密度指标进行修正：

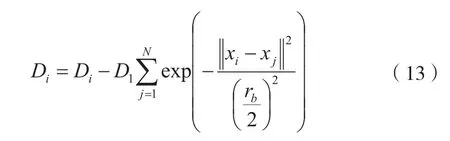
之后再次求取密度指标最大的点作为第二个聚类中心点，以此重复，直到达到设定的阈值ε，则停止聚类，详细算法参考文献[12]：

减法聚类后，可以区分出相位跳变聚为几类以及每一类的中心点位置。图5（b）为4PSK聚类结果。

3 实验结果与分析

3.1 星座图识别效果对比

用消除了频偏和相偏的星座图，像素为128×128的图片送入文中的神经网络训练，训练样本以高斯白噪声为噪声，信噪比为0～20 dB的PSK、16QAM、64QAM的3种调制信号，每种样本有1 000张图。之后用训练好的神经网络分别对各种0 dB调制信号的星座图进行识别，结果见表1。

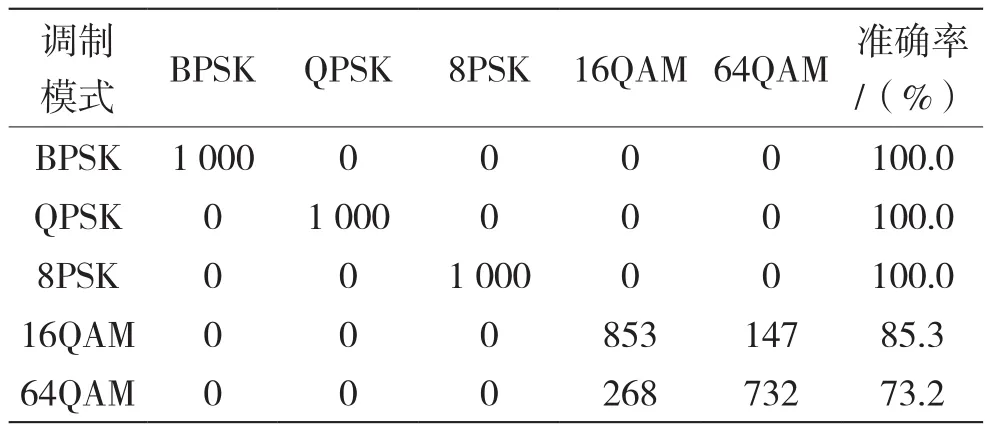
表1 消除了频偏的信号星座图识别的结果

用相同信号未消除频偏和相偏的星座图、像素为128×128的图片送入文中的神经网络训练，训练样本以高斯白噪声为噪声，信噪比为0～20 dB的PSK、16QAM、64QAM的3种调制信号，每种样本有1 000张图，之后用训练好的神经网络分别对各种0 dB调制信号的星座图进行识别，结果见表2。

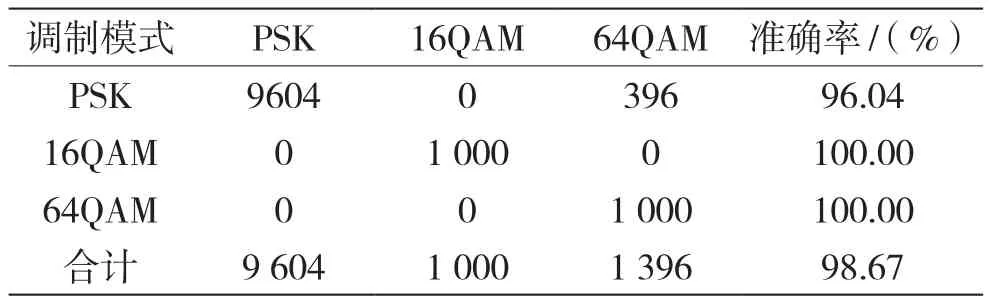
表2 未消除了频偏的信号星座图识别的结果

可以看出，本文提出的用未消除频偏的星座图送入神经网络识别的方法，比传统的消除频偏的星座图送入神经网络识别的方法，在0 dB信噪比下具有更好的识别率。

图6可以看出，未消除频偏的星座图在低信噪比下，在神经网络中的识别率比消除了频偏的星座图略好，特别是针对于高点数的星座图。

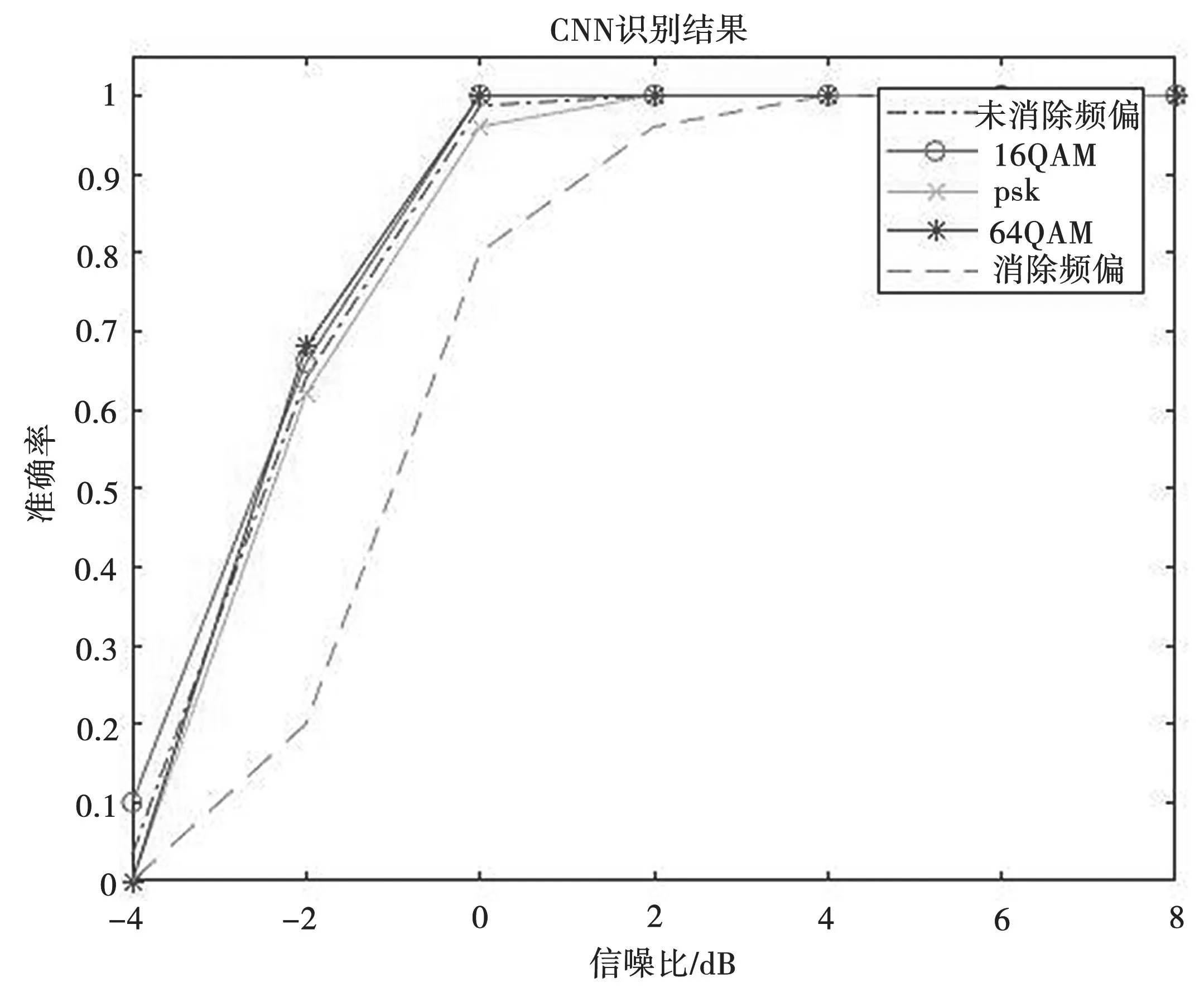
图6 未消除频偏星座图在不同信噪比下的识别率

3.2 减法聚类对PSK的分类效果

通过对CNN幅度信息的解读，把区别出来的PSK信号拿出来进行相位信息的分类。

文中的方法先对每点的角度进行差分处理，之后再对差分出来的序列进行减法聚类，通过聚类点数区分信号。表3为5 dB下的识别率。

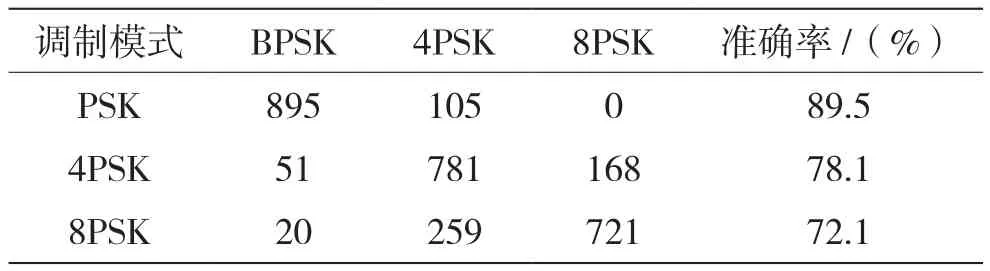
表3 减法聚类识别结果

通过文中所述的先进行相位差分再进行减法聚类的方法实现对于相位差分信息的分类，在低信噪比下并不令人满意，但这只是本文提出的一种对于后续相位信息的分类方法，由此来证明先通过幅度信息对信号进行分类，再通过相位差分信息对信号进行分类的识别方法达到抗频偏识别QAM、PSK等相位幅度为主的调制信号模式是可行的。通过CNN卷积神经网络识别幅度信息后，下一步对相位差分信息的分类是使用减法聚类更好还是其他方法更好，还有待于进一步讨论。

3.3 结合减法聚类的CNN识别QAM和PSK的结果

完整流程下，信号的识别结果如表4所示。

用设计的整个流程处理识别这些未分类的信号，神经网络很好地把PSK、16QAM和64QAM几种信号分离开，然后减法聚类对于相角差的分类也取到了一定作用，虽然效果没有神经网络好，但是可以说明，先通过神经网络对幅度信息进行划分，再对相位差信息进行识别来识别QAM类的信号的调制模式是可行的。

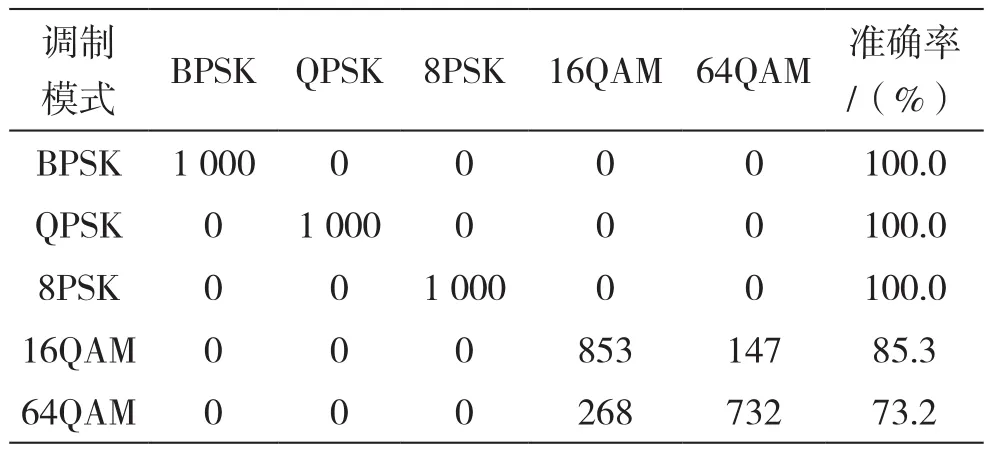
表4 总结果

4 结 语

实验发现，在本文的CNN网络中，在低信噪比情况下，对于未消除频偏的环状星座图的识别率是持平甚至略高于已经消除频偏的点阵星座图的，即依靠CNN来识别信号幅度信息不需要依赖于频偏或相偏消除的，且用传统简单的CNN就可以取得良好的效果。可见，先用CNN对信号的幅度信息作出一次分类，再利用差分和减法聚类对信号的相位差信息进行一次分类，由此识别几种QAM和PSK调制模式的方法是可行的。在低信噪比下，未消除频偏的星座图更容易被神经网络识别。这种方法能有效抵抗频偏和相偏，它的识别不会受到频偏和相偏的影响，在未消除频偏和相偏的信号调制识别或是频偏相偏消除不完全的信号调制识别中明显优于传统的使用CNN的识别方法。