双开缝矩形曲面网板水动力性能及影响参数研究

2020-03-26崔秀芳初文华王宏宇石福孝李培培

海洋渔业 2020年1期

陈刚，崔秀芳，初文华，王宏宇，石福孝，李培培

（1.上海海洋大学工程学院，上海 201306；2.上海海洋大学海洋科学学院，上海 201306；3.国家远洋渔业工程技术研究中心，上海 201306；4.大洋渔业资源可持续开发教育部重点实验室，上海 201306）

网板是单船拖网的重要属具，其水动力性能的优劣直接关系到拖网生产的渔获性能和经济效益。21世纪以来渔业迅速发展，而渔具装备越来越无法满足现代渔业的需求，其中网板的性能亦需进一步的优化。

迄今，国内外学者对网板水动力性能进行了较多的研究，YUKI等［1］通过不同间距和交错角度对双层网板周围的流场影响进行了研究；XU等［2-6］通过不同展弦比网板水动力性能和流态分布的影响进行了研究；王磊等［7-9］通过不同导流板对立式网板水动力性能影响进行了研究；刘健等［10-14］通过不同速度和多导流板对立式曲面网板水动力性能影响进行了研究；饶欣等［15-17］通过不同速度、曳纲和手纲连接点位置及展弦比对立式曲面V型网板受力影响进行了研究；庄鑫等［18-19］通过数值模拟的方法对网板周围流态进行了可视化研究；刘圣聪［20］通过数值模拟的方法对网板升阻比和稳定性进行了研究。然而上述学者主要是通过风洞和水槽实验法研究各种网板的水动力性能，并未考虑多种因素对其水动力性能的影响。

目前中国近海渔业普遍采用小型渔船作业，而迄今对于近海小型渔船所用的小型网板水动力性能的相关研究开展较少，且绝大多数通过风洞和水槽实验进行研究，成本高昂，不利于观察流态的变化；随着计算机的高速发展，数值模拟方法逐渐被应用各种场合，计算流体动力学（computational fluid dynamics，CFD）技术也被应用到网板性能优化中来，而数值模拟的方法则可以弥补风洞和水槽实验的不足。本文对一种双开缝矩形曲面网板的水动力性能进行了数值模拟，分析了冲角、速度、开缝尺寸和展弦比对网板水动力性能的影响，以期为网板结构优化设计提供参考。

1 材料与方法

1.1 数值模型

1.1.1 控制方程

本文假设各向同性、不可压缩的流体，控制目标方程包括连续性方程和N-S方程：

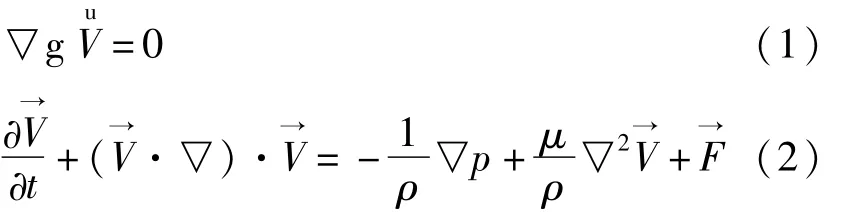
式（1）～（2）中：t为时间（s）；→V为流体速度（m·s-1）；F→为体积力（N）；p为压力（N）；μ为流体的动力粘度系数（kg·m-1·s-1）；ρ为密度（kg·m-3）。

1.1.2 参数定义

描述拖网网板水动力特性的参数主要有升阻比K、升力系数Cl、阻力系数Cd、雷诺数Re。计算公式如下：

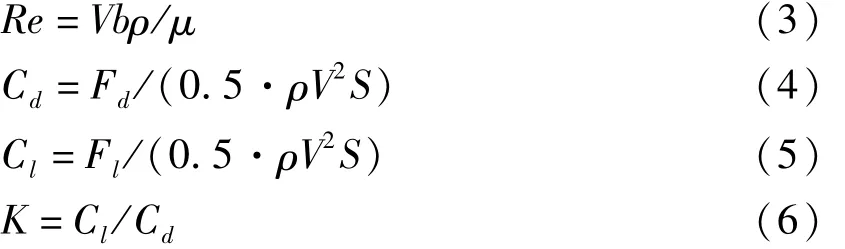
式（3）～（6）中：ρ为流体密度（kg·m-3）；b为网板弦长（m）；V为来流速度（m·s-1）；μ为流体动力粘度（kg·m-1·s-1）；Fd为网板阻力（N）；S为网板面积（m2）；Fl为网板扩张力（N）。

1.1.3 结构数值模型

本文所采用的计算模型为普通碳钢双开缝矩形曲面网板，该类型网板使用于底层拖网或中层拖网网具。翼弦长b=2 400 mm，翼展l=1 460 mm，开缝宽度d=50 mm；在此基础上，采用三维建模软件进行三维建模，模型如图1。

1.2 矩形网板水动力性能计算模型参数设置

由于网板结构复杂，在研究水动力性能时是非必要部件，本文对其结构进行适当简化，如包边、曳纲连接件、耳柄等对网板水动力性能没有影响，在计算时对其省略建模。

为计算网板结构水动力性能，本文采用计算流体力学软件对网板结构周围流场网格划分如图2-a所示，靠近网板的区域选择棱柱网格，远场区域选择四面体网格（即非结构网格）来进行计算。计算区域如图2-b所示，单元数约为1.1×107个，节点单元数约为2.6×106个。

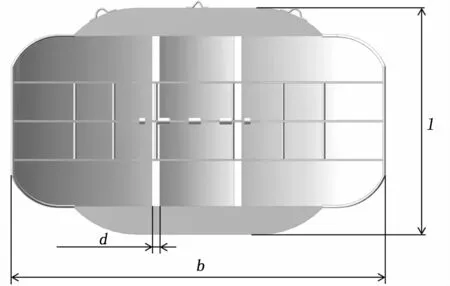
图1 网板结构模型Fig.1 Otter board structure model

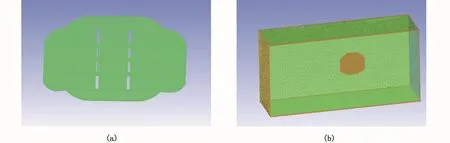
图2 数值模型Fig.2 Numerical model

选择计算流场模型选择RNGk-ε模型。上游入口处设定为速度入口边界（velocity inlet），方向沿X轴正向的均匀流，速度V=1 m·s-1，湍流强度设定为5%，湍流强度比设定为10，下游出口设定为完全发展自由出流边界（outflow），网板结构表面及计算域边界设定为不可滑移壁面（noslip wall）。

1.3 计算参数设置

为充分满足网板水动力性能在不同参数影响下所得仿真结果全面覆盖所有实际情况的可能性。因此，本文经过将模型简化后建立了如下4组对比计算模型：

（a）冲角是影响网板水动力性能的关键工作参数，为分析来流冲角α对该网板水动力性能的影响，在来流速度为1 m·s-1时，其他因素均相同的条件下网板迎流冲角α分别设置为：0°、5°、10°、15°、20°、30°、40°、50°、60°、70°进行仿真。

（b）在其他因素均相同的条件下分别设置来流速度V为：0.5、0.75、1、1.25、1.5、1.75、2、2.25、2.5、3 m·s-1进行仿真。

（c）本文所计算的矩形曲面网板为双开缝网板，为分析开缝尺寸大小对该网板水动力性能的影响，在来流速度为1 m·s-1、冲角为40°时，其他因素均相同的条件下网板开缝尺寸（水平投影宽度）分别取为：30、40、50、60 mm进行仿真。

（d）本文为分析展弦比大小对该网板水动力性能的影响，在来流速度为1 m·s-1、不同冲角，其他因素均相同的条件下网板展弦比分别取0.4、0.6、0.8、1.0、1.2进行仿真。

2 结果与分析

2.1 冲角对网板水动力性能的影响

图3给出了在来流速度为1m·s-1时矩形曲面网板阻力系数Cd、升力系数Cl及升阻比K随冲角的变化情况。

图3显示，随冲角的增加，网板的升力系数呈先增后减的趋势，在40°左右达到最大值；而阻力系数则在70°范围内随冲角的增加持续增大，二者同时的作用下，随冲角的增加，网板的升阻比同样呈现先增大后减小的趋势，但最大升阻比出现在冲角为10°左右。

图4给出了网板在不同冲角下的流场速度矢量图，从图4中可看出，随着冲角α的增加，网板迎流面与背流面速度差异逐渐增大，由流体动力学理论可知，网板的升力系数也将随着冲角的增加而逐渐增大。但在冲角增大到30°左右时，网板背流面开始出现明显的边界层分离，且在靠近尾部的区域出现较为明显的漩涡，当冲角增加到50°时，网板背部的漩涡已十分明显，这一漩涡的出现会导致网板升力系数的显著下降。

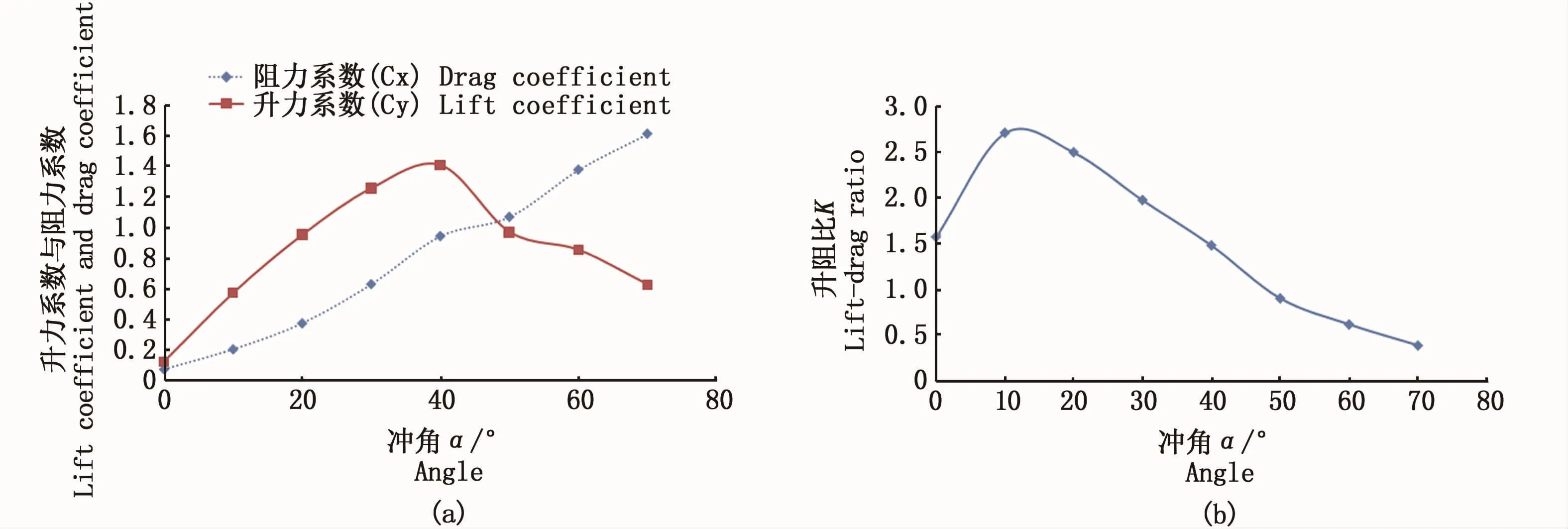
图3 网板升力系数、阻力系数及升阻比随冲角的变化规律Fig.3 Variations of lift coefficient，drag coefficient and lift-drag ratio of otter board

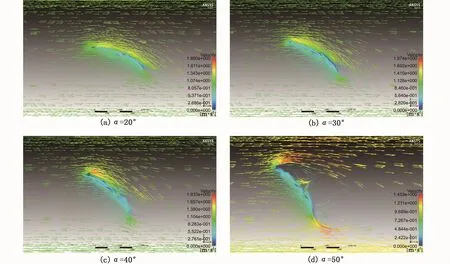
图4 网板不同冲角下周围流场速度分布图Fig.4 Flow velocity distribution around the otter board at different angles of attack

2.2 速度对网板水动力性能的影响

由式（4）和式（5）可以推断出，阻力系数和升力系数与速度无关，为验证推断，图5给出了矩形曲面网板在不同冲角下的升力系数随速度变化的规律。可以看出，在同一冲角下，矩形曲面网板的升力系数随速度的增加无明显变化趋势。

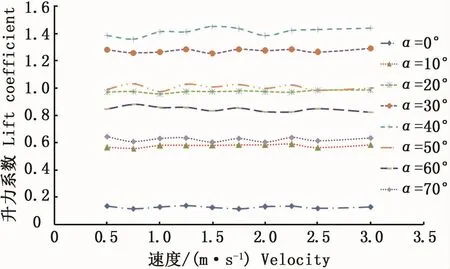
图5 不同冲角下矩形曲面网板升力系数随速度变化规律Fig.5 Variations of lift coefficient of rectangular mesh plate with velocity under different angles of attack

2.3 开缝尺寸对网板水动力性能的影响

图6 给出了网板在来流速度为1 m·s-1、冲角为40°时升力系数及升阻比K随开缝尺寸的变化情况。

结果显示，开缝尺寸对于矩形曲面网板的水动力性能有较为明显的影响。升力系数随开缝尺寸的增加总体呈增大的趋势，当开缝尺寸大于50 mm时，升力系数无显著变化；而升阻比随开缝尺寸的增加呈先增加后减小的趋势，在开缝尺寸达到60 mm左右时，升阻比达到最高值。

2.4 展弦比对网板水动力性能的影响

本文为分析展弦比大小对该网板水动力性能的影响，将展弦比分别设置为0.4、0.6、0.8、1.0、1.2，计算其在来流速度为1 m·s-1、不同冲角的水动力性能。图7给出了网板升力系数Cl、阻力系数Cd及升阻比K随开缝尺寸的变化情况。

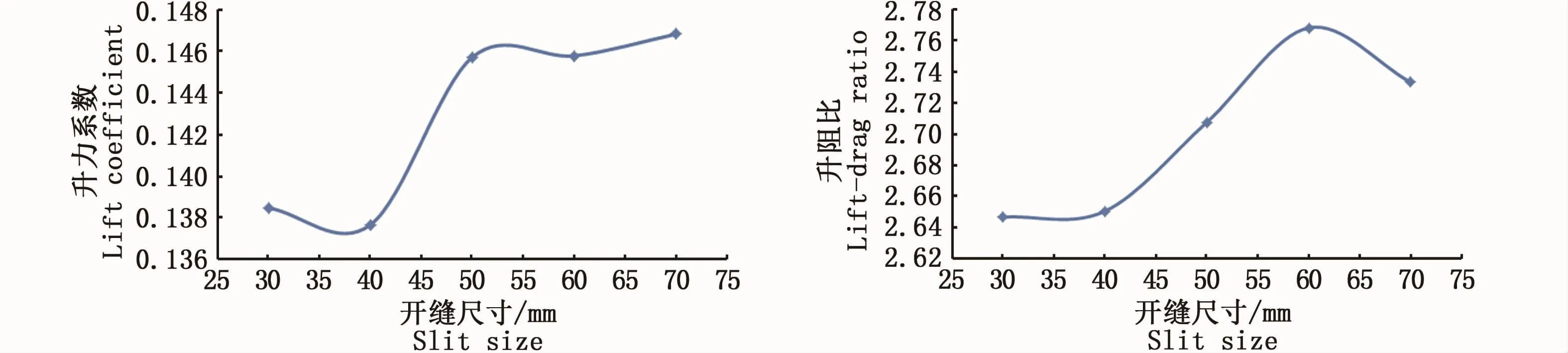
图6 矩形曲面网板开缝尺寸对水动力性能的影响Fig.6 Effect of slit size of rectangular curved mesh plate on hydrodynamic performance

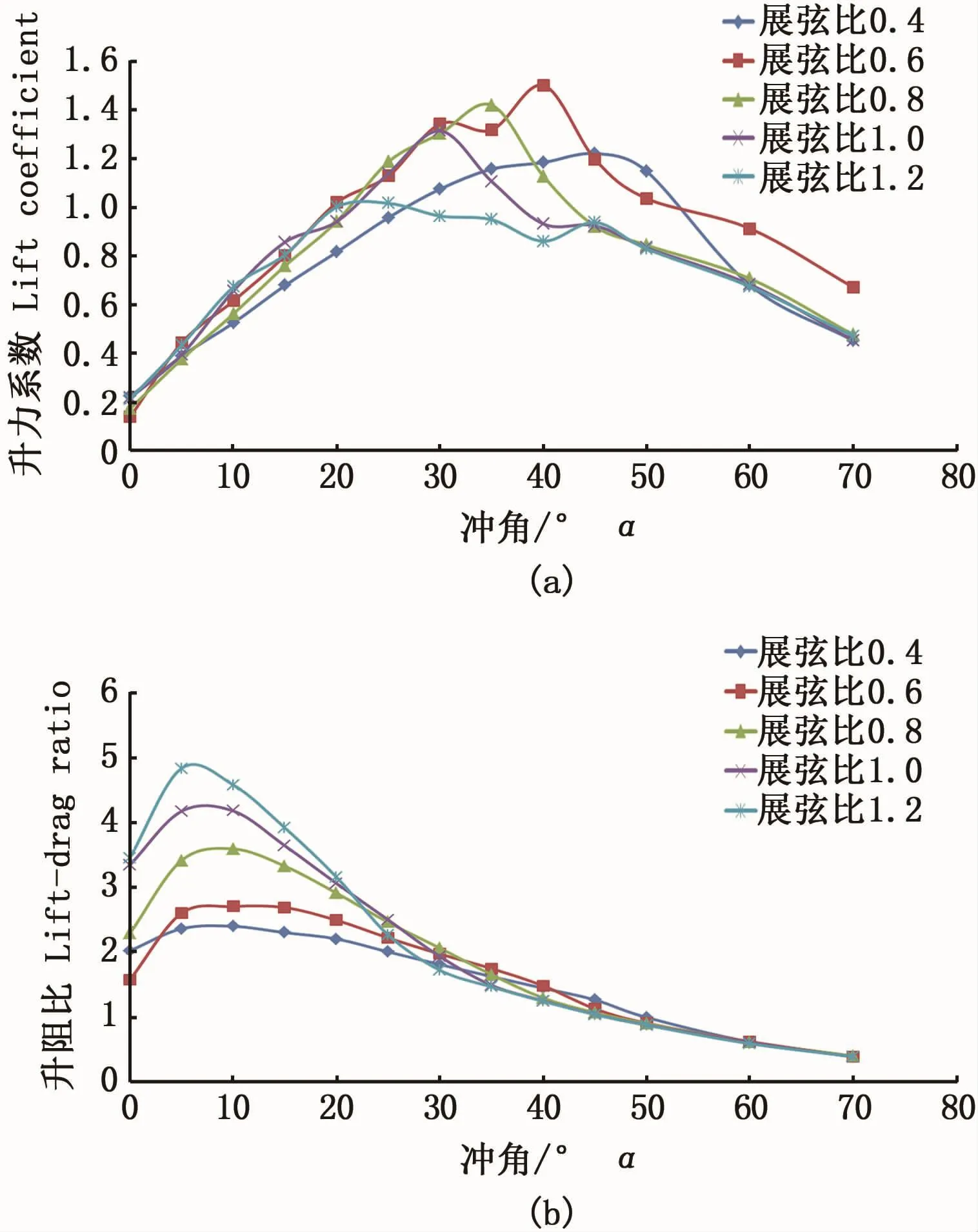
图7 矩形曲面网板展弦比对水动力性能的影响Fig.7 Influence of the aspect ratio of rectangular curved otter board on hydrodynamic performance

从图7可以看出，矩形曲面网板的水动力性能受展弦比的影响十分显著。对于网板的扩张效果方面来说，从图7-a中可以看出，不同展弦比的网板在升力系数达到最大时对应的最佳冲角随展弦比的增加而逐渐减小。同时，升力系数峰值随展弦比的增加呈先增后减的趋势，当展弦比为0.6左右时，升力系数的峰值达到最大；在30°冲角范围内，展弦比小于0.6时，升力系数随展弦比的增加而显著增加，当展弦比大于0.6时，升力系数随展弦比的增加无显著变化。从升阻比角度考察不同展弦比网板的总体性能可以看出（如图7-b所示），在一定范围内，矩形曲面网板的升阻比随展弦比的增加而增大。