超声导波用于液层负载板损伤检测的数值模拟

陈维业，吴先梅，刘 松，陈家熠

(1. 中国科学院声学研究所声场声信息国家重点实验室，北京100190；2. 中国科学院大学，北京100049)

0 引 言

伴随着海洋资源的不断开发利用及海洋战略的需求，液层负载薄板结构越来越多地应用到海洋钻井平台、大直径管道及舰艇等海工装备[1-2]。但受外界环境和自身结构等因素影响，结构表面和内部难免会产生腐蚀、裂纹等损伤缺陷，缺陷的累积会严重影响其安全性，因此这些装备的损伤检测和健康监测也成为了一个关键问题。

超声导波具有在介质中传播距离长、可实现高效在线监测等优势，在板结构的损伤检测方面得到了广泛的关注[3]。马伟伟[4]采用分段计算的方法来分析Lamb 波在缺陷板中的传播，并通过理论和数值模拟研究单层板中裂纹深度与损伤指数的关系。张超[5]对不同类型分层板的激发特性等进行了系统的分析，为分层板结构的损伤检测提供依据。而Lamb波在传播过程中会发生频散，影响损伤的定位和成像，利用时间反转方法能够补偿Lamb 波的频散[6-7]。何存富等[8]采用多通道时间反转方法对板中Lamb波进行聚焦，实现板内缺陷的准确定位并提高小缺陷识别分辨能力。但应用超声导波对含损伤液层负载薄板结构的研究相对较少。因此，本文通过计算4 mm 厚双侧水域负载铝板的频散曲线来选择合适的激励频率和激励方式。同时利用有限元模拟研究了所选激励条件下双侧液体负载铝板中不同位置、角度及大小的缺陷对检测信号的影响。

1 双侧液体负载薄板中的漏Lamb 波

1.1 模型的建立

针对于单层板中的声传播特性及损伤检测，国内外学者已开展了广泛的研究，本文所建立的是如图1 所示的双侧液体负载薄板模型，图中x 方向为声传播方向，z 方向为板厚方向，中间固体板的厚度为2h，两侧为半无限大液体。

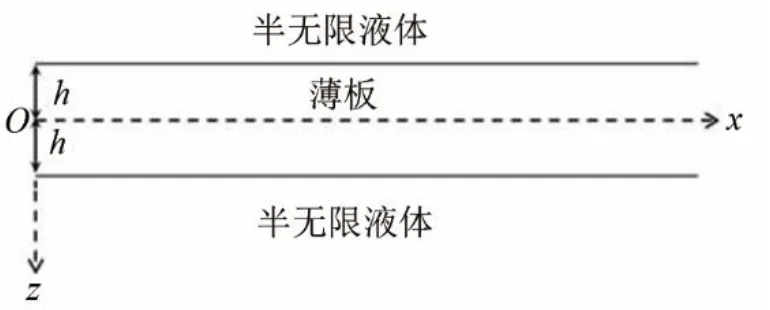
图1 双面液体负载薄板几何示意图Fig.1 Geometry model of double-sided liquid layer loaded thin-plate

1.2 特征方程的求解

Lamb 波是在自由板中产生的平面应变波，在板的上、下表面应力为零，随着波的入射角和频率的改变，在每一个点上都产生不同的模态结构[9]。而对处于一定振动模式的液体负载板，板中的声能量会向液体中辐射，从而形成漏Lamb 波。当板的两侧负载为半无限大理想液体时，薄板中类Lamb波对称模式(S 模式)的频散方程为[10]

反对称模式(A 模式)的频散方程为[10]

其中：

式中：CL为固体材料中纵波速度；CT为固体材料中横波速度；ρL为液体的密度；ρS为薄板的密度；f为激励频率；k 为实波数；γ为虚波数，即衰减因子。

铝板及水的相关参数如表1 所示。将参数代入

表1 双面液体负载板模型参数[5,11]Table 1 Model parameters of double-sided liquid layer loaded thin-plate [5,11]

图2 4 mm 双侧液体负载铝板频散曲线Fig.2 Dispersion curves of double-sided liquid layer loaded 4 mm aluminum plate

式(1)、(2)可以计算得到如图 2(a)～2(c)所示的4 mm 双侧半无限大水域负载铝板的相速度曲线，群速度曲线和衰减曲线。

1.3 激励频率与激励方式的选取

在液层负载条件下，激励频率的选择主要考虑两个方面，即声波的频散小和衰减小。群速度的变化率小对应声波的频散小，衰减因子的值小对应声波的衰减小。由图2(b)、图2(c)可见，激励频率为100 kHz 以内的S0 模式能够很好地满足上述两个方面的要求，本文选用的激励频率为80 kHz。在激励频率为80 kHz 时，为获得单一的S0 模式，本文选用双面法向激励的方式。

2 双侧液体负载损伤薄板的数值模拟

2.1 有限元模型的建立

应用有限元软件对含缺陷的双侧水域负载铝板进行模拟，其模型坐标如图3 所示。坐标原点O 位于铝板左端面和板厚方向中间面的交点，铝板的长度为 2 000 mm，厚度为 4 mm，水域的高度为200 mm，设置铝板及水域的吸收边界条件来模拟无限大铝板和半无限大水域。缺陷的长度为l，宽度为w，其左端面的横坐标为1 000 mm。缺陷高度方向中心到薄板中间面的距离为d，定义为缺陷位置深度。激励源位于铝板的上下表面来实现双侧法向激励，为获取足够能量的信号，线源长度取10 mm，其中心点横坐标为405 mm。有限元模拟时采用5个周期的汉宁(Hanning)窗调制的正弦波作为激励信号，信号的中心频率f=80 kHz，其时域波形如图4 所示。另外A、B、C、D 四点位于铝板的上表面，其x 方向坐标分别为600、700、1 300 和1 400 mm，用来接收信号。

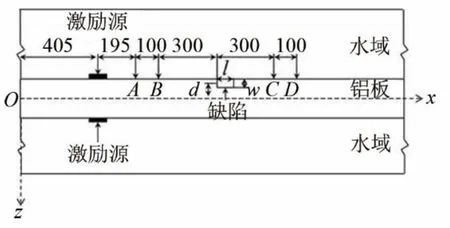
图3 含缺陷双侧水域负载铝板模型1 的坐标图Fig.3 Coordinate chart of Model 1 of the water loaded aluminum plate with defects

2.2 模拟结果分析

2.2.1 缺陷位置深度对接收信号的影响

图4 激励源信号时域图Fig.4 Time domain diagram of excitation source signal

通过分析缺陷的反射信号和透射信号可以获得损伤缺陷的相关信息，其中无缺陷双侧水域负载铝板x 方向坐标为600 mm、1300 mm 即位置A、位置C 处的法向振动位移波形如图5 所示。

图5 无缺陷双侧水域负载铝板位置A、C处法向振动位移波形图Fig.5 Normal vibration displacement waveforms at the positions A and C of the water loaded non-defective aluminum plate

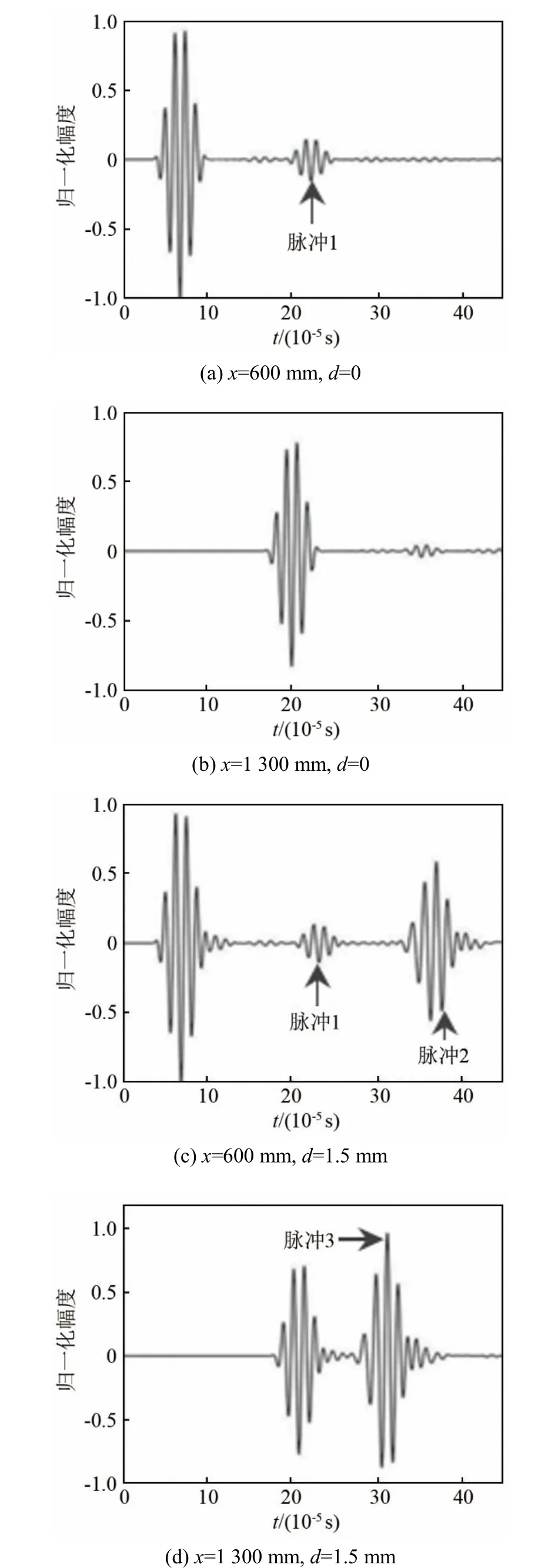
图6 含 l=5 mm，w=1 mm缺陷时，位置A、位置C法向处的振动位移波形图Fig.6 Normal vibration displacement waveforms at the positions A and C of the water loaded aluminum plate with the internal and surface defects of l = 5 mm and w = 1 mm

图6 所示为存在内部缺陷或表面缺陷的双侧水域负载铝板在位置A、位置C 处的法向振动位移波形，缺陷的长度l、宽度w 分别保持5 mm 和1 mm，缺陷位置深度d 分别为0 和1.5 mm，分别对应缺陷中间面与铝板中间面重合、缺陷位于铝板表面。对比图5(a)和图6(a)可见，图6(a)中幅值较小的脉冲1为缺陷反射回波，通过获取位置B 的信号，计算当脉冲 1 传播距离为 0.1 m 时，传播时间为1.87×10-5s，则其相速度为5 348 m·s-1，与图2(a)对比，可知其模式为S0 模式。对比图6(a)、6(c)，可以发现当缺陷位于铝板表面时，出现了一个新的声脉冲，即图6(c)中的脉冲2，此声脉冲到达时间明显晚于脉冲1。对比图6(b)、6(d)，图6(d)中同样出现了新脉冲，即脉冲3。通过获取位置B 和位置D 的接收信号来计算脉冲2 和脉冲3 的相速度，可得脉冲2 和脉冲3 为A0 模式信号。可见当缺陷位于铝板表面时发生了明显的模式转换，并且A0 模式信号的幅值大于S0 模式信号的幅值。为探究发生模式转换的影响因素，在铝板的上下表面设置l=5 mm，w=1 mm 的对称缺陷进行数值模拟，位置A 和位置C 处所接收的信号如图7 所示。对比图7(a)、图6(c)或图7(b)、图6(d)可见，当缺陷关于板厚方向对称时，未观察到明显的模式转换现象。因此可以判定，当缺陷的存在造成结构的不对称性时会使得S0 模式的信号转换出明显的A0 模式信号。这是因为对称模式S0 不能单独满足不对称边界条件，从而使得部分能量转换生成反对称模式A0。

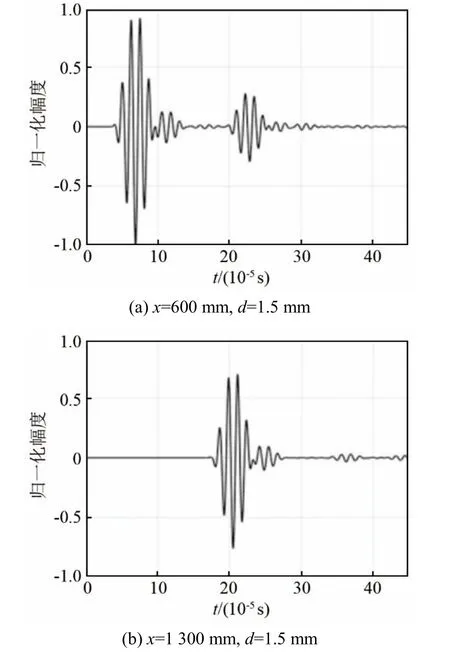
图7 含l=5 mm，w=1 mm 对称缺陷时，位置A、位置C法向振动位移波形图Fig.7 Normal vibration displacement waveforms at the positions A and C of the water loaded aluminum plate with the defects of l = 5 mm and w = 1 mm symmetrically on the upper and lower surfaces

通过分析数值模拟结果发现，随缺陷位置深度变化，S0 模式信号幅值变化不明显，A0 模式信号幅值变化较为明显。因此，本文分析A0 模式的透射系数与缺陷位置深度的关系，其中透射系数指A0模式透射信号与激励源处信号能量的比。以信号包络的平方对时间的积分来描述信号的能量：

缺陷长度l 为5 mm、宽度w 为1 mm 时，单层铝板和水域负载铝板在位置C 处透射系数随缺陷位置深度的变化如图8 所示。由图8 可见，随着缺陷位置深度的减小，即d 值的增大，A0 模式信号的透射系数单调递增。

为研究缺陷方向对接收信号的影响，双侧水域负载损伤铝板模型坐标图如图9 所示。缺陷与铝板中间面的夹角为α，缺陷的最左端与铝板左端的距离为1 000 mm。缺陷的长度l 为5 mm，宽度w 为1 mm，其对称中心位于铝板的中间面。A、B、C、D 点的位置及线源的位置、长度，激励方式、激励信号等设置与图3 相同。

图8 A0 模式透射系数与缺陷位置深度的关系Fig.8 Relationship between the transmission coefficient of A0 mode and the depth of defect position

图9 含缺陷双侧水域负载铝板模型2 的坐标图Fig.9 Coordinate chart of Model 2 of the water loaded aluminum plate with defects

2.2.2 缺陷方向对接收信号的影响

图10为4 mm厚双侧水域负载铝板及单层铝板在位置C 处A0 模式透射系数与缺陷角度关系图。由图10 可见，随着缺陷角度α 由0°增加到35°，透射系数先增大后减小，液层负载铝板的转折点发生在25°左右，单层铝板的转折点发生在30°左右。

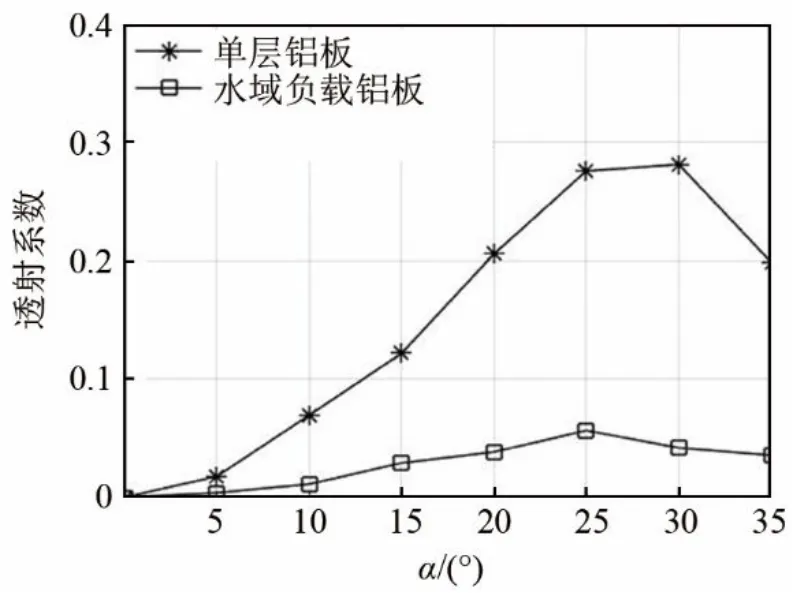
图10 A0 模式透射系数与缺陷角度的关系Fig.10 Relationship between transmission coefficient of A0 mode and defect angle

2.2.3 缺陷大小对接收信号的影响

图11 所示是缺陷位置深度d 为0.75 mm 和1.5 mm，即缺陷分别位于铝板的内部和表面，缺陷宽度w 保持1 mm，角度α 保持为0°的条件下，位置C 处的A0 模式透射系数随缺陷长度的变化曲线图。

由图11 可见，在计算范围内，随缺陷长度的增加，A0 模式信号的透射系数均呈先增大后减小又增大的趋势，这是因为缺陷的存在使板的厚度发生两次变化，引起S0 模式信号发生两次模式转换而生成两个A0 模式信号，两个A0 模式信号叠加成一个波包。随着缺陷长度的改变，生成的两个A0 模式信号相位差发生改变，即叠加状态发生改变，从而引起计算范围内透射系数随缺陷长度的增加呈先增大后减小又增大的变化趋势。

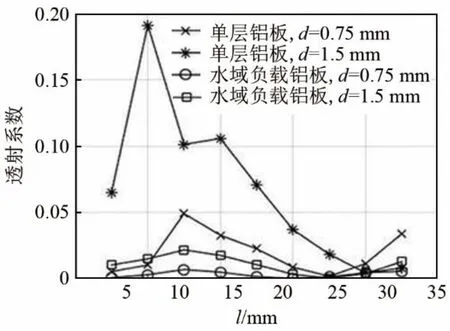
图11 A0 模式透射系数与缺陷长度的关系Fig.11 Relationship between transmission coefficient of A0 mode and defect length

另外，本文计算了缺陷位于表面时缺陷宽度w与A0 模式透射信号的关系，来模拟实际工况下腐蚀深度对检测信号的影响。保持缺陷长度l 为5 mm，缺陷角度α 为0°，位置C 处A0 模式透射系数与缺陷宽度w 的关系如图12 所示。由图12 可见，随着缺陷宽度由0.5 mm 增加到2.5 mm，A0 模式透射系数逐渐增大，这是因为缺陷宽度的增大造成了铝板不对称程度的增大，增强了模式转换效应。

图12 A0 模式透射系数与缺陷宽度的关系Fig.12 Relationship between transmission coefficient of A0 mode and defect width

由于边界条件的改变及声波衰减的影响，以上三种情况下水域负载铝板的透射系数均小于单层铝板的透射系数。另外本文通过数值模拟定性分析了缺陷位置、角度及大小对检测信号的影响，定量分析及实验条件下三种情况对检测信号的影响还有待进一步的研究。

3 结束语

本文通过求解双侧液层负载薄板的频散方程，计算得到4 mm 双侧水域负载铝板的频散曲线。利用有限元模拟对含不同位置、角度及大小缺陷的双侧水域负载铝板进行了仿真计算，并定性分析了缺陷位置、角度及大小对板内声信号的影响。研究结果表明：对于4 mm 厚双侧水域负载铝板，中心频率为100 kHz 以内的S0 模式漏Lamb 波衰减因子趋近于零，适合长距离损伤检测。另外，以频率为80 kHz 的S0 模式漏Lamb 波作为检测信号时，当缺陷的存在造成板结构的不对称性时，波形在缺陷处会发生明显的模式转换，并且S0 模式转换出的A0 模式信号的透射系数能够较好地反映缺陷位置、角度及大小的变化。A0 模式的透射系数随缺陷位置到板厚中心距离的增加而增大，随缺陷角度的增加先增大后减小，随缺陷长度的增加呈先增大后减小又增大的变化趋势，并随缺陷宽度的增大而增大。本文的研究结果能够为液层负载板结构的损伤检测和健康监测提供依据。