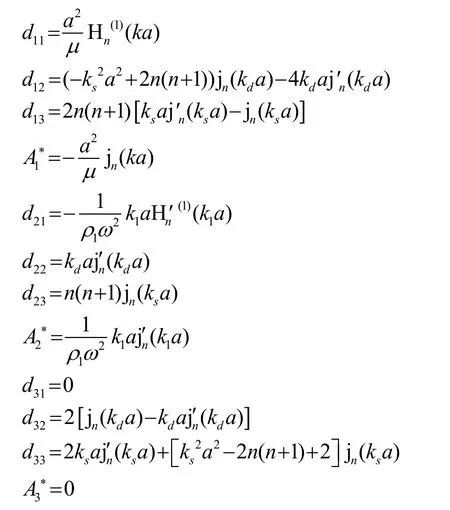基于声学隧道效应的低频目标强度增强技术

徐盛瀛，范 军，王 斌

(上海交通大学高新船舶与深海开发装备协同创新中心，海洋工程国家重点实验室，上海200240)

0 引 言

作为主动声呐方程中的重要参数，目标强度(Target Strength, TS)是表征目标对声波散射能力的物理量[1]。随着海洋资源开发利用的迅速发展，人们对水下高目标强度标记物的需求日益增加，例如沉船打捞、管线定位以及网箱标记等。通常情况下，目标强度随着标记物尺度的减小呈现下降趋势。另一方面，主动声呐工作频率呈现低频化发展趋势，尤其是深远海开发的国家战略背景下。因而，研究如何提高小尺度标记物的低频目标强度具有重要意义。

角反射体[2]由于在特定的空间方位角具有较高的目标强度或较大的散射截面，已经被广泛应用于雷达电磁波反射的标定。然而，角反射体在水下声波反射标记中的应用却受到了严重的限制，主要原因是在低频情况下，水中角反射体各反射面的透射系数较大，角反射增强效果下降；除此之外，洋流作用下的角反射体姿态难以控制，会导致回波幅度起伏剧烈。

除了角反射体以外，Malme 在研究水中气泡声散射过程中发现，充气圆柱散射体在低频时可以获得较高的目标强度[3]，但是尺寸较大、制作困难，且在水压作用下很难保持形状，因此实际应用并不广泛。

Hefner 等[4]在对高分子聚合物(polymethyl methacrylate, PMMA)声散射特性理论研究时发现，PMMA 材料中的Rayleigh 波波速比水中声速要低，因此在低频段内会发生Rayleigh 波共振现象，Hefner 称其为声学隧道效应(acoustic tunneling effect)，从而使PMMA 材料目标在低频时可以获得较高的目标强度，这为低频目标强度增强技术提供了一种新的思路。

本文以文献[4]的研究为基础，对相同尺寸的钢球和PMMA 球的目标强度进行了理论和试验分析。首先在弹性球简正级数解的基础上，计算了相同尺寸的钢球和PMMA 球的目标强度，发现在低频段(ka＜6)内的相同尺度的PMMA 球目标强度大于钢球目标强度。采用Regge 轨迹跟踪法计算了弹性球表面波相速度的频散曲线，计算表明钢球中Rayleigh 波相速度高于水中声速，是一类超音速波，PMMA 球中Rayleigh 波相速度低于水中声速，是一类亚音速波。采用亚音速波声学隧道效应和表面环绕波传播共振特性，对PMMA球中亚音速Rayleigh 波形成的低频目标强度增强进行了物理机理解释和分析。最后，进行了PMMA球和钢球目标强度测量对比试验，验证了理论分析结果，为实现低频目标强度的增强提供了一种新思路和新方法。

1 弹性球散射声场简正级数解

假设单位幅度平面波沿着z 轴入射，将其进行球面波分解(忽略时间因子e− iωt)[5]，可得：

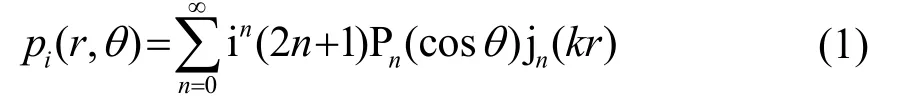
其中：jn(k r )是球贝塞尔函数，Pn(cosθ )是勒让德函数；k 为声波波数。

对于半径为a、球心与坐标原点重合的弹性球，其散射波声场可以表示为

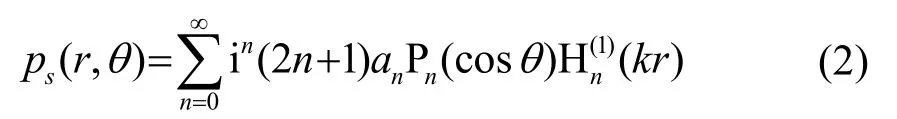
根据亥姆霍兹(Helmholtz)定理，弹性球体位移可以表示为

其中：(0,Ψ ,0)表示该向量势中θ 分量与r 分量恒等于0；Φ 和Ψ 分别为纵波、剪切波位移势函数，通

解形式为

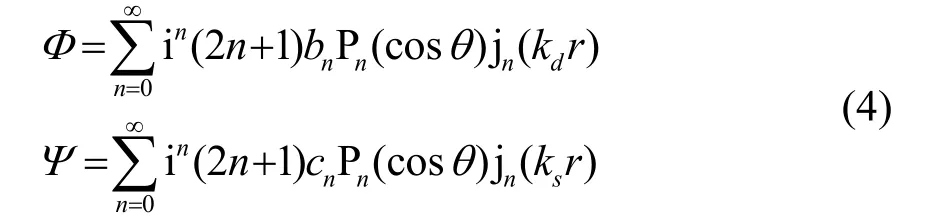
其中：kd、ks分别为纵波波数、横波波数；bn、cn是待定系数。

根据弹性球表面的法向应力、位移连续以及切向应力为0 的条件，即

根据式(5)以及球坐标系下应力、应变关系，可以得到关于系数an、bn、cn的方程组

式(6)中各元素见附录。根据式(6)可以求得an，进而计算弹性球目标强度：

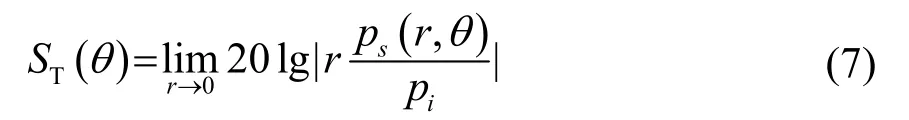
收发合置情况下，θ=π。

2 PMMA 球散射特性与机理分析

根据式(7)计算PMMA 球、钢球目标强度随频率变化的规律。钢球的材料损耗对其低频散射声场的影响可以忽略，即忽略材料对声波的吸收。然而，PMMA 材料及其他高分子聚合材料对声波的吸收作用是不可忽略的，为此，在计算PMMA 球目标强度时，需要引入一个复波速[6-7]来表示这种吸收作用。计算参数选取如表1 所示。

表1 计算参数选取Table 1 Calculation parameters selection

图1 给出了半径均为55 mm 的钢球和PMMA球目标强度随频率变化的规律，横坐标为归一化频率ka，纵坐标为目标强度ST。

由图1 可以看出，在ka＜ 6时，PMMA 球的目标强度大于钢球，且频率越低，增强效果越明显；随着频率的增加，PMMA 球的目标强度逐渐降低，这是由于PMMA 材料对声波的吸收损耗作用逐渐增强，导致其共振峰幅值被抑制、目标强度减小。

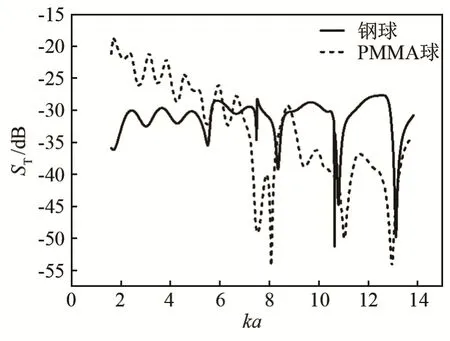
图1 钢球和PMMA 球目标强度随频率变化规律Fig.1 Target strength variation of the steel sphere and the PMMA sphere with frequency

为了研究PMMA 球低频目标强度增大的原因，下面分别计算钢球和PMMA 球的频散曲线。为了计算钢球和PMMA 球的频散曲线，可以应用Watson变换方法求解波数域特征方程Dv( x) = 0的复数根，得到相速度和阻尼因子，但为了避免求复根，本文利用Regge 轨迹跟踪法求解波的相速度[5]。所谓Regge 轨迹是指n 相对于归一化共振频率ka 值的轨迹曲线。对于球来说，达到共振频率时的相速度应满足：

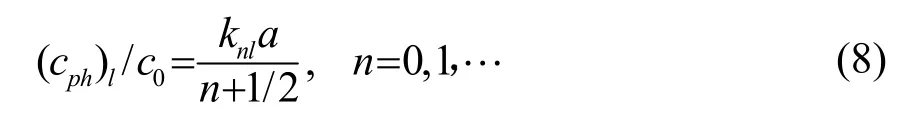
其中：(cph)l为波的相速度；c0为水中声速；knla 为(n , l) 阶归一化共振频率。首先通过分波共振计算出Regge 轨迹图，再根据式(8)计算(cph)l/c0。取l=1 即可得到Rayleigh 波相速度，结果如图2 所示，横坐标为归一化频率ka，纵坐标为cR/c0，cR为Rayleigh波波速。

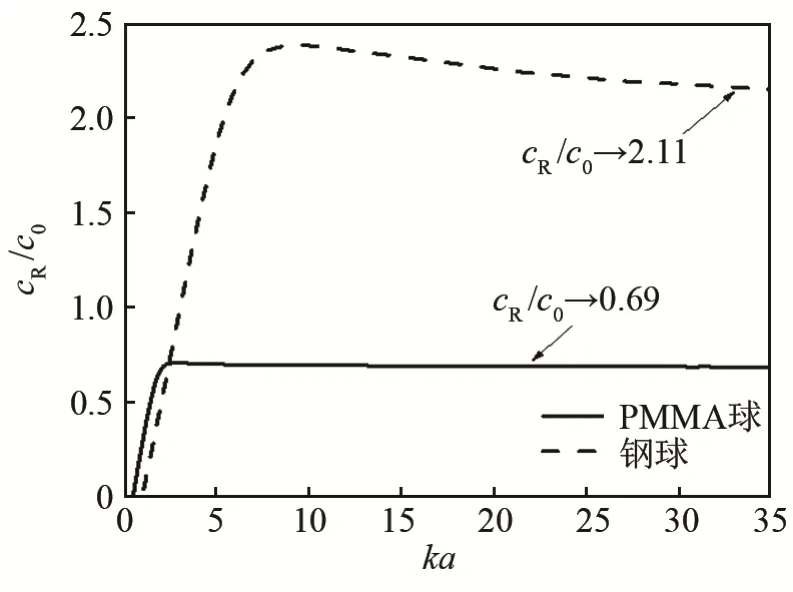
图2 PMMA 球和钢球中的Rayleigh 波相速度频散曲线Fig.2 Dispersion curves of Rayleigh wave phase velocity in PMMA sphere and steel sphere

通过图2 可以看出，在ka 较小时，弹性球Rayleigh 波相速度随ka 的增大快速增大，在ka 较大时，Rayleigh 波相速度趋向无限大介质中Rayleigh波速度，钢球的cR/c0趋近于2.11，而PMMA 球的cR/c0趋近于0.69，即PMMA 球中的Rayleigh 波波速是水中声速的0.69 倍、低于水中声速，是一类亚音速波，而钢球中的Rayleigh 波波速则为水中声速的2.11 倍，高于水中声速，是一类超音速波。

由环绕波理论[5]可以知道，当相速度cR＞ c0时，波以临界角φ= arcsin(c0/ cR)进入和离开弹性体表面，激发生成Rayleigh 表面波，Rayleigh 表面波沿球体表面边传播边辐射，可在流体介质中形成正常传播的波，从而在收发合置处形成反向散射，因此这种Rayleigh 波再辐射一般称为泄漏波。但对于PMMA 材料，其Rayleigh 波速度小于水中声速。一般来说，亚音速波在传播中再辐射进入水中后，会在流体和固体边界形成非均匀衰减波(或称渐消波)。研究表明，在一定条件下，这类波可以通过耦合声学遂道效应通过渐消波场，形成散射场。对于弯曲电介质波导边界的渐消电磁波场，这是常见的特性[8-9]。Marston 在文献[8]中给出了这种耦合声学遂道效应的假设图像解释，如图3 所示。a 和b 分别为弯曲弹性壳体表面的外半径和内半径，cph为壳体内传播表面弹性波的速度，小于流体中声速c0。引入随半径r 变化的局部相速度，则在流固耦合渐消波场区域内波阵面可表示为

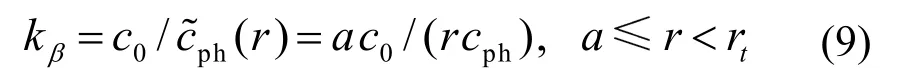
式中，rt=ac0/cph为过渡半径。在a≤ r ＜rt内为渐消波场区域，当r ＞ rt则为非渐消波区域，声线沿rt切线方向正常传播，并向外以表面波辐射阻尼形式再辐射能量。可以认为a≤ r ＜rt的渐消波区域是一种类型的流固耦合声学隧道，这种再辐射是一种声学隧道效应。

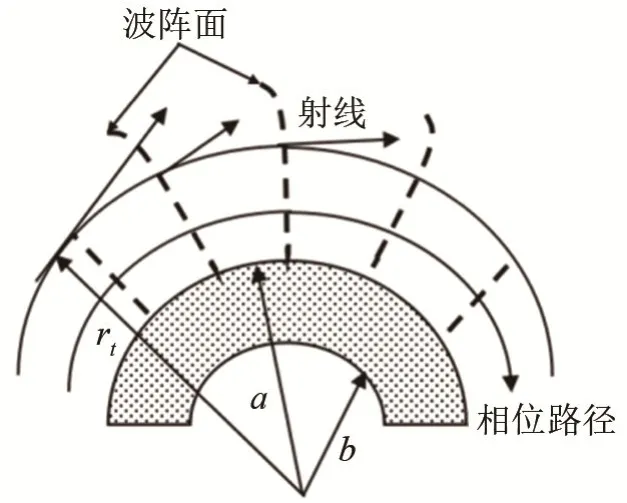
图3 声学隧道效应图像解释Fig.3 Image interpretation of acoustic tunneling effect

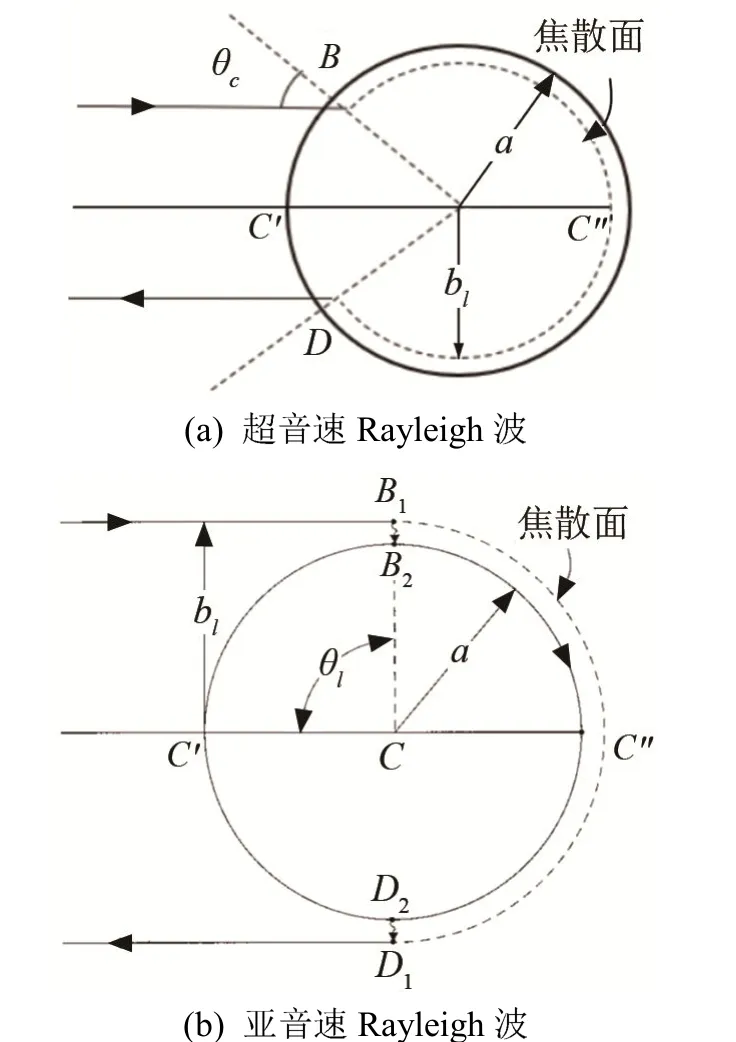
图4 Rayleigh 波传播方式示意图Fig.4 Schematic diagram of the Rayleigh wave propagation

图4 为钢球和PMMA 球的Rayleigh 波耦合传播虚拟路径示意图。半径bl的面为虚拟焦散面，bl=ac0/cR为等效过渡半径。对于钢球，入射平面波在B 点以临界角耦合进入虚拟焦散面，沿BC''D 路径传播，并在D 点处反向散射进入散射声场，此时bl= ac0/cR＜ a 。而对于PMMA 球，入射平面波在B1B2点(弯曲箭头处)耦合进入虚拟焦散面，此时临界角为π /2，bl= ac0/cR＞ a ，在半径a 和半径bl之间为渐消波区域，如同上述的声学隧道，在r ＞ bl区域声线沿半径切线方向正常传播，并向外以表面波辐射阻尼形式再辐射能量，即此时的Rayleigh 波通过耦合遂穿此声学隧道再辐射形成反向散射声场。

与其他弹性材料球类似，当平面声波入射到PMMA 球体时，会产生一系列的环绕波。如图4(b)所示，第一类由环绕波产生的回波是由从B 点进入弹性球表面并以波速cR传播到D 点再出射到水中再返回(或反向传播)的回波。以镜反射回波时间作为时间起点，这个回波的延迟时间包括在水中的传播时间和在球体中传播的时间，可以近似表示为

式中， bl= a×c0/cR。因此，式(10)可化简为

第二个回波是在球体表面又传播一周的回波，因此延迟时间为

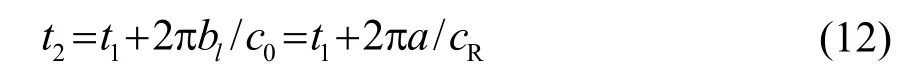
依此类推，第n 个回波的延迟时间是

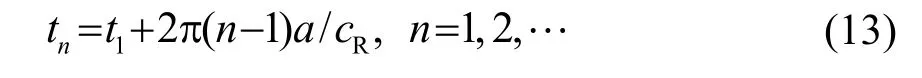
因此，每一个回波的时间间隔为

由环绕波的共振理论可以知道，弹性球表面共振产生的条件是球面周长等于整数个波长加半波长[5]，即：

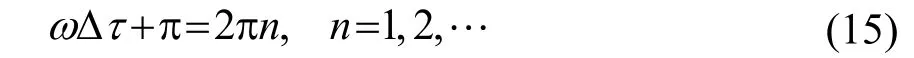
因此，将式(14)代入式(15)可以得到

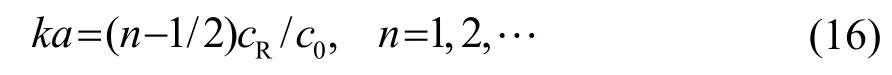
即：

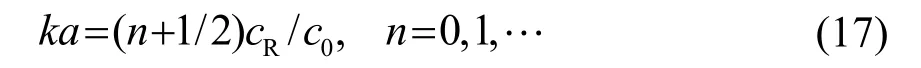
式(17)形式上与式(8)是一致的，根据式(17)即可确定PMMA 球的共振频率ka。

对于金属球等目标，其Rayleigh 波共振频率形式与式(17)是一样的[5]。但是金属目标中Rayleigh波速度cR大于水中声速，PMMA 目标中Rayleigh波速度Rc 小于水中声速，这样导致同样半径尺度的球形目标，PMMA 球的共振频率要低于金属球。如文中金属钢球，其Rayleigh 波共振可能发生在ka＞ 6以上，而PMMA 球则在ka＜ 6时就会发生Rayleigh 波共振。但是由于PMMA 材料对声波的吸收作用随着频率增加而增大，导致其高频目标强度减小。这与图1 中计算得到的PMMA 球的目标强度值的趋势是一致的。

3 实验验证

实验水池大小为5 m×5 m×5 m，实验所用目标分别为半径55 mm 的钢球和PMMA 球，布放图和目标示意图分别如图5 和图6 所示。根据图5，发射换能器距离水听器0.7 m，水听器距离目标1.1 m，三者几何中心位于同一深度，布放于水下2.45 m 处，位于水池中心。实验所采用的发射换能器标定频段为10～20 kHz，水听器型号为BK8103。

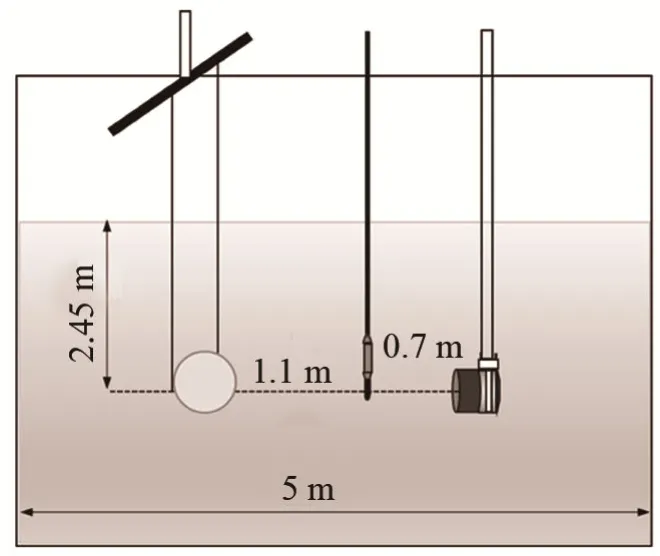
图5 实验布放示意图Fig.5 Schematic diagram of experimental layout

图6 实验所用目标Fig.6 Targets used in the experiment

经过测试，发射换能器在7～15 kHz 频段内的发射响应较好，因此实验测量了目标在7～15 kHz频段内的目标强度。实验采用的发射信号为7～15 kHz 的线型调频(Linear Frequency Modulation,LFM)信号。由于被测目标尺度小，回波信号较弱、信混比低，为了更准确地得到目标的回波信号，首先，利用水听器测量有目标时的回波信号，再移走目标记录无目标时的回波信号，二者相减即可得到目标的回波信号，期间发射信号的形式、幅度等条件保持不变。然后，再将水听器移动至目标球所在位置，记录直达波信号。接着，按照国家标准中的水声目标强度测量方法[10]，对截取的目标回波信号和直达波信号作离散傅里叶变换(Discrete Fourier Transform, DFT)，最后，按照球面波衰减规律计算修正后的目标强度：

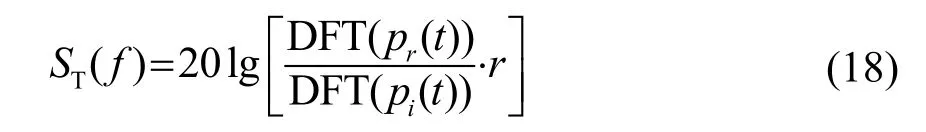
具体过程如图7 所示。

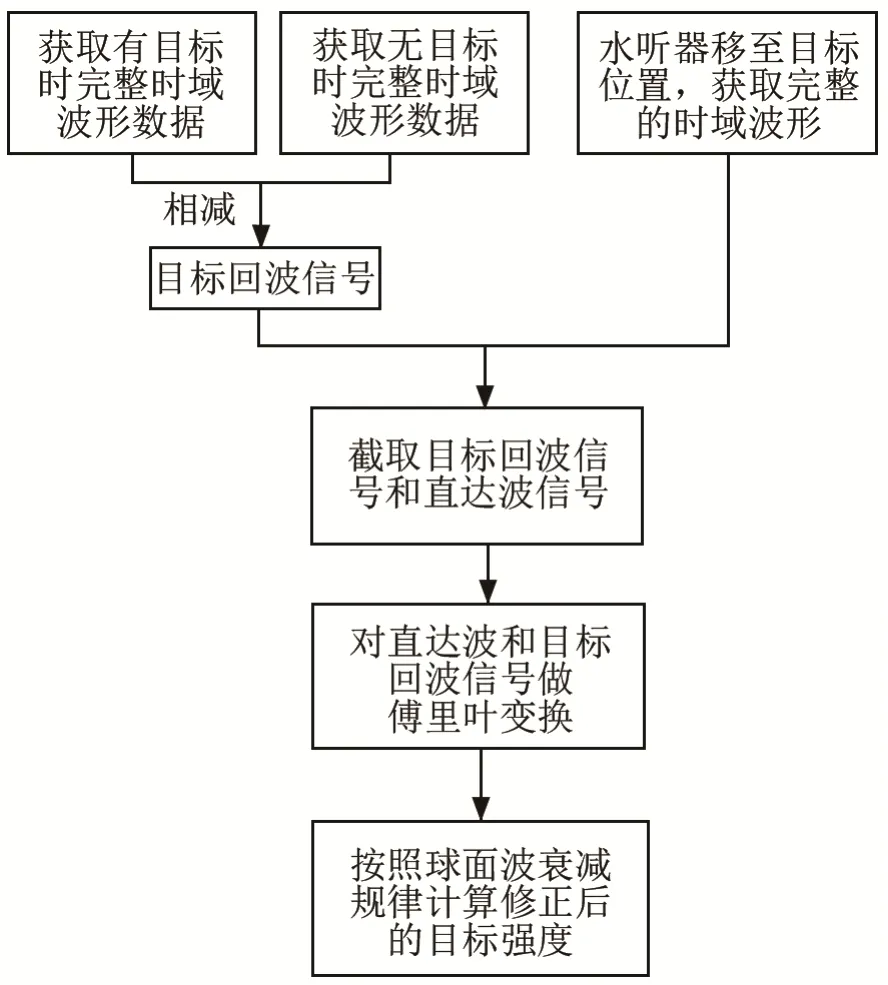
图7 实验数据处理流程Fig.7 Experimental data processing flow

将实验结果与简正级数解(材料参数选取如表1 所示)进行对比，结果如图8 所示。

图8 中的结果表明，实验结果与简正级数解的趋势基本吻合，共振峰位置基本相同，验证了理论计算结果，PMMA 球产生的Rayleigh 波声学隧道效应，其低频目标强度明显大于钢球的低频目标强度。

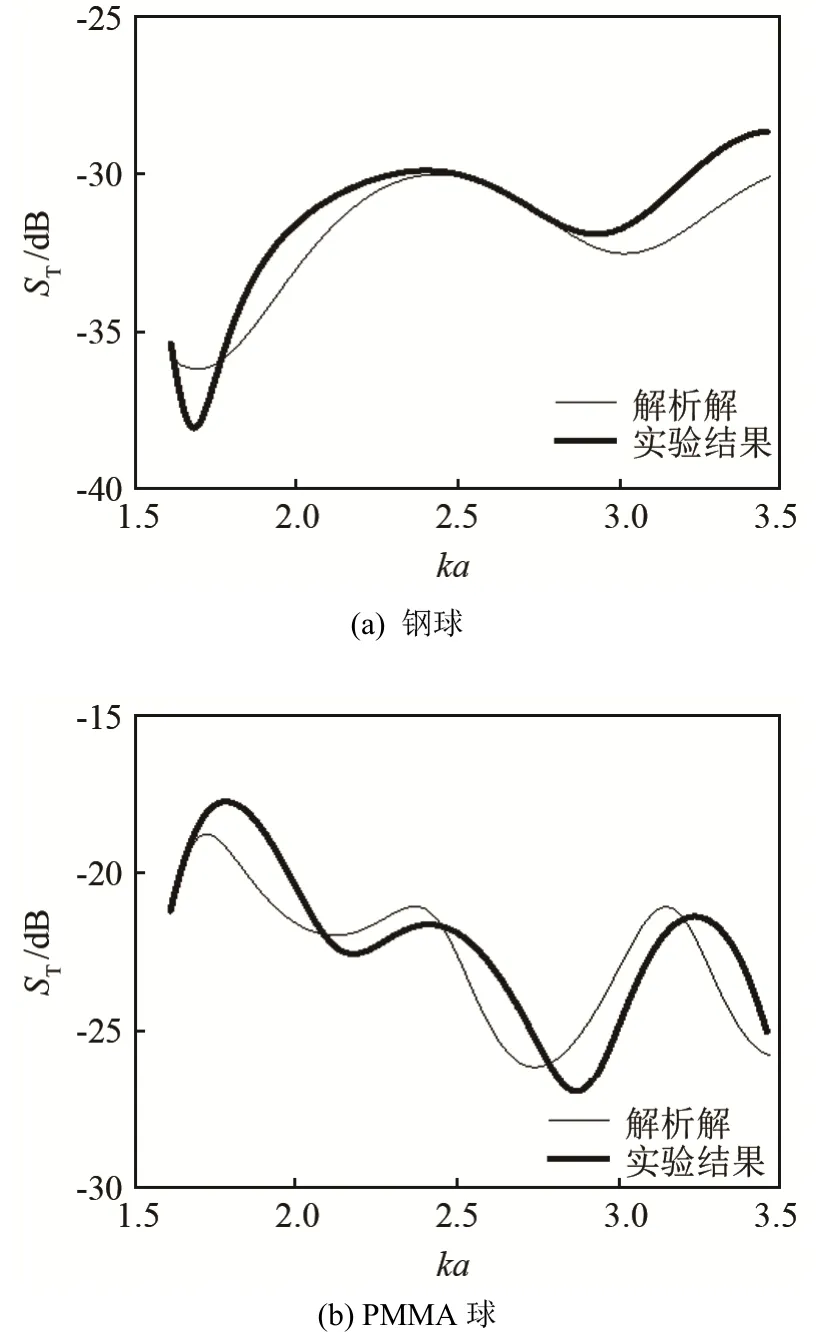
图8 实验测量目标强度与简正级数解对比结果Fig.8 Comparison between the measured target strength and the normal series solution

4 结 论

本文首先利用Rayleigh简正级数解计算了相同尺寸的钢球和PMMA 球的目标强度，发现在低频段(ka＜6)内的PMMA 球目标强度可以比钢球大约6 dB。为了研究低频目标强度增强的原因，分别计算了钢球和PMMA 球的频散曲线，发现PMMA 球中的Rayleigh 波的波速低于水中的声速，在球体表面会产生声学隧道效应，使亚音速的Rayleigh 波能够通过耦合遂穿声学隧道，再辐射形成反向散射声场，从而引起低频目标强度大幅度增强。最后，通过实验对理论计算进行了验证。为实现低频目标强度的增强提供了一种新思路和新方法。

附 录

式(6)中系数矩阵元素dij及、和：