制动夹钳单元输出力传递规律及影响因素分析

曾梁彬, 王贤龙, 陈炳伟

(中车戚墅堰机车车辆工艺研究所有限公司， 江苏常州 213011)

制动系统是轨道交通车辆安全运行的重要保障，基础制动装置作为其中最关键的组成部分之一，是列车其他制动措施发生失效后的最后一道安全保障[1-2]。基础制动装置的传递效率是制动系统设计中的一项重要参数，对精确控制制动距离、提高制动稳定性、优化制动控制策略具有重要意义[3]。

国内许多工程技术人员围绕基础制动装置的传递效率开展了大量研究工作。孙新海[4]研究了货车基础制动装置在空车和重车工况下的静态效率，指出了不同形式闸调器对传动效率损失的影响规律。李伯清[5]结合《列车牵引计算规程》针对货车闸瓦踏面制动的3种传动效率计算方法进行了差异分析，推荐了其中一种相对准确的算法用于评价货车踏面制动装置的实际传动效率。王延哲[6]针对踏面制动装置，利用制动动力试验台，提出了动态传动效率的试验方法，并对比了动、静态传动效率之间的差异与联系。孙家锋[7]从结构原理的角度介绍了几种踏面制动装置的制动倍率计算方法，并对比了不同结构制动装置的制动效率和缓解性能。陈炳伟[8]则针对盘形制动的夹钳单元，通过在不同温度、不同振动工况下的实测制动力与理论制动力的对比，验证了传动效率计算方法的准确性。

基础制动装置实测输出力与理论输出力之间存在差异，一方面是来源于机械传动过程中零部件间的摩擦损失，另一方面则是因理论计算模型自身存在一定误差导致。而理论计算模型误差主要是由于建模过程中对制动装置载荷传递规律的分析存在简化或不完备。以目前动车组平台普遍采用的三点吊挂式制动夹钳单元为对象，从执行机构的工作原理出发，分别研究了制动缸和制动夹钳受到调节轴制动行程、盘片磨耗等外部因素的影响规律，并对传统的输出力计算公式提出了修正。

1 制动缸输出力传递规律

制动缸的功能是将输入气体的压力转化为调节轴的轴向推力。从原理上看，制动缸的输入力Fc_in与气体压力Pc和制动缸活塞有效面积Ap有关，即：

Fc_in=PcAp

(1)

制动缸的阻力一方面来源于传动机构零件之间的摩擦损失，另一方面来源于内部弹簧阻力。一般经验认为，缓解弹簧力是阻力，对制动缸的输出力有直接影响。因此，计算此类制动缸输出力Fc_out的经验公式为：

Fc_out=(PcAp-Fspr)×ηc

(2)

式中Fspr为缓解弹簧工作高度的弹簧力;ηc为考虑制动缸内部零件摩擦阻力后的机械传动效率。

1.1 制动缸输出力模拟

某不带内部放大功能的制动缸的多体动力学分析模型如图1所示。调节轴轴向外侧设置了一个弹性模拟负载，来模拟安装在制动夹钳上实施制动动作时制动缸受到的轴向约束反力。

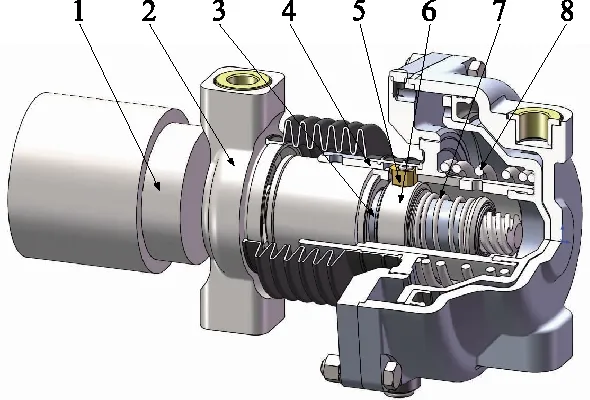
1-模拟负载;2-调节轴;3-调节螺母;4-活塞管导管;5-方键;6-锥齿滑套;7-调节螺母弹簧;8-缓解弹簧。图1 制动缸动力学仿真模型

在制动夹钳单元的实际使用中，夹钳缓解状态的盘片间隙和夹钳杠杆的刚度会影响实施制动动作时制动缸调节轴的实际制动行程(包含空走行程和弹性行程，闸片抱闸前制动缸调节轴的行程为空走行程，闸片抱闸后由于杠杆变形引起的制动缸调节轴行程为弹性行程)盘片间隙越大，或夹钳杠杆刚度越小，调节轴制动行程就相对越大。

针对本节制动缸多体动力学模型，通过调整模拟负载的弹性刚度，可以改变调节轴的制动行程，以此来研究不同制动行程下制动缸输出力的变化规律。

(1)制动行程较小时的输出力

设置制动缸与轴向空走行程5 mm，模拟负载的刚度为K=10 kN/mm，制动缸活塞输入力Fc_in=10 kN，不考虑制动缸的内部摩擦效率损失(假设ηc=100%)。制动缸调节轴的行程和输出力、缓解弹簧力、调节螺母弹簧力的仿真结果如图2所示。

从图2中可以看出，调节轴输出力Fc_out约为8 738 N，制动行程Sc_out约为6.2 mm，工作高度下缓解弹簧力Fspr约为1 263 N，调节螺母弹簧力Fspa约为239 N。在此工况下，输出力Fc_out为输入力Fc_in和缓解弹簧力Fspr二者之差，即满足式(2)关系。

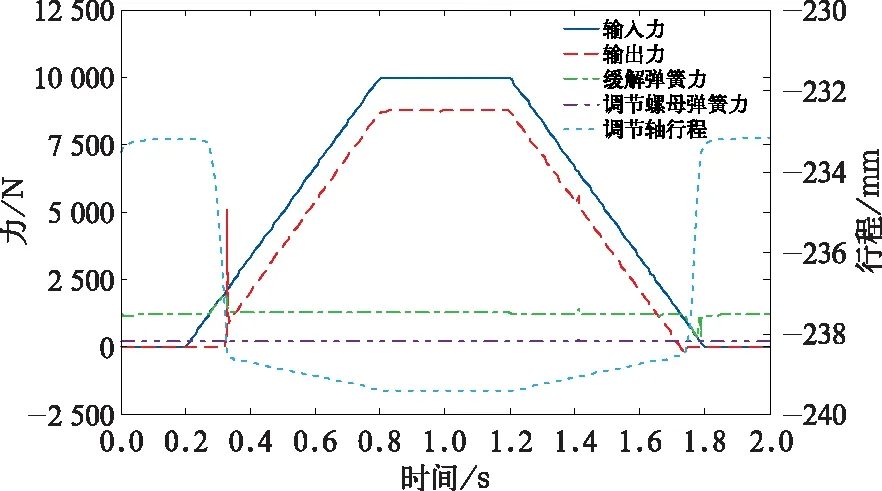
图2 调节轴制动行程较小时的仿真结果

(2)制动行程较大时的输出力

设置制动缸与轴向空走行程5 mm，模拟负载的刚度为K=4 kN/mm，制动缸活塞输入力Fc_in=10 kN，不考虑制动缸的内部摩擦效率损失(假设ηc=100%)。制动缸调节轴的行程和输出力、缓解弹簧力、调节螺母弹簧力的仿真结果如图3所示。

从图3中可以看出，调节轴输出力Fc_out约为8 495 N，制动行程Sc_out约为7.5 mm，工作高度下缓解弹簧力Fspr约为1 270 N，调节螺母弹簧力Fspa约为235 N。在此工况下，各力之间关系并不满足式(2)关系，输出力Fc_out为输入力Fc_in与缓解弹簧力Fspr和调节螺母弹簧力Fspa合力之差。此时制动缸输出力Fc_out的计算公式为：

Fc_out=(PcAp-Fspr-Fspa)×ηc

(3)

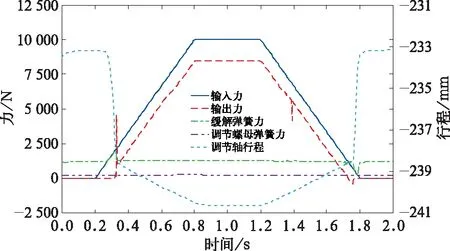
图3 调节轴制动行程较大时的仿真结果

1.2 不同行程下制动缸输出力试验

取两组制动缸样品进行输出力试验，其中一组为正常制动缸，另一组拆除其调节机构，如图4所示。针对两组试验样品，在不发生间隙调整的前提下输入相同气压(375 kPa)，分别测试不同制动行程下的输出力，测试结果见表1和图5。

图4 制动缸输出力测试

从试验结果可以看出，对于不带调节机构的制动缸样品，输出力稳定在10.6 kN附近，基本不随制动行程的变化而改变。

而对于带有调节机构的制动缸样品，随着调节轴制动行程的增大，输出力呈现降低趋势，其中，前两个制动行程下测得的输出力约在10.35 kN附近，后两个制动行程下测得的输出力约在10.59 kN附近，前后相差约0.24 kN，与调节螺母弹簧的理论弹簧力(约0.23 kN)基本一致，说明当制动行程减小后，调节螺母弹簧力转变为制动缸内部阻力，这与上节仿真分析结论相吻合。

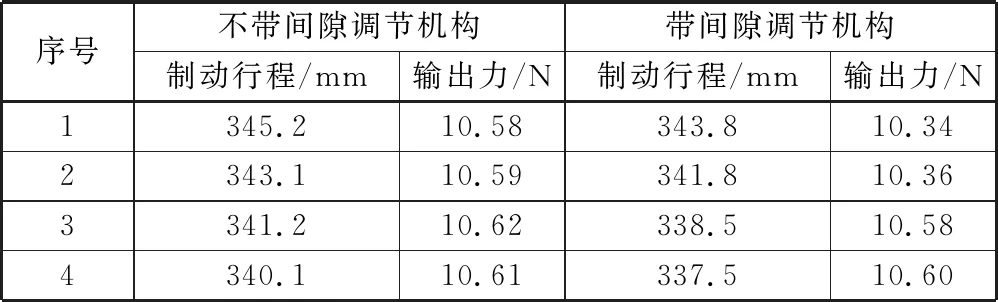
表1 制动缸输出力试验结果

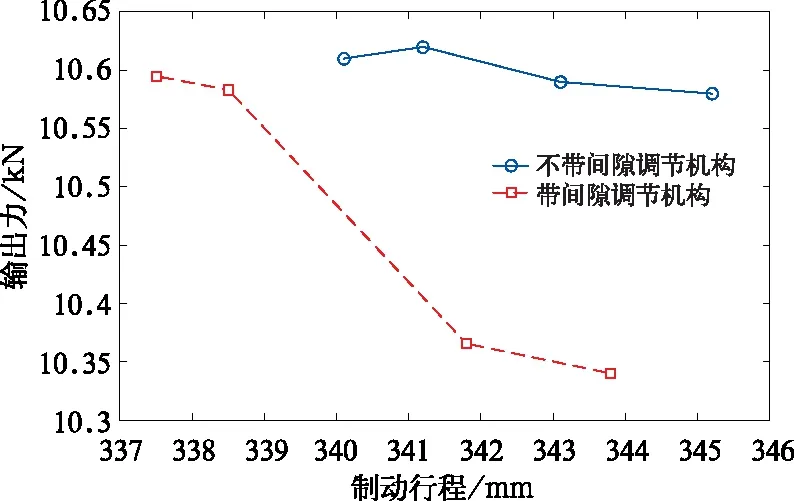
图5 制动缸输出力试验结果对比

1.3 制动缸输出力影响机理分析

图6为两种制动行程下调节机构制动状态的示意。从图6(a)中可以看出，当制动行程较小时，方键未受到活塞管导管上方键槽的轴向限位，调节螺母与锥齿滑套之间的齿面啮合，此时调节螺母弹簧的力为调节机构内力；从图6(b)中可以看出，当制动行程较大时，方键受到活塞管导管上方键槽的轴向限位，调节螺母与锥齿滑套之间的齿面发生分离，此时调节螺母弹簧一端通过锥齿滑套和方键作用在活塞导管上，另一端通过调节螺母作用在调节轴上，故调节螺母弹簧力成为调节轴的阻力。

从上节制动缸输出力试验中也可以发现，当拆除制动缸内部调节机构后，制动缸输出力基本不随制动行程变化而改变，这也进一步验证了上述分析的正确性。

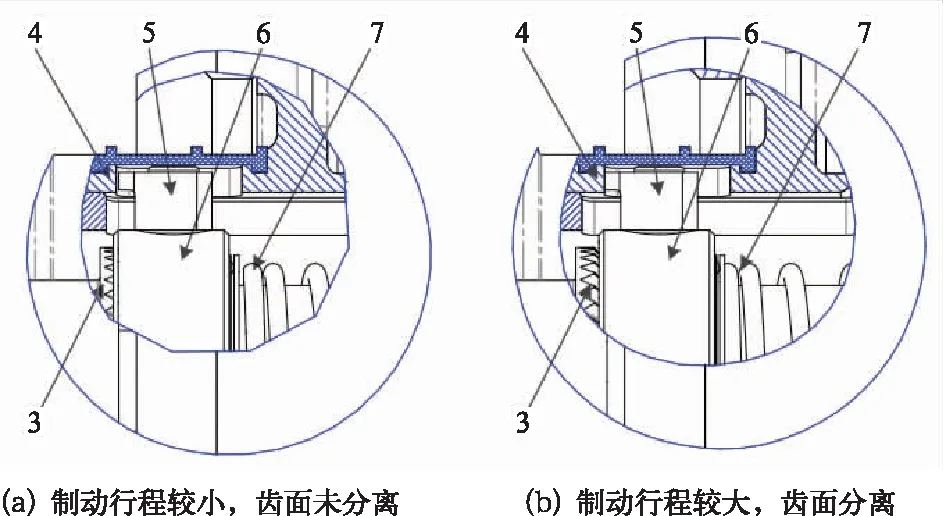
3-调节螺母;4-活塞管导管;5-方键;6-锥齿滑套;7-调节螺母弹簧。图6 不同制动行程下的调节机构状态示意

1.4 制动缸输出力计算公式修正

由上述分析可以发现，制动缸的输出力与制动缸调节轴的制动行程有关，制动行程较小时，制动状态下调节螺母与锥齿滑套的端齿未发生分离，制动缸内部仅缓解弹簧力为阻力；制动行程较大时，制动状态下调节螺母与锥齿滑套的端齿将发生分离，制动缸内部的缓解弹簧力和调节螺母弹簧力均为阻力。由此，式(2)可修正为：

(4)

2 制动夹钳输出力传递规律

制动夹钳是将制动缸提供的轴向推力，以销轴为固定铰接支点，通过杠杆并以一定的放大倍率，转化为双侧闸片的正压力。从原理上看，制动夹钳的动力输入Fl_in来源于制动缸输出的推力，即Fl_in=Fc_out。一般经验认为，制动夹钳的阻力主要来源于传动机构零件之间的摩擦损失，因此，计算制动夹钳的输出力Fl_out的经验公式为：

Fl_out=Fl_in×il×ηl

(5)

式(5)中，il为制动夹钳双侧杠杆比;ηl为考虑制动夹钳零件摩擦阻力后的机械传动效率。

2.1 制动夹钳输出力模拟

某3点吊挂式制动夹钳的多体动力学分析模型如图7所示，该模型的理论双侧杠杆比为3.217。在双侧杠杆末端安装一个模拟制动缸来提供轴向推力，前端双侧闸片之间设置模拟制动盘。

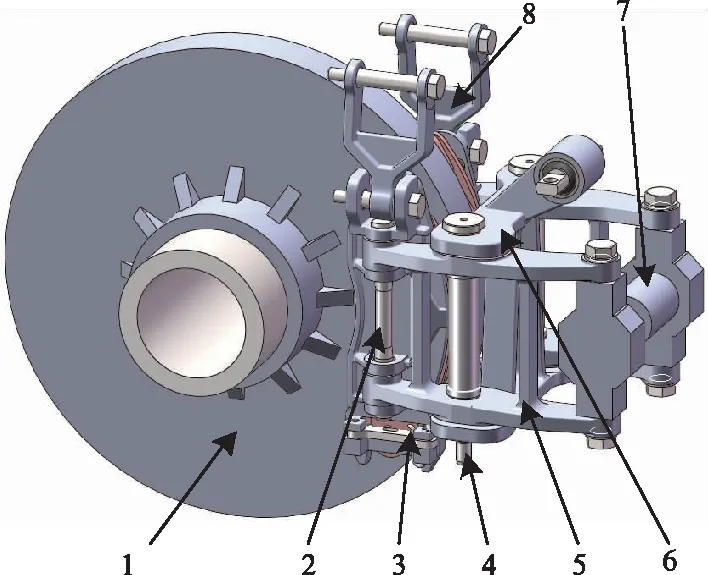
1-模拟制动盘;2-闸片托销轴;3-闸片托;4-销轴;5-杠杆;6-吊架;7-模拟制动缸;8-闸片托吊。图7 制动夹钳动力学仿真模型

在制动夹钳单元的实际使用中，制动盘和闸片的磨耗会改变制动状态下杠杆和闸片托吊的转角姿态。以下针对本节制动夹钳多体动力学模型，通过改变模型中制动盘厚度，来模拟研究不同磨耗状态下制动夹钳输出力的变化情况。

设置模拟制动缸轴向推力Fc_out=Fl_in=10 kN，不考虑制动夹钳的机械传动效率损失(假设ηl=100%)。不同制动盘厚度下制动夹钳的输出力仿真结果如表2所示。

从表2中可以看出，随着制动盘厚度从61 mm变化至66 mm，制动夹钳闸片端双侧夹紧力Fl_out从约32.53 kN 下降至约32.24 kN，发生了较小的变化，制动夹钳的实际放大倍率约在3.224～3.253之间，略高于理论杠杆比3.217。

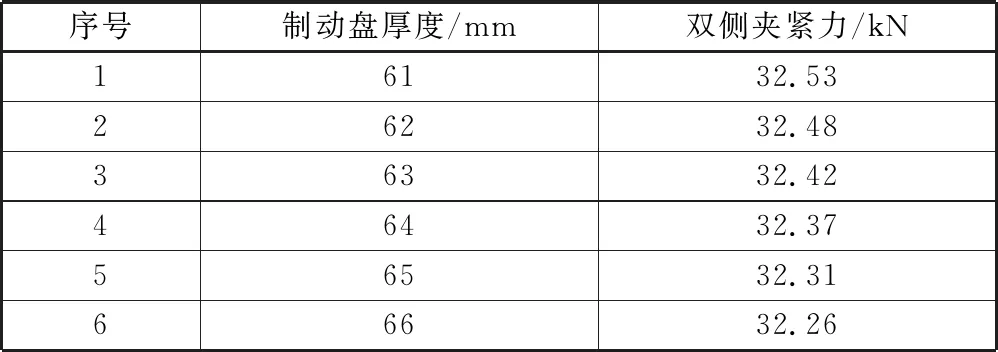
表2 制动夹钳双侧夹紧力仿真结果

2.2 不同制动盘厚度下夹钳输出力试验

为验证上述仿真分析中制动盘不同厚度对制动夹钳输出力的影响，取一组制动夹钳单元样品进行输出力试验，如图8所示。

图8 制动夹钳输出力测试

为消除制动缸自身输出力变化带来的影响，拆除了制动缸内部调节机构，从而可将制动缸的输出力Fc_out视作基本恒定(见上节结论)。调整制动缸输入气压Pc使制动缸输出力Fc_out保持在10 kN附近，通过增加垫片的方式有级调整制动盘厚度，记录不同厚度下制动夹钳闸片端的双侧正压力，结果如表3所示。

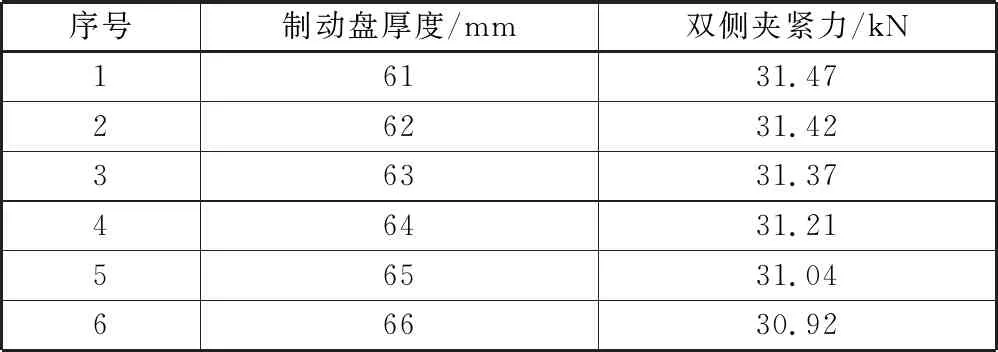
表3 制动夹钳双侧夹紧力实测结果

图9为在对应制动盘厚度下制动夹钳输出力仿真与实测结果对比。从图中可以看出，实测制动夹钳的输出力与仿真结果具有相同的变化趋势，验证了仿真分析结论的合理性。从绝对数值上比较，实测结果整体小于仿真结果，主要是因为仿真分析中未考虑制动夹钳由机械摩擦导致的效率损失。

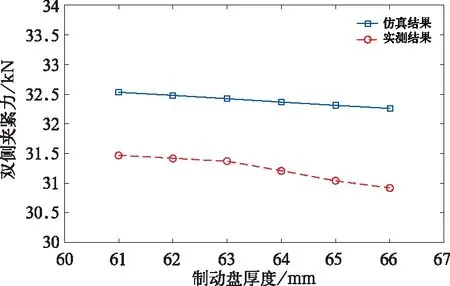
图9 不同制动盘厚度下的制动夹钳输出力对比

2.3 制动夹钳输出力影响机理分析

从原理上看，影响制动夹钳输出力效率变化的因素主要包含以下两方面：闸片托吊的水平约束反力和实际杠杆比的变化。

(1)闸片托吊水平约束反力

图10为制动状态下闸片托的受力状态示意。在制动状态下，闸片托上主要受到来自杠杆的压力Fl、来自制动盘的约束反力Fd，以及闸片托吊的约束反力Fzptd，3个平衡力之间满足以下关系：

(6)

式(6)中α为闸片托吊偏离垂直平面的角度，其值随制动状态下制动盘和闸片的磨耗量有关，Fd水平分量的两倍即为制动夹钳输出的双侧夹紧力Fl_out。

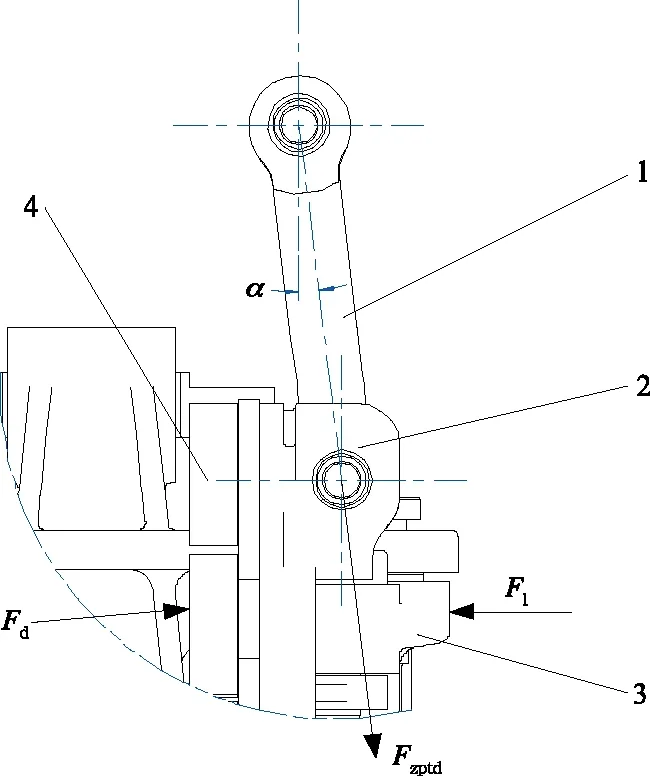
1-闸片托吊;2-闸片托;3-杠杆;4-闸片。图10 闸片托受力状态示意

从图10中不难发现，由于闸片托吊水平约束反力Fzptdsinα的存在，杠杆上的压力在转化为闸片正压力的过程中出现了损失，这部分效率损失的大小与闸片托吊偏离垂直平面的角度α有关，α越大，效率损失越严重。

(2)实际杠杆比变化

制动夹钳杠杆结构如图11所示，A为闸片托销轴孔轴线投影，B为螺纹销孔轴线投影，O为销轴孔轴线投影，其中，O点为转动中心。

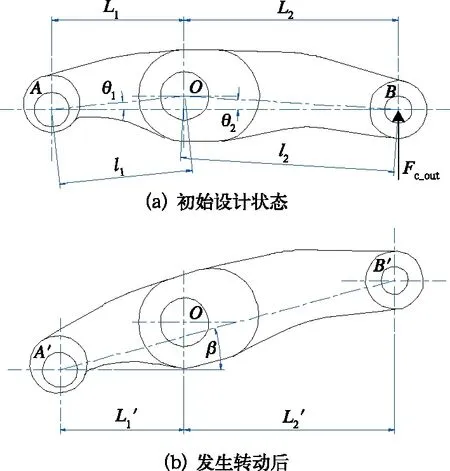
图11 实际杠杆比变化示意

从图中可以看出，A、B、O3点不共线，O点位置相较AB连线存在一定偏移量。在杠杆设计时，通常在制动缸输出力Fc_out方向与AB连线正交状态(初始设计状态)下进行设计，因此设计的理论杠杆比为：

(7)

式中，L1和L2分别为杠杆以销轴为转动支点作用时的前、后段力臂长度，并且有：

(8)

其中，l1和l2分别为销轴孔轴线到闸片托销轴孔轴线和螺纹销孔轴线的距离，θ1和θ2的含义见图11所示。l1、l2、θ1和θ2为杠杆的结构参数，不随杠杆姿态变化而改变。

当制动盘和闸片存在磨耗，制动夹钳杠杆在制动状态下的转角姿态也将发生相应变化。当杠杆在制动状态下的姿态相对于初始设计状态转过一定角度β之后，制动夹钳的实际杠杆比iL′将变为：

(9)

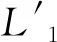
从上式可以看出，当A、B、O3点不共线，即θ1和θ2不为零时，制动状态下杠杆转角姿态的改变将引起实际杠杆比发生变化。其中，销轴孔O位置相较闸片托销轴孔A与螺纹销孔B二者两线的偏移量越大，θ1和θ2也越大，杠杆转角变化引起的实际杠杆比变化也越明显。当A、B、O3点共线时，制动夹钳的杠杆比将保持不变。

由此，式(5)可修正为：

(10)

3 结 论

(1) 制动缸调节轴制动行程的大小会影响制动缸的输出力。制动行程较小时，制动缸内部阻力主要为缓解弹簧力；制动行程较大时，除缓解弹簧力外，调节螺母弹簧力也体现为内部阻力。

(2) 制动夹钳在制动状态下的姿态会影响制动夹钳的输出力，一方面是由于闸片托吊的水平约束反力导致的力传递损失，另一方面是由于制动状态下杠杆姿态角度引起的实际杠杆比变化。

(3) 影响制动缸制动行程的因素主要包括制动夹钳缓解状态下的盘片间隙以及夹钳的结构刚度；影响制动夹钳制动状态下姿态的因素包括制动盘和闸片磨耗，因此，在制动摩擦副材料服役全生命周期过程中输出力会存在一定范围的变化。