混凝土折板式拱网壳动力特性的参数化分析
2020-03-20姜腾钊张华刚王勤征
姜腾钊,张华刚*,魏 威,王勤征,吴 琴
(1.贵州大学 空间结构研究中心,贵州 贵阳 550003;2.贵州省结构工程重点实验室,贵州 贵阳 550025;3.贵州建工监理咨询有限公司,贵州 贵阳 550081)
虽然现代空间结构朝轻质、高强方向发展[1],但混凝土良好的耐久性和防火性是钢材不易替代的,因此混凝土薄壳结构自二十世纪中叶得到大量应用以来[2],至今尚未淡出工程视野,2007年建成的华南理工大学体育馆屋盖为预应力双曲抛物面组合扭壳[3],2011年建成的银川火车站东站房主入口大厅采用了三连跨拱壳结构[4]。
混凝土薄壳施工复杂是不争的事实[5],因此近年来在折板壳及网壳基础上,又发展了若干新型壳体结构,大体有空腹网壳、组合壳或组合网壳、折板式密肋网壳等。马克俭等[6]提出的混凝土空腹网壳,可以理解为是由平面刚架弯曲后交叉组成的双重空间网格结构。滕锦光等[7]提出的钢 混凝土组合壳由钢壳和混凝土壳组成,钢壳既是受力结构又是混凝土浇筑的模板。在带肋壳基础上,将混凝土肋外包U型钢后,常玉珍等[8]提出了组合肋壳结构。将预制带肋板与网壳相连而共同工作,董石麟等[9]提出了组合网壳结构。上述研究工作有效推动了混凝土壳体结构的发展。
混凝土曲面壳施工时,节点坐标控制不准是引起结构几何初始缺陷的重要原因[10],因此张华刚等[11]将曲面壳与密肋平板相结合,提出了混凝土折板式网壳结构。这类结构可通过切割几何体后,再将所切平面网格化而得到,结构坐标主要由脊(谷)线控制,易于施工,工程实践表明,结构具有较好的技术经济指标[12]。
对于混凝土棱柱面网壳,柳勇斌等[13]进行的分析表明,结构具有较强的单向传力性质,因此本文将结构沿纵向多折起拱,提出斜放网格混凝土折板式拱网壳结构,采用有限元方法进行动力特性分析,以期为结构的抗风、抗震计算等奠定基础,并考虑矢跨比、横向脊(谷)线拱、纵向脊线拱、空腹桁架上弦、密肋梁及屋面板刚度等因素对基频的影响,以评估结构刚度,为工程应用提供参考。
1 结构形式及计算模型
1.1 结构形式
结构形式如图1所示,可以理解为双重结构,主结构由横向脊(谷)线拱和纵向脊线拱构成,密肋平板支承在主结构上,纵向脊线拱为多折拱。也可以将其理解成是由网格化的V形折板拱沿纵向排列而成的折面拱结构。纵向框架柱顶需设置空腹桁架等边缘结构封闭拱脚,山墙处可设框架支承屋盖,山墙框架也可与屋盖柔性连接。

1 密肋梁;2 横向脊线拱;3 横向谷线拱;4 纵向脊线拱;5 屋面板;6 边缘桁架上弦;7 边缘桁架腹杆;8 边缘桁架下弦;9 纵向框架柱;10 抗推结构;11 山墙框架柱;12 山墙框架梁;13 天沟。
图1 结构形式
Fig.1 Structure form
1.2 有限元模型
由于本文仅分析屋盖自身的动力特性并评估其结构刚度,因此不计天沟、支座抗推结构及山墙框架的影响,全部算例的基本情况如图2所示,结构跨度为52 m,纵向长度为54 m,支座纵向间距为18 m,每块密肋平板的周边均沿屋盖跨度方向等分为8个网格、纵向等分为5个网格,结构平面布置如图2(a)所示。V形密肋折板拱的拱脚处设置空腹桁架,其顶点高度为结构纵向矢高f2,如图2(b)所示。屋盖剖面如图2(c)所示,结构横向矢高为f1。密肋平板斜放,网格构造如图2(d)所示。
本文以结构自振分析算例为基本算例,在此基础上做影响基频的单参数分析,除需改变截面刚度的构件外,V形拱脚空腹桁架腹杆和下弦杆的截面尺寸均为0.40 m×0.40 m。有限元建模按自然节点划分单元,屋面板为空间板壳单元,其余构件采用了空间梁单元,且板梁的中面重合。支座位置的节点作全部自由度约束,以模拟嵌固支座。计算时除了考虑结构自身质量外,还考虑了外加3.35 kN/m2的荷载转化的质量。混凝土的弹性模量为E=3×104N/mm2,泊松比为ν=0.2。有限元模型如图3所示。

图2 算例基本情况Fig.2 Basic information of examples

图3 有限元模型Fig.3 Finite element model
2 结构自振特性
对于基本算例,取密肋梁的截面尺寸为0.25 m×0.35 m,横向脊(谷)线拱的截面尺寸为0.40 m×0.60 m,纵向脊线拱截面尺寸为0.30 m×0.55 m,空腹桁架上弦截面尺寸为0.40 m×0.50 m,屋面板厚度为100 mm进行结构自由振动分析,前十阶振型如图4所示,对应自振频率如表1所示,前50阶频率分布如图5所示。
结构的前十阶振型主要以竖向振动为主,且关于纵向顶脊线具有对称性,屋盖纵向端部(山墙处)的振型位移均较大,与文献[13]相比,表明屋盖纵向多折起拱后,刚度薄弱位置将移至屋盖的山墙处,而工程应用时,此处至少有山墙框架与屋盖柔性连接,因此屋盖纵向起拱能有效提高结构刚度。
在前十阶振型中,一至七阶振型主要为横向拱的振动,且山墙处的振型位移明显大于其余区域的振型位移;八、九阶振型中,中部区域密肋平板的振型位移较大;十阶振型时,位移较大的区域又出现在山墙处。可见抗震分析时不能只计及低阶振型的影响。
结构前50阶自振频率的分布具有跳跃性,出现相同频率的振型序号较多,这是由于结构具有对称性的缘故。

图4 结构的前十阶振型Fig.4 Top 10 modes of structure
表1 结构前十阶自振频率
Tab.1 Top 10 natural frequencies of structure

振型序号12345678910自振频率/Hz1.9962.4512.5602.8343.5103.7623.8364.0514.4694.685

图5 结构的前50阶频谱Fig.5 Top 50 frequencies spectrum of structure
3 结构基频的参数化分析
3.1 算例情况
在基本算例基础上,除矢跨比外,只调整相应构件的截面高度来考察其刚度对结构基频的影响,算例情况分别为:
(1)仅改变横向矢高f1计算5个算例,f1分别为6.0 m、7.0 m、8.0 m、9.0 m和10.0 m,以考察横向矢跨比对结构刚度的影响。
(2)分别取V形密肋折板拱的矢高f2为1.8 m、2.0 m、2.2 m、2.4 m和2.6 m,以考察纵向矢跨比对基频的影响。
(3)考虑横向脊(谷)线拱的刚度影响时,其截面高度分别为600 mm、700 mm、800 mm、900 mm和1 000 m。
(4)考虑纵向脊线拱的刚度影响时,纵向脊线拱的截面高度分别为400 mm、450 mm、500 mm、550 mm和600 mm。
(5)考虑空腹桁架上弦刚度影响时,取其截面高度分别为500 mm、600 mm、700 mm、800 mm和900 mm。
(6)考虑密肋梁刚度影响时,密肋梁的截面高度分别为350 mm、400 mm、450 mm、500 mm和550 mm。
(7)考虑屋面板的厚度影响时,屋面板厚度分别为60 mm、70 mm、80 mm、90 mm和100 mm。
3.2 横向矢跨比对基频的影响
不同横向矢跨比下的基频计算结果如图6所示。可见基频随结构横向矢跨比的增加而降低,当横向矢高为6 m时,结构矢跨比约为1/8.7,基频为2.16 Hz,而当横向矢高增加到10 m时,矢跨比约为1/5.2,基频为1.94 Hz,降低约10.2%。一般而言,壳体结构的刚度会随矢跨比的增加而提高,但本文的计算结果与此相反,原因在于主拱是屋盖低阶振型的振动节线,屋盖山墙处无支承时,此处是屋盖刚度的薄弱位置,因此工程应用时,此处应予支承,以免低估屋盖刚度。
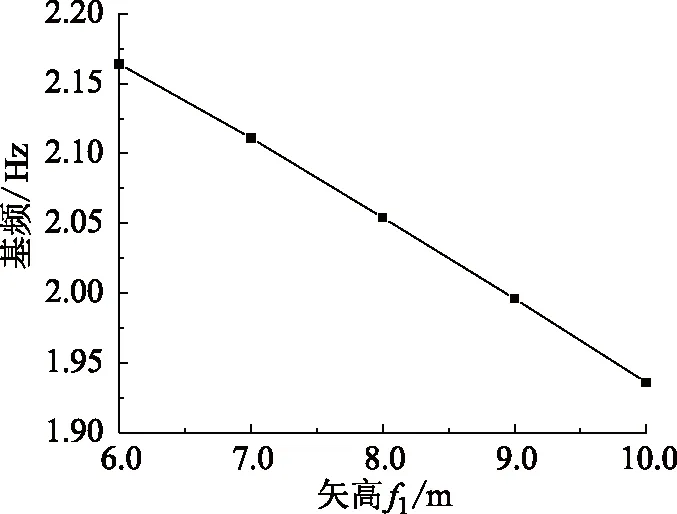
图6 横向矢高对基频的影响Fig.6 Influence of transverse rise for base frequency
3.3 纵向矢跨比对基频的影响
改变V形密肋折板拱的矢高f2后,基频的计算结果如图7所示,表明基频随纵向矢跨比的增加而增加。当f2=1.8 m,约为V形拱自身跨度的1/10时,基频为1.87 Hz;当f2=2.6 m,约为V形拱跨度的1/7时,基频增大为2.25 Hz,增幅约为20.3%,因此提高V形密肋折板拱的矢跨比,有利于增强结构的整体刚度。

图7 纵向矢高对基频的影响Fig.7 Influence of longitudinal rise for base frequency
3.4 横向脊(谷)线拱刚度对基频的影响
改变横向脊(谷)线拱的截面高度后,结构基频的计算结果如图8所示。可见,当横向脊(谷)线拱截面高度由600 mm逐步提高至1 000 mm时,基频近似按线性由1.996 Hz增长到2.371 Hz,增幅约为18.8%,原因在于横向脊(谷)线拱是屋盖的主要传力结构,且是密肋平板的弹性支承,因此增强横向脊(谷)线拱的刚度有利于提高结构的整体刚度。
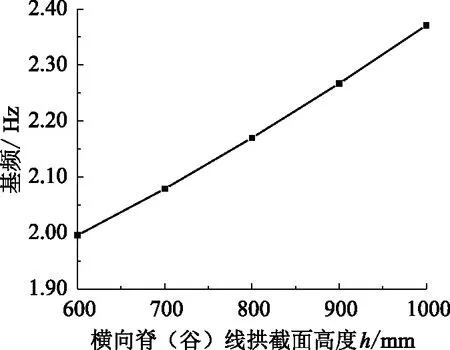
图8 横向脊(谷)线拱刚度对基频的影响Fig.8 Influence of rigidity of transverse ridges(valleys) for base frequency
3.5 纵向脊线刚度对基频的影响
基频随纵向脊线刚度的变化情况如图9所示。纵向脊线截面高度由400 mm渐次增加至600 mm,结构的基频从1.996 Hz变为1.998 Hz,增长幅度几乎可以忽略不计。由于纵向脊线为结构的振动节线,且其靠横向脊(谷)线支承,因此增加纵向脊线的刚度不能提高结构整体刚度。
3.6 空腹桁架上弦刚度对基频的影响
基频随空腹桁架上弦刚度改变的结果如图10所示。上弦截面由0.5m变至0.9m时,基频由1.996 Hz变至2.010 Hz,数值几乎未变,因为V形密肋折板拱是单向传力结构,且主要依靠横向脊(谷)线拱约束其变形,因此提高V形密肋折板拱的拱脚边缘结构刚度,几乎不会影响屋盖的整体刚度。
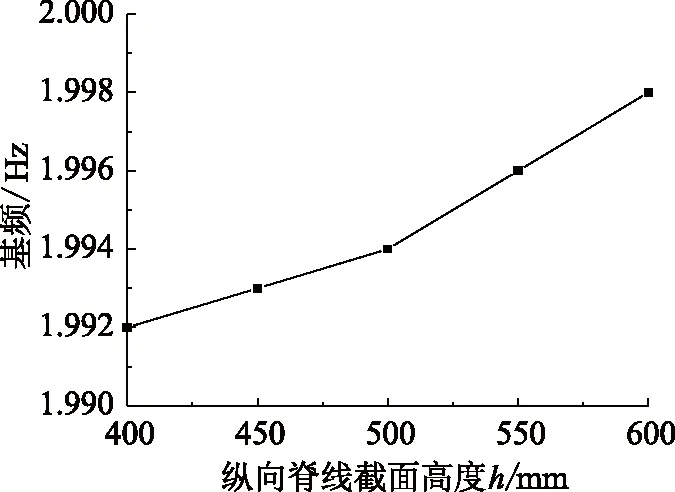
图9 纵向脊线刚度对基频的影响Fig.9 Influence of rigidity of longitudinal ridges for base frequency

图10 空腹桁架上弦刚度对基频的影响Fig.10 Influence of rigidity of vierendeel truss top chord for base frequency
3.7 密肋梁刚度对基频的影响
只改变基本算例的密肋梁刚度,基频计算结果如图11所示。密肋梁截面高度取350 mm时,结构基频为1.996 Hz,当密肋梁截面高度增加至550 mm时,结构的基频为1.966 Hz,几乎没有变化,说明密肋梁质量的增加抵消了其刚度增加对基频的影响。

图11 密肋梁刚度对基频的影响Fig.11 Influence of rigidity of rib for base frequency
3.8 屋面板厚度对基频的影响
结构基频随屋面板厚度的变化情况如图12所示。由于有限元模型的板梁中面重合,因此基频变化幅度不大,屋面板厚度由60mm增加至100mm,基频从1.967 Hz提高到1.996 Hz,仅增长了1.5%。屋面板一般作为这类结构的刚度储备,其厚度可按构造要求确定。

图12 屋面板厚度对基频的影响Fig.12 Influence of thickness of roof for base frequency
4 结论
(1)开敞式折板拱网壳的低阶振型以竖向振动为主,结构的刚度薄弱位置出现在开敞处,因此工程应用时,屋盖纵向两端至少应实现山墙结构与屋盖的柔性连接,以提高结构的整体刚度。
(2)结构横向矢跨比的增加不利于开敞式屋盖的刚度增强,但V形拱自身矢跨比的提高对结构整体刚度的贡献显著。
(3)横向脊(谷)线拱是屋盖的主要传力结构,因此增强横向脊(谷)线拱的刚度可以明显提高结构的整体刚度。
(4)纵向脊线为结构的振动节线,且其靠横向脊(谷)线支承,因此增加纵向脊线刚度对结构整体刚度的影响不大。
(5)空腹桁架上弦作为V形密肋折板拱的拱脚边缘结构,其刚度几乎不影响结构整体刚度。
(6)提高密肋梁的刚度将引起结构的质量增加,因此密肋梁的刚度改变对基频几乎没有影响。
(7)板梁中面重合时,屋面板厚度对结构基频的贡献不大,屋面板可作为结构的刚度储备。
