某新型高速涡旋压缩机转子系统动力特性分析

溥 江，张秀华, *，苏亚锋，姚 宏

(1.贵州民族大学 机械电子工程学院，贵州 贵阳 550025；2.贵州大学 机械工程学院，贵州 贵阳 550025

作为第三代主流压缩机的涡旋压缩机，因其微振低噪、结构紧凑、高效节能、长寿命等优点[1-5]，得到广泛应用。由于其转子为偏心结构，导致系统目前正常工作转速均低于7 000 RPM，极大地限制了系统效率的提高[6-9]。由压缩机制冷量与转速近似线性关系可知，系统工作效率的提升可由工作转速的提高得到。为此，就一最高工作转速为12 000 RPM、制冷量为8 000 W的新型涡旋压缩机转子系统为研究对象，基于转子等效力学模型及动平衡方程，对其临界转速、不同转速下的涡动频率、坎贝尔图及各阶模态振型云图进行分析，为涡旋压缩机转子系统动平衡设计和结构改进提供一定理论参考。

1 涡旋压缩机转子结构

涡旋压缩机是一借助容积变化实现气体压缩的流体机械装置[10]，作为其核心部件的转子结构如图1所示。工作过程为：主轴在电动机驱动下高速旋转，进而带动动涡旋盘绕静涡旋盘旋转，从而形成若干对封闭的月牙形容腔，通过这些容腔的扩大/缩小，完成整机的吸气、压缩及排气过程。

1-动涡旋盘；2-动涡旋盘轴承；3-偏心套；4-主轴承；5-主轴；6-小平衡块；7-电机转子；8-副轴承。图1 涡旋压缩机转子结构Fig.1 Rotor structure of scroll compressor

2 转子系统等效力学模型

对转子系统进行动平衡，是有效降低整机振动、提高系统稳定性、效率、寿命的举措之一[11,12]，该转子系统动平衡等效力学模型如图2所示。

转子受到的力：偏心轴、动涡旋盘及动涡旋盘轴承三者产生的离心惯性力F1，主、副轴承的支反力F2、F4，电机转子两侧小平衡块的离心惯性力F3、F6，偏心套的离心惯性力F5，电机转子的自重G。

图2 转子系统动平衡等效力学模型Fig.2 Dynamic balance equivalent mechanical model of rotor system

由图2得通过主、副轴承形心平面的力矩平衡方程：

A—A面：

F1L1-F5L5-GL2-F3(L2+L3)+F6L6-F4(L2+L3+L4)=0

(1)

B—B面：

F1(L1+L2+L3+L4)+G(L3+L4)+F3L4+F2(L2+L3+L4)-F5(L2+L3+L4+L5)-F6(L2-L6+L3+L4)=0

(2)

式中：F1=ω2r1(m1+m2+m3)

(3)

r1：主轴偏心距；ω：主轴旋转角速度；m1：动涡旋盘质量；m2：动涡旋盘轴承质量；m3：偏心轴质量。

偏心套产生的离心力F5：

F5=m大r2ω2

(4)

式中：m大：偏心套质量；r2：r2偏心套质心至主轴中心线距离。

小平衡块产生的离心力F3：

F3=F6=m小r3ω2

(5)

式中：m小：小平衡快质量；r3：小平衡块质心至主轴中心距离。

电机转子的重力G：

G=m电g

(6)

式中：m电：电机转子质量。

综合以上各式得：

A—A面：

ω2r1(m1+m2+m3)L1-m大r2ω2L5-m电gL2-m小r3ω2(L2+L3)-F4(L2+L3+L4)+m小r3ω2L6=0

(7)

B—B面：

ω2r1(m1+m2+m3)(L1+L2+L3+L4)+m电g(L3+L4)+m小r3ω2L4+F2(L2+L3+L4)-m大r2ω2(L2+L3+L4+L5)-m小r3ω2(L2-L6+L3+L4)=0

(8)

有限元分析得到主、副轴承的支反力，带入相关参数到上述式子可得到两小平衡块及偏心套的质量和位置，这为涡旋压缩机转子系统的动平衡设计提供理论依据。

3 涡旋压缩机转子系统模态分析与临界转速计算

3.1 转子系统有限元分析模型的建立

图1转子系统简化后的模型如图3所示，其部件各物理属性如表1所示。

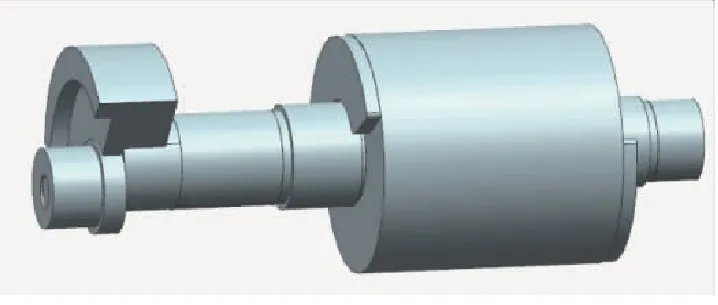
图3 涡旋压缩机转子简化模型Fig.3 Simplified model of scroll compressor rotor

表1 组件物理属性
Tab.1 Physical properties of components

部件材料密度/kg·m-3弹性模量/N·m-2泊松比主轴40Cr78702.11E+110.277偏心套QT60078901.73E+110.3小平衡块铅黄铜85901.05E+110.1电机转子DW310-3577302.18E+110.26

3.2 模态分析求解设置与临界转速计算

(1)网格划分

网格划分如图4所示，节点数45 486，网格单元12 786。

图4 转子系统网格划分Fig.4 Rotor system meshing

(2)边界条件与载荷

电机转子与曲轴为过盈配合，设置电机与曲轴为绑定约束；动涡旋旋盘与动涡旋轴承作为集中质量点添加到动涡旋盘轴承内圈直接接触的表面；添加主、副轴承的约束，并在其内圈接触的内表面分别设置远端位移约束，限制其绕Y轴、Z轴的旋转及沿X轴向移动；添加旋转速度并考虑陀螺效应影响，设置转速0～12 000 rpm,设置后的模型如图5所示。

图5 转子系统边界条件模型Fig.5 Boundary condition model of rotor system

(3)临界转速计算

转子在运转时某一转速的频率与其固有频率相等，会引起剧烈振动[13]。提取该转子前六阶扩展模态，从图6所示的坎贝尔图中可知，转子系统在0 rpm～12 000 rpm转速范围内涡动线与各阶模态频率线没有产生交点，表明转子系统没有产生共振。

由表2所示的转子系统临界转速与不同转速下的涡动频率关系可以看出，各转速下转子涡动特性基本一致，且前6阶涡动方向按前后交替呈现，但前涡动将增加转子刚性，更易激发振动。

图6 转子系统坎贝尔图Fig.6 The campbell diagram of rotor system

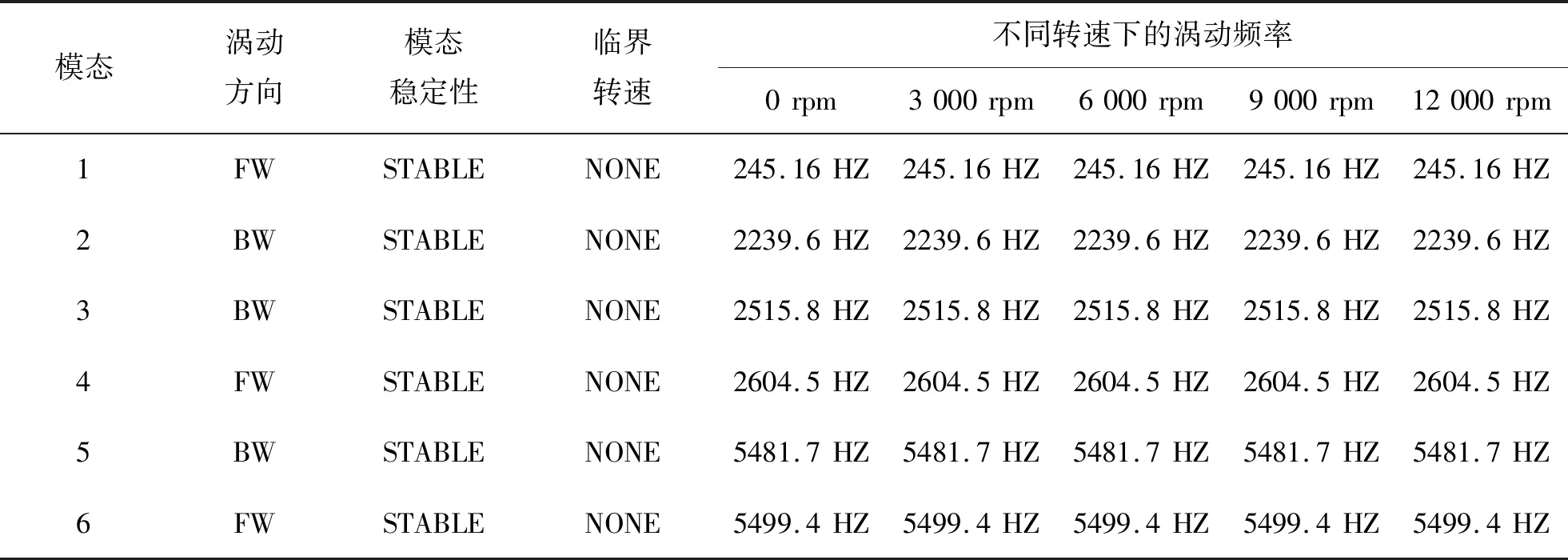
表2 涡旋压缩机转子系统临界转速与不同转速下的涡动频率Tab.2 Critical speed of scroll compressor rotor and its whirling motion characteristics under different rotational speed

图7为该涡旋压缩机转子系统的前六阶振型云图。

结合表2和图7可知，该转子系统第1、4、6阶为正向涡动，2、3、5阶为反向涡动，对于高速转子只考虑正向涡动。且其主要的变形集中在曲轴偏心轴及电机转子处，这与涡旋压缩机转子系统的本身结构有关，符合实际运行情况。

图7 涡旋压缩机转子系统前6阶模态振型Fig.7 The first six order modal characteristics of the scroll compressor rotor system

4 结论

(1)根据涡旋压缩机转子系统结构特点及运行工况，建立其等效力学模型及动平衡方程，为同类型转子系统设计和动平衡分析提供理论依据；

(2)该转子系统模态分析和临界转速计算结果表明：转子经过精确的平衡设计后，在高速工况下，不会产生共振；通过提高曲轴转速来提升涡旋压缩机制冷量的途径是可行的。