窄体通勤车防侧翻主动控制技术研究

冯 磊，何 玲，何康佳，张光星

(贵州大学 现代制造技术教育部重点实验室，贵州 贵阳 550025)

交通拥堵是现代城市面临的主要问题之一，普通四轮车辆的广泛使用加剧了交通拥堵。开发窄小的电动通勤车并将其应用于日常交通中，是解决拥堵问题的有效方法。FURUICHI[1]等人研发了窄体倾斜概念车(NTV)，采用一个前轮两个后轮的车身布局，减小车身宽度。TAN[2]等人在此基础上提出通过被动前轮的方法进行转向。这种窄体通勤车仅需较小的停车位和车道空间。另外，高峰时段道路拥堵情况严重，为保持车辆灵活性，行驶和制动性能十分重要。两前轮一后轮的Tadpole结构[3]布局可以更好适应窄体通勤车面临的拥堵环境。动力学分析表明，在制动过程中，Tadpole结构更稳定，紧急制动时的加速度相比正常驾驶时要高得多[4]。这种结构的车辆，重心位置靠近前轴，在稳态转向的情况下稳定性高。

弯道交通事故频发、危害性大。据2013年中国公安部公开的道路交通事故统计年报看出，全年中，发生在弯道的交通事故高达3.6万起[5]，其中有近九成是因为超速驾驶和操作不当导致[6]。窄体通勤车车身窄，转向时易发生侧翻。为提高侧倾稳定性，TANG[4]等人设计出一种用于窄车身车辆的组合悬架倾斜机构，在进行主动倾斜控制的同时保持车身的紧凑性及轻量性。其严格限制了车辆的倾斜动作方式，使得两个前轮的竖向位移总严格对称，另外该方法没有涉及轮心纵向位移，这一定程度限制了车辆的倾斜动作效率。

上述研究积极推动了窄体通勤车的发展历程，对其转向稳定性的提高提供了可行方案，但并未就车辆位置形态对稳定性的影响进行深入和系统的分析，且未提出具体的倾斜控制动作。这导致以下问题：1)难以确定车辆的倾斜动作对稳定性的影响及其影响程度；2)得不到该模型下的控制策略；3)无法得知该模型下是否存在更加优良的控制策略；4)复杂情况下对现有方案的改进与优化无从下手或需重新着手。

为保证窄体通勤车行驶稳定性，本文在上述车辆模型的基础上，提出一种车轮位置参数可变的车辆模型，类似一种移动服务机器人。该模型基于Tadpole结构，通过改变两前轮的纵向和竖向位置，调整车身位姿，以保证车辆的稳定行驶。提出不同运动状态下，两前轮轮心位置的最优布置方式，使车辆获得良好的行驶姿态和侧倾稳定性。

1 防侧翻主动控制方案

1.1 车辆模型

窄体通勤车模型如图1所示，其关键参数如表1所示。以后轮轮心为原点，纵向为X轴，横向为Y轴，竖向为Z轴(向下为正方向)，建立右手坐标系。行驶过程中，两个前轮相对车身位置可主动变化(dZ1、dX1为内侧轮轮心位移，dZ2、dX2为外侧轮轮心位移)，后轮与车身无相对位移。通过前轮轮心移动调整车身位姿。图2为前轮平衡位置。图3为前轮轮心发生位移时，车辆位姿的变化过程：右轮相对车身抬起，因重力作用落地。左轮相对车身抬起，因重力作用落地。车轮始终与地面接触，浅色线为车轮抬起的假想位置，便于理解与计算。

图2 车辆前轮初始位置Fig.2 Initial position of vehicle front wheel

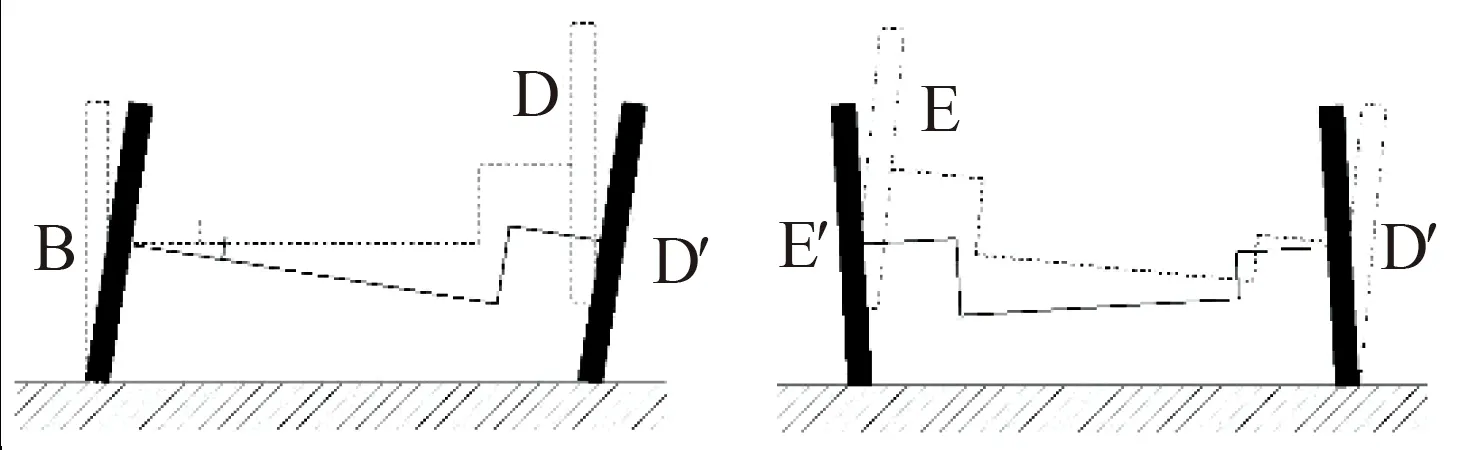
图3 位姿变换示意图Fig.3 Graph ofposture transform

车辆关键参数如表1所示。

表1 车辆关键参数Tab.1 Key vehicle parameters

车辆受力图如图4所示。

图4 车辆受力图Fig.4 Vehicle force diagram

′ 车辆的动力学模型：

Mg=F1+F2+F3

(1)

Mg(YD′-YG″)=F2(YD′-YE′)+F3(YD′-YC)-FR(ZD′-ZG″)

(2)

Mg(XG″-XC)=F1(XD′-XC)+F2(XE′-XC)

(3)

通过式(1)到(3)，可以求得三个车轮在不同位姿下的受力情况。

转向过程中，弯道内侧轮受力最小，是车辆侧翻的判断标准。车辆通过防侧翻控制技术使两前轮轮心发生位移，重力在三个轮子上重新分配，以改善内侧轮受力情况，有效防止车辆侧翻。每个前轮轮心按照什么轨迹发生位移，可使车身快速地完成倾斜，是值得探究的问题，其结果为两前轮轮心运动轨迹。另外，在不同的行驶速度和转弯半径的影响下，车辆倾斜的理想动作会发生改变，两轮心位移至什么位置最有利于车辆稳定安全地通过弯道，同样值得深入研究，其结果为两前轮协调运动方案。两前轮的轮心运动轨迹和协调运动方案组成了窄体通勤车的防侧翻主动控制方案。

1.2 两前轮的轮心运动轨迹

两前轮轮心位移对三个轮子所受地面支持力存在影响，如图5所示。图5(a)为外侧轮不发生运动时，内侧轮所受支持力关于其轮心运动的等高线图。图5(b)为内侧轮不发生运动时，内侧轮所受支持力关于外侧轮轮心位移的等高线图。

先前工作已知，两前轮同时发生位移相比于单独发生位移，内侧轮所受支持力随两前轮轮心位移的变化趋势和取得最大最小值的位置几乎不发生改变。例如当外侧轮发生位移时，内侧轮支持力仍类似图5(a)，其趋势和最值位置不变，只是数值发生了改变。可以认为，每个前轮轮心都存在一条最优运动轨迹，轮心在这条轨迹上运动可使支持力对轮心运动的灵敏度最高。考虑到不同方向的弯道，内外侧轮不固定，可相互转换，所以两前轮采用同一条轨迹，该轨迹需同时包含内外侧轮位移信息。车辆经过连续弯道时，需将车身回正后再进行下一次转弯，故两个前轮的最优运动轨迹应存在公共点，且公共点在平衡位置(原点位置)。为使支持力对轮心位移灵敏，在最优运动轨迹上，轮心走过的距离应为最短。因此，以轮心纵向位移为横坐标，竖向位移为纵坐标，每个前轮的最优运动轨迹即为支持力最大值点与平衡位置的连线，如图6所示，公式(4)和(5)描述了两前轮纵向位移和横向位移的关系。

dX1=dZ1

(4)

dX2=-dZ2

(5)

为增大内侧轮所受支持力，内侧轮总向上(Z轴负方向)移动，外侧轮总向下移动。轨迹表述轮心纵向和竖向位移间的关系。若车辆向右转弯，右前轮为内侧轮，左前轮为外侧轮，此时，右前轮按照图6中实线轨迹向上抬起，左前轮按照图6中虚线轨迹向下放置，直到通过弯道，两前轮按照原轨迹返回平衡位置；若向左转弯，左前轮按照实线轨迹

图5 两前轮位移对内侧轮支持力影响Fig.5 Influence of two front wheels' displacement on inner wheel’s support force

图6 轮心最优运动轨迹Fig.6 Optimal trajectory of wheel center

向上抬起，右前轮按照虚线轨迹向下放置，直到通过弯道，两前轮按照原轨迹返回平衡位置。

1.3 两前轮协调运动方案

两轮同时运动与单独运动达到的效果相同，但前者所用时间明显缩短，响应速度明显增加，车辆转向和变道的稳定性明显增强，相比于后者更优。车辆在不同行驶速度和转弯半径下，两前轮轮心的最优位置不同。因车辆倾斜的动作主要由两前轮的竖向坐标控制，现以行驶速度为横坐标，转向半径为纵坐标，两前轮轮心的竖向位移为竖坐标，得到三维曲面图，定义为最优协调曲面。最优协调曲面表述了两前轮同时位移的最佳配合方案。在确定最优协调曲面的过程中，需要考虑多个衡量目标，以得到综合性能最为出众的曲面。这是一个多目标优化问题。

汽车的横向载荷偏移率(RI)被广泛应用以描述车辆的侧翻危险程度，实用性强[7]，相关研究也进一步表明,以RI值作为车辆侧翻指标具有较高的可信度[8,9]。

(6)

式(6)中，F1和F2分别为内侧轮支持力和外侧轮支持力。RI∈[0,1]，其值越小，对侧翻的抵抗能力越强。故采用RI为一个寻优目标。

车身倾斜是主动倾斜技术避免不了的情形，但其不仅会增加车辆的横向空间占用情况，使驾驶员产生错误的预判，同时也会对驾驶员产生一定的负面影响，使得发生事故的可能性增加，也影响驾驶员的体验。因此，在车辆侧倾稳定性足够的情况下，获得更小的车身倾斜角不仅是一个技术问题，更是一个安全问题，同时也牵扯到乘坐舒适性问题[10]。舒适性良好的车辆，驾驶员不会很容易感觉到疲劳，在一定程度上保障了车辆的安全行驶[11]。将车身倾斜角α作为一个寻优目标，汽车转弯过程中，α越小，驾驶体验越好，危险越小，越符合设计初衷。

协调曲面的寻优问题简单来说是一个多目标的寻优问题，目标函数为RI和α。两者均以小为优。但α越小，转弯时的车辆稳定性越不容易得到改善，RI会越大。两个目标相互既关联又矛盾。

2 协调运动方案寻优

2.1 改进多目标粒子群算法

粒子群算法由EBERHART博士和KENNEDY博士提出，是一种基于群体觅食的单目标智能优化算法[12]。粒子群算法经典、高效，具有收敛速度快、参数设置简单、易于编程实现的特点[13]，因此被广泛应用于各个领域。它从随机解出发，利用群体中的个体对信息的共享，追随当前搜索到的最优解来寻找全局最优，并通过适应度来评价解的品质[14]。

多目标优化是一种考虑多指标的寻优策略，更符合于实际问题的多种决策需求[15]。本文改进的多目标粒子群算法(Improving Multi objective Particle Swarm Optimization)整体流程和标准粒子群算法大致相同，但在粒子维度以及最优解选取处进行了较大改动。

两前轮轮心位置的最优协调曲面的每一个点都确定且唯一，故Pareto最优解集并不能满足要求，需加以处理。本文在“α—RI图”中定义了一条过原点的基准直线，α=K×RI(K>0)。定义Pareto解集的各个点中距离此条直线最近的点为最优解。当K的取值较小时，直线的倾角较小，靠近RI轴，远离α轴，更侧重于对α的优化；反之，更侧重于对RI的优化。窄体通勤车服务于城市，需根据不同的道路环境进行针对性设计，以增大适应性和减小资源浪费。不同的道路环境，K的取值有所不同。车辆主要面向城市道路，时常拥堵，车与车的横向间距需严格把控，故对车辆倾斜角度要求较严格，取K=3.732，即直线的倾角为60°。

2.2 两前轮位移协调控制曲面

以行驶速度为横坐标，转弯半径为纵坐标，竖向位移为竖坐标，将寻优结果绘制成三维曲面图，称为两前轮位移协调控制曲面，如图7所示，其中颜色映射竖向位移。

图7 协调控制曲面Fig.7 Coordinate control surface

协调控制曲面反映了窄体通勤车在不同行驶速度和转弯半径的条件下，两前轮轮心的最优竖向位移。因该图采用离散点插值得到，且内侧轮受力情况与两前轮的位移情况存在非线性关系，故部分曲面不平整，但图中不平整的部分均为外凸，符合实际情况。

图7中两区域均为车辆倾斜区域，边界是其界限。两个区域的曲面部分是轮心位移可调节情况下的最优竖向位移，其中外侧轮为正，内侧轮为负；平面部分表示轮心达到极限位置但车辆不发生侧翻情况下的最优竖向位移，其边缘为一定半径下车辆可承受的最大行驶速度和不同行驶速度下的最小转弯半径。从图中可以看出，随着转弯半径的增大，车辆的最大行驶速度有显著增加；随着行驶速度增大，车辆的最小转弯半径有显著增大。另外，可以观察到两前轮轮心变化近似对称，车辆倾斜的轴线近似在车辆横向的中心位置，此时轮心位置的变化仅引起车辆倾斜，不会或轻微引起车辆俯仰，有利于车辆稳定。

图7中取转弯半径为10 m的截面，得到图8。

图8 轮心竖向位移-速度曲线(R=10 m)Fig.8 Vertical displacement Speed (R=10 m)

图8展示了半径为10 m的弯道处，两前轮轮心竖向位移与行驶速度的关系。从图上可以看出，车辆最大行驶速度为34 km/h。随着车速的增加，内侧轮首先达到极限位置，外侧轮紧随其后，两者近似同步对称变化。如转弯半径为10 m，行驶速度为10 km/h时，内侧轮抬起4.34 cm，向后放置4.34 cm，外侧轮落下4.70 cm，向后放置4.70 cm。

3 仿真试验

3.1 评价指标

窄体通勤车是新型车辆，评价体系尚未有标准，本文立足于车辆的可实行性，以内侧轮支持力为核心约束，经过分析给出以下指标对窄体车辆的转向性能进行评价，以期得到适用于窄体通勤车的评价模型。

1)最大行驶速度和最小转弯半径

一般认为车辆的最大行驶速度Vmax为内侧轮处支持力为零时的速度，最小转弯半径Rmin为内侧轮处支持力为零时的转弯半径。车辆转弯时速度不能过大，转弯半径不能过小，否则会产生较大的离心力，即使车辆应用防侧翻控制技术，但当离心力过大，车辆仍不可避免地会发生侧翻，因此车辆转弯的最大行驶速度和最小转弯半径可以衡量一辆车的侧倾稳定性。一般认为Vmax越大、Rmin越小，车辆的侧倾稳定性越高。另外，越高的最大行驶速度和越小的转弯半径可以给予车辆更高的行驶效率和更灵活的操作体验，也是车辆需要的性能指标。

2)支持力均衡系数Ba

三个轮子所受地面支持力的合力等于车身所受重力4900 N。若某个车轮所受支持力远大于或远小于另外两者，则必定存在至少一个车轮所受支持力接近于零，此时车身极易发生侧翻。换而言之，三个轮子的地面支持力相差越小，车身越不容易发生侧翻。现定义支持力均衡系数Ba(Balance)，计算公式如下：

(7)

其中F1、F2、F3分别为内侧轮、外侧轮和后轮所受地面支持力，均为正。

Ba的变化如图9所示。其范围为[0,1]。Ba=0时，支持力集中于一个轮子，分布极不均衡；Ba=1时，三个轮子所受支持力相等，分布最均衡。在(0,1)上，Ba越大支持力分布越均衡。

图9 不同支持力分布情况下的BaFig.9 Ba under different support force distribution

3.2 仿真实验

实验一：采用Matlab，根据公式(1)到(3)，分别计算车辆施行防侧翻控制前后，不同转弯半径下车辆的最大行驶速度，结果如图10所示。

图10 最大行驶速度曲线Fig.10 Curve of maximum driving speed

相比未带有主动倾斜技术的窄体通勤车，带有该技术的车辆在相同转弯半径下可以承受更大的行驶速度，且半径越大增加幅度越大。如图10所示，以转弯半径为20 m为例，未配备主动倾斜技术的车辆最快只能达到17 km/h，在急转弯时几乎必然发生侧翻，而配备主动倾斜技术的车辆，其最大行驶速度达到了47.5 km/h，相比之下，提升了近179%。即使在急转弯时，允许的最大行驶速度也近10 km/h，极大地增加了车辆的安全行驶范围。窄体通勤车安全性有了极大提升。

实验二：采用Matlab，根据公式(1)到(3)，分别计算车辆施行防侧翻控制前后，不同行驶速度下车辆的最小转弯半径，结果如图11所示。

图11 最小转弯半径曲线Fig.11 Curve of minimum turning radius

如图11所示，在相同行驶速度下可以承受更小的转弯半径，且速度越大减小幅度越大。以20 km/h为例，未配备主动倾斜技术的车辆最小转弯半径为8 m，配备主动倾斜技术的车辆最小转弯半径为3 m，相比减小了62.5%。窄体通勤车的灵活性有了极大提升。

实验三：取转弯半径范围R∈[1 m,20 m]，采用两辆窄体通勤车，一辆采用防侧翻控制技术，一辆未采用，于不同转弯半径和不同行驶速度下，探究车辆支持力均衡系数的变化情况，结果如图12和13所示。曲面边缘为车辆的最小转弯半径和最大行驶速度。

同样的行驶速度下，最小转弯半径大幅度减小图12 无防侧翻控制技术Ba变化Fig.12 Ba without anti roll over control technology

从图12可以看出，未带有防侧翻控制的车辆三个轮子的支持力分布不均匀。在行驶速度较小且转弯半径较大时，Ba近似为1；行驶速度和转弯半径越向边缘靠近，支持力均衡系数越小，且减小速度越快；在曲面边缘时Ba为0，车辆极容易发生侧翻。

图13 带有主动倾斜技术Ba变化Fig.13 Ba with anti roll over control technology

从图13中可以看出，带有防侧翻控制的车辆三个轮子的支持力分布十分均匀。轮心位置可调节时，支持力均衡系数Ba的值近似恒为1，三个轮子的支持力分布近似达到了最均匀的情况，此时车辆稳定性最高；当轮心达到最大位移时，随着行驶速度的增加和转弯半径的减小，Ba值也逐渐减小，但仍大部分集中在0.6左右，只有在可行域的边缘才逐渐变化为0，这说明带有防侧翻控制的车辆可以最大程度地保证三个轮子的支持力分布均匀，相比未配备防侧翻控制的车辆，支持力分配更为合理，稳定性更高。

4 结论

本文提出了一种轮心位置可变的窄体通勤车，并通过受力分析与数值计算确定了窄体通勤车的两前轮轮心的运动轨迹，即内侧轮纵向位移与横向位移成正比关系，外侧轮成反比关系。通过改进多目标粒子群算法对两前轮的运动加以协调，获得了窄体通勤车的防侧翻控制方案。应用此方案，在遇到弯道时，给定不同行驶速度和转弯半径，可以得到两个前轮纵向和竖向的位移量，使得车辆更加稳定地通过弯道。

通过实验对比发现，施行该方案的窄体通勤车相比未施行的车辆，同样转弯半径下，最大行驶速度提高了至少一倍。同样的行驶速度下，最小转弯半径大幅度减小。另外，施行该方案的车辆三个轮子所受地面支持力近似恒为常数，车辆的安全性和稳定性有了极大的提高。