基于反向学习策略的深度搜索布谷鸟算法

何 庆，黄闽茗，周晓南

(1.贵州大学 大数据与信息工程学院，贵州 贵阳 550025;2.贵州大学 学报编辑部，贵州 贵阳 550025)

布谷鸟搜索(Cuckoo Search，CS)算法是在2009年开发的自然启发式算法。该算法基于布谷鸟育雏行为的寄生性，并包含鸟类和果蝇的levy飞行行为[1]为雏形设计算法原理。由于其简单性和有效性，从诞生之日起，吸引了很多学者的关注，并成功应用于工程优化和函数优化问题[2-3]以及机器学习[4]等方面。但是，对于一些复杂的问题，CS算法也存在着局部搜索能力较差、后期收敛速度慢[5]等缺点，暂时无法满足最优解的精度要求，因此其性能需要进一步改进。

王凡等[6]通过分析CS算法的Markov链模型，证明了CS算法的收敛性。张燕[7]提出了一种基于Cubic混沌模型的自适应布谷鸟优化算法，自适应的调整levy flights的随机搜索补偿因子，并Cubic混沌映射嵌入算法，通过实验证明了有效性；汪峰坤等[8]提出的一种改进的布谷鸟算法，通过交叉操作和变异操作，增强了布谷鸟算法的种群多样性和搜索性能。

基于以上算法的启发，本文设计了一种改进的深度搜索布谷鸟(Deep Search Cuckoo Search，DSCS)算法。改进算法引入反向学习策略和逐维深度搜索策略来改进基本的CS。首先，对Levy飞行后的解进行反向学习，提升最优解的搜索效率；然后，对迭代结束后的全局最优解进行逐维深度搜索，捕捉潜在的最优解，弥补搜索步骤可能出现的问题，提高了算法的全局搜索能力。通过5个测试函数的实验结果证明，本改进的DSCS算法具有更好的全局搜索能力，搜索精度和收敛速度。

1 相关工作

1.1 布谷鸟算法

CS算法通过模拟布谷鸟的寄生繁衍策略来寻找最优解。寻找最适合产蛋的鸟巢是一种随机的或类似随机的方式。其基本原理就是把布谷鸟所寄生的鸟巢位置映射为算法种群空间中的解，以寄生巢位置的优劣作为算法的适应度值，为了模拟布谷鸟的繁衍机制，CS算法设定了三个理想规则[1]：

规则1每只布谷鸟只产一个蛋，并随机放入所选择的寄主鸟类的巢穴中。

规则2每次进化都保留最优蛋的巢穴到下一代。

规则3可用的寄主巢穴数量固定，且寄主鸟类以概率R∈(0,1)发现布谷鸟放的蛋。寄主发现布谷鸟的蛋，可以消灭该蛋或放弃旧巢另建新巢。

根据这三条规则，CS包括四个步骤，初始化，搜索，选择和判断。该步骤如下：

(1)初始化

定义目标函数F(x)，并随机生成N个鸟窝的初始位置Xi=(1,2,…,N)，设置问题维数、发现概率Pa和最大迭代次数等参数。

(2)搜索

选择目标函数并计算每个鸟窝位置的目标函数值，得到当前的最优函数值，根据levy飞行生成新的鸟巢位置，计算每个蛋的适应度函数Ft，比较存优。levy飞行的随机步长公式为[1]

xt+1,i=xt,i+α0⊗Levy(β)。

(1)

式中：xt+1,i为巢穴位置更新后的位置；xt,i为当前巢穴位置；α0为步长缩放因子，通常为0.01[2]。

莱维飞行随机搜索路径公式为

(2)

式中：u和v为标准正态随机变量，β为莱维飞行的控制因子，通常为1.5[1]。Φ的计算公式为

(3)

(3)选择

依据布谷鸟的蛋发现概率Pa丢弃不好的巢穴位置，用式(3)更新巢穴中蛋的位置，并计算目标函数Ft，选择存优。位置更新式(3)为

xt+1,i=xt,i+r(xt,j-xt,k)。

(4)

式中：r为比例因子，是(0,1)区间的均匀分布随机数；xt,j和xt,k为t代中的两个随机解。

(4)结束判决

若满足预设的求解精度或最大迭代次数，则结束，否则返回步骤(2)。算法的实现过程如图1描述。

1.2 反向学习

反向学习(Opposition based Learning，OBL)被TIZHOOSH[9]2005年提出，是智能计算领域中的一种新技术。直到2008年，它才被RAHNAMAYAN等[10]用于差分进化算法。OBL是计算可行解决方案的基于反向的解决方案，同时评估原始解决方案和基于反向的解决方案，并选择更好的解决方案[11]。

定义1若x∈[a,b]之间的任意实数，则x的基于反向学习的数如下所示：

x′=a+b-x。

(5)

图1 布谷鸟算法流程图Fig.1 The schematic diagram of CS algorithm

可得，x到a的距离为|x-a|=x-a，根据式(5)可得x′到b的距离为|b-x′|=|b-(a+b-x)|=|a-x|=x-a，因此，这两个距离是相等的，如图2所示。

图2 任意实数与它的反向学习数Fig.2 A real number and its opposition based learning number

定义2反向点[12]，设X=(x1,x2,…,xD)为D维空间中的一点，xj∈[aj,bj]，其对应的反向点为：

(6)

由于可行解决方案和基于反向的解决方案位于搜索空间的两侧，因此当引入OBL策略时，可以扩大搜索区域并增强全局搜索能力。

2 DSCS算法

在DSCS算法中，引入了两个改进点。第一个是生成具有OBL策略的反向群体，并将其用于位置替换更新步骤中。第二个是在每一代结束时围绕当前全局最优解决方案深入寻找潜在的更好的解决方案。

2.1 反向学习策略

反向学习被RAHNAMAYAN等[10]证明了当前可行解的基于反向的解有50%的概率更接近全局最优解。虽然可行解决方案和基于反向的解决方案在相同条件下具有相同的概率保留给下一代，评估两者的解决方案，并选择更好的解决方案，它的生成算法能够提高获得最优解的概率。

本文在CS的搜索阶段，本文将levy飞行之后的目标函数值，与其在作用域范围内的反向解的目标函数和当前最优解的目标函数值进行比较，对最优解和当前最优解进行更新。通过反向学习减少搜索范围，从而提升解的搜索效率。具体步骤如下：

在反向学习策略中，设种群规模为N，维度为D，迭代过程选择更新位置时的位置矩阵为nestN×Di。每个维度的上下限分别为upN×Di，lowN×Di，则解的每维的基于反向学习的位置矩阵如下：

nestN×Di′=upN×Di+lowN×Di-nestN×Di

(7)

在DSCS中，产生的三个随机位置将会被反向群体nestN×Di选择，这种变化有效地扩大了搜索范围，并加快了全局最优解的搜索速度。

比较Levy飞行获得的解、Levy飞行获得的解的反向解以及当前最优解的目标函数值，本文将三个解中最小的目标函数值的解作为下一次迭代的最优解；蛋的位置更新，选择Levy飞行获得的解与Levy飞行获得的解的反向解中获得的位置更新。

2.2 逐维深度搜索

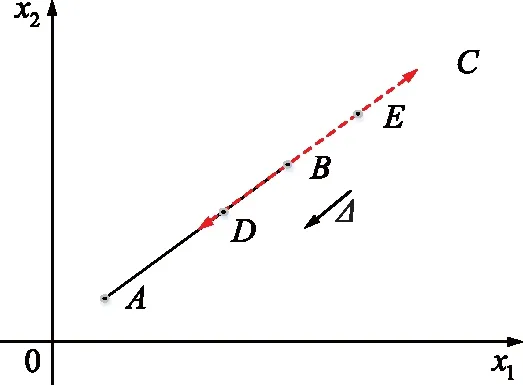
图3 A和B之间的位置关系Fig.3 Location relationship between A and B

步骤1对第i维的深度搜索：

1)计算A和B的坐标差：

XAB=XB-XA

(8)

2)计算局部搜索步长Δ：

Δ=ηXAB。

(9)

3)从位置B搜索可能更好的位置，对位置B做深度搜索有以下7个步骤：

①将搜索p设置为单位坐标;

②设置位置p的坐标Xp，则

XP=XB-p·Δ。

(10)

③分析位置p和当前的最优位置的目标函数值。如果位置p更小，则转到下一步，否则跳到步骤⑦。

④更新最优位置。

⑤比较位置p和B的目标函数值，如果位置p的目标函数值小，则用位置p代替B，转到下一步。

⑥如果p的值达到单向位置搜索最大数量Pmax，则转到下一步，返回步骤②。

⑦结束对当前位置的深度搜索。

步骤2判断当前维度是否为最后一维，若是对该蛋的最后一维更新，则对该蛋各维的深度搜索结束；否则更新该蛋的深度搜索维度：i=i+1，返回步骤1。

3 实验与结果分析

本节将DSCS与CS进行比较，以验证其有效性。实验平台是Windows7 MATLAB R2014b，5个测试函数如表1所示，F1—F3是单峰函数，F4—F5是多峰函数[14]。在实验过程中，DSCS和CS的参数如下：

固定参数：种群数量为N=30，个体维度D=20，每个维度的范围为[-20,20]，收敛精度δ=10-5，最大迭代次数tmax=5 000。

可变参数：被发现概率Pa=0.05，levy飞行的步长缩放因子α0=0.1；控制因素β=1.3。

DSCS参数：比例因子η=150，单向位置搜索最大数量Pmax=15。

每个实验分别运行30次，实验结果如表2所示。从表中可以看出，DSCS的性能相比CS算法，总体改善了解的质量，特别地，在F4函数上取得全局最优解。

表1 测试函数Tab.1 Test functions

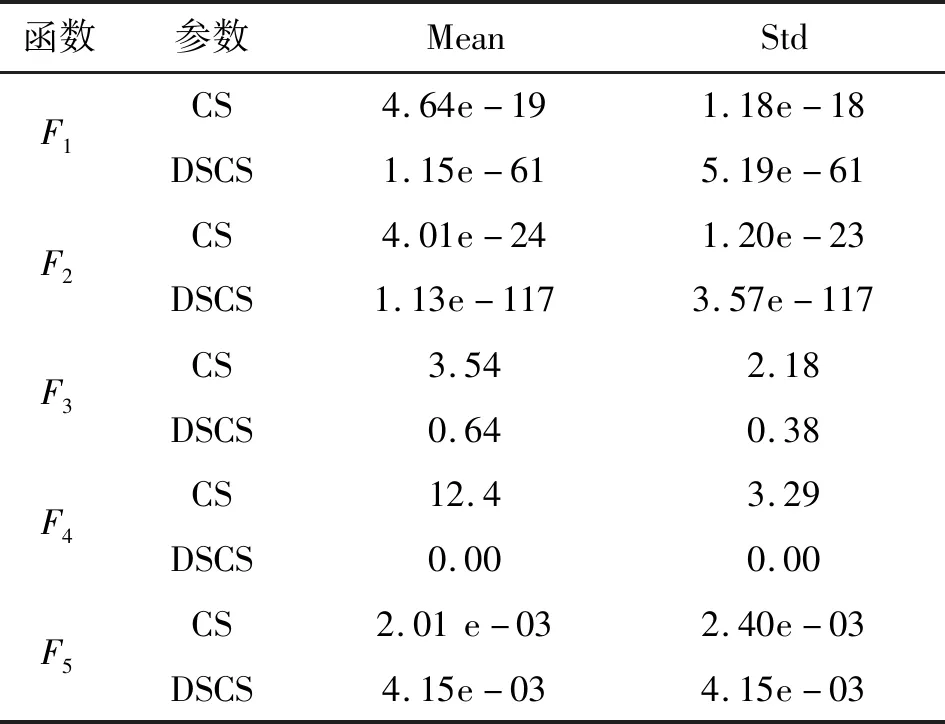
表2 DSCS和CS函数实验结果对比Tab.2 The optimization accuracy values of CS and DSCS

为了更好地观察改进算法的性能，实验设置算法结束条件为最大迭代次数，设置为5 000次，即tmax=5 000，其他参数保持不变。图4(a)～(e)以算法的迭代次数为横轴，适应度函数的对数值为竖轴，图形化的展示了改进算法和CS算法在5个测试函数中的寻优搜索收敛过程，其中，测试函数的维度为20。可以看出，无论测试函数是简单的单模函数还是复杂的多模函数，DSCS的收敛速度和收敛精度都高于CS的收敛速度和收敛精度。特别的，在函数F4和F5中，函数能够收敛到理论最优值，并且在函数的收敛过程中，相比较于CS算法，寻优收敛曲线斜率更小；因此，改进算法具有更好的后期搜索能力和更强的搜索活力。由此可得，本文改进的算法有效提高了CS算法的收敛精度和收敛速度。

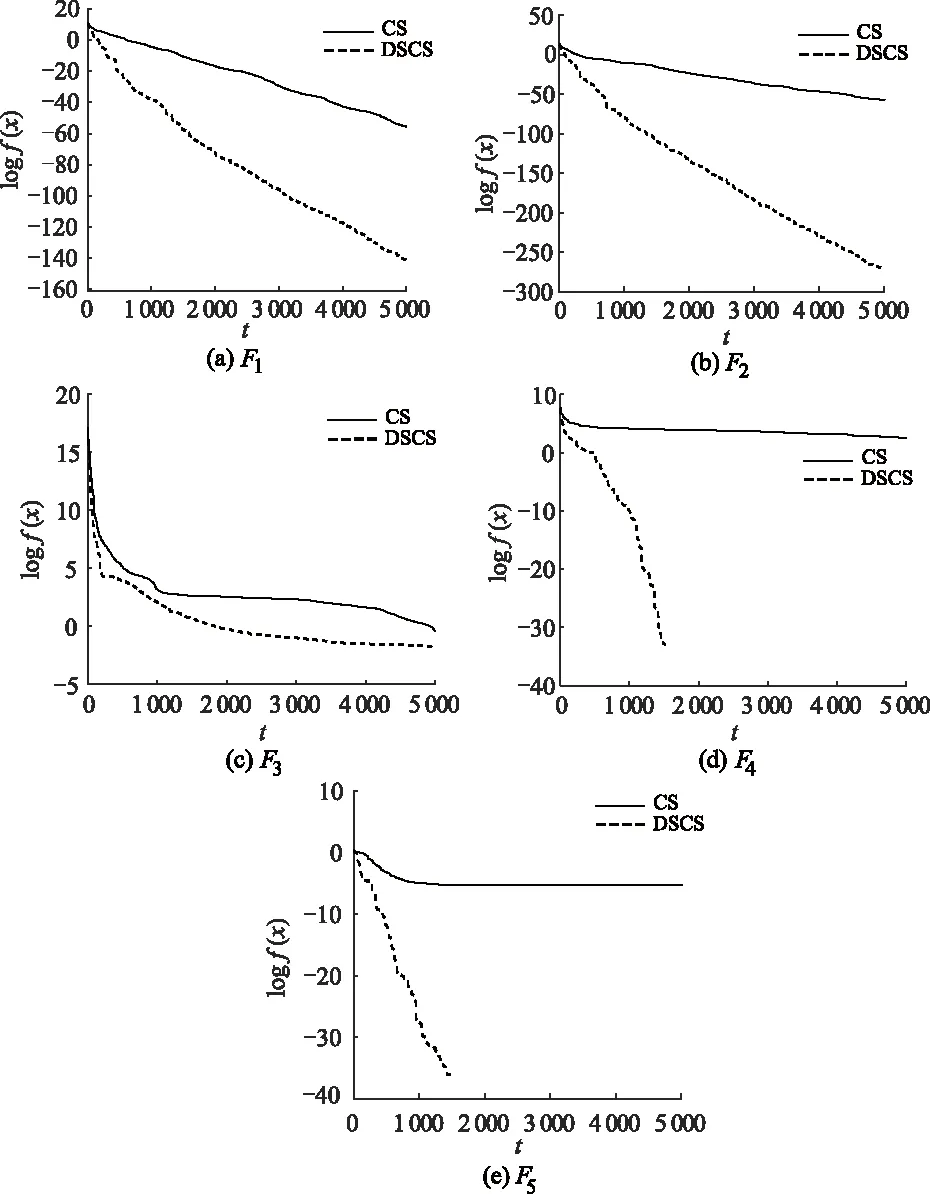
图4 DSCS与CS寻优收敛曲线图Fig.4 The optimization convergence curves of DSCS and CS

实验结果表明，针对本文选取的5个测试函数，本文提出的算法在引入基于反向学习策略和局部增强搜索操作后，算法的收敛速度，收敛精度和全局搜索能力都得到了不同程度的提高。

4 结语

在算法DSCS的选择阶段，基于初始化群体生成基于反向群体，然后随机选择三个新的个体替换初始化群体中丢弃的个体。在每一代的演化中，它类似于同时搜索两个对称区域，这加速了收敛速度并提高了全局搜索能力。对5种标准测试函数的实验表明，DSCS的性能明显优于CS。DSCS的全局搜索能力，收敛速度和收敛精度要好得多。对于简单的单模函数和复杂的多模态函数，DSCS在优化实验上表现出良好的鲁棒性。此外，本文的算法还需要在实际优化问题中进行分析验证，例如，应用于机器学习中的参数优化等。