“解题反思”在初中数学解题教学中的作用分析
2020-03-20朱村
朱 村
(江苏省苏州市胥江实验中学校 215004)
到底如何提高数学能力?死记硬背、题海战术都是不可取的方式.这些方式只会让学生对于题型进行熟悉或者了解,并不会对于其重点内容进行深刻的理解.当转换另一种题型变化的时候,学生依然会感到困惑.无论是死记硬背还是题海战术的方式,都只会让学生变成机械答题的机器人,而并不会让学生的数学能力得到真正的提高.因此,怎样提高数学能力的重点就在于让学生对于题型以及错题进行一定的反思.不仅反思自己错误的步骤,还要反思题型变化的应用.同时,教师还可以根据这样的方式引导学生培养自行主观能动力以及数学解题的反思能力.
一、初中数学解题过程的教学现状
在初中的数学教学过程中,教师对于学生的教学方式大多还存在于一些比较传统并且不灵活的现象.这样的现象表现在学生每日的作业都是繁复的习题以及公式,然而却只是进行机械化的解题,并没有根据重点题型进行理解.而教师对于学生在学习知识点后的错题只是进行了一些表面上的硬性要求.比如让学生准备错题本,但也只是通过反复摘抄,强化学生对于错题的印象而已.这样的方式并不能让学生真正地明白自身对于题型的错误方法,同时也会让学生对于数学习题的练习兴趣大大地减少和降低.
由于国家对于教育领域的大力推行,随着社会对于未来人才的吸收要求越来越高,在教育领域中出现了很多的创新模式,尤其是对于初中数学教学的课程改革.在这样的改革里,学生的学习压力会变得更大,同时所需要汲取的知识也会变得更加的繁多.而这也在初中数学教学的课堂当中出现了学生会左耳进,右耳出的现象.而这种现象也是导致学生不能良好地掌握数学解题的原因之一,最终造成一些极小的马虎和错误,难以去正确地解题.
二、解题反思对于初中数学教学的作用
1.解题反思的概念
解题反思是一种在初中数学学习中,开拓学生解题思路,提高学生解题能力的方法.它是通过让学生对一道题学习后进行一定的解题过程反思,从而达到反思一道题,学会一道题,反思一种题型,理解一种题型的效果.与其说它是一种学习方法,不如说它是一种能够帮助学生更好学习数学知识的一种良好习惯.在初中的数学解题教学中,这样的习惯不仅能够帮助学生激发对数学知识学习的兴趣,还能够培养学生们的反向解题思维并且最终提高学生的数学答题准确率.
2.初中数学教学中解题反思的应用
首先,教师必须要让学生在课前进行合理的预习学习.必要的预习会帮助学生简单地理解课程的基础内容重点,同时会对于重点进行自我的提炼,而在学习课程之后的解题过程当中就会通过这样的提炼重点进行正确并且有效的解题.
比如,在数学中学习分解因式的时候.
分解因式:a2-1+b2-2ab=____.
这道题的考点就是因式分解的分组分解法,老师可以让学生进行这样的思考:当被分解的式子是四项时,应考虑运用分组分解法进行分解.本题中a2+b2-2ab正好符合完全平方公式,应考虑为一组.
解a2-1+b2-2ab
=(a2+b2-2ab)-1
=(a-b)2-1
=(a-b+1)(a-b-1).
故答案为:(a-b+1)(a-b-1).
在做这道题的时候学生可以利用解题反思采用两两分组和三一分组的分解过程,最终选择正确的方式解题.
其次,教师可以创新自己的教学方式,利用情景式练习题让解题反思渗透到学生的解题过程当中.在这个解题过程当中,可以通过一些有趣的,生动的模拟情境,让学生充满对于解题的兴趣.而这样的教学方式在初中的数学教程中可以被很多次的利用到.
类似情景类的题库中有这样一道题:
题1某些植物发芽有这样一种规律:当年所发新芽第二年不发芽,老芽在以后每年都发芽.发芽规律见下表(设第一年前的新芽数为a)
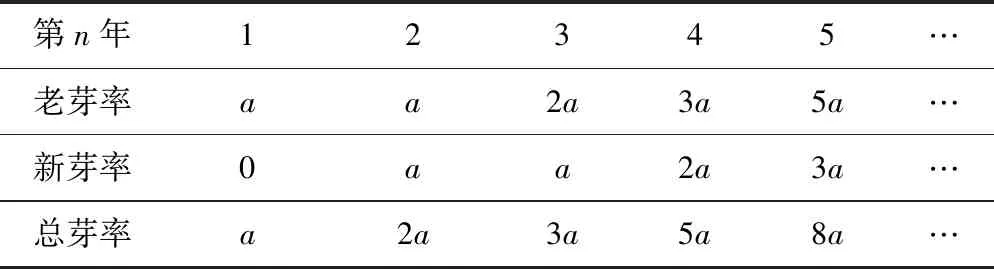
第n年12345…老芽率aa2a3a5a…新芽率0aa2a3a…总芽率a2a3a5a8a…
照这样下去,第8年老芽数与总芽数的比值为____(精确到0.001).
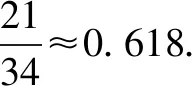
这道题的反思解题就必须要考虑到本题的关键规律:学生是否能够通过老芽数总是前面两个数的和这一规律,发现新芽数是对应的前一年的老芽数,而总芽数等于对应的新芽数和老芽数的和,在进行笔记摘录的时候对这种规律题也需要进行一定的标记.
而在对于抛物线的学习时,也要运用解题反思来学习.
题2已知抛物线y=-x2+2mx-m2+2的顶点A在第一象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与点A、B重合),过点C作CD⊥x轴于点D并交抛物线于点P.
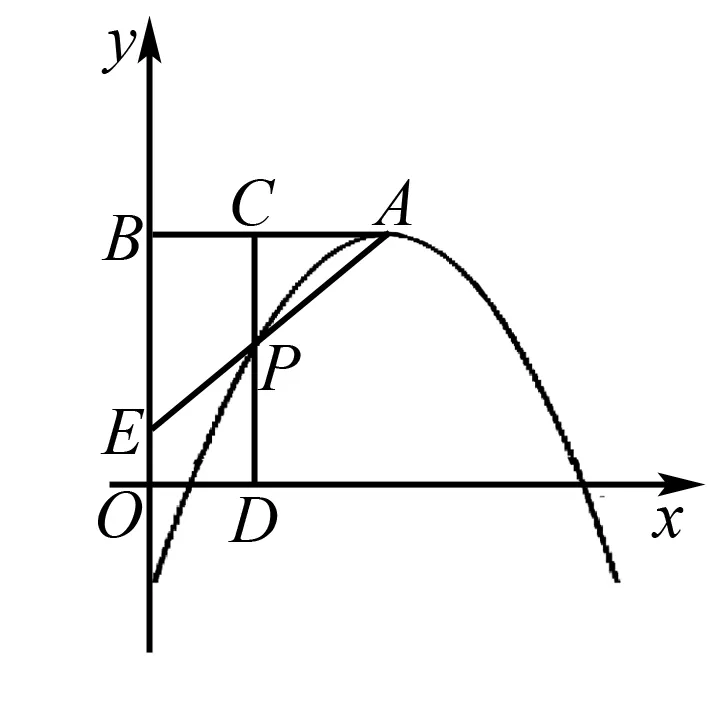
(1)若点C(1,a)是线段AB的中点,求点P的坐标;
(2)若直线AP交y轴的正半轴于点E,且AC=CP,求△OEP的面积S的取值范围.
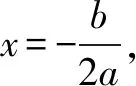
(2)把抛物线化为顶点式:y=-(x-m)2+2,可知A(m,2).设C(n,2),把n代入y=-(x-m)2+2得y=-(n-m)2+2,所以P(n,-(n-m)2+2).
∵AC=CP,
∴m-n=2+(m-n)2-2,即m-n=(m-n)2,
∴m-n=0或m-n=1.又∵C点不与端点A、B重合,
∴m≠n,即m-n=1,则A(m,2),P(m-1,1).
由AC=CP可得BE=AB.
∵OB=2,
∴OE=2-m.
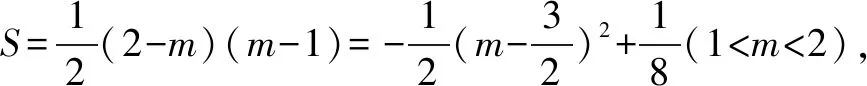
在学生对于这一题型进行错误解题之后,教师要通过让学生反思自己解题过程中思路以及解题规律,从而进行题型的重点归纳,让学生彻底地理解这一题型的考核重点.
最后,需要教师对于学生进行一定的加强训练,教师可以通过让学生准备专门的解题反思错题本.区别于以前的表面摘抄,教师需要让学生将题型进行归类和知识重点挑拣,同时将具有代表性的错题摘录在题型下方,并且对于当时的解题思路进行一定的反思解题过程.尽量在这个过程中要包含自己的反思过程,以及正确的解题思路.这样可以让学生在不同系列题型中清楚地看到题型的解题问题和方法.在初中的数学教学解题过程中,教师还可以培养学生的存异心理.切记千万不能将正确的解题思路一味地灌输给学生,要让学生产生不同的话语和思路,从而进行自我的解题思路校正.这样也可以让学生的解题能力大大提高,同时还可以培养良好的解题反思的习惯.
初中数学对于学生的培养目的是在于创造学生的思维逻辑以及创新方式.在新课改之后,初中数学更是要求学生具有抽象以及具象的双重思维能力,教师不能忽略学生的解题技能发展,同时也不能忽略学生对于数学知识的兴趣产生,需要通过培养学生解题反思的良好习惯来去解决课堂学习效果不显著的状况.通过教师对于解题反思的教导,以及合理的设置教学方案,学生将会大大提高自身思维逻辑能力以及对于知识提炼重点的能力.而这也是教师们引导学生进步的目标所在.
