一元一次不等式(组)的运用对策(提优篇)
2020-03-20宋扬
宋 扬
(江苏省扬州市田家炳实验中学 225000)
有许多不等式,本身并不是一元一次的,但往往都可以化为一元一次不等式(组)来求解. 诸如二次不等式、分式不等式、绝对值不等式,等等.另一方面,不等式(组)与数学其他知识点的综合运用也随处可见. 解决问题的总体对策是实施转化,转化的关键是找到相应的理论根据,使之在变形过程中保持同解性不变.
一、用于解二次不等式
类型对策:通常先将不等式右边化为0,左边分解为两个一次因式的乘积,然后逆向使用两实数相乘的符号法则,把二次不等式转化为两个一次不等式组,分别求解后,再综合起来.
注:(1)上述方法的适用范围:不等式化为一般形式后,左边的二次式有两个实根的情形.对于没有实根的情形,可作适当处理,以确定其解的情况(或为无解,或解为一切实数).
(2)解一元二次不等式,通用方法是图象法(借助二次函数的图象求解).
例1 解不等式x2+2x<15.
解移项、分解因式得(x-3)(x+5)<0,于是有

由不等式组①得 无解;由不等式组②得 -5 所以原不等式的解集为 -5 要点指导:(1)本题逆用两实数相乘的符号法则具体是指:两数相乘若得负,则两数异号. 显然,其中包括两种情况. (2)例1解题完成后,可将不等式中的“<”,依次改为“≤”、“>”、“≥”,分别看一看各自的求解过程和结果,以能掌握这部分内容的全面情况. 类型对策1:通常先将不等式右边化为0,左边化为一个分式(这里是指两个一次式相除的形式),然后逆用两实数相除的符号法则,把分式不等式转化为两个一次不等式组,分别求解后,再综合起来. 注:与前述解二次不等式的理论依据、方法相一致,有异曲同工之妙!想一想,相同点和不同点各有哪些? 类型对策2:若分式不等式的右边是一个常数,左边是一个分式,可直接对左边的分母按正、负两种情况分类讨论,把分式不等式转化为两个(一次)不等式组,分别求解后,再综合起来. 所以原不等式的解集为x>3或x<-5. 要点指导:(1)本题逆用相除的符号法则是指:两数相除,若得正,则两数同号;若得负,则两数异号. (2)将本题与例1的求解过程和结果相对照(按“>”、“<”、“≥”、“≤”分别对照),有什么发现?对这部分内容,可做个总结,以能总揽全局. 解法2 对原不等式分两种情况讨论,再加以综合. 综上可知,原不等式的解集为x>3或x<-5. 要点指导:特别要注意,此题切切不可直接将原不等式两边同乘(x+5).想一想,为什么? 类型对策1:关键是怎样化去绝对值符号.通用方法是分类讨论.其一般步骤是:以各绝对值(内)的零点为分界点,把变量的取值依次分段,然后逐段求解,最后加以综合.逐段求解时,都是依据绝对值的基本性质:当a≥0时,|a|=a;当a<0时,|a|=-a. 先正确写出去掉绝对值符号后的式子(这里指一次不等式),然后求解. 类型对策2:对于只有一个绝对值符号的不等式,可根据绝对值的定义(即绝对值的几何意义),直接写出去掉绝对值符号后的式子,继而求解. 使用这种方法的主要情形有两种:设f(x)是代数式,a是一个正实数. (1)若|f(x)| 类型对策3:作同解变形. 比如,满足一定条件时,可将不等式两边同时平方,注意到|f(x)|2=[f(x)]2. 解法1 先分两种情况各自求解,再综合. 要点指导:依据绝对值的定义分类讨论,然后综合. 要点指导:(1)依据绝对值的几何意义化去绝对值符号;(2)这种连写的不等式,实质上也是不等式组,只是书写形式不同而已;(3)直接解连写的不等式容易出错. 要同时考虑“三边”(或“多边”),而不是两边. 为了避免差错,对稍复杂的连写不等式,还是转换成不等式组的形式后再求解为宜. 类型对策:多用于带参数的方程(组)求满足某种特定条件的解(解集),或以此来确定参数的取值(或范围). 通常先把参数看成常数,求出方程(组)的解,然后根据限制条件列出相应的关于参数的不等式(组),并求其解集,得到参数的取值(或范围). 若题中还有其他求解目标,则根据条件继续求解. 例4 当且仅当k为何值时,方程组 由(*)式又可知,当且仅当k取整数时,原方程组有整数解.故当k=2,3,4时,原方程组有正整数解. 类型对策:常用于求函数的最值等相关问题. 关键是列出关于自变量的不等式(组),然后求其解集,就是相应函数的定义域. 随之,问题便迎刃而解. 例5 非负实数a、b、c满足3a+2b+c=5,2a+b-3c=1.设y=3a+b-7c,求y的最大值与最小值之和. 要点指导:本题的a、b、c具有同等地位,其中任一个都可选作自变量. 类型对策:关键在于针对需要求解的问题,列出合适的不等式(组). 除了根据给出的已知条件(显性条件),还常常用到相关几何图形本身的基本概念(定义)和性质. 隐含条件的使用,也往往具有选择性. 例6 一个三角形的三边长分别为xcm,(x+3)cm,(x+6)cm,它的周长不超过30cm,求x的取值范围. 要点指导:隐含条件当用则用,不可或缺. 本题的隐含条件是三角形任意两边之和大于第三边,应选择两小边之和大于第三边.二、用于解分式不等式



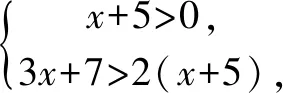
三、用于解绝对值不等式
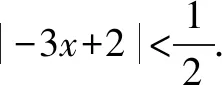

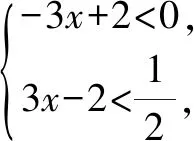


四、与方程(组)的综合运用


五、与函数的综合运用

六、与几何问题的综合运用

