基于GA的碰撞参数优化研究

程洋洋，魏志芳，刘森林，黄书伟，刘伊华

(1.中北大学 机电工程学院，山西 太原 030051；2.中国兵器工业第208研究所，北京 102202)

在自动武器中，碰撞是传递能量的常见工作方式。其中曲线槽与凸笋的碰撞过程中，影响碰撞过程中反跳速度的因素有很多。目前，国内外学者对于碰撞问题的研究大多是将参与碰撞的物体都视为刚体，没有考虑其材料属性，假设碰撞过程瞬间完成，不考虑碰撞过程中的作用时间[1]，只能得出 构件碰撞前后的速度，无法得到碰撞过程中碰撞速度与材料参数之间的关系，没有从更深的角度去解释碰撞现象的物理本质。在接触力学仿真分析中[2]，机构间的碰撞参数难以进行准确设置，难以保证其动力学仿真精度。因此有必要开展自动武器冲击碰撞动力学精确建模技术的研究。文献[3]中通过实验来研究碰撞特性，探究了恢复系数对碰撞的影响；文献[4]中基于ADAMS进行碰撞分析，研究了刚度、步长和积分器对于仿真精度的影响；文献[5]中运用Impact函数对碰撞反跳速度进行了研究。

自动武器的碰撞仿真常采用ADAMS进行仿真，因此参数的设置至关重要。针对ADAMS Impact函数中接触碰撞参数和ANSYS Workbench中材料参数进行仿真分析，采用单一辨识构建参数间的非线性映射关系，利用Isight的多岛遗传算法建立目标函数并进行优化，为提高仿真精度提出了一种行之有效的方案。

1 动力学建模

1.1 建立假设模型

自动武器曲线槽与凸笋碰撞属于曲面-平面碰撞，关系到自动武器后坐复进，影响武器射击性能。为了简化计算，便于研究，以球-板模型为研究对象，代替曲线槽与凸笋的曲面-平面碰撞，如图1所示。假设球-板均为柔体，质量为m的球体从距板高L=0.1 m处自由落体，与平板碰撞后自由反弹。

为提高计算效率，在对仿真结果不造成影响的前提下对该碰撞模型进行适当调整：将球体从静止自由落体到碰撞前一刻的运动过程进行简化，从球体和平板发生碰撞前的一瞬间开始仿真，根据自由落体，可得球体碰撞前瞬时速度为1 400.47 mm/s，钢与钢恢复系数为0.56，因此计算得球体碰撞后瞬时速度为784.26 mm/s.

1.2 灵敏度分析

灵敏度分析是分析输入变量对仿真结果的影响程度，分别以接触碰撞参数与材料性能参数作为输入，以反跳速度作为输出进行分析。通过大量仿真得到如下结果。

1.2.1 ADAMS接触碰撞参数

ADAMS中采用碰撞函数模型进行仿真，其中接触碰撞参数包括接触刚度K、刚度指数e、接触阻尼c和穿透深度p.接触刚度通常使用Hertz接触碰撞模型近似计算；刚度指数反映了材料的非线性程度，金属与金属材料推荐值为1.5；接触阻尼反映了碰撞过程的能量损失；穿透深度的增加会使接触阻尼增大。

在ADAMS中创建设计变量，对接触碰撞参数依次代入，施加约束并求解，得到碰撞后反跳速度随接触碰撞参数变化曲线，如图2～5所示。

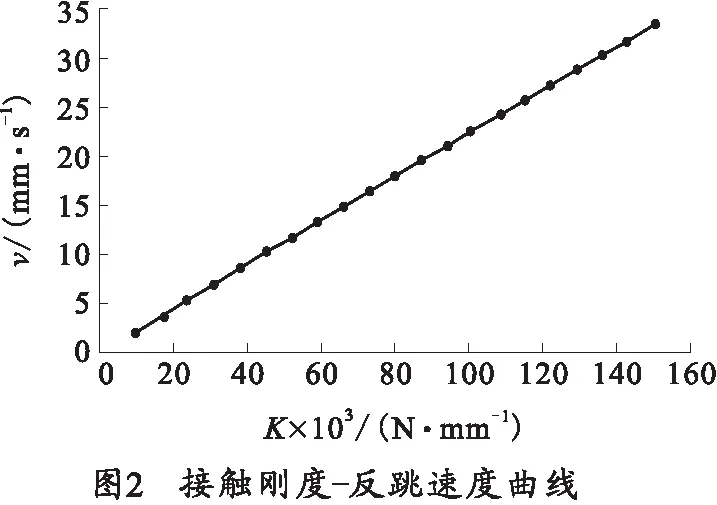
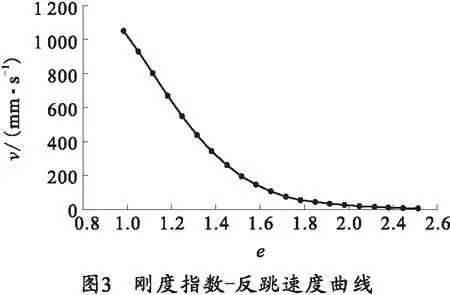
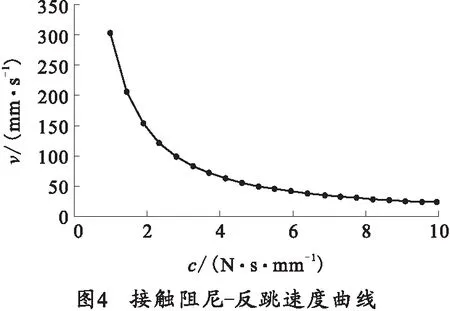
由图2～5可知，反跳速度与接触碰撞参数中接触刚度正相关，且随着接触刚度与穿透深度增大而增大、随着刚度指数和接触阻尼增大而减小。

1.2.2 ANSYS Workbench材料性能参数

机构间碰撞接触分析属于冲击碰撞动力学问题，可使用Workbench自带瞬态动力学模块Tran-sient structural进行分析。在材料设置中，选取材料性能参数弹性模量E、泊松比μ、屈服强度σs作为影响因素进行分析。根据机械设计手册常用金属材料的弹性模量和泊松比范围[6]，可确定其取值范围分别为E∈[10，310]GPa、μ∈[0.2，0.4]、σs∈[205，380] MPa.

在Workbench中，通过划分网格、施加载荷约束后进行求解，得到碰撞后反跳速度随材料性能参数变化曲线，如图6～8所示。

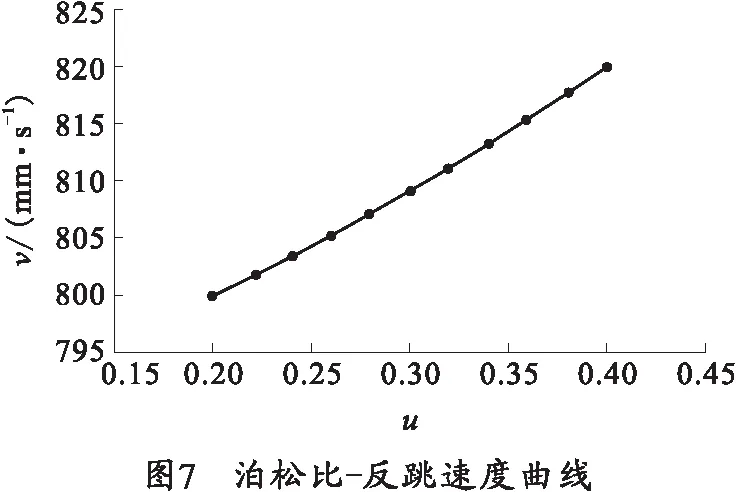
分析图6、7的仿真结果可知，反跳速度随弹性模量增大而减小，随泊松比增大而增大。但从数据中分析可知，泊松比取值范围[0.2，0.4]内，反跳速度变化范围为[800.06，819.79] mm/s，变化程度为2.47%.因此，泊松比在一定取值范围内，反跳速度对泊松比变化不敏感。

从图8可以看出，反跳速度对屈服强度变化不敏感。

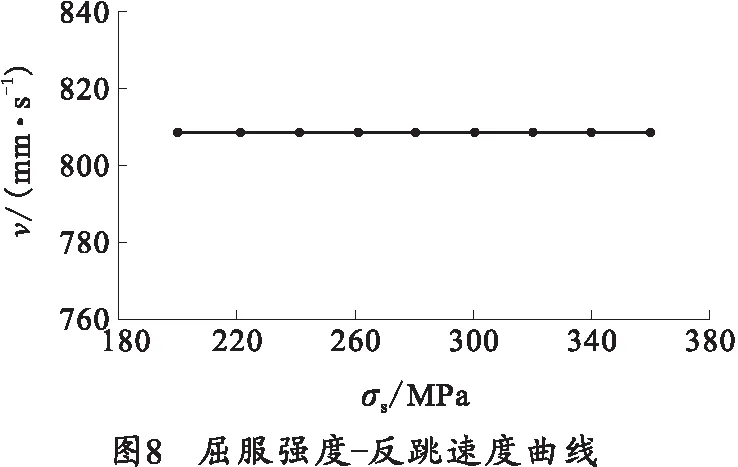
通过上述分析，接触碰撞参数对反跳速度影响较大，而材料性能参数中屈服强度与泊松比对于反跳速度影响很小，故只考虑弹性模量对于反跳速度的影响。因此，可将接触碰撞参数与材料性能参数间非线性映射考虑为接触碰撞参数与弹性模量间的非线性映射关系。

2 基于遗传算法的参数优化

接触碰撞参数与材料性能参数之间有着复杂的关系，笔者将通过参数辨识拟合出接触碰撞参数与反跳速度、材料性能参数与反跳速度的函数关系，根据此函数形式假设函数关系式并建立目标函数，利用遗传算法进行求解优化。

2.1 单一参数辨识

动力学系统辨识是典型的“灰箱问题”。笔者通过ADAMS中自带的试验设计模块Insight可进行DOE参数辨识，该模块可考虑多个变量同时变化时，各设计变量对虚拟样机性能的影响，以区别关键参数和非关键参数。

接触碰撞参数取值范围及初始值根据材料属性及ADAMS软件推荐值确定，K取值范围为[10 000，150 000]；e取值范围为[1.0，2.5]；c取值范围为[1，10]；p取值范围为[0.01，0.10].

进行DOE分析时，创建目标函数作为仿真结果优劣的评判指标。通过理论计算分析，已知碰撞后反跳速度最大值为784.26 mm/s，则创建试验目标为(min(ABS(.model.MEA_z_velocity-784.26)).

各参数取值范围和初值如表1所示。

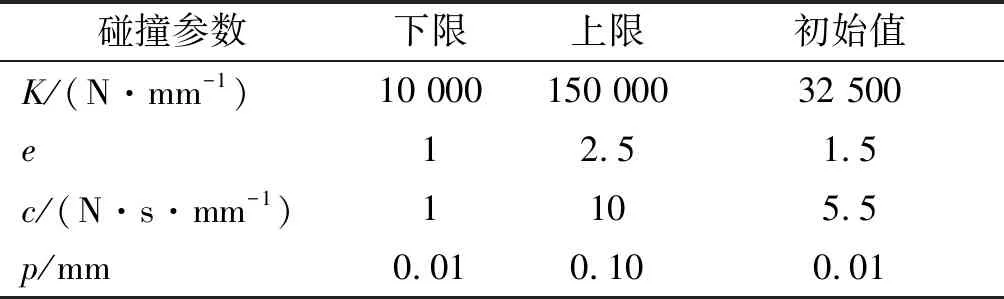
表1 设计变量取值范围

根据上述目标函数与设计变量取值，采用一次响应的近似模型，创建全因子法设计矩阵，定义625次迭代，得出接触碰撞参数与反跳速度相对映射关系，各接触参数影响大小如图9所示。

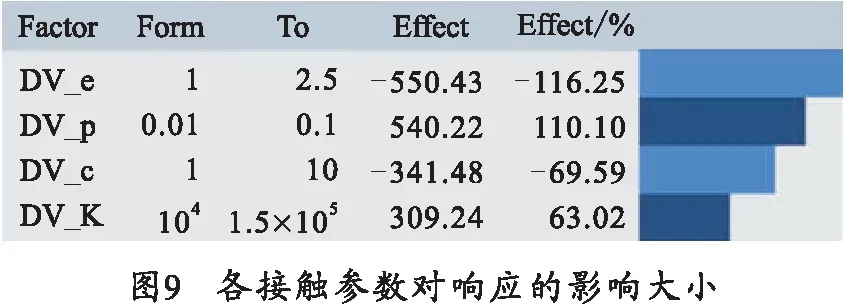
由图9可知，参数中对响应影响最大的是刚度指数e，其次是穿透深度p、接触阻尼c和接触刚度K.

根据迭代结果分析，辨识出的碰撞参数有多种情况，没有唯一解，只有相对最优解，取满足目标函数的相对最优碰撞参数辨识结果，如表2所示。

表2 碰撞参数DOE辨识结果

通过使用表2中DOE辨识值仿真得出反跳速度为774.484 mm/s，与理论值784.26 mm/s比较，相对误差为1.2%，精度满足工程设计要求。

2.2 假设函数关系式

利用MATLAB对球体-平板碰撞动力学及ANSYS workbench瞬态动力学仿真分析的结果数据进行曲线拟合。

1)对图6中的反跳速度值与弹性模量E之间的关系数据进行拟合，得到材料参数(弹性模量)与反跳速度之间的函数关系式。拟合结果为

v(E)=0.001 006E2-0.903 1E+945.3.

(1)

2)对图2中的反跳速度值与接触刚度K之间的关系数据进行拟合，得到接触碰撞参数(接触刚度)与反跳速度之间的函数关系式。拟合结果为

K(v)=4 478v-768.7.

(2)

3)同理得到e，c，p与反跳速度之间的函数关系式：

e(v)=0.874 3e-0.021 97v+1.72e-0.000 562v,

(3)

c(v)=137.7v-0.838 8-0.117 8,

(4)

p(v)=0.019 59v0.552 3.

(5)

为了进一步优化函数关系，提高仿真精度，根据单一辨识拟合出的接触碰撞参数与反跳速度的映射关系形式,假设函数关系式如下：

(6)

2.3 基于遗传算法的优化

利用Isight多岛遗传优化算法[7-8]，以反跳速度为目标函数，以目标函数接近理论计算值为目标，在约束条件与设计变量取值范围内计算，得到如表3的碰撞函数系数的优化结果。

分析表3中的优化值，将优化值代入到式(6)中，得到优化的接触碰撞参数与反跳速度的关系式，结合碰撞后反跳速度与材料参数(弹性模量)之间的函数关系式(1)，将式(1)代入到优化后接触碰撞参数与反跳速度的关系式，得到优化后的接触碰撞参数与材料性能参数(即弹性模量)之间的非线性映射关系，优化结果为：

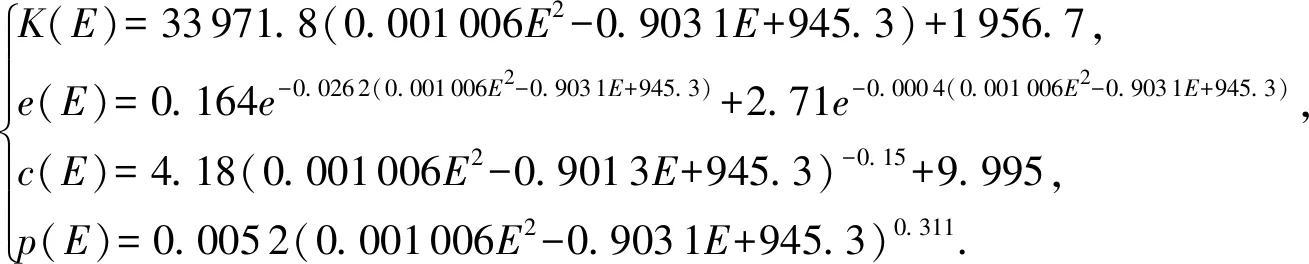
(7)

3 优化结果验证仿真

设碰撞模型采用材料为普通碳素结构钢Q235B，其弹性模量为210 GPa，通过式(7)辨识接触碰撞参数K，e，c，p分别为2.664 5 N·mm-1，1.982 5，11 N·s·mm-1，0.042 mm，并代入仿真模型进行验证，得到碰撞分离速度曲线，如图10所示。

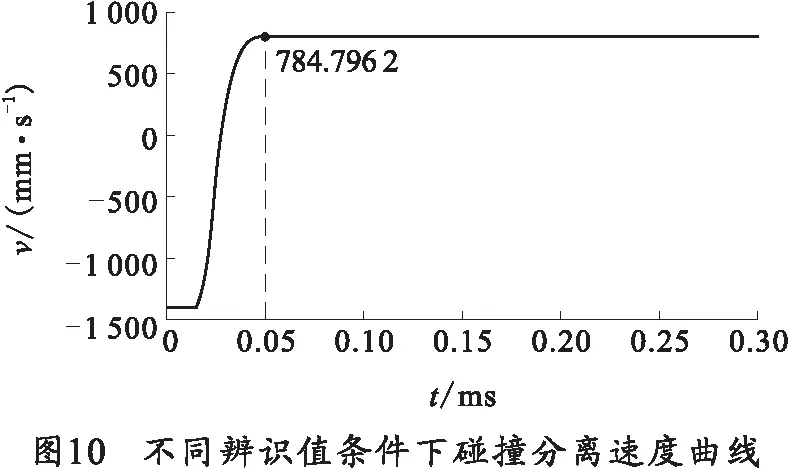
将不同辨识值下反跳速度最大值与理论计算值进行分析，结果如表4所示。

表4 仿真结果与理论值对比情况

分析表4可以得出，采用遗传算法进行函数系数优化，优化后目标函数明显提高，达到根据材料参数进行动力学仿真的参数设置优化目的。此外，遗传算法与理论值吻合很好，相对误差小于1%，表明优化结果具有较高的可信度。

4 结论

笔者基于大量的球-板模型仿真结果，通过对其进行参数辨识、推导函数关系、遗传算法优化等一系列分析，可以得出以下结论：

1)材料性能参数中，反跳速度对泊松比和屈服强度的变化不敏感；而反跳速度随着弹性模量增大而减小；接触碰撞参数对反跳速度均有影响。

2)基于遗传算法可以有效求解目标函数，得到优化结果，且采用优化后的接触碰撞参数进行仿真，与理论值高度吻合，可见该方法效果很好。