基于胞元拓扑优化法的内凹六边形负泊松比超材料结构设计
2022-04-26康小方柳景超夏光辉许庆虎
康小方,柳景超,夏光辉,3,4,许庆虎,3,4
(1.安徽建筑大学 土木工程学院,安徽 合肥 230601;2.智能地下探测技术重点实验室,安徽 合肥 230601;3.安徽省BIM 工程中心,安徽 合肥 230601;4.安徽省装配式建筑研究院,安徽 合肥 230601)
泊松比是用作材料的泊松比效应的度量系数,泊松比也被称作材料的横向变形系数,材料在力作用与力作用垂直方向上的横向变形特性。泊松比是指材料在受力加载方向下,其横向应变与纵向应变比值的相反数[1-3]。生活中所使用的材料泊松比取值一般不小于0,常见的金属泊松比一般在0.3左右。液体是一种极为致密的材料且不可被压缩,在压力的作用下体积几乎没有变化,其泊松比接近0.5。
约160 年前,经典弹性理论提出了材料出现负泊松比的可能性[4]。常见的内凹结构包括内凹六边形、双箭头模型、星型和手性等结构。1982年,Gibson 等[5]首次提出了内凹六边形蜂窝模型;Yang S 等[6]提出了一种矩形穿孔的负泊松比结构。采用拓扑优化方法设计负泊松比超材料为超材料结构优化设计提供了一种新的途径,该方法已广泛应用于负泊松比超材料结构优化[7-8]。
负泊松材料主要类型有[9]:①天然负泊松比材料;②胞状负泊松比材料;③金属负泊松比材料;④由多种普通基材所组成的多重负泊松比材料;⑤由负泊松比材料和非负泊松比材料复合形成的负泊松比复合材料。
与传统泊松比材料相比,负泊松比超材料几乎具有两倍的抗断裂性[10-12],具有负泊松比效应的复合材料抗断裂性也大约是传统复合材料的两倍。桥梁的伸缩缝材料要求其性能满足垂直和平行于桥梁轴线的两个方向都可以自由变形。然而,负泊松比超材料具有受到压力时横向收缩、受到拉力时横向膨胀的特性。负泊松比超材料安装在梁体间隙之中拥有足够的变形能力,同时负泊松比效应还能够对材料的横向和竖向承载能力有一定的增强。随着负泊松比超材料结构的快速发展,已经涉及到人工假体[13]、智能传感器[14-16]、纺织类材料、分子过滤器[17]、减震器[18]、隔声器[19]和防护垫[20]等领域。1989 年,Bendsoe[21]采用微结构[22]的拓扑优化法对结构进行拓扑优化。
本文将微结构的设计转换成了胞元拓扑优化设计,采用胞元拓扑优化法对内凹六边形微结构进行拓扑优化,将优化得到的胞元微结构按一定周期进行排列从而获得负泊松比超材料结构。
1 内凹六边形负泊松材料计算理论
1.1 负泊松比材料作用机理
泊松比是衡量材料在承受纵向力时的横向尺寸变化力学参数。负泊松比是在考虑正负应变的前提下,横向应变和纵向应变的比值相反数,其数学表达式为,
式中,εx,εz分别为横向应变和纵向应变;Δx,Δz分别为结构受荷后的横向变形和纵向变形。一般情况下,泊松比大小和材料内部结构相关,经典弹性力学理论证明了具有各向同性的材料其泊松比值范围为-1.0 ~0.5[23]。从泊松比取值范围上来看,材料具有负泊松比效应理论上是可行的。
1.2 内凹六边形拓扑优化
本文从材料(微观尺度)到结构(宏观尺度)进行研究。所采用的方法是在保持宏观材料分布不变的前提下,对微观尺度材料下单胞结构进行拓扑优化设计。将优化得到的胞元微结构按一定周期进行排列从而获得负泊松比超材料结构。如图1 所示:
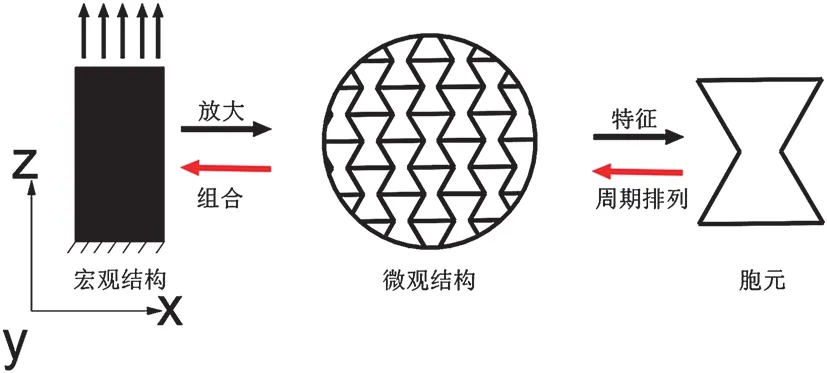
图1 微观-宏观-一体化
内凹六边形源自常规六边形结构,但是其两侧呈内凹结构,其中:a 为底部边长,b 为斜边长,c 为肋部边长,a,c 为常量;θ0为初始角(< 90°)。如图2 所示:
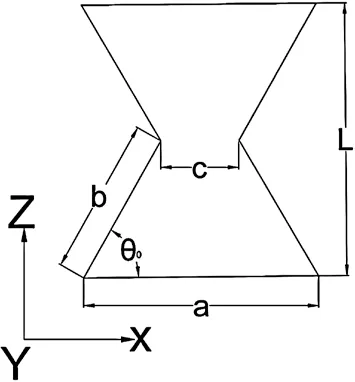
图2 内凹六边形结构胞元示意图
根据负泊松比定义和内凹六边形结构图,负泊松比可表示为,

根据几何分析,横向应变εa可表示为,

式中,θ0,θ和分别为胞元结构的初始角度和变形后角度。
由图2 可知胞元结构尺寸b,a,c 和初始角度θ0之间的关系可表述为,

于是,胞元结构的泊松比v为[24],
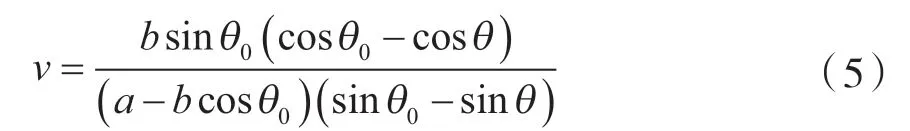
由式(4)代入式(5)可得下式,
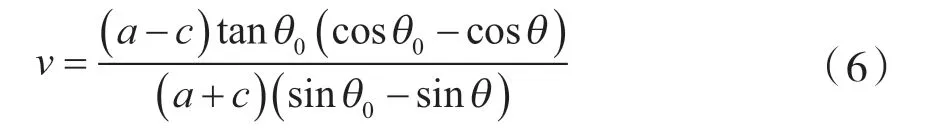
采用Matlab 软件对式(3)和式(6)进行计算,可得胞元结构的横向应变εa(图3)和泊松比v(图4)。
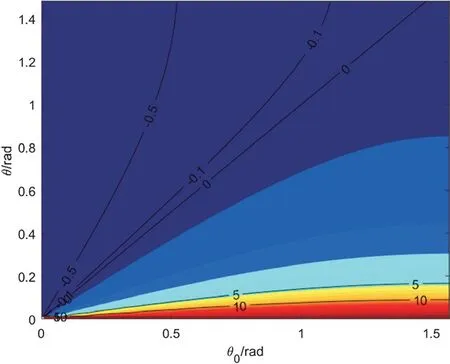
图3 结构胞元横向应变εa 等高线
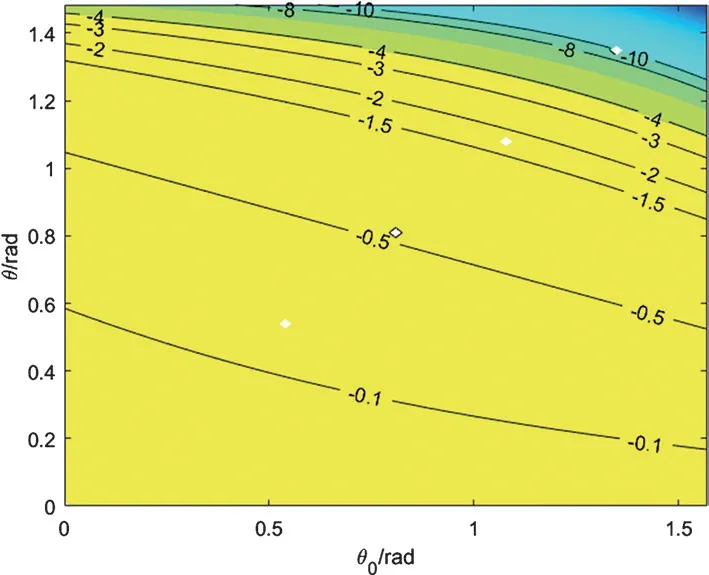
图4 结构胞元泊松比v 等高线
具有负泊松比效应的内凹六边形拓扑优化步骤可表述为:
(1)通过图1 所示的微观-宏观一体化优化思路,将宏观结构看作由一系列内凹六边形结构胞元(图2)所组成。
(2)对内凹六边形结构胞元进行结构优化,通过改变图2 所示的初始角θ0,来实现结构胞元的负泊松比效应。
(3)根据步骤(2)获得的负泊松比效应结构胞元,按一定周期进行排列组成负泊松比超材料结构。
(4)根据步骤(3)获得的负泊松比超材料结构,采用ANSYS 有限元软件建立相应的结构模型。
2 内凹六边形胞元结构力学行为
为验证基于胞元拓扑优化法的内凹六边形负泊松比超材料结构受力性能,本节采用大型有限元软件ANSYS 进行建模,对优化后的结构胞元进行受力分析和泊松比验证。本文建立代表性内凹六边形结构胞元,假定结构胞元尺寸a 和c 为常量,初始角度θ0为变量,结构胞元尺寸a=3 mm,c=1 mm,初始角度θ0=30°、45°和60°,材料弹性模量为1.2×105MPa,材料泊松比为0.29。
为了保证结构胞元可以两端受拉,利用作用力与反作用力的关系将结构胞元边界条件定为下端固定约束,胞元上端施加5 MPa 大小的拉应力。
2.1 初始角度θ0=30°内凹六边形
结构胞元的纵向尺寸z=1.155 mm,x=3 mm。结构胞元经加荷载后,其纵向变形为Δz=-0.445 51 mm,结构胞元的横向变形Δx=-0.195 148 mm。将有限元仿真结果代入公式(1)可以得到材料的泊松比,泊松比=-0.167 9。
2.2 初始角度θ0=45°内凹六边形
结构胞元初始角度θ0=45°,其纵向尺寸z=2 mm,x=3 mm。经加荷载后,结构胞元的纵向变形为Δz=-0.634 55 mm,结构胞元的横向变形Δx=-0.511 254 mm。将有限元仿真结果代入公式(1)可以得到材料的泊松比,泊松比v=-0.537 1。
2.3 初始角度θ0=60°内凹六边形
结构胞元初始角度θ0=60°,结构胞元的纵向尺寸z=3.464 mm,x=3 mm。在加载荷载后,其纵向变形为Δz=-0.717 286 mm,结构胞元的横向变形Δx=-0.554 977 mm。将有限元仿真结果代入公式(1)可以得到材料的泊松比,泊松比v=-1.492 36。
由图5 ~图10 可知,随着结构胞元初始角度的增大,内凹六边形结构胞元负泊松比值也越大。
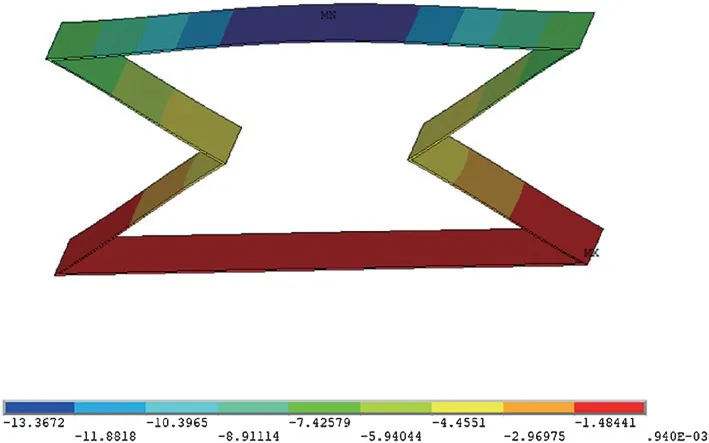
图5 θ0=30°Z 方向变形图
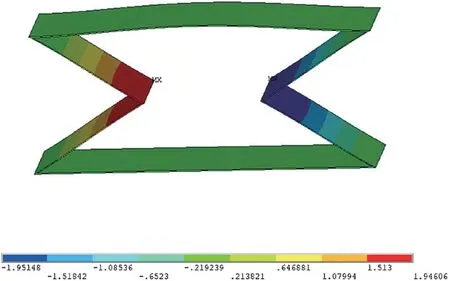
图6 θ0=30°X 方向变形图
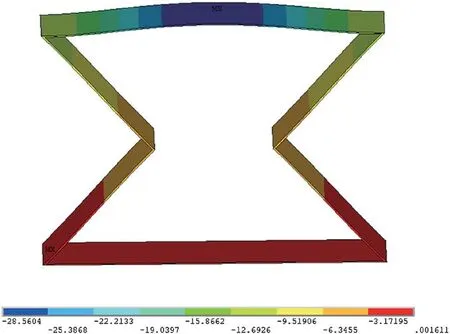
图7 θ0=45°Z 方向变形图
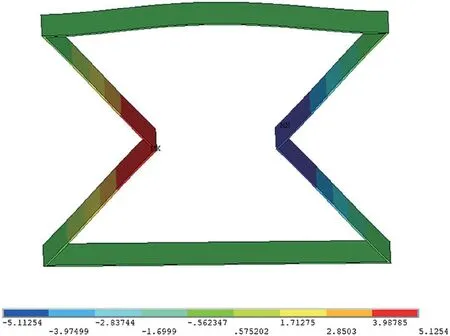
图8 θ0=45°X 方向变形图
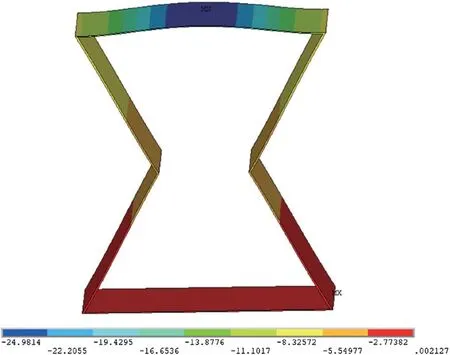
图9 θ0=60°Z 方向变形图
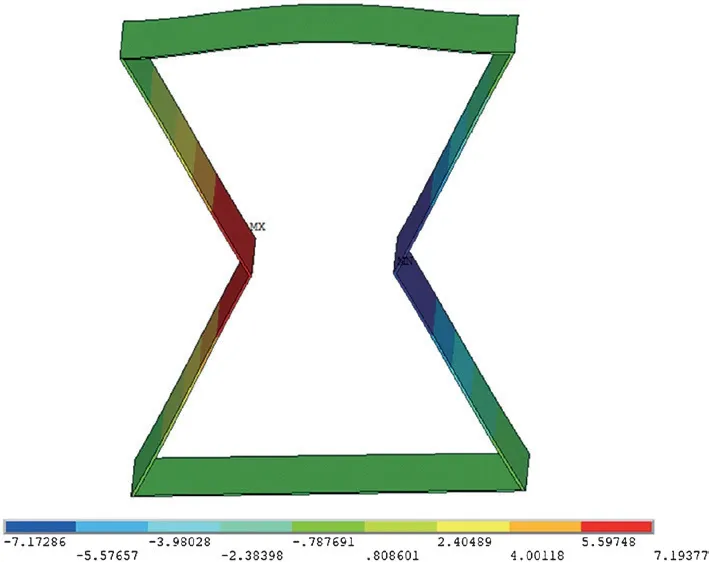
图10 θ0=60°X 方向变形图
为验证有限元模型的准确性,将受荷情况下结构胞元的负泊松比效应和理论公式进行对比。根据结构胞元尺寸a=3,c=1,初始角度θ0=30°、45°和60°,分别代入式(6)可得v30°=-0.168 6、v45°=-0.505 0、v60°=-1.517 5,将有限元仿真结果和理论计算结果进行汇总,可得泊松比值如表1 所示:

表1 泊松比值
将有限元计算的结果与理论计算的结果进行比对,发现误差均在10%以内,从侧面反映出有限元仿真的准确性及负泊松比理论计算的合理性。
3 内凹六边形超材料结构性能仿真
3.1 内凹六边形超材料宏观结构阵列
为分析材料拓扑优化后的超材料结构宏观力学性能,本文将经过拓扑优化后的第3 节内凹六边形按一定周期进行排列得到相应具有宏观负泊松比效应的超材料结构。如图11 所示:
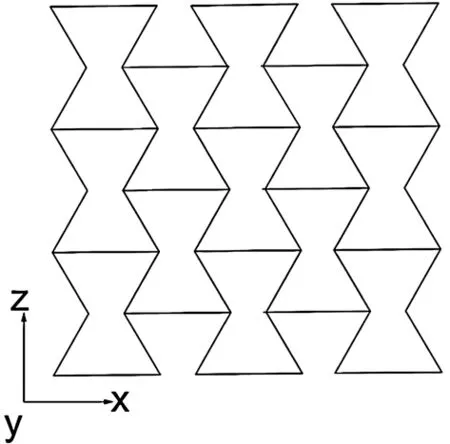
图11 内凹六边形宏观结构阵列示意图
3.2 内凹六边形超材料结构有限元仿真
根据图9 所示,结构胞元按照一定的规则进行排列,可获得相应的超材料结构。采用有限元软件ANSYS 进行建模仿真,超材料结构边界条件为下端固定约束,胞元上端施加5 MPa 大小的拉应力。
3.2.1 初始角度θ0=30°超材料结构
由一系列初始角度θ0=30°的结构胞元组成的超材料结构,其纵向尺寸z=3.462 mm,横向尺寸x=11 mm。经加荷载后,超材料结构的纵向变形为Δz=-0.380 01 mm,超材料结构的横向变形Δx=-0.136 8 mm。经公式(1)计算可得超材料结构的泊松比v=-0.113。
3.2.2 初始角度θ0=45°超材料结构
根据初始角度θ0=45°的结构胞元,经过一定的排列规律组成宏观超材料结构,其纵向尺寸z=6 mm,横向尺寸x=11 mm。经加荷载后,超材料结构的纵向变形为Δz=-1.13555 mm,超材料结构的横向变形Δx=-0.598 61 mm。经公式(1)计算可得超材料结构的泊松比v=-0.288。
3.2.3 初始角度θ0=60°超材料结构
采用初始角度θ0=60°的结构胞元,经组合成超材料结构,其纵向尺寸z=6.928 mm,横向尺寸x=11 mm。经加荷载后,超材料结构的纵向变形为Δz=-1.538 47 mm,超材料结构的横向变形Δx=-1.299 89 mm。经公式(1)计算可得超材料结构的泊松比v=-0.532。
由图12~图17 可得,内凹六边形超材料结构的负泊松比效应跟结构胞元特性有关。随着结构胞元初始角度增大,超材料结构的负泊松比值也越大,其变化规律与结构胞元负泊松比效应类似。
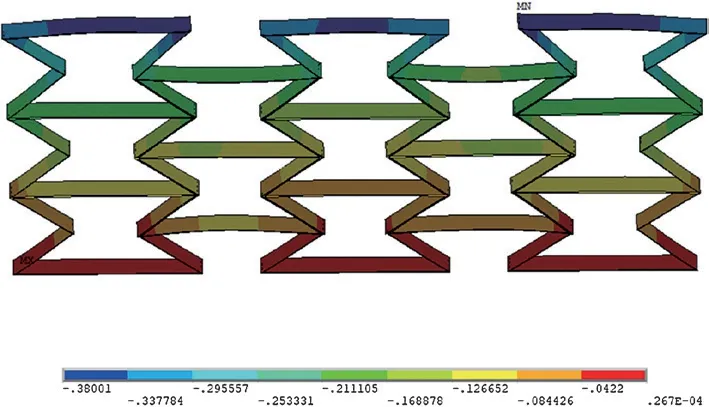
图12 =30°Z 方向变形图

图13 =30°X 方向变形图
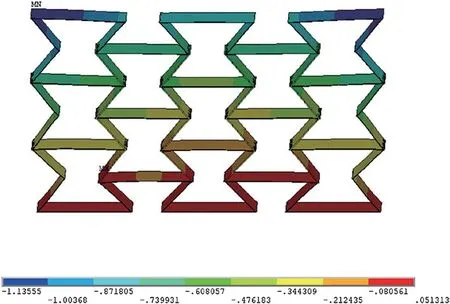
图14 =45°Z 方向变形图
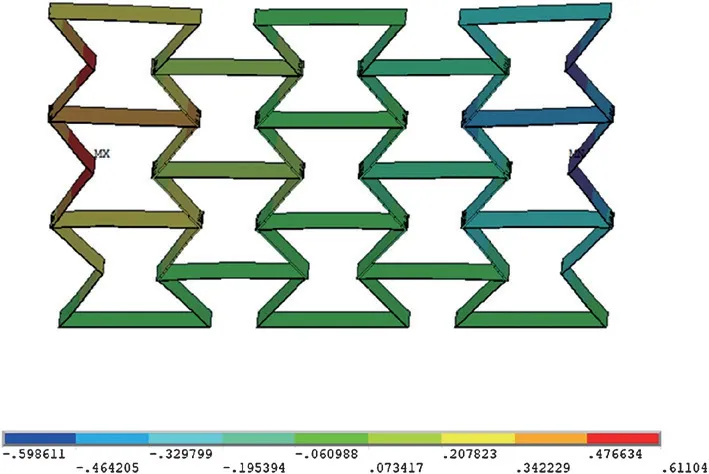
图15 =45°X 方向变形图
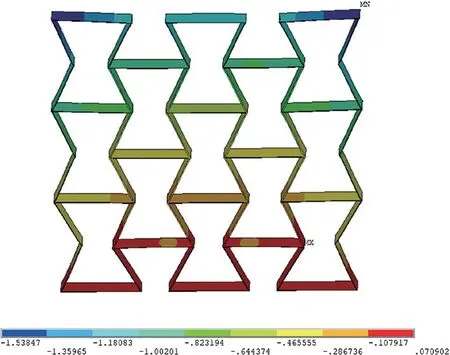
图16 =60°Z 方向变形图

图17 =60°X 方向变形图
4 结论
本文采用胞元拓扑优化的方法,以超材料负泊松比效应增强为目的,推导得出了内凹角越大其负泊松比效应越强的理论,并应用有限元软件ANSYS 对其进行仿真,结果表明:
(1)基于胞元拓扑优化的方法,得到内凹六边形负泊松比超材料在底边长和纵向长度保持不变时,内凹角越大其负泊松比效应越为明显。并且结构胞元按一定周期进行排列的宏观结构的负泊松比效应和结构胞元的负泊松效应改变规律保持一致。
(2)相较于传统的对结构胞元的形状进行改变来达到拓扑优化的结果,本文采取了对内凹六边形初始角度进行改变,将负泊松比效应与内凹六边形的角度用函数关系关联了起来,更为有效地确定了负泊松比效应与形状的具体关系。
(3)内凹六边形胞元按一定周期排列后整体结构的负泊松比效应将略有减小,在其受到纵向拉(压)应力时,其横向将会发生膨胀(收缩)变形。桥梁伸缩缝要求其在垂直和平行于桥梁的轴线上都能自由变形,这种负泊松比结构较为符合其需求。拓扑优化可以得到大量的负泊松比超材料结构,对负泊松比超材料结构的获取和强化有着极为重要的作用。
