考虑弹性的导弹倾斜发射动力学研究

2020-03-20周晓和袁天元南宫自军

火炮发射与控制学报 2020年1期

王亮，张妍，周晓和，袁天元，南宫自军

(中国运载火箭技术研究院，北京 100076)

陆基战术导弹在采用导轨倾斜发射时，发射安全性和导弹控制系统启控是两个关键环节。前者需关注导弹离轨过程中，需要导弹离轨过程中导弹姿态不能发生较大改变，避免与发射系统发生碰撞，确保导弹顺利发射离轨，因此导弹在飞离安全区域前，控制系统不能启动控制；后者需关注导弹离轨后导弹姿态的变化，尤其是初始静不稳定的导弹，其在无控情况下会姿态逐渐发散，因此需要尽快起控，纠正姿态。可以看出，这两者的设计关心的时间段和内容是不一样的，且有时是矛盾的，发射安全性希望启控时间靠后，而导弹初始起控希望启控时间靠前，如何权衡需要系统设计和考虑。

导弹发射过程的研究是学术界的研究热点和难点，研究主要集中在发射过程对发射平台、发射场坪的影响研究，以及对发射过程运动过程的研究。

针对发射过程对发射平台、发射场坪的影响研究，杨春浩等[1]基于最优拉丁超立方(OLHD)试验设计方法和径向基神经网络近似技术，建立了带有塑性损伤本构关系的无依托发射场坪的近似模型；对场坪位移动态响应的各影响因素进行了敏感度分析。周晓和等[2]采用Hongnestad方程及改进后的Saenz单轴方程分别拟合混凝土在受压时的上升段及下降段应力-应变关系，构建了一条适用于沥青混凝土的受压应力-应变曲线。黄韬等[3]基于ABAQUS大型有限元软件，采用塑性损伤本构建立发射场坪非线性精确数值有限元模型，分析了导弹发射状态下的动态响应。战仁军等[4]以武警无人战车为例，建立了车体系统的四自由度模型，分析了车载武器的振动模态，推导了系统对后坐力冲击的振动响应函数，对比了不同发射角度的系统振动响应。

针对发射过程运动过程的研究，孙船斌等[5]基于发射平台系统结构建立了全行程刚度突变的多级油缸等效力学模型和考虑预压量的适配器动摩擦力学模型，对车身进行柔性处理，建立了考虑场坪坡度的六自由度1/2冷发射平台弹射动力学物理模型和振动方程。何连珠等[6]通过对复合材料机翼部件的动特性及动响应分析，比较了外翼、中翼和内翼3种发射导弹的计算情况，给出最严重情况的动力响应值，最后确定其动强度。朱怀亮等[7]采用有限元方法模拟柔性旋转火箭的空间运动姿态，建立变截面转轴的动力学偏微分方程，给出发射过程中火箭动态响应的数值解。林永明等[8]把多体系统动力学的Kane方法和有限元法应用于火箭柔性发射系统。针对工程实际，对建模与求解过程中的一些关键问题进行了探讨。

综上所述，学术界对导弹发射过程的刚体运动研究较多，但是一方面建立的模型缺少考虑起飞过程的气动力的影响和弹性响应，因此无法考虑导弹在离轨时刻由于变形释放产生的动载荷;另一方面缺少研究导弹及发射参数对离轨过程的影响。因此，建立较为完善的刚体-柔性体发射动力学模型，并且研究各参数对离轨过程的影响，对指导导弹发射动力学设计有重要意义。针对该问题，笔者研究了刚柔耦合的导弹倾斜发射动力学模型，考虑了离轨时刻导弹弹性变形释放产生的弹性响应和动载荷，以及离轨后低速飞行过程中的气动力。

1 导弹倾斜发射的运动方程

假定导弹在离开发射车安全距离前，空气舵等操纵机构不动作，且重型导弹一般采用前后滑块同时离轨的方案。考虑如图1所示的导弹，导弹为正常布局。弹长为l，发射时起竖角为α，导弹受到发动机推力为F和前后滑块的支撑力作用。在发射过程中，由于水平地面风w、刚体的沉浮运动Z(向下为正)、俯仰运动θ(低头为正)和导弹的弹性振动y的影响，导弹第i分站产生附加攻角Δαwi，而生成附加升力ΔLwi.

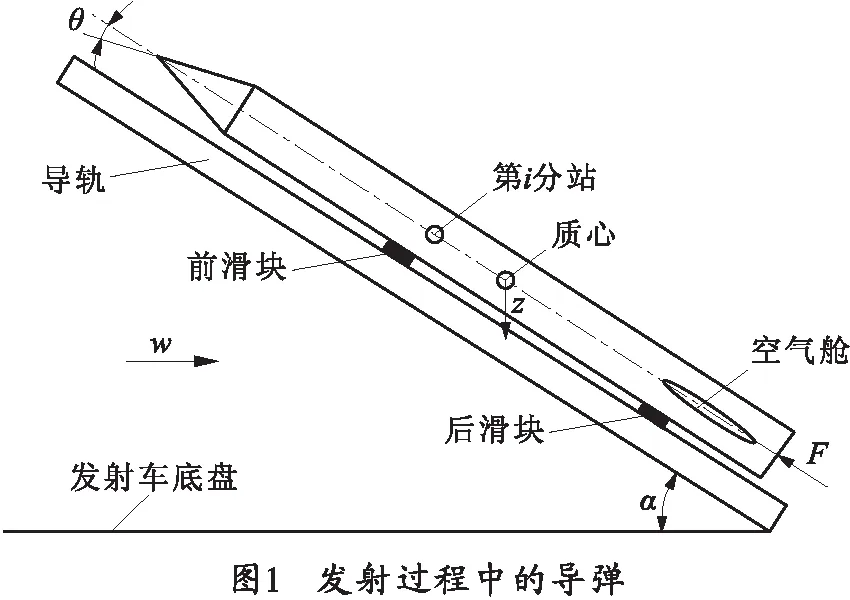
各分站附加攻角Δαwi不仅需要考虑导弹在垂向的运动和导弹俯仰姿态的改变，另外还需要考虑地面风作用以及弹体的弹性响应。计算公式如下所示：

(1)

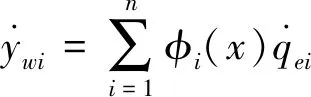
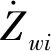
(2)

式中：Zc为质心处沉浮位移；xg为导弹质心坐标。

各分站的附加升力ΔLwi计算公式为

(3)

考虑弹体结构动力学前i阶模态，导弹轴向运动由于与横法向解耦在此不考虑，因此导弹离轨后的增量平衡方程可以表示为

(4)

式中：m和Iy分别为导弹质量与绕质心的转动惯量；mri、cri和kri分别为导弹第i阶模态质量、阻尼和刚度。

将式(1)～(3)带入式(4)，考虑导弹一阶弹性模态后，整理可以得到：

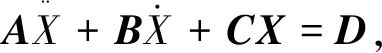
(5)

式中各项表达式为：

2 导弹结构动力学模型

笔者按照文献[9]的建模方法，采用梁-质量块模型建立导弹的结构动力学模型。首先将导弹分成若干分站，各分站上的质量以集中质量单元连接在各节点上。由于导弹为连续气动外形，沿弹长方向各处的截面形状不相等，因此梁单元采用了变截面的铁木辛克梁模型，采用形如式(6)的方法计算获得。根据振动理论，在飞行过程中阵风引起的一阶弹性振动载荷，剪力Q与弯矩M的计算公式如式(7)所示,式中参数具体含义见文献[9].

(6)

(7)

3 算例

3.1 方法的可行性研究

根据弹道特征数据，选择导弹离轨时刻开展计算，研究该方法的可行性。

导弹弹长约6.5 m，质量约3 300 kg，转动惯量约10 000 kg·m2.根据导弹动力学参数，可以得到导弹该飞行时刻一阶模态频率为21 Hz，另外选择导弹一阶阻尼比为0.01.

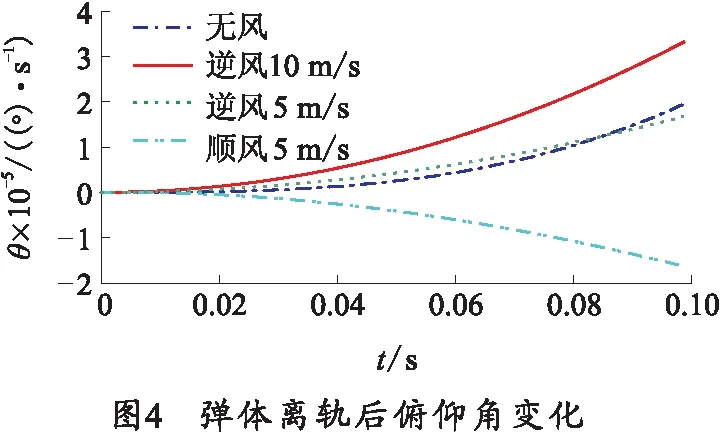
导弹在满足离轨一定安全距离后控制系统才会启动控制，笔者研究离轨后、起控前的过程，因此仅给出导弹离轨后的无控刚体运动、自由弹性响应以及产生的弹体动载荷。设定发射角度为60°，导弹离轨时刻飞行速度20 m/s，地面风为从顺风5 m/s变化到逆风10 m/s.将导弹相关参数带入式(5)，可以计算得到该导弹弹尖处的位移振动响应和刚体运动响应曲线,如图2～4所示。

另外,根据位移振动响应计算出导弹离轨后的弹体动载荷，如图5、6所示。

通过分析可以发现：

1)弹性响应方面，导弹离轨前，弹体在重力和前后滑块支撑力作用下发生弹性变形，在离轨时刻由于导弹在前后滑块支撑下产生的弹性变形瞬时释放，产生弹性响应，弹体受到动载荷。导弹弹性响应呈现自由衰减特性，最大位移响应以及最大动载荷发生在离轨时刻，后续由于弹体阻尼的作用逐步衰减，算例中最大位移响应达到7 mm左右，最大动剪力和动弯矩约为1 kN和2.5 kN·m.因此,一方面实际导弹离轨过程中由于弹性释放产生的变形可能会影响离轨安全性，需要关注发射净空的设计；另一方面离轨时刻的弹性响应产生的动载荷较大，因此需要关注离轨时刻导弹弹体载荷和强度的设计。

2)刚体运动方面，在离轨时刻具备一定的速度，导弹受到重力、气动力作用下，由于气动力较小，导弹在重力作用下产生向下沉浮运动，离轨0.1 s时达到了25 mm；同时，导弹绕质心产生低头俯仰运动。由于该刚体运动为发散型运动，因此在设计时需要关注刚体运动对发射净空的影响，另外需要联合控制设计和发射动力学开展发射起控设计，在确保发射安全性的同时可稳定起控飞行。

3)地面风的影响方面，由于导弹自重较大，气动升力作用可以忽略，因此地面风对导弹沉浮运动影响较小；地面风对俯仰运动有一定的影响，由于逆风作用产生了低头力矩，使得导弹低头趋势加快，而顺风作用正好相反，甚至在有些情况下会使导弹抬头。导弹在地面风的作用下的俯仰运动需要多关注，尤其是地面发射时的低速大攻角气动特性与发射动力学联合分析。

3.2 导弹参数对运动和响应的影响

在发射动力学研究时，可能更加关注导弹各参数对运动和响应的影响，找出最大影响因素，在设计时予以重点关注。

为研究导弹各项参数对刚体运动和弹性响应的影响，给出规律性结果,选择了导弹质量、转动惯量和发射角度这3个参数，研究其对发射过程的影响，并设置了3种工况进行研究：

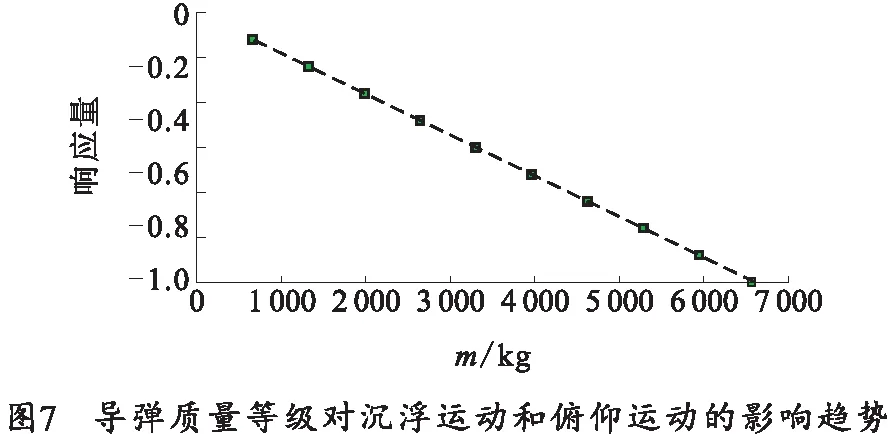
工况1：导弹质量从500 kg变化到7 000 kg，转动惯量跟随变化，发射角度保持60°不变。此工况下，导弹质量等级对沉浮运动和俯仰运动的影响趋势一致，对刚体运动的影响基本呈现线性趋势，导弹质量越重，沉浮运动和俯仰运动响应越大。典型的沉浮运动在离轨后同一时刻的响应值如图7所示。

工况2：导弹质量不变，调整长细比，转动惯量从4 000 kg·m2变化到17 000 kg·m2，发射角度保持60°不变。此工况下，导弹惯量等级对沉浮运动和俯仰运动的影响趋势一致，基本呈现非线性趋势，随着导弹惯量变大，沉浮运动和俯仰运动响应值变大，且变化率先变大后变小。典型的俯仰运动在离轨后同一时刻的响应值如图8所示。

工况3：导弹参数不变，调整发射角度从20°到80°.此工况下，发射角度对导弹的沉浮运动、俯仰运动以及弹性响应的影响基本一致，均为随着发射角度的增大，响应呈现非线性减小的趋势，且变化率先变大后变小。这是由于随着发射角度的增加，导弹重力在导弹横法向的分量越小，导弹离轨前的弹性变形变小，因此对导弹的影响越小。典型的俯仰运动趋势如图9所示。