接触电阻对电磁轨道炮电磁场影响分析

刘 畅，刘 峰，刘新民

(燕山大学 河北省重型装备与大型结构力学可靠性重点实验室，河北 秦皇岛 066004)

电磁轨道发射是一种利用电磁能驱动电枢滑动至超高速的发射技术，在未来军事领域具有广泛的应用前景[1]。电枢高速发射过程中，电枢与导轨之间的接触面需要承载兆安数量级以上的高脉冲电流[2-4]。然而，滑动接触的接触面即使精抛光，但对于电接触也是粗糙的，电流通过面上相互接触的高点或粗糙的点，即a斑点，从而构成接触电阻。a斑点的数目和半径的大小都与接触压力成一定程度的正比关系，即接触压力越大a斑点数目越多，a斑点的半径越大[5]。为了达到电流均匀分布的目的，通过调整电枢结构形式和尺寸关系使得尾部接触力稍微小于接触前部，a斑点密度与前部接触压力大的区域相当，减小电流集中。因此研究接触电阻对发射性能和效率的影响有着重要意义[6-7]。Hsieh等建立了电接触效应的三维有限元模型，并给出了接触电阻率关于接触压强、接触中较软材料的硬度和试验模型的平均电阻率的关系[8-10]；陈允等[11]进行了在充电电压和放电时序相同的条件下，进行了3种不同材料的发射试验，分析了枢轨间滑动电接触特性；朱仁贵等[12]进行了多组不同电流线密度的重复发射实验，分析了滑动接触电阻和接触面焦耳热耗散的变化规律；袁瑞敏等[13]进行了不同充电电压但放电时序相同的发射试验，分析了枢轨间接触电阻的动态特性；李鹤等[14]进行了电磁轨道炮发射试验，并结合实验数据计算发射过程中的回路阻抗和接触电阻。由此可见，现阶段已通过试验得到枢轨接触面的接触电阻特性，但通过数值模拟来观察接触电阻对电枢发射的影响却很少，所以笔者对考虑接触电阻影响下电磁轨道发射进行电磁场分析。

1 有限元模型

根据文献[8-10]计算不同接触压力下的接触电阻率：

(1)

式中：ρc为接触电阻率；ρa为接触体的平均电阻率；wc为接触层厚度；Hsoft为较软接触体的硬度；PCPRESS为接触压力；m和c1为经验系数。

为计算枢轨接触面的接触电阻，需计算枢轨接触面的接触压力。其中在Maxwell中铝和铜的电导率分别为38 MS/m和58 MS/m，则ρa取两者的平均值；m和c1的取值根据文献[8-10]中所给出，铜和铝相互接触的情况下c1=9.45×10-4；m=0.63.

为了保证电枢和导轨间接触良好，电枢和导轨间使用过盈接触[15-18]，电枢与轨道尺寸如图1所示。

由于枢轨接触压力分布不均，为模拟枢轨间接触电阻，需将枢轨接触表面进行区域划分和薄层处理，薄层厚度设置为0.5 mm，接触电阻区域处理根据枢轨间过盈产生的接触压力分布进行划分。在接触压力分布较为集中的区域,划分需要更加精确。枢轨接触表面长25 mm，除5～15 mm处每2 mm划分为1个区域外，其他部分皆为5 mm划分为1个区域，划分后的电枢如图2所示。

电磁轨道发射装置简化模型一般由储能装置、电源调节装置、两平行导轨和导轨间紧密接触的电枢组成。电源激励在Maxwell瞬态场中利用Maxwell Circuit Editor设计单一电容激励电路提供脉冲电流，如图3所示。其中电容容量为40 mF，二极管电阻参数为3 Ω，初始电压为20 kV，电感线圈电感系数为2 μH.

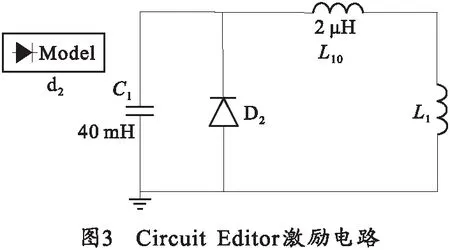
通过Maxwell的电磁场分析，得到0～2 ms电枢发射过程中垂直于导轨方向不同时刻的洛伦兹力大小。通过外力加载的方式，加载到Workbench模型中的对应区域上，并在Workbench中计算枢轨接触面的接触压力。其中电枢尺寸与Maxwell中电枢尺寸唯一区别在于，在Workbench结构场计算中增加了0.25 mm的过盈尺寸。计算得到的接触压力即为考虑洛伦兹力下的接触压力，再将接触压力计算成接触电阻带入到Maxwell中进行电磁场分析，将结果与理想接触下的电磁场分析进行对比，讨论接触电阻对于电磁发射的影响。

2 结果及分析

2.1 接触电阻分析

计算得到的接触电阻变化曲线如图4所示。

由图4可以看出，改变接触电阻后回路电流略小于理想接触下的回路电流。根据电流曲线可以将接触电阻的变化分为3个阶段：0-A段为电枢的启动段，电枢滑动很短一段距离，而枢轨间的接触突然变为滑动接触，枢轨间接触压力分布不均匀，集中分布在电枢中间位置，而电枢前末端皆与导轨不接触，将未接触区域设置为电导率为0，则计算接触电阻时不计算在内。而当电枢运动一段之后，枢轨接触面积急剧增加，而接触压力增加较为缓慢，局部接触电阻率虽略有减小，但接触区域的变化从而导致接触面积和接触长度的变化，因此接触电阻急剧增加；而当电流增大，接触压力急剧增加，接触区域无较大变化，因此接触电阻急剧减小；A-B段为电枢的高加速段，电流逐渐增大到峰值，从而使枢轨间接触面积逐渐增大，接触电阻逐渐减小；B-C段为电枢低加速段，随着电流的逐渐减小，枢轨间接触压力也逐渐减小，微观接触斑点减少，于是接触电阻逐渐增加。

2.2 电磁场分析

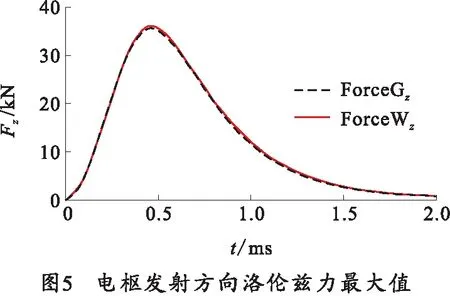
图5、6中ForceG和ForceW分别为考虑接触电阻下和理想接触下电枢沿发射方向洛伦兹力和垂直于导轨方向的洛伦兹力曲线。

由图中可以看出，考虑接触电阻的电枢沿发射方向的洛伦兹力最大值略小于理想接触下的洛伦兹力最大值，且考虑接触电阻下的电枢在垂直于导轨方向的洛伦兹力最大值小于理想接触下的电枢。

考虑到洛伦兹力与电流密度成正比，所以分别观察枢轨接触表面和电枢喉部的最大电流密度，如图7、8所示。图中J_G和J_W分别为考虑接触电阻下和理想接触下枢轨接触面的最大电流密度。

从图7、8中可以看出，由于枢轨接触表面由于接触电阻的增大，考虑接触电阻影响下的电枢喉部最大电流密度小于理想接触状态下的电枢喉部最大电流密度；考虑接触电阻后枢轨接触表面最大电流密度低于理想接触状态下枢轨接触表面最大电流密度，这也和图6的洛伦兹力曲线相符合。

由于电流密度的峰值出现在0.3 ms，而电流的峰值出现在0.5 ms，故分别取0.1、0.3、0.5、1.2 ms 4个时刻各截面电流密度云图作为比较。图9、10分别为理想接触状态下和考虑接触电阻下的电枢喉部截面电流密度图。

观察图9的电流密度分布，由于感应电动势和霍尔效应，电流密度最大值出现在电枢喉部内侧的棱角处，在0.1、0.3和0.5 ms时刻电流密度最大值分别为4.85、6.61和4.85 GA/m2.当电流急剧下降，电枢喉部中感应磁场在中心区域感应出最大电动势，而产生的感应电流阻碍电流的减小，所以电流密度在电枢喉部中心区域集中，而在边缘区域电流密度较小。对比图10电流密度分布可以看出，改变接触电阻后电枢喉部电流密度虽略有减小，但电流密度分布的区域基本一致。

图11、12是分别为理想接触下和考虑接触电阻下的枢轨接触表面电流密度云图。在0.1 ms时，图11中由于理想接触下电流急剧升高，电枢表面电流产生集中，并且电流密度最大值在4个棱角处，最大电流密度为7.27 GA/m2.而图12中考虑接触电阻后，在枢轨接触前端并未接触，所以设置电枢前端接触薄层为绝缘材料，从而导致电流密度最大值的位置向后移动。在0.3 ms时，电流密度和洛伦兹力达到峰值，使得枢轨间接触面积增大，所以图11和12中的枢轨表面电流密度分布基本一致，但由于考虑接触电阻下的枢轨表面电阻增大，所以图12中的电流密度的最大值10.1 GA/m2小于图11中的电流密度最大值9.06 GA/m2.1.2 ms为电流下降时刻，枢轨接触表面电流密度集中在电枢前端和中间区域。图12中枢轨接触表面电流密度分布的集中区域相比图11中的集中区域向后移动了，原因在于考虑接触电阻后，由于电流减小，枢轨间接触压力减小，接触面积随之减小，从而导致电枢前端并未和导轨相互接触。

3 结论

通过对理想接触和考虑接触电阻下电磁轨道发射的电磁场分析对比，得到以下结论：枢轨间接触电阻变化规律分为3个阶段，0～0.2 ms为第1阶段，在这阶段中接触电阻急剧增高后迅速减小；0.2～0.5 ms为第2阶段，在这阶段中接触电阻缓慢降低到最低值；0.5～2.0 ms为第3阶段，接触电阻随着电流的减小缓慢增加。接触电阻的改变对电枢喉部的最大电流密度影响较小，同样对电枢发射驱动力的大小影响较小，但垂直于导轨方向的洛伦兹力减小4.0%，对枢轨接触面的最大电流密度影响较大，枢轨接触表面电流密度减小10%，且电流密度集中区域向发射方向的后方移动。