电动轮汽车车速与道路坡度估计*
2020-03-18袁良信郑四发连小珉
陈 浩,袁良信,孙 涛,郑四发,3,连小珉
(1.清华大学汽车工程系,北京 100084; 2.苏州紫荆清远新能源汽车技术有限公司,苏州 215200;3.清华大学苏州汽车研究院,苏州 215200)
前言
随着传统能源与环境问题之间的矛盾日益增加,电动汽车在近十年逐渐成为研究重点与热点[1-2]。电动轮汽车是指采用安装在车轮轮毂内部的电机作为动力源直接驱动行驶的一类电动汽车。电动轮汽车取消了传统的传动机构,简化了车辆底盘的空间布置,从而变得更加节能与安全[3-4]。同时,电动轮汽车能够独立对驱动车轮的转矩进行分配,相比于传统燃油汽车与集中式驱动电动汽车,实现了动力源解耦,因此增加了动力学控制自由度,有助于改善电动汽车的动力性能[5-6]。
车速与道路坡度信息对于动力性相关的电子控制系统都是十分重要的参数[7]。采用四轮驱动行驶的电动轮汽车没有了从动轮转速作为参考,使得车速估计的难度变大。由于惯性传感器的工作原理[8],所采集的纵向加速度信号中叠加了道路坡道信息和干扰噪声,无法直接得到准确的车辆纵向行驶加速度信息,影响相关的动力学控制算法。因此,针对轮毂电机转矩响应迅速和实时转矩与转速信息易获取等特点,有必要对电动轮汽车的车速与道路坡道估计方法进行研究。近年来,余卓平等[9]依据车辆加速度传感器信号和车轮滑移率对纵向车速进行估计,通过各个车轮滑移率的大小确定轮速估计算法中反馈修正的比例,理论上证明了纵向车速估计误差的收敛性;采用带遗忘因子的递推最小二乘算法实现了道路坡度的在线估计,进而使用坡度估计值修正加速度信号,实现了坡度自适应纵向车速估计。该方法依赖于试验测得的轮胎纵向力模型,因此适用范围相对较小。冉旭等[10]融合了车辆静止起步时加速度传感器信号与基于纵向动力学的坡度估计结果,根据车速计算对应的置信因子得到坡度估计的原始值;为了防止坡度值的波动引起状态频繁转换,采用广义迟滞滤波方法对原始值进行钝化处理得到最终坡度估计值。但是,依据单步采样实时数据进行参数估计,忽略了历史数据中的有效模型信息,无法保证参数估计的统计特性。褚文博等[11]针对电动轮汽车纵向驱动转矩信息准确的特点,设计高通滤波器得到驱动力矩与纵向加速度的高频信号,采用递归最小二乘算法得到整车质量,在此基础上采用运动学和动力学方法联合观测得到道路坡度,解决了坡度估计对模型精度要求高、加速度传感器静态误差影响大等问题。该方法需要获取准确的车辆纵向行驶加速度信息,然而实际纵向行驶加速度信号往往与坡度信号耦合。
本文中针对电动轮汽车纵向运动特性,依据非线性动力学方程,考虑历史数据中的模型信息,设计1阶扩张状态观测器对正常行驶工况,即车轮不发生打滑时,电动轮车辆的车速与道路坡度进行联合估计,降低了估计模型对建模精度的依赖;采用带遗忘因子的递归最小二乘方法从原始加速度传感器信号中分离道路坡度信息,融合两类坡度信息,得到最终道路坡度估计值。通过联合仿真模型与实车试验验证方法的可行性与实际效果。
1 纵向动力学模型
电动轮车辆行驶过程中纵向受力[12]如图1所示。
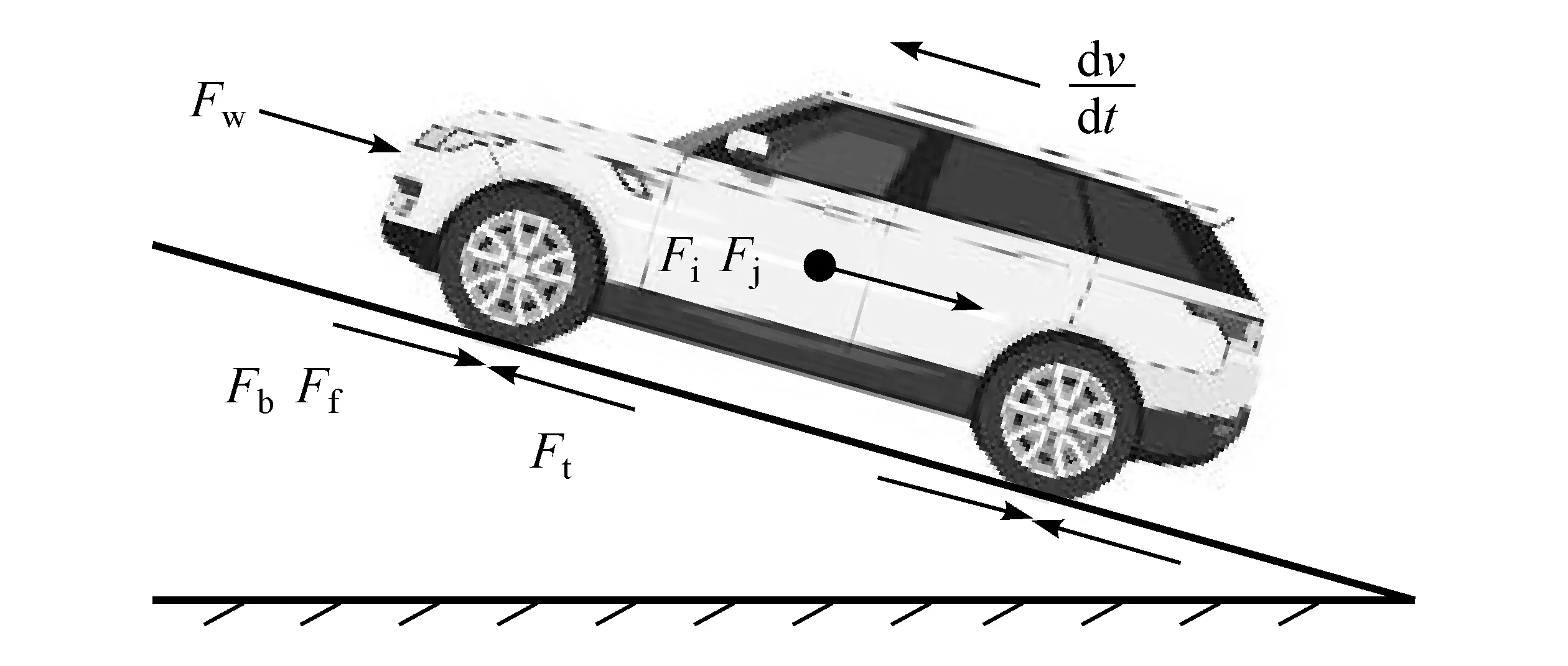
图1 电动轮行驶纵向受力示意图
由图1可知,电动轮车辆在纵向受到驱动力Ft、空气阻力Fw、道路阻力Fψ(坡道阻力Fi与滚动阻力Ff之和)、加速阻力Fj和制动力Fb的共同作用。纵向非线性动力学方程如下:

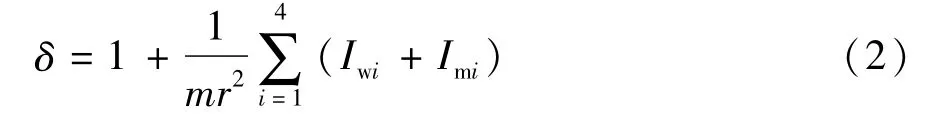
式中:Iwi为车轮转动惯量;Imi为轮毂电机转子部分转动惯量。
2 车速与坡度联合估计
2.1 扩张状态观测器设计
扩张状态观测器将系统非线性部分作为扩张状态,并将线性误差反馈修正项替换为非线性函数,使观测器不依赖于系统非线性环节的具体数学模型,也无须直接测量其作用。由于汽车纵向运动可以表示式(1)所示的非线性过程,因此通过设计合适的观测器参数能够完成运动状态的估计,并保证状态收敛,同时提高状态观测器的效率。
典型1阶非线性系统的状态空间[13]可表示为
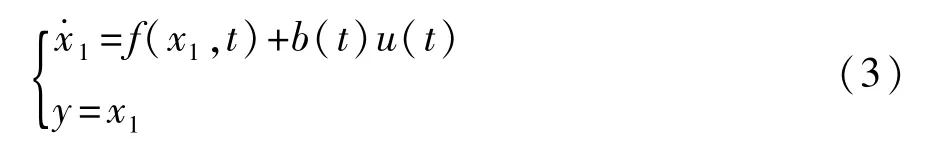
当如式(3)所示的非线性系统满足以下条件:
(1)|f(x1,t)|≤M,即有界,但不要求f(x1,t)的连续性;
(2)b(t)可以确定。
定义系统非线性环节f(x1,t)为扩张状态变量x2,即


式中:z1和z2为观测器的状态变量,分别与原始系统(式(5))中的x1和x2对应;e1为实际测量结果x1与估计状态z1之间的差值,即估计误差,扩张状态观测器也正是基于估计误差动态调整估计结果,使得估计结果收敛;fal(e,a,l)为原点附近具有线性段的连续幂次非线性函数,l(l>0)为非线性段的长度。

式中:h为离散步长,即采样间隔;β1、β2、a1、a2和l为观测器设计参数(β1,β2,a1,a2,l>0)。
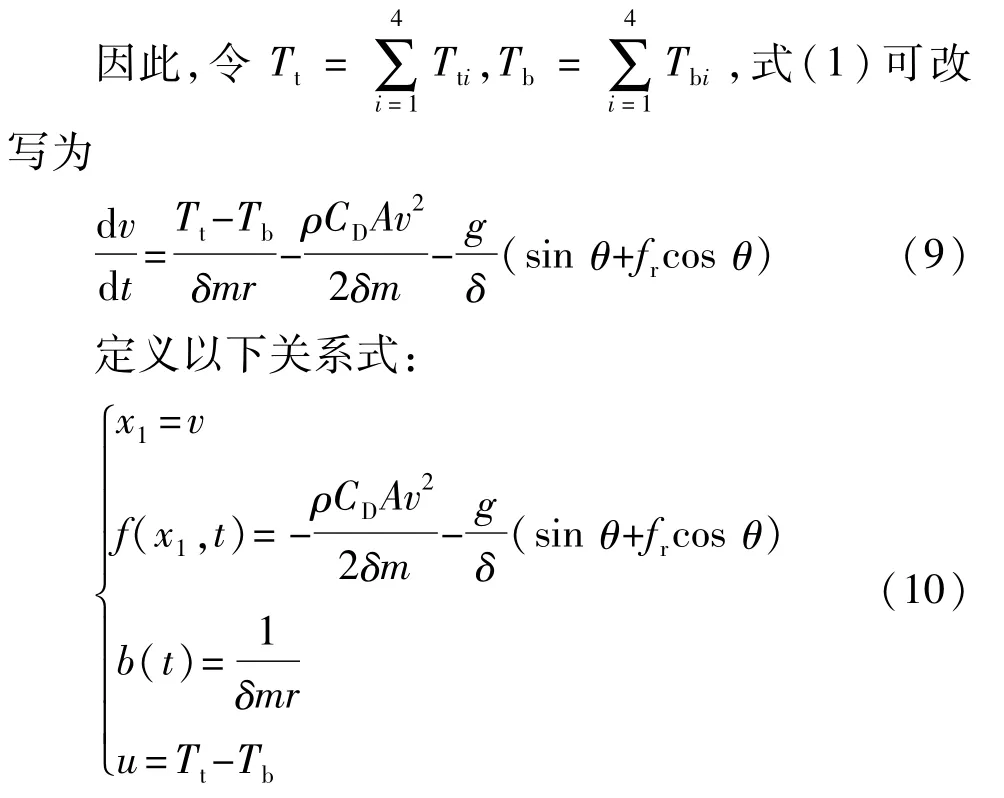
由式(10)可知,车辆实际行驶速度和道路坡度在一定范围内,因此非线性环节f(x1,t)有界,b(t)由整车质量和车轮滚动半径确定,均满足扩张状态观测器的设计条件。
离散扩张状态观测器表示为
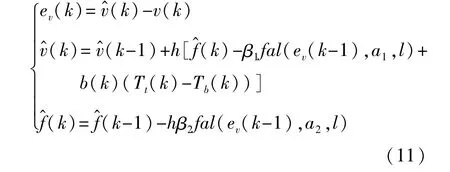

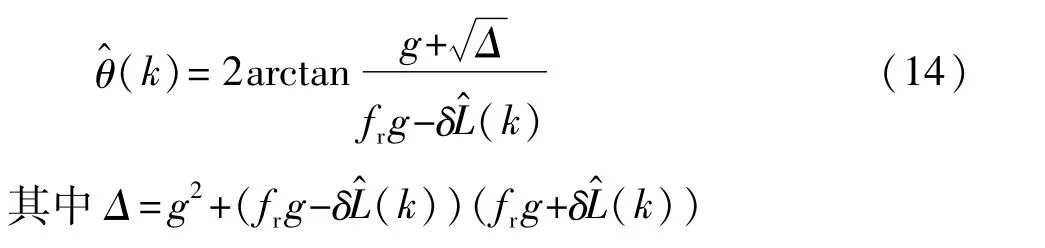
2.2 稳定误差分析
由于|f(x1,t)|≤M,并假设f(x1,t)=W0,代入式(5)和式(6),则车速估计误差为
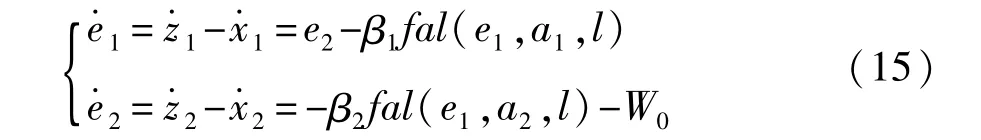
当误差系统进入稳态时,e·
1=0,e·
2=0,则有以下关系成立:

选取设计参数满足β2≫W0,使稳态误差趋于0,即观测状态与系统真实状态等价。
2.3 基于加速度的坡道信息估计
加速度传感器测得的信息中包含车辆纵向加速度信息及道路坡度信息,具体关系为

将式(14)代入式(18)中,采用后向欧拉法进行离散,整理可得
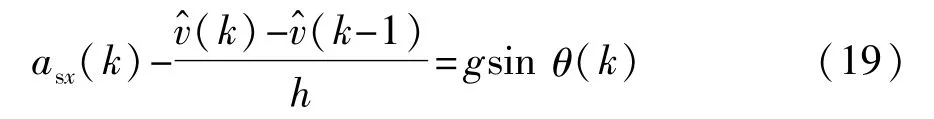
递归最小二乘法(recursive least square,RLS)是系统辨识的一种方法,针对时变系统,每更新一次观测数据能够实现对辨识参数的修正,广泛用于参数在线估计,通过递归迭代减少计算量[14]。
为利用历史数据中的有效信息,克服因为数据增长带来的“数据饱和”问题,采用带遗忘因子的递归最小二乘方法(forgetting factor recursive least square,FFRLS),对道路坡度进行估计,解决坡度时变跟踪问题,迭代过程可表示为
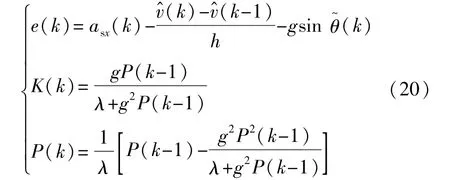
式中λ为遗忘因子,λ∈[0.9 1],数值越小,表示历史数据的衰减率越高。
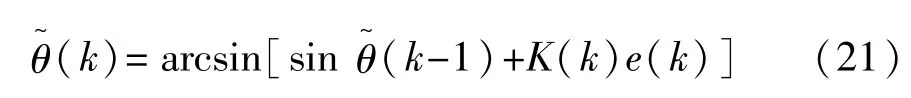
2.4 坡道信息融合
由于扩张观测器是基于动力学方程得到的结果,适用于车辆动态过程中的坡度估计,而纵向加速度传感器在忽略俯仰运动的前提下,车辆静态时的输出结果可直接解算道路坡度值。因此,车辆纵向运动加速度不大时,针对扩张状态观测器估计值与纵向加速度传感器估计值,依据车辆行驶速度设置比例系数完成两类信息的融合:

式中:θe为融合得到最终道路坡度估计值;和分别为和的比例系数,如式(23)和式(24)所示。
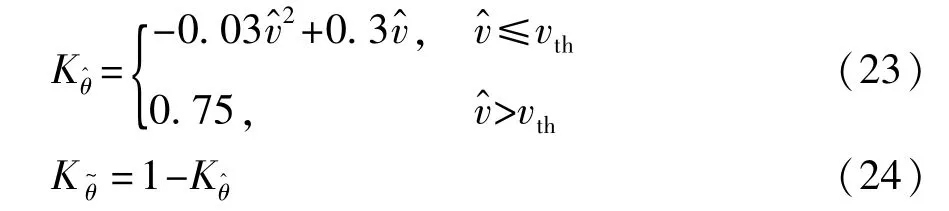
式中vth为速度门限值,可根据实际车辆间的差异进行标定,本文中取5 km/h。
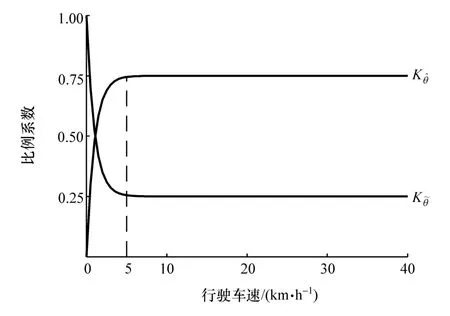
图2 信息融合比例系数
2.5 车速信息估计
根据离散扩张状态观测器的表达式(11),可得车速估计值ve(k):

3 仿真结果
依照前述联合估计方法在MATLAB/Simulink中搭建参数估计模型,通过Carsim模拟电动轮车辆的动力学特性进行联合仿真以验证方法可行性。联合仿真模型逻辑关系如图3所示。
图3中,首先设置Carsim与MATLAB/Simulink的输入与输出数据接口模块;其次,MATLAB/Simulink从Carsim中提取车轮实时驱动转矩信号Tti(i=1,2,3,4)、车轮实时制动转矩信号Tbi(i=1,2,3,4)、车轮实时转速信号ni(i=1,2,3,4)和加速度信号asx,通过扩张状态观测器模块得到估计车速v^与坡度信号并且v^即为车速估计结果ve输出。同时,递归最小二乘模块利用v^与asx得到坡度信号;最终,坡度信息融合模块以v^为依据将与融合得到坡度信号θe,并作为坡度估计结果输出。
车辆模型与参数估计模型的设计参数如表1和表2所示。
图3 联合仿真模型结构图
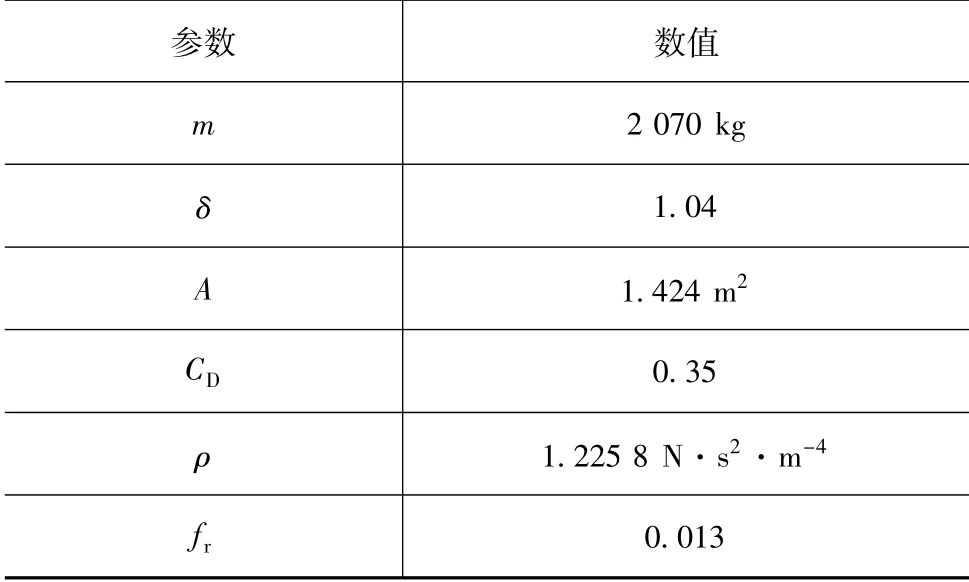
表1 车辆模型参数
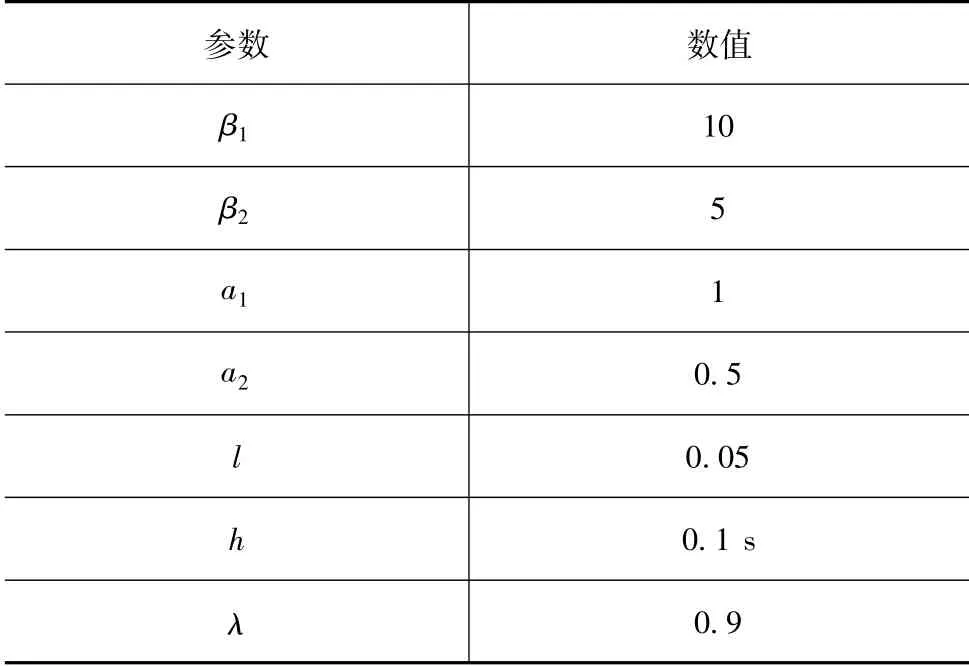
表2 参数估计模型参数
仿真工况设置为0%-3%-0%变坡度路面,由驾驶员模型控制行驶车速[15],使车辆在平路以初始速度0起步,加速至稳定车速20 km/h,仿真结果如图4和图5所示。
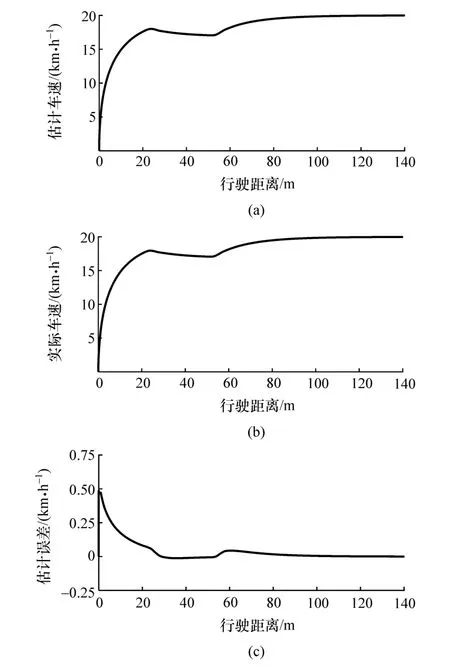
图4 行驶车速仿真结果
如图4所示,行驶距离表示车辆当前行驶位置与起始位置的距离。图4(a)表示由扩张状态观测器得到的估计车速;图4(b)表示车轮转速换算得到的实际车速。车辆在前20 m内,行驶在平直路面,车速逐渐增加至17 km/h;20~60 m内,车辆行驶经过坡道路面,由于坡道阻力作用,车速下降;60 m后,车辆再次进入平直路面,车速稳定至20 km/h。图4(c)表示估计误差,初始估计误差处于0.5 km/h左右,随着车辆速度增加,估计车速逐步收敛至0,即估计车速信息与实际车速信息等价。
4 实车试验
采用国产某款运动多功能车型(SUV)搭载轮毂电机作为电动轮汽车试验平台[16],并在自主研发的矢量控制器(torque vectoring controller,TVC)内集成估计算法,硬件拓扑结构如图6所示。
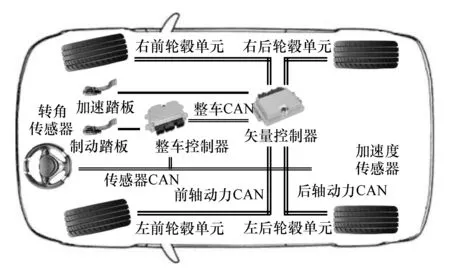
图6 试验平台硬件拓扑结构图
图中:前后轴轮毂电机分别通过前轴动力CAN、后轴动力CAN与矢量控制器进行通信,传递车轮实时转矩与转速信息;加速度传感器通过传感器CAN与整车控制器进行通信;同时,整车控制器采集制动踏板开度信息,通过整车CAN将加速度信息与制动踏板开度信息传递至矢量控制器。试验车辆采用VBOX直接采集实际车速,通过内置GPS(刷新频率为100 Hz)得到车辆实时行驶速度信息,精度为0.1 km/h。
选取产业园区内实际坡道路面进行测试,如图7所示。
实车测试过程中,车辆从平路静止起步,驾驶员操纵加速踏板和制动踏板行驶至坡道路面,并控制车辆速度平稳过渡至25 km/h,以此测试电动轮汽车车速与道路坡度信息估计的准确性和实时性。

图7 实车道路测试图
4.1 加速度信号预处理
加速度传感器采集的耦合道路坡度信息的信号受环境因素干扰,容易携带高频噪声。因此,设计1阶惯性环节模拟低通滤波器对加速度信号进行预处理[10],如式(26)所示。

式中:τ为时间常数,取为0.5 s;s为拉普拉斯算子。离散形式为
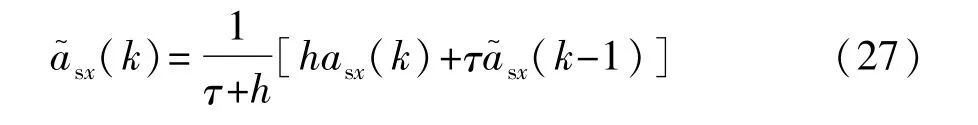
实车测试得到的加速度滤波对比信号如图8所示。
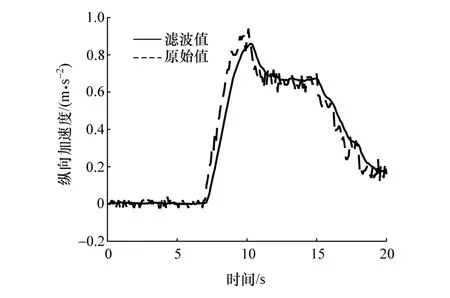
图8 加速度信号滤波对比图
由图8可知,滤波后的加速度信号去除了原始信号中的高频噪声,能够表征实际车辆加速度的变化。然而滤波方法会带来信号延迟,但延迟时间小于控制器数据更新周期(50 ms),满足输入信号的实时性要求。
4.2 实车试验结果
实车测试结果如图9和图10所示。
由图9可知,估计车速与实际车速同步增加,估计误差最大值为0.25 km/h,并随着车速的增加逐步收敛。整个测试路段内,车速估计误差小于1%。
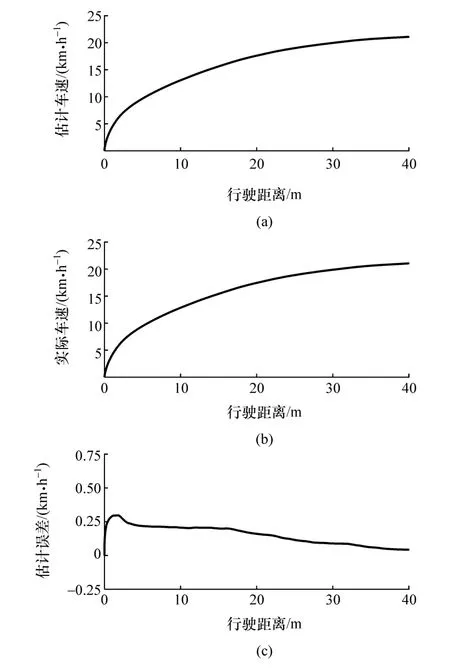
图9 行驶车速实车测试结果
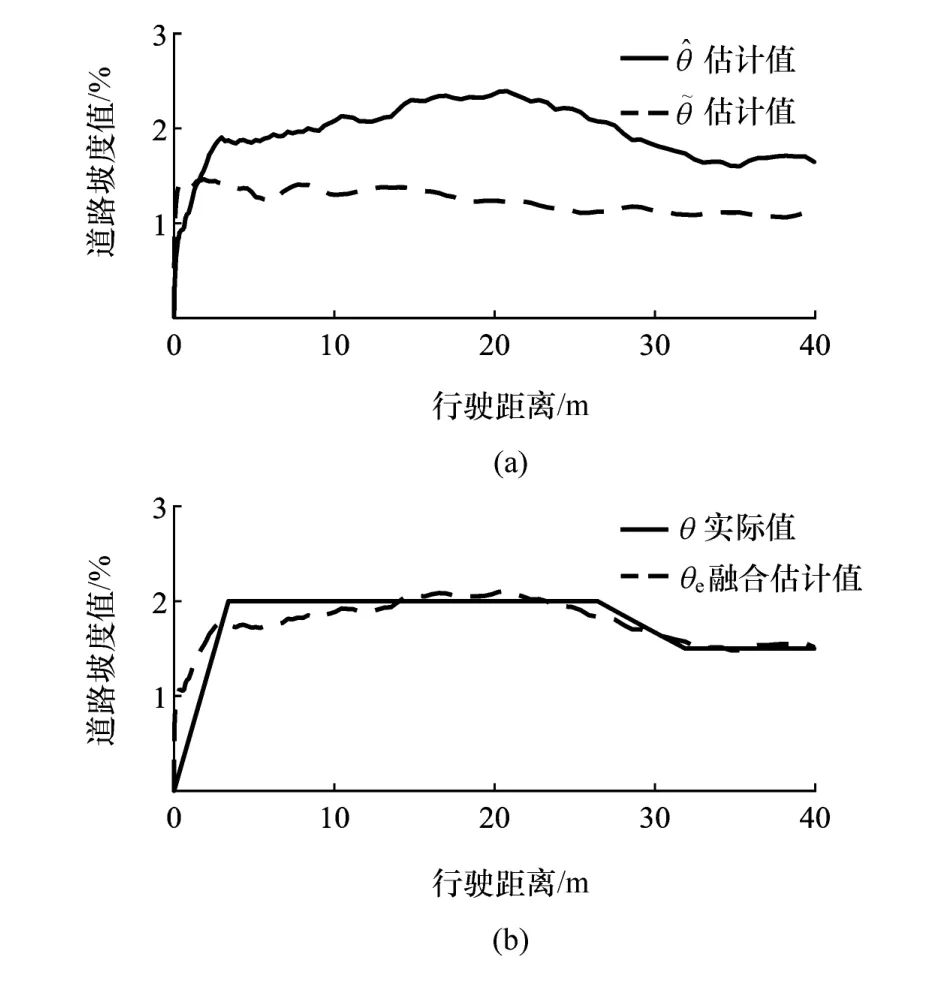
图10 道路坡度实车测试结果
5 结论
本文中针对电动汽车车速与道路坡度估计问题,结合车轮转矩与转速信息易提取的特点,提出了基于扩张状态观测器的车速估计方法和扩张状态观测器与加速度传感器信息融合的道路坡度估计方法,并在此基础上完成了仿真与实车验证,得到以下几点结论:
(1)设计1阶扩张状态观测器对电动轮汽车的车速与道路坡度进行联合估计,将车辆未知非线性环节扩张为新的状态变量进行估计,降低了参数观测对模型精度的要求,提高了方法的可行性;
(2)考虑到历史数据所包含的有效信息和“数据饱和”等问题,采用带遗忘因子的递归最小二乘方法实现了纵向加速度信号中坡度信息的解耦,并设置比例系数对坡度信息进行融合,充分利用了不同数据来源的数据价值;
(3)仿真与实车试验结果能够同步跟踪车速与道路坡度的变化,保证估计误差收敛,所提出的估计方法可行有效,实时性好。
