空中和水下近场爆炸冲击波对靶板作用效应对比分析

郭克强，孙 华，赵 沁，恽炅明，汤 磊

(安徽神剑科技股份有限公司，安徽 合肥 230022)

0 引 言

空气和水是两类最为常见的起爆介质，但由于两种介质的物理属性存在较大差异，导致炸药水下爆炸与空中爆炸特性有许多不同之处，不仅爆炸的物理现象和机理不同，对结构的损伤机制、 破坏程度及防护设计也均有所不同[1]. 爆炸是一种多学科交叉耦合的物理现象，现有理论研究往往需要做相当程度的简化，为真实有效地反映现象，目前研究手段仍以试验和数值模拟研究为主. 聂源等[2]采用SPEED软件对球形装药空中爆炸过程进行了模拟分析，指出了温度、 相对湿度对爆炸冲击波参数的影响规律. 段晓瑜等[3]以试验方法对比分析了TNT等3种炸药不同距离处的冲击波反射超压，并对3种炸药的冲击波超压与对比距离之间的关系进行拟合，获得了炸药空中爆炸的地面反射超压经验公式. 王振雄等[4]进行了两种水底介质、 不同水深情况下的爆炸试验. 通过分析观测点冲击波峰值压力指出，水底介质、 观测点和装药之间的距离对峰值压力影响较大. 王博雅等[5]进行了GUHL-1炸药的水下爆炸试验，分析得出了GUHL-1 炸药水中爆炸冲击波压力峰值和爆距的关系，为反蛙人武器系统的设计提供了参考. 郑成等[6]以四边约束矩形板为研究对象，对其在爆炸冲击波载荷下所产生的塑性大变形响应进行了理论分析和试验研究，并根据板的挠度变形理论和能量守恒原理，建立了矩形板在爆炸载荷作用下发生塑性大变形的弹塑性分析方法. 王金等[7]以数值模拟的方法分析探讨了点蚀损伤钢板结构在空中爆炸冲击波载荷作用下的动态响应特点. 目前，关于近场爆炸冲击载荷、 爆炸结构破坏效应及动态响应的研究多集中于水或空气中的某一介质，且以战斗部静爆为前提. 实际中，战斗部对目标的爆炸冲击波毁伤往往伴随着高速运动，相比于战斗部的静态爆炸冲击波毁伤区别较大. 此外，随着科学技术和高新材料的运用，装药受运载体牵引作用而产生的运动速度得到大幅提高，使得对目标的爆炸毁伤差异更为明显. 由于试验条件的限制及炸药作用的特殊性，关于运动装药在不同介质中爆炸结构破坏效应的研究较少. 聂源等[8]对球形装药空中动态爆炸冲击波超压进行了模拟研究，获得了装药牵引速度及方位角对冲击波超压值的影响规律，但研究结论仅限于球形装药，且未进行装药在水、 空气两种介质中的爆炸结构破坏效应差异分析.

本文主要以数值模拟的方法对比分析了爆炸冲击载荷在水下、 空中的结构破坏效应. 同时研究了装药牵引速度、 形状对靶板作用效应的影响规律. 研究结论可为战斗部及装甲防护的设计提供参考.

1 数值模拟方法有效性验证

数值模拟结果的准确性容易受模型网格尺寸、 材料参数等因素的影响[9]. 为校验模型网格尺寸及材料参数的合理性，参照文献[10]中试验构型建立数值模型并计算. 文献[10]中试验装药采用质量为1 kg、 长径比为1的TNT柱形装药，靶板为400 mm×400 mm×2 mm的正方形Q235钢板，通过螺钉约束在靶架上. 药柱采用单端起爆方式，炸高为1 m，药柱轴向正对靶板中心，物理模型如图 1(a) 所示.

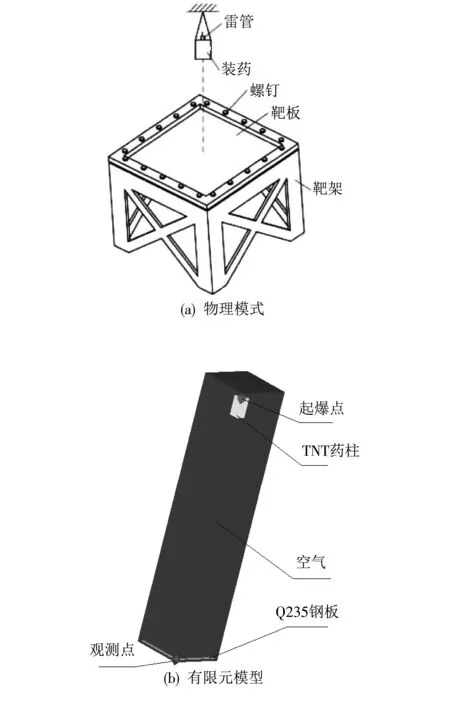
图 1 文献[10]试验构型及对应有限元模型Fig.1 Model corresponding to the experimental configuration of Ref. [10]

利用AUTODYN-3D对问题进行建模和求解. 考虑到物理模型的对称性，建立的1/4有限元模型如图 1(b) 所示. 空气域采用Euler算法，除对称面外，各边界设置空气流出边界条件(Flow_out边界条件)来模拟无限空气域. 靶板采用Lagrange算法, 通过设置固定边界条件，对四边进行全自由度约束. 空气域、 靶板分别采用均匀网格，为提高计算效率和精度，网格尺寸分别设定为4 mm和2 mm. TNT炸药采用标准JWL状态方程[10-12]

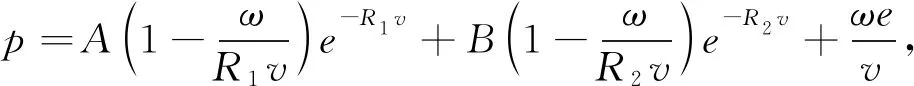
(1)

式中：v为爆轰产物相对比容；e为单位质量内能；A，B，R1，R2和ω为常数.

空气采用理想气体状态方程[10-11]

p1=(γ-1)ρe+pshift,

(2)

式中：p1为压力；γ为多方指数；pshift为压力偏移量；e为比热力学能. 对于空气模型，γ取1.4，ρ取 1.225 mg/cm3，e在mm/mg/ms单位制下取 2.068×105.

水的状态方程采用多项式状态方程[11-13]

p=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0ew.

(3)

当水受拉或空化时(μ<0),其状态方程

p=T1μ+T2μ2+B0ρ0ew,

(4)

式中：A1，A2，A3，B0，B1，T1和T2为常数；μ=ρ/ρ0-1，ρ为水的密度，ρ0为水的初始密度；ew为水的比内能，ew=(ρgh+P0)/ρB0，h为水深，P0为大气压力.

TNT炸药和水的状态方程参数分别见表 1，表 2.

表 1 TNT炸药状态方程参数[10-12]Tab.1 Equation of state parameter of TNT explosive[10-12]

表 2 水状态方程参数[12-14]Tab.2 Equation of state parameter of water[12-14]

靶板为Q235钢板，状态方程选用Shock[10-11]，模型为Mie-Gruneisen方程

p=pH+φρ(e-eH),

(5)

其中φρ为Gruneisen常数，压力pH和能量eH的计算公式分别为

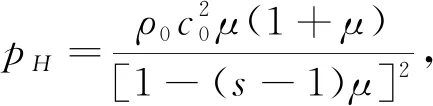
(6)

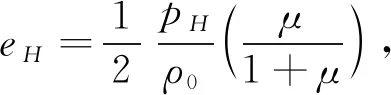
(7)

式中：μ=ρ/ρ0-1，ρ0为材料初始密度，ρ为材料密度；c0为材料声速. 质点速度方程为

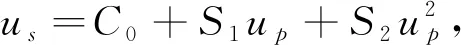
(8)

式中：up为冲击波速度；C0,S1和S2为试验常数. 靶板强度模型选用Blinear Hardening模型，模型的应力方程为

σ=σ0+EPε,

(9)

表 3 Q235材料状态方程及材料模型参数[10-11]Tab.3 Equation of state and material parameters of Q235 steel[10-11]

表 4 模拟结果与试验数据[10]对比Tab.4 Comparison between simulated results and experimental data[10]

分析表 4 数据可知，数值模拟结果与试验值较为符合，误差约为6.9%(主要原因是相比于数值模拟中靶板周边的理想约束，试验中以螺钉压紧方式的靶板受拉力作用后变形较大)，验证了模型网格尺寸及材料参数的合理性.

采用与验证模型相同的网格尺寸及材料参数建立新的计算模型，对比分析不同形状装药爆炸冲击载荷在不同起爆介质中(水下、 空中)对圆形靶板结构的破坏效应.

2 数值模拟结果分析

2.1 不同介质中爆炸冲击波对靶板作用效应对比分析

为研究不同形状装药在空中、 水下两种起爆介质中爆炸冲击波对靶板的毁伤效应，建立了炸高400 mm，质量500 g的3种形状装药(长径比为1、 2的柱形装药及球形装药)对厚度 5 mm 靶板的爆炸冲击模型，其中靶板为半径150 mm 的Q235钢板. 同时，在靶板中心及距靶板中心 150 mm 处分别设立观测点，物理模型见图2(a). 考虑到对称性及计算效率，建立1/4有限元模型，如图2(b)所示.

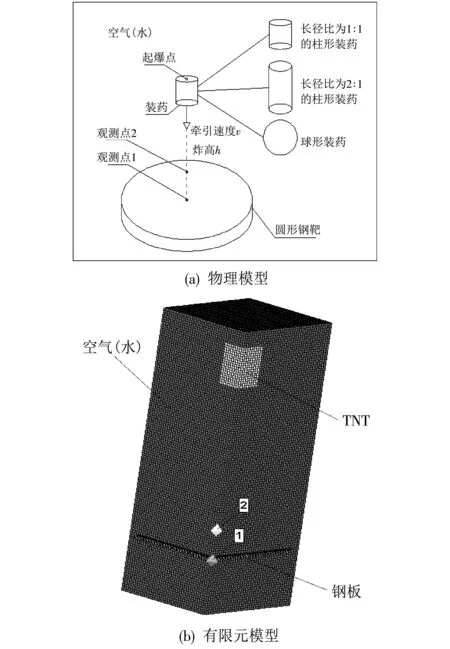
图 2 装药爆炸模型Fig.2 Explosion model of charge

提取观测点2在不同工况下对应的压力时程曲线，如图 3 和图 4 所示.

通过观察图 3 发现，当装药水下爆炸所产生的冲击波传播到观测点2处时，3种形状装药对应冲击波压力均迅速到达峰值，其中长径比为1的柱形装药对应压力峰值最大(约为162.3 MPa)，球形装药对应压力峰值次之(约为158.25 MPa)，长径比为2的柱形装药对应压力峰值最小(约为137.5 MPa). 由图 4 可知，当空中爆炸冲击波传播到观测点2处时，所提取的冲击波压力时程曲线与水下爆炸冲击波传播规律相似，但压力峰值均远小于水中对应观察点压力峰值.

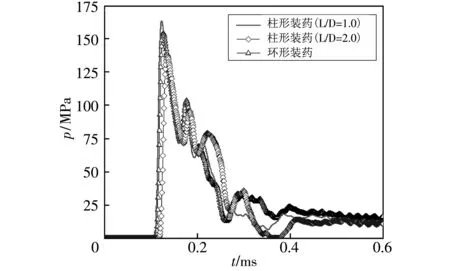
图 3 不同工况下装药水下爆炸对应压力时程曲线Fig.3 Pressure time history curve of charge underwater explosion under different working conditions

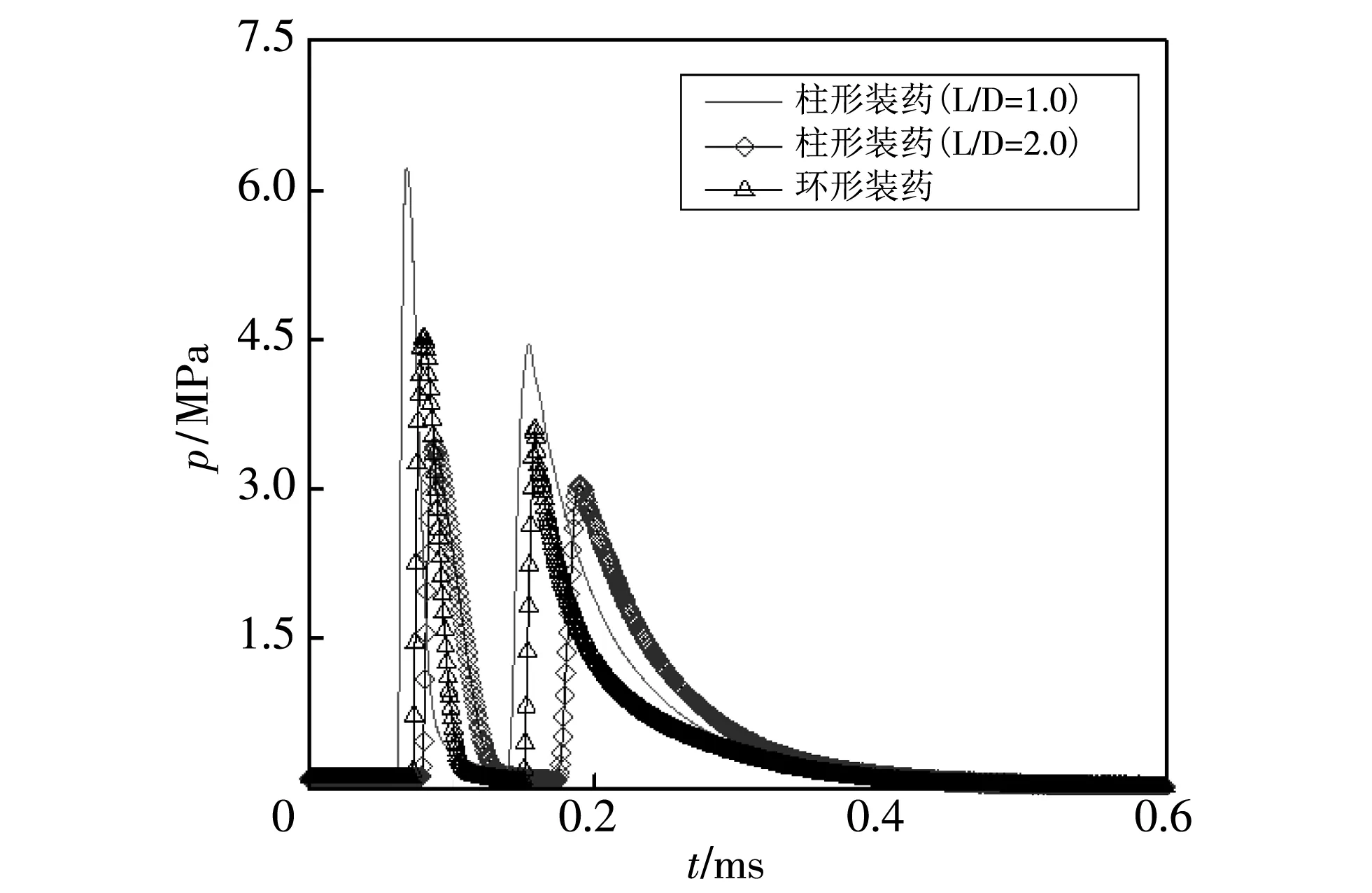
图 4 不同工况下装药空中爆炸对应压力时程曲线Fig.4 Pressure time history curve of charge air explosion under different working conditions

对比分析图 3 和图 4 可知，由于空气密度相比水较小，可压缩性大，使得近爆区域冲击波在空中传播速度比在水下快，空中观察点2到达压力峰值所用的时间比水中短.

为进一步分析不同形状装药在空中、 水下两种介质中所产生的爆炸冲击波对靶板的毁伤效应，提取不同工况下对应靶板中心点挠度曲线，如图 5 和图 6 所示.

图 5 不同工况下装药水下爆炸对应靶板中心点挠度曲线图Fig.5 Deflection curves of the center point of target for underwater explosion under different working conditions

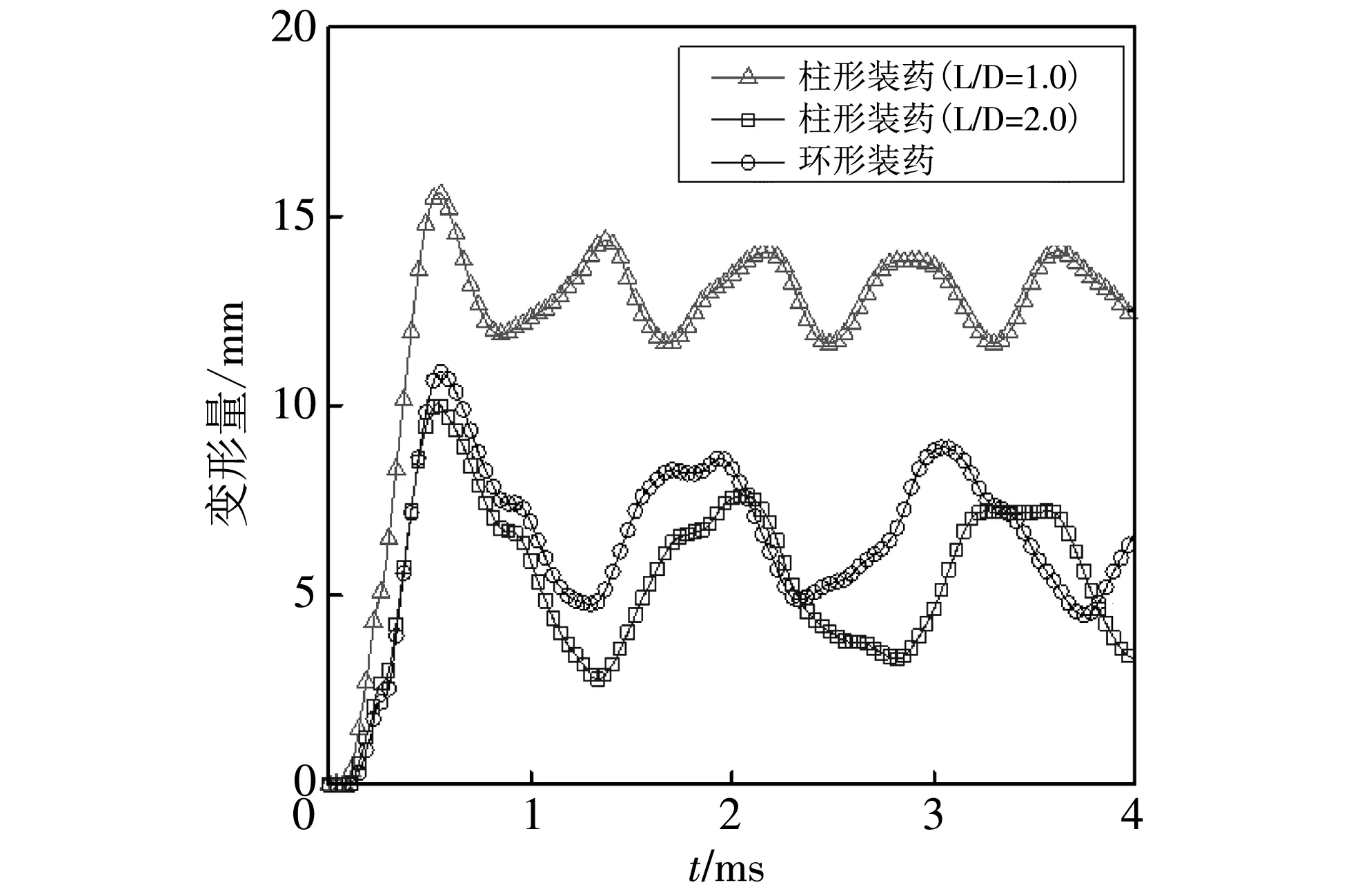
图 6 不同工况下装药空中爆炸对应靶板中心点挠度曲线图Fig.6 Deflection curve of the center point of the target for charge air explosion under different operating conditions

通过观察图 5 和图 6 可知，无论是在空中还是水下，长径比为1的柱形装药对应靶板中心点挠度值最大，球形装药次之，长径比为2的柱形装药对应靶板中心点挠度值最小. 产生该现象的原因除起爆方式的差异，还受装药结构的影响. 由于柱形装药的冲击波场不同于球形装药的规则对称，冲击波传播过程会出现局部高超压区现象；随着柱形装药长径比的增大，装药轴线方向的高超压区呈现减小趋势. 而且，长径比为1的柱形装药、 球形装药所对应靶中心点的挠度值在空中所表现出的差异相对水中条件较明显.

此外，通过计算分析可知，水中长径比为1的柱形装药(球形装药)对应靶板中心点的挠度值是空中的1.67倍(2.95倍)，这是由于冲击波在空气中传播时大部分能量快速地耗散在空气中，该现象与前节冲击波场分析结果相一致.

2.2 不同牵引速度工况下爆炸冲击波对靶板作用效应影响分析

为研究装药在不同牵引速度工况下爆炸冲击波对靶板的毁伤效应，建立了炸高400 mm，质量500 g 的3种形状装药(长径比为1、 2的柱形装药及球形装药)对厚度5 mm靶板的爆炸冲击模型. 计算分析了3种形状装药在不同牵引速度(v=0, 100, 200, 300, 400, 500 m/s)条件下对应靶板中心点挠度值，得到了典型时刻靶板变形云图，如图 7 和图 8 所示.

图 7 柱形装药(L/D=1)空中爆炸对应靶板变形云图Fig.7 Deformation nephogram of target plate corresponding to air explosion of cylindrical charge (L/D=1)

图 8 柱形装药(L/D=1)水中爆炸对应靶板变形云图Fig.8 Deformation nephogram of target plate corresponding to underwater explosion of cylindrical charge (L/D=1)

通过观察图 7，图 8 可知，无论是在空中还是水下，柱形装药(长径比为1)爆炸冲击波使靶板受力变形，其中靶板中间部分是应力集中区域，也是变形量最大位置. 此外，在装药牵引速度的影响下，对应靶板的变形量明显增大.

为深入了解装药在不同牵引速度下对靶板的毁伤效应，提取并绘制了靶板中心点的挠度峰值随装药牵引速度变化曲线，如图 9 和图 10 所示.

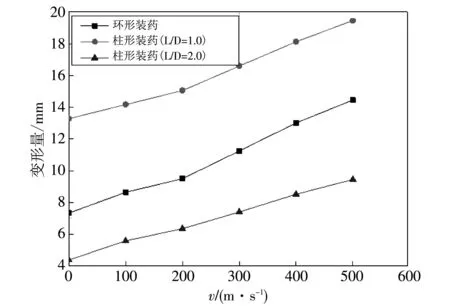
图 9 不同工况下装药空中爆炸对应靶板中心点挠度峰值曲线Fig.9 The peak deflection curve of the center point of the target for charge air explosion under different working conditions

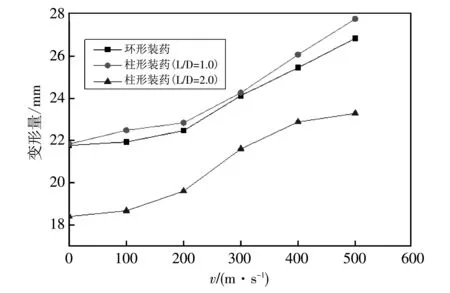
图 10 不同工况下装药水下爆炸对应靶板中心点挠度峰值曲线Fig.10 Peak deflection curve of target center point corresponding to underwater explosion under different working conditions

通过分析图 9 和图 10 可知，无论空中还是水下，随着装药牵引速度的增加，3种装药对应靶板中心点的挠度峰值呈现增长趋势，但长径比为1的柱形装药所对应靶板中心点挠度值始终最大. 此外，即使在牵引速度的影响下，长径比为1的柱形装药、 球形装药对应靶板中心点挠度值在空中所表现出的差异相对于水中也更为明显.

当装药牵引速度v=500 m/s时，球形装药、 长径比为1的药柱及长径比为2药柱空中(水下)对应冲击靶板的中心点挠度峰值相对于静态(v=0 m/s)分别提高了97.2%(23.3%), 46.5%(28.9%)和115.8%(25.4%).

3 结 论

1) 数值模拟再现了空中、 水下近场爆炸冲击波对靶板的作用效应规律，模拟结果与文献试验结果较吻合，验证了数值模拟方法的有效性.

2) 不同形状装药在空中、 水下两种起爆介质中所产生的爆炸冲击波对靶板的毁伤效应差异较大； 由于空气与水两种起爆介质物理属性的差异，3种形状装药水中爆炸所产生的冲击波压力峰值均远大于空中对应观察点压力峰值； 同一介质中，不同形状装药对应靶板中心点的挠度值也有所差异，长径比为1的柱形装药对应靶板中心点挠度值最大，长径比为2的柱形装药对应靶板中心点挠度值最小.

3) 装药在不同牵引速度工况下，对靶板的毁伤效应有所差异： 随着装药牵引速度的增加，靶板中心点的挠度峰值逐渐增大； 当装药牵引速度v=500 m/s时，球形装药、 长径比为1的药柱及长径比为2药柱空中(水下)对应冲击靶板的中心点挠度峰值相对于静态(v=0 m/s)分别提高了97.2%(23.3%), 46.5% (28.9%)和 115.8%(25.4%).