极端工况下某汽车前横向稳定杆的轻量化分析

王步云，曹睿鑫，侯 健，许俊峰，张艳岗，魏福祥

(中北大学 能源动力工程学院，山西 太原 030051)

随着日益严格的排放法规和石油资源的逐渐匮乏，降低油耗、 减少排放成为各大汽车厂商的关注重点. 有研究表明，汽车每减重1 kg，每百公里汽车节油0.01 L[1]. 因此，在不影响汽车前后悬架侧倾刚度的情况下，汽车的轻量化显得越来越重要[2].

目前，国内外众多机构在车用横向稳定杆轻量化方面已经开展了大量研究工作. 上海交通大学对横向稳定杆采取空心化设计, 同时将稳定杆更换为高强度钢来减轻质量以提高行驶稳定性[3]，德国Mubea和 ThyssenKrupp两个公司在设计高应力横向稳定杆方面处于领先地位，目前已经具有开发高应力空心横向稳定杆的生产制造核心技术. Mubea公司研发的空心横向稳定杆的质量减轻率可达到40%以上. ThyssenKrupp公司与波兰的Silesian University of Technology联合研究了空心横向稳定杆的设计运算方法. 运用于现代汽车领域的技术和结构解决方案同样可以用于研究空心横向稳定杆的结构、 设计和制作过程[4-6].

本文以高尔夫6的横向稳定杆轻量化为研究目标，对其结构进行了优化. 常见的轻量化方式有两种，一是换成质量更轻的材料[7]，二是对横向稳定杆进行空心化. 两种方法各有优缺点，方法一虽然减重效果很好，但成本太高； 方法二的成本相对低，但无法保证其强度刚度条件. 本文解决了第二种方法的缺点，将横向稳定杆进行了空心化处理，同时为了满足实际工况的需要，采用高强度钢材料，并对轻量化后的横向稳定杆进行了两种极端工况分析以及扭转刚度分析和模态分析，最后通过强度刚度实验证明了轻量化后的横向稳定杆满足实际要求.

1 轻量化方案

高尔夫6汽车原横向稳定杆采用的是弹簧钢材质[8]，其质量为7.877 kg. 对横向稳定杆采用空心化和高强度钢处理后的质量为 6.316 kg，相比于原横向稳定杆减重1.561 kg，减重质量是原质量的20%. 高尔夫6汽车原横向稳定杆的直径为28 mm，空心化后壁厚8 mm. 原横向稳定杆的三维图如图 1 所示，轻量化后的横向稳定杆如图 2 所示.

图 1 原横向稳定杆的三维图Fig.1 Three-dimensional map of original horizontal stabilizer bar

图 2 轻量化后的横向稳定杆的三维图Fig.2 Three-dimensional map of lightweight horizontal stabilizer bar

2 强度刚度分析

2.1 前处理

将Solidworks三维软件绘制的原横向稳定杆模型和轻量化后的模型保存为ANSYS能识别的iges格式. 对原横向稳定杆和轻量化后的稳定杆定义材料属性如表 1 所示. 因为横向稳定杆是不规则图形，因此采用自由网格划分，划分精度为6. 原横向稳定杆节点数为41 286，单元数为25 468； 轻量化后的节点数为89 502，单元数为 52 595. 网格划分如图 3 所示.

表 1 材料属性Tab.1 Material Properties

图 3 网格划分图Fig.3 Grid partition diagram

2.2 约束加载

根据前横向稳定杆在高尔夫6中安装的位置，可以得出约束的施加方向. 横向稳定杆左右两端通过螺栓安装在悬架上，中间部分通过套筒与车架连接，而且横向稳定杆可以在套筒内转动，因此约束横向稳定杆的两个套筒处位置.

2.3 极端工况应力及位移分析

2.3.1 一侧车轮垂向跳动工况

以大众高尔夫6汽车为研究对象，整车质量1 315 kg，通过在ADAMS/Car虚拟样机中仿真一端车轮垂向跳动的工况，得出作用在横向稳定杆一端Z方向的力为500 N. 在ANSYS有限元软件中划分网格，约束模型，稳定杆的中间部分约束UY,UX,UZ,ROTY,ROTZ, 因为稳定杆可以转动，因此不约束ROTX方向的旋转自由度[9]. 由图 4，图 5 可知，原横向稳定杆的最大位移为 0.003 086 m，最大应力为160 MPa； 优化后的横向稳定杆最大位移为 0.003 19 m，最大应力为233 MPa.

图 4 原横向稳定杆应力分布图Fig.4 Stress distribution of original horizontal stabilizer bar

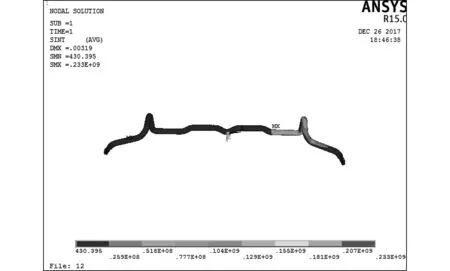
图 5 优化后横向稳定杆应力分布图Fig.5 Stress distribution of optimized lateral stabilizer bar

通过分析可知，原横向稳定杆和轻量化后的横向稳定杆的最大应力都出现在套筒处，应力分布位置未发生改变. 比较图 4 和图 5 可知，最大应力增大了73 MPa，这是由优化后的稳定杆采取空心化的处理所致，但仍然在高强度钢的许用应力范围之内.

如图 6，图 7 所示，原横向稳定杆和化后的稳定杆的最大位移都出现在最右端，即施加压力的地方，最大位移的分布位置未发生改变，位移由原来的 0.003 086 m 增加到了 0.003 19 m ，增加了 0.1 mm.

图 6 原横向稳定杆位移图Fig.6 Displacement diagram of original horizontal stabilizer bar

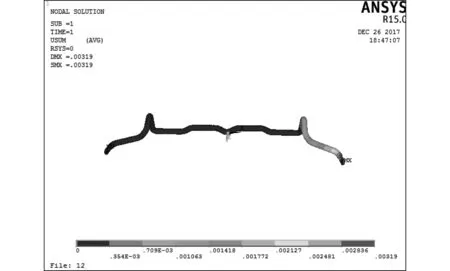
图 7 优化后横向稳定杆的位移图Fig.7 Displacement diagram of optimized lateral stabilizer bar

2.3.2 两侧车轮向相反方向垂向跳动工况

根据ADAMS/Car虚拟样机中模拟出的两侧车轮向相反方向跳动的工况[10]得出载荷，在横向稳定杆的两侧施加500 N，且方向相反. 约束套筒的UY,UX,UZ,ROTY,ROTZ方向，如图 8，图 9 所示，原横向稳定杆最大应力为158 MPa，最大位移为 0.003 083 m； 优化后的稳定杆的最大应力为 232 MPa，最大位移为 0.003 1 m.

原横向稳定杆和改进后的横向稳定杆的最大应力都出现在套筒附近，因为套筒约束了5个自由度，最大应力的分布没有改变，只是应力增大了 74 MPa，这是因为对原横向稳定杆进行了空心化的处理，但是仍然在高强度钢的许用应力范围之内.

图 8 原横向稳定杆应力图Fig.8 Stress diagram of original horizontal stabilizer bar

图 9 优化后的稳定杆应力分布图Fig.9 Stress distribution diagram of optimized stabilizer bar

如图 10，图 11 所示，原横向稳定杆和优化后的稳定杆的最大位移都出现在横向稳定杆的两端，最大位移发生位置未改变，最大位移由原来的 0.003 083 m 增加到了 0.003 317 m，增加了 0.2 mm，这是因为对原横向稳定杆的进行了结构上的空心化.

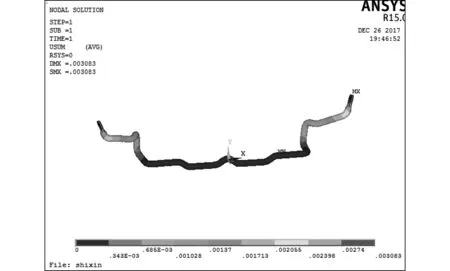
图 10 原横向稳定杆的位移图Fig.10 Displacement map of the original horizontal stabilizer bar

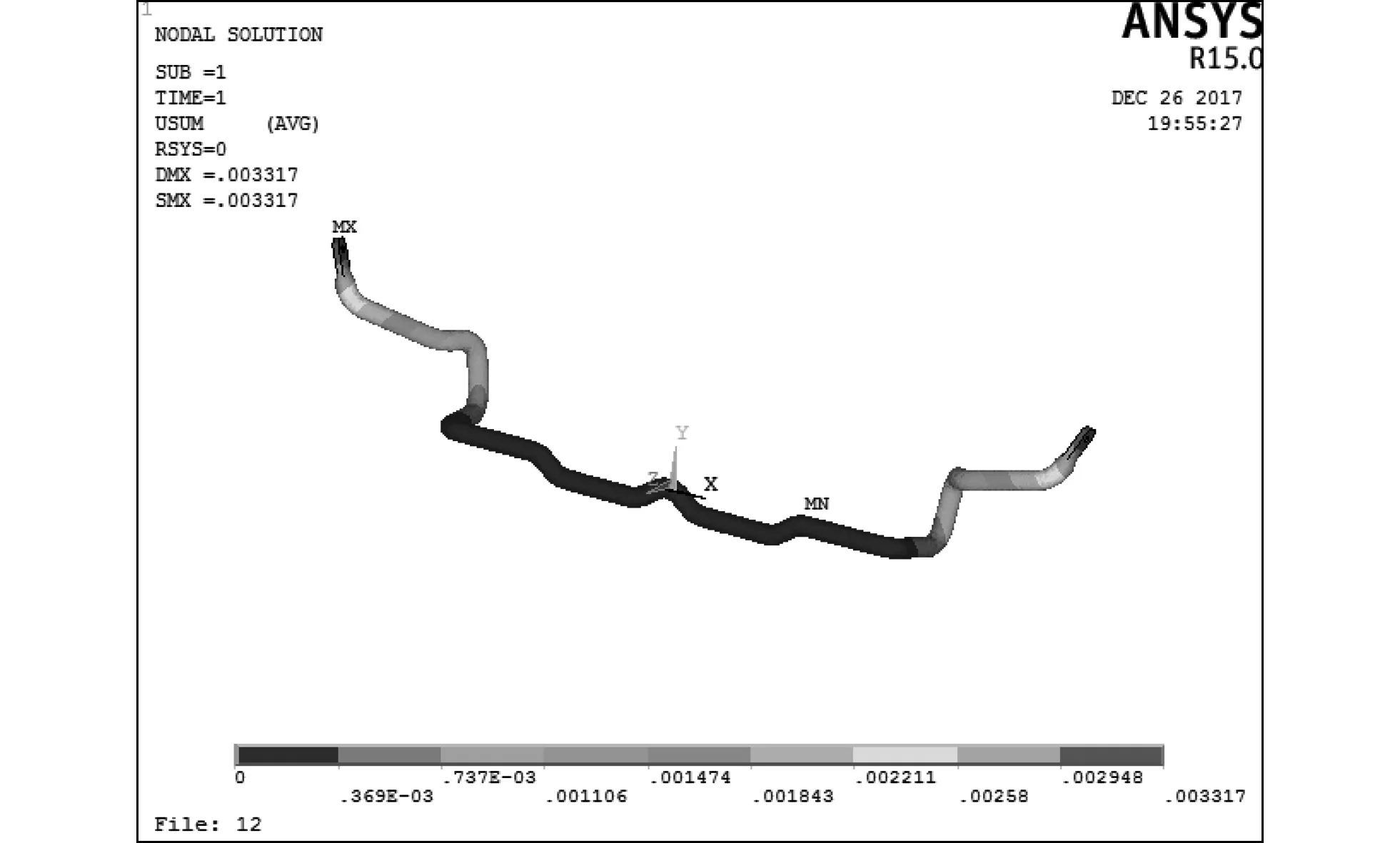
图 11 优化后稳定杆的位移图Fig.11 Displacement map of optimized stabilizer bar

3 模态分析

3.1 理论模态

理论模态分析是将线性定常系统振动微分方程组中的物理坐标变换为模态坐标，然后使方程解耦，并表述成以模态坐标和模态参数表示的独立方程，求解其模态频率[11].

系统微分方程为

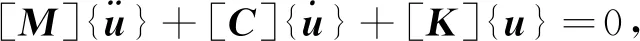
(1)

式中： [M]，[C]，[K]分别为质量矩阵、 阻尼矩阵和刚度矩阵； {u}为位移向量. 对于自由模态而言，横向稳定杆的振动是无阻尼振动，所以[C]为0，得

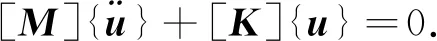
(2)

系统特征方程为

[K-wi2M]{Φ}=0.

(3)

特征方程的解就是所要求的模态频率[12]. 参照高尔夫6车型，横向稳定杆s=1 125 mm，横向稳定杆的直径d=28 mm，空心化后壁厚为8 mm，高强度钢密度为7 900 kg/m3. 计算前6阶的固有频率接近于0，因此从第7阶开始分析，结果如表 2 所示.

3.2 自由模态

利用有限元软件ANSYS对原横向稳定杆与优化后的稳定杆进行自由模态分析. 高尔夫前横向稳定杆的建模是柔性建模，因此前10阶均为弹性变形. 同时前6阶模态接近于0，因此从第7阶模态开始考虑. 对比理论模态、 有限元模态和原横向稳定杆模态结果如表 3 所示.

从表 3 可以看出，以优化后的横向稳定杆为研究对象，对比理论计算模态和有限元分析模态，数值基本相同，误差在3%以内，证明有限元分析的准确性. 然后通过有限元方法，对比优化后的横向稳定杆与原横向稳定杆，可以看出固有频率相差不大，因此优化后的横向稳定杆和原横向稳定杆一样，不会发生共振现象.

3.3 约束模态

通过理论计算证明了有限元分析的准确性，因此利用有限元法进行进一步的分析. 由于高尔夫6的横向稳定杆是通过套筒固定在车架上的，考虑实际安装情况，对横向稳定杆进行有约束的模态分析. 由于是约束模态，因此取前4阶模态分析对比，如表 4 所示.

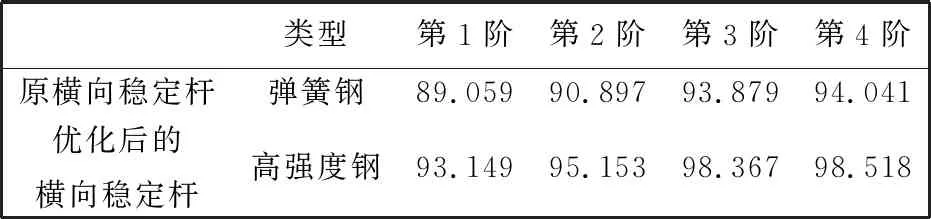
表 4 约束模态下的固有频率Tab.4 Natural frequency of constraint modal Hz

从表 4 可以看出，优化后的横向稳定杆在约束模态计算的固有频率和模态振型与原横向稳定杆基本相同. 因此与原横向稳定杆一样，不会发生共振现象[13].

4 扭转刚度分析

在汽车上，横向稳定杆会受到很大的扭力作用，当一侧车轮跳动时，横向稳定杆利用自身的扭转刚度来减小跳动以减少车身侧倾，因此扭转刚度是评价横向稳定杆的一个重要指标. 杆的两端分别施加Z轴正方向和Z轴负方向的大小相等的力，在套筒位置，除了ROTX不约束外，其余自由度均施加全约束，通过测出的扭转角度与扭转力矩进行拟合分析计算，得出横向稳定杆轻量化前后的扭转刚度. 在分析过程中，扭转力矩是作用在A,D点的Fa和Fd与力臂的乘积. 在ANSYS中，对稳定杆进行0～500 N的压力施加. 受力简图如图 12 所示.

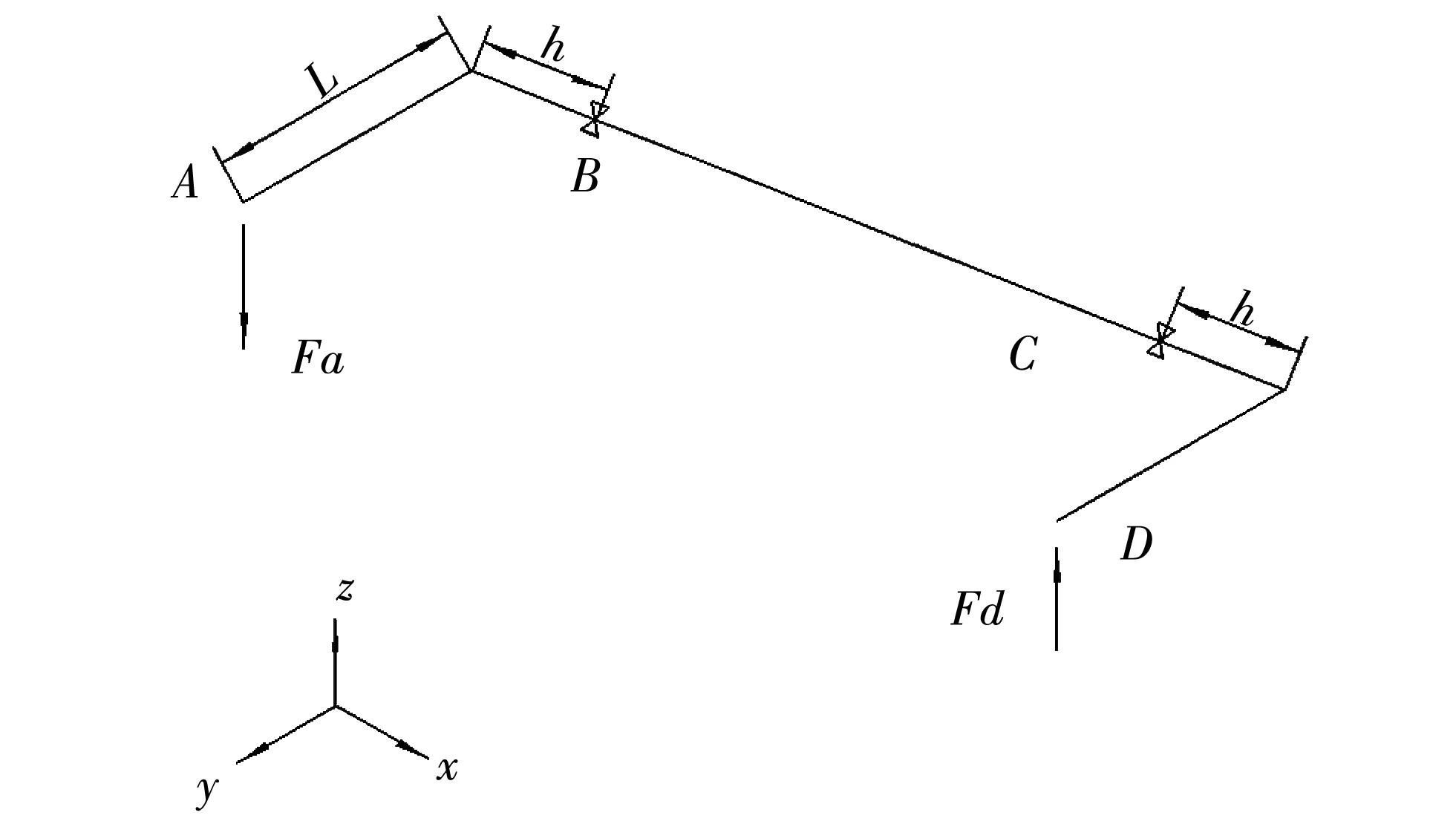
图 12 受力简图Fig.12 Force diagram

利用MATLAB拟合数据得到横向稳定杆的扭转角刚度图. 优化前后横向稳定杆的扭转角刚度如图 13 所示. 通过分析可知原横向稳定杆的扭转角刚度为 27 000 N·m/rad，优化后的稳定杆的扭转角刚度为 26 285 N·m/rad，优化后的扭转角刚度比优化前的要下降一些，这是因为对原横向稳定杆采用空心化的处理而造成的，但是仍然能够满足实际需要，因此轻量化设计合理.

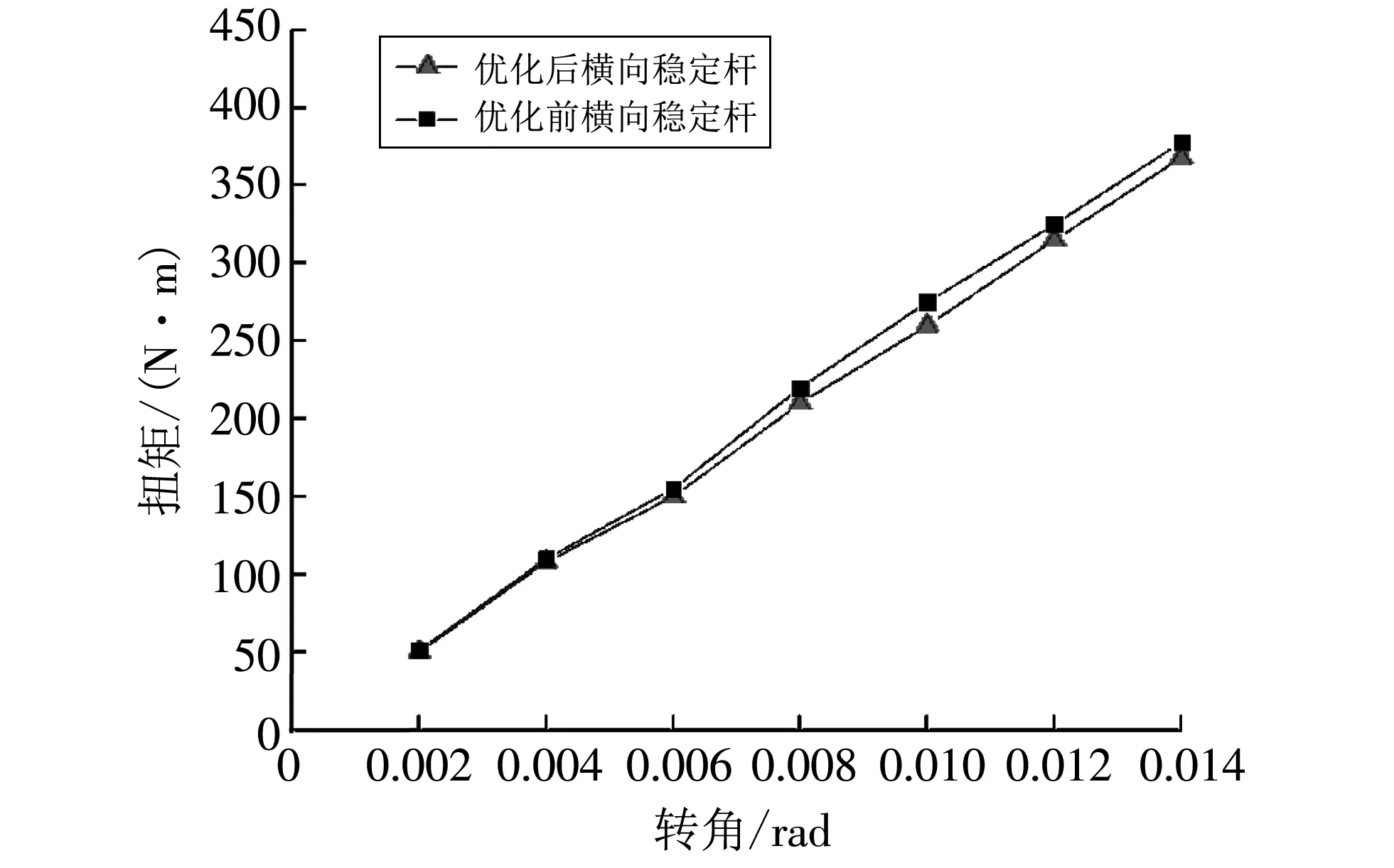
图 13 扭转角刚度图Fig.13 Torsional stiffness diagram

5 结 论

1) 对高尔夫6轿车前横向稳定杆进行轻量化设计，采用空心化的处理方式来减重，同时采用高强度钢来保证轻量化后的刚度. 验证结果表明在减重20%的情况下，稳定杆仍然满足实际要求.

2) 利用ANSYS对横向稳定杆进行两种工况分析，对比原横向稳定杆和优化后的稳定杆来验证轻量化设计的合理性.

3) 从自由模态和约束模态分析，验证了优化前与优化后的稳定杆振型和频率相差不大，不会引发共振问题.

4) 从扭转刚度的角度分析，得出了虽然优化后稳定杆刚度有所下降，但是仍然满足实际需要的结论，证明了横向稳定杆轻量化的设计合理.