基于改进EOQ模型的库存控制研究

□ 王 赛，陈 岩

(南京林业大学 经济管理学院，江苏 南京 210037)

1 引言

库存作为一种为满足未来需求而暂时闲置的资源，是管理者手中的一把双刃剑。库存不足，需要该存货进行生产的工人和设备就要停歇，造成供应中断；库存过多，却会掩盖生产或销售中的许多问题，比如，前序阶段生产速率下降，因为有存货积压后序阶段未受到影响，一旦存货消耗掉，才会发现前后生产速率不能匹配，过多的库存甚至会影响企业的资金周转。即便是在如今全渠道零售的环境下，研究重点也从渠道定价转变成了库存决策问题[1]。经济订货批量模型通过定量地分析库存费用的构成因素来求解最佳订货批量。本文意在对EOQ模型的部分假设做出适当改动，降低其理想化程度，在新的条件下寻求新的最优解。

EOQ模型理想的假设条件给学者们创造了巨大的研究空间。改变“需求率已知且为常量”的条件，黄世华等[2]在需求变化的之字形不确定分布条件下，以风险最小化为目标对EOQ模型进行修正；因高科技产品具有斜坡需求和延迟补货的特点，罗兵等[3]将其顾客按价格偏好者和时间偏好者分类，采用数值仿真分析了系统主要参数对销售商订货策略及总利润的影响；Chanda等[4]为出售技术产品的公司寻找需求随试验重复购买情况下的订货策略。改变“完美批次”的条件，王嗣琦[5]为模型引入了安全存货量进行修正，并证明了传统EOQ模型是修正模型的一种特殊情况；Salehi,Hossein等[6]提出了一个具有随机中断和部分缺货的EOQ模型，在由于质量问题或正常短缺导致供应链中断时，客户是否愿意等待下一批次交货，又因为批次存在缺陷的概率有限，所以检查批次后使用“全部接收或全部退回”策略，确定了最优库存成本及决策变量。考虑购置资金由借贷得到，张秀华等[7]建立新模型并寻求EOQ和JIT两种采购方式之间的成本差，并改变利息率的大小画出多条无差异曲线，发现年利息率越大，无差异平衡点的值越大，使得JIT在采购量较大的需求范围内成本更低；邹裔忠[8]为模型加入了贷款利率参数，为资金需求方确定了存货质押融资的最优定价策略。考虑库存品变质、成本损失问题，倪郁东等[9]在EOQ模型中考虑带有Taguchi成本损失下的最优成本，并且假定品质特性决定实际产品规格，品质特性服从产品规格的指数分布，按照Taguchi方法计算质量损失成本，进而分析年利润受品质特性的影响，发现年平均利润比EOQ模型中求得的值要小，而最佳订货量却高于EOQ；纪贤兵等[10]为模型加入了库存变质率参数，建立了多周期下生鲜农产品考虑变质的EOQ模型；陈杰等[11]建立多元马尔科夫需求预测模型，研究了易变质的多产品库存控制策略。

唐飞[12]认为在库存控制中，成本因素不是唯一的衡量标准，像如社会因素、环境因素也应被考虑其中，因而对EOQ模型进行了两种改进：一是将环境因素(碳排放、碳足迹、可持续性等)作为约束条件；二是将环境因素成本化。朱连燕等[13]针对需求率、一次订货费、单位维持库存费等不确定参数，结合径向基函数模型和稳健参数设计的思想，提出新的优化方法。EOQ模型多是在单一供需关系下被改进，而叶银芳等[14]针对单供多需的供应链关系，在需求为区间值的情况下构建EOQ模型并给出多个需求方进行成本分摊的博弈方法。Leopoldo Eduardo Cárdenas-Barrón等[15]在假定供应商为零售商提供贸易信用期的情况下，为零售商求得库存相关需求和维持库存费非线性的EOQ模型[16]。

通过阅读相关文献，发现学者在EOQ模型的改进上做了大量的研究工作。他们为模型能够接近更加真实的库存环境，将确定的参数变为不确定，或者增加新的参数进行限制，指导企业更加合理地进行订货，为库存管理提供了丰富的理论。本文的特色与创新主要体现在以下两个方面：模型改进上，双峰型需求变动的EOQ模型是针对产品的需求特性提出的，而维持库存费非线性的EOQ模型是分析实际库存环境下维持库存费与库存量的关系作出的，前者更具针对性，后者更具普遍性；模型构建上，双峰型需求变动的模型根据需求量关系式作出函数图像，而维持库存费非线性的EOQ模型先作出符合实际情况的曲线图像，再为图像找到合适的函数表达式。

2 EOQ模型改进研究

本文主要针对经典EOQ模型两条假设进行改进研究，分别改动并提出了双峰型产品需求变动的EOQ模型和维持库存费非线性的EOQ模型。

2.1 EOQ模型的基本假设和计算方法

EOQ模型有以下9个假设条件：

①外部对库存系统的需求率已知、需求率均匀且为常量；

②一次订货量无最大最小限制；

③采购、运输均无价格折扣；

④订货提前期已知，且为常量；

⑤订货费与订货批量无关；

⑥维持库存费是库存量的线性函数；

⑦不允许缺货；

⑧补充率为无限大，全部订货一次交付；

⑨采用固定量系统。

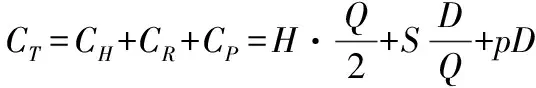
其中，模型所涉及到的字母及其表示含义如下所示：

CT，CH，CR，CP，CS——库存总费用，维持库存费，订货费，购买费，缺货损失费。

H——单位库存量一年维持库存费；

Q——最大库存量，Q*为最佳订货批量或经济订货批量；

D——年需求量；

S——一次订货费；

P——进货单价。

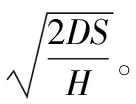
2.2 双峰型产品需求变动的EOQ模型改进研究

EOQ模型的假设①提出，外部对库存系统的需求率已知、需求率均匀且为常量。在现实生活中，企业里、市场上大部分物品或许能够基本保持稳定的需求量，可以适用此假设条件，而对于新上市的产品或季节性产品却并不适用。因为新上市的产品无法确定消费者对其接受程度，即使之前做过充足的市场调查，仍然存在客观原因譬如竞争者调价等非己方能够控制的因素影响实际需求量；而对于季节性产品来说，大部分存在需求量按年波动的规律，譬如空调、冰箱是双峰型产品，在夏季和冬季需求量较高，而围巾、手套等是单峰型产品，只在冬季有较高的需求量。

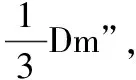
①考虑峰值下t的取值。

一年的12个月，人们常把3月、4月、5月定为春季，6月、7月、8月定为夏季，9月、10月、11月定为秋季，12月、1月、2月则是冬季。我们假定双峰型产品在6月末及12月末取得最高点，即函数在6、12处取得最大值，3、9处有最小值。

②确定ω。

③确定φ。

④确定A和k。

根据最大最小值可得二元一次方程组：

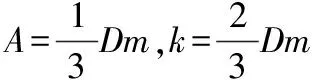
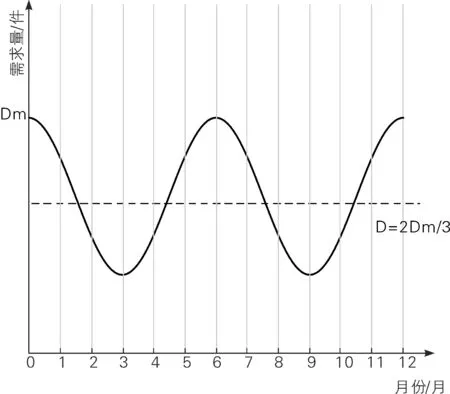
图1 双峰型产品月需求量变化图

我们寻求经济订货批量是通过使得年费用最小来做到，所以，在其他假设条件不变的情况下，再来看下年库存费用的表达式的变化。

在EOQ模型中，订货费和购买费都与D有直接关系。而在双峰型产品需求变动的情况下，要求得一年的总需求量，就要依次算出每个月的需求量再加和。这里有必要说明一点，虽然我们在作图时表现出来的函数图像是连续的，这样是为了方便观察，但实际上是它离散的。因为t取某一值时，它的含义是“在某月期间内，总需求量为多少”，因此t也只能取1-12之间的整数值。

现将1-12分别代入需求量关系式计算每月需求量经计算，年需求量为8Dm。

所以，在需求变动的模型下，年库存总费用为：

此时的经济订货批量：

2.3 维持库存费非线性的EOQ模型改进研究

EOQ模型的假设⑥提出，维持库存费是库存量的线性函数。其实，在现实生活中并非如此，为了维持最初的那部分库存量所需要的费用比较高，后来费用的增量会比库存的增量要慢，也就是每增加一单位库存量，所需要的增加的库存费用会逐渐减少，类似于经济学中的边际成本递减规律。所以，本文将EOQ模型的假设⑥改成“维持库存费不是库存量的线性函数，而是随库存量增加，边际维持成本会减小”。

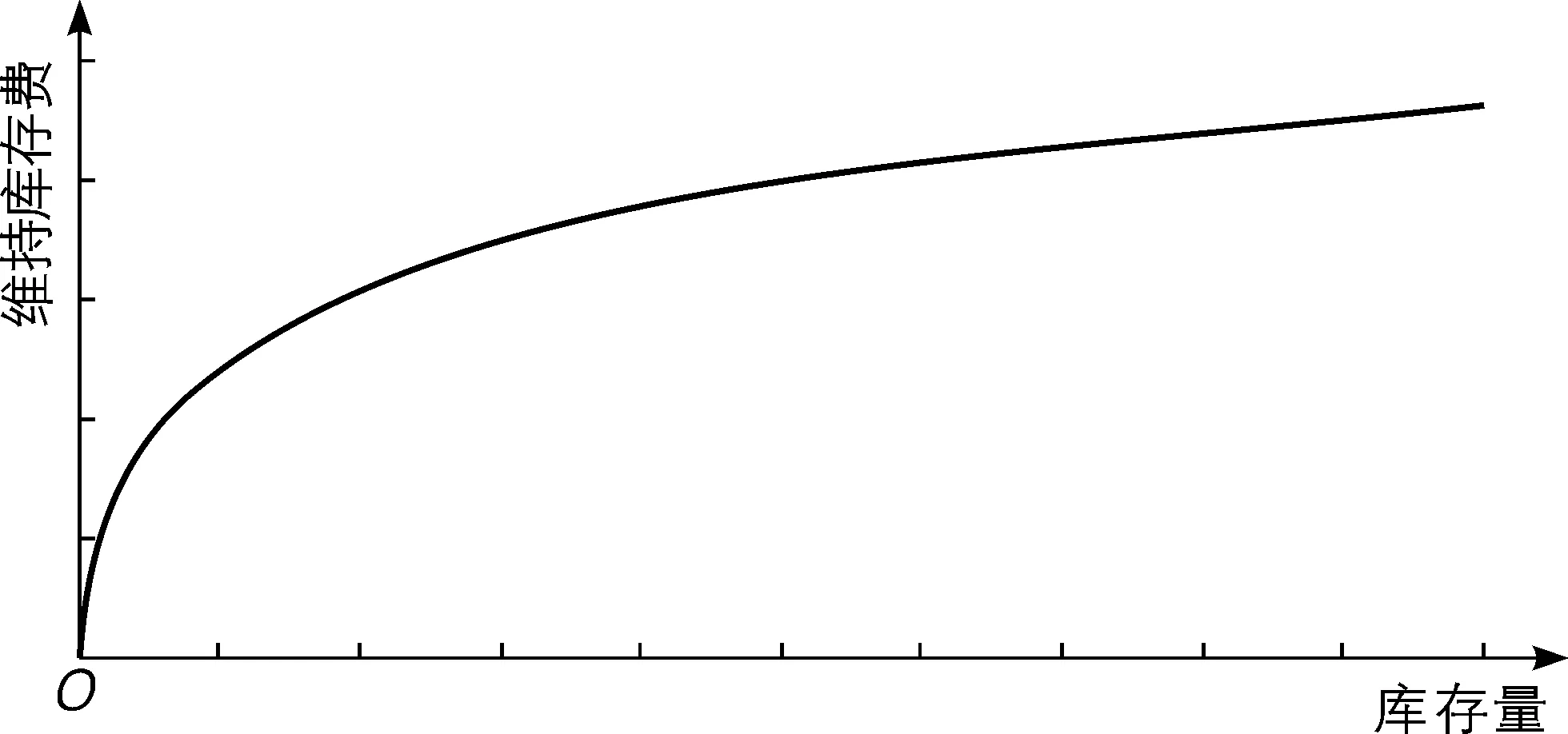
图2 实际维持库存费与库存量关系图

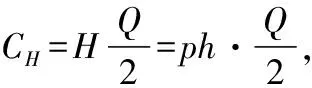
由于我们只对维持库存费即CH作了变动，其他假设条件没有改变，因此并不涉及CR和CP的变化。在维持库存费非线性模型下，年库存总费用为：

现将该函数对Q求导：

令其等于0，得到：

化简上述式子，得到一元二次方程：

kHQ2-SDQ-SD=0

因为：

Δ=S2D2+4kHSD>0

所以该方程存在两个不同的根。

用公式法求得方程的根为：

因为:

而库存量Q是非负的，所以方程的根即经济订货批量只能为：

3 模型应用算例

本文选用了某医院药房的两种药品作为改进模型的算例对象。其中，盐酸氯丙嗪片的需求具有双峰性质，是双峰型产品需求变动EOQ模型的算例对象；而维持库存费非线性的EOQ模型应用上具有普遍性，所以对选取算例对象要求不高，只是单价高的药品更能体现出新模型与原模型的订货批量差距，桔贝合剂较为合适。

3.1 双峰型产品需求变动EOQ模型应用

3.1.1 确定算例对象

本文选用需求具有双峰性质的药品——盐酸氯丙嗪片作为该模型的算例对象。该药品是一种抗精神病类药物，因精神病在春秋两季易发作，所以其需求存在双峰性质。虽然本文在建立双峰型产品需求变动EOQ模型时，峰期在夏季和冬季，而该药品是在春秋两季存在高峰，考虑到均是双峰型且不影响年需求量，所以直接用公式计算。

3.1.2 算例过程

假设药房在盐酸氯丙嗪片需求量最高的月份有832瓶，进货单价为9元，一次订货费为10元，H是由资金利息和仓储费由构成，且H=ph，其中h为资金效果系数，是资金年利息率和单位维持库存费占物品价值的百分比之和，假设前者为12%，后者为18%，所以h是30%，则ph即H的计算结果为2.7元。也就是每存储一瓶盐酸氯丙嗪片，一年需维持库存费2.7元，1000瓶需要2700元。

3.1.3 效果对比

现将盐酸氯丙嗪片应用经典EOQ模型和改进EOQ模型的各项库存费用作对比，如表1所示。

表1 盐酸氯丙嗪片应用改进前后模型费用对比表

观察表1，改进的EOQ模型订货批量略小于原模型的值，且降低了年库存费用。

3.2 维持库存费非线性EOQ模型应用

①确定算例对象。

由于该模型的提出是根据实际维持库存费与库存量的关系来的，为体现其与原模型的差距，本文选用进货单价较高的桔贝合剂作为算例对象。

②算例过程。

假设某药房有药品桔贝合剂，每月需求量为1486瓶，则年需求量是17832瓶，该药品的进货单价为33元，一次订货费为10元，h仍为30%。由于模型中还存在一调节系数k需被确定，所以现通过对年维持库存费用的分析来确定其值。

式子CH=kHln(Q+1)=kphln(Q+1)中Q是自变量，p、h已知，则ph即H的计算结果为9.9元。也就是在维持库存费与库存量之间是线性关系的情况下，每存储一瓶桔贝合剂，一年需维持库存费9.9元，1000瓶需要9900元。我们的模型指出，二者非线性关系，还需要kln(Q+1)来调节。调节的作用就是使得当Q=1时，年维持库存费远大于9.9元；当Q=1000时，年维持库存费远小于9900元。于是得到：

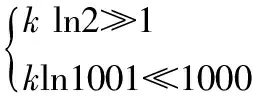
我们可以确定一个合适的k值20。在这种情况下，年维持一瓶需要137.24元，年维持1000瓶需要1367.93元。在实际应用时，也可通过对H的量化来确定更科学的取值。

那么，CH=198ln(Q+1)。

求导并令其一阶导数等于0得到方程：

198Q2-178320Q-178320=0

运用MATLAB对方程求解，得到方程的两根分别是901.6050和-0.9989，显然，经济订货批量Q*为902瓶。

③效果对比。

现将桔贝合剂应用经典EOQ模型和改进EOQ模型的各项库存费用作对比，如表2所示。

表2 桔贝合剂应用改进前后模型费用对比表

观察表2，应用改进模型得出的订货批量远大于原模型，这主要是因为原模型的假设是“维持库存费是库存量的线性函数”，而桔贝合剂单价较高故而维持库存费高，制约了订货量的上升，虽然在这样较小的订货批量下取得的年库存费用也少于改进模型，但仔细分析后，发现这些量还不够满足四天的需求，甚至可能无法满足订货提前期的需求，频繁进货明显会为管理人员带来更多的工作负担，再看改进后的维持库存费非线性的模型下，订货批量明显更为合理。

4 结论

在算例中，通过对比改进模型应用前后的年库存费用，可以肯定，改进的新模型拥有更加经济或合理的经济订货批量。目前只是对两种药品进行改进模型应用，如果扩大使用，将会为医院寻求到合适的库存控制策略。对于公立医院这样的非营利性机构而言，增加的流动资金可用于提高医疗设备、病房设施等；减少人员在库存管理上的工作量也可以增加服务患者的时间。

本文虽然给出了新的假设条件下经济订货批量的计算方法，但由于自身能力有限，改动之后不能确定在需求量变动时订货点如何计算，影响EOQ模型的长期应用。鉴于目前的研究有限，也无法考虑多假设条件变动时如何制定订货策略，有待进一步研究。