碳纤维复合材料温度场的研究

黎缘，彭超义，张文伟，谢明亮，周萍

（株洲时代新材料科技股份有限公司，株洲 412007）

1 引言

碳纤维因其比强度、比模量高、疲劳性能好等优异力学性能，广泛应用于航空航天、风力发电、汽车船舶的结构件。同时，碳纤维具有优异的电热性能，在风力发电领域用来防除冰，在室内装饰中用来作为电暖材料[1]，在混凝土道路中应用于去除道路冰雪[2]。国内外学者对于碳纤维复合材料的电热性能进行了广泛研究。Changliang Li[3]等对碳纤维复合材料不同功率下的温升情况进行了研究，发现通电初期温升率最大，随后温升率逐渐减小，温度达到一个恒定值。功率越大，达到平衡温度值越大。丁海滨[4]等对碳纤维织物电阻性能进行了研究，发现碳纤维织物的电阻与碳纤维织物的长度呈线性增加关系，与碳纤维织物的宽度与铺层呈非线性减小关系，浸入树脂后的碳纤维织物电阻略有减小，通常可以忽略不计。谢明亮[5]等研究了碳纤维复合材料在不同力学载荷下的电热性能，发现碳纤维复合材料的电阻与温度的升高成线性减小关系，但变化较小。电阻值随拉伸载荷增大线性增加，在初始加载和即将拉断时电阻有较大波动，电阻在弯曲载荷作用下初始加载时没有明显变化，当达到临界值时呈线性增加。韩志勇[6]等测试了碳纤维复合材料通电后的表面温度并使用ABAQUS 软件对其温度进行模拟，实验值与模拟结构吻合较好。目前，已有文献中关于连续碳纤维复合材料电热性能的研究主要集中在试验和初步的模拟分析，对碳纤维复合材料加热后温度场的研究不够深入。

本文用手糊袋压工艺制备了多种带电极的碳纤维复合材料板，采用微欧计测量试样的电阻值，通过红外热成像仪采集了完好模型碳纤维复合材料、含孔洞损伤、重叠模型的温度场分布。建立了准各向同性碳纤维复合材料板电阻数学模型，可准确预测样板电阻值。同时，采用有限元软件模拟了上述实验的温度场分布，并进一步研究了碳纤维复合材料形状、重叠搭接、圆形孔洞损伤、长宽比等对温度场的影响。

2 碳纤维电热复合材料的实验部分和数学模型

2.1 原材料和设备

表1 实验部分使用原材料表Table 1 Raw material used in experiment

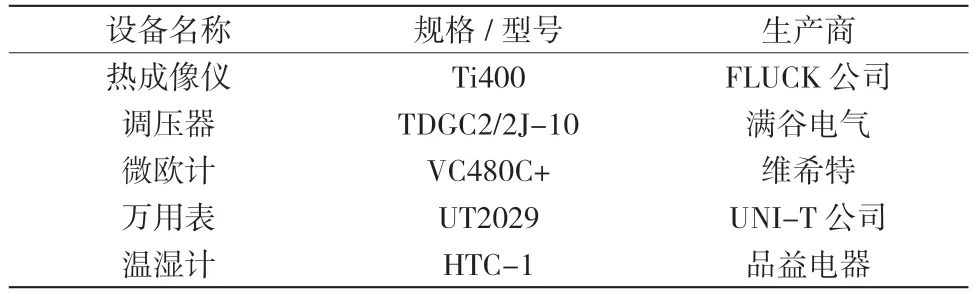
表2 实验部分使用设备表Table2 Equipment used in experiment

2.2 试验制备与测试

将面密度200g/ cm2碳纤维[±45]双轴布浸渍陶氏2014A/B 树脂手糊固定在一层4mm 厚的玻璃钢材质平板上，距碳布两端50mm 处用5mm 宽的导线铜丝带外接电极，导线铜丝带同铺层结构见下图1 所示，其中铜带间有效碳布尺寸为160mm×80mm。然后，对试样进行密封并抽真空处理，同时按照70℃/5h+25℃/12h 制备成样。脱模清洁处理后，用微欧计测量导电铜丝带两端电阻，将标定准确的调压器连接导电铜丝带并接通电源，同时用红外热成像仪实时采集试样表面温度，采集频率为每30s 一次。

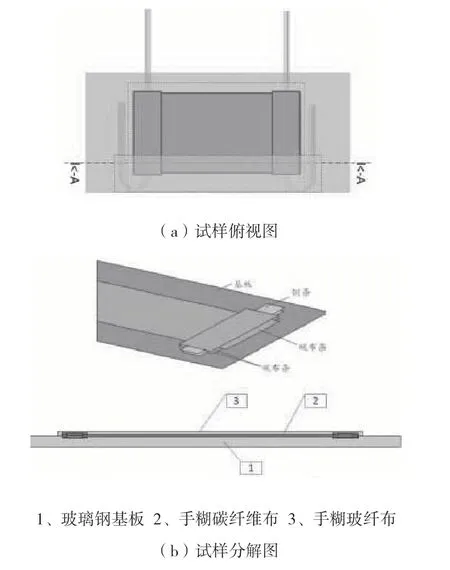
图1 试样结构Fig.1 Structure of specimens

2.3 碳纤维复合材料电阻的数学模型

碳纤维复合材料的电阻值与施加其上的功率成反比，电阻值与其温度场的最高温度紧密关联。应用的碳纤维复合材料为[±45]，为准各向同性，面密度为200g/m2，理论厚度约0.2mm。假设碳纤维复合材料为各向同性导电膜状电热材料。导电膜的导电能力一般可以用方阻来表示，即长与宽相等时电阻值Rsq，方阻的大小只与材料自身的特性即其厚度有关，对于均匀等厚度的同一种材料，其方阻可以看作一致。矩形导电膜，假设其宽度为W，长度为L，则其等效电阻为，可以看出导电膜电阻大小与长宽比成正比。从公式可知，长宽比一定的均匀等厚度碳纤维，其电阻值恒定。

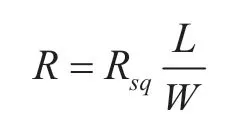
当导电膜之间的距离按f(x)规律变化时，可把导电膜分为宽dx，长为f(x)的无限个单元，这些电路的电阻值分别为

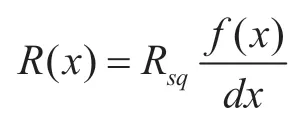
因此，总电阻为无限个并联的电阻单元求和得到

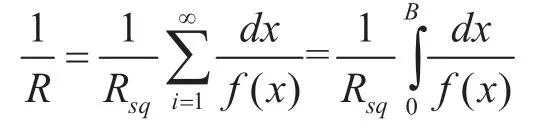
通常可以通过改变碳纤维复合材料的形状来调整不同区域的功率密度。一般的采用梯形形状来改变碳纤维复合材料两端的功率密度。假设梯形的上底长为L1，下底长为L2，高为W，方阻为Rsq,则在x 处L(x)为

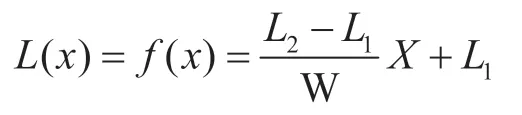
将上式代入前一式得

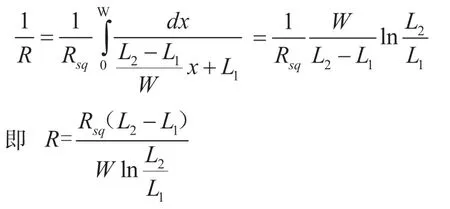
测量试验试样电阻值为0.48Ω，利用数学模型计算电阻值为0.50Ω，两者相差4.17%，数学模型可以较准确用来预测电阻值，以用来指导CFRP 板的设计。

3 碳纤维电热复合材料有限元建模与验证

以试样的尺寸为基础，基于有限元分析方法建立了与试样等尺寸的有限元模型（完好试样有效面积：160mm×80mm），在有限元模型长度方向上两侧施加与试验测试时负载电压一致的电压，设置环境温度为25℃、对流系数为12.5W/(m2·K)、电阻率为0.00005Ω·m、导热系数为0.56W/(m·K)，对有限元模型进行电-热耦合分析。

对比有限元结果与试验结果可以发现，试验测试云图与有限元计算云图非常吻合，见图2 和图3。云图在试样边界处出现温度差异，而在试样中间位置试样的温度比较均匀，这是由于边界散热导致。其中试验测试最高温度为117.6℃，有限元计算最高温度为120℃，两者差异为2%。

图2 试验测试温度云图Fig.2 Temperature field of experiment

图3 有限元计算温度云图Fig.3 Temperature field of Finite Element Method

采集试样通电过程中最高温度与时间的关系，采用瞬态计算方法计算有限元模型最高温度与时间的关系，可以发现两者非常一致（如图4 所示），表明采用有限元软件可以有效模拟叶片的温度场。随着通电时间的加长，碳布产生的焦耳热越来越多，而同时碳布自身会对与周围的基体发生热传导，当两者达到平衡时，曲线逐渐趋于平衡。

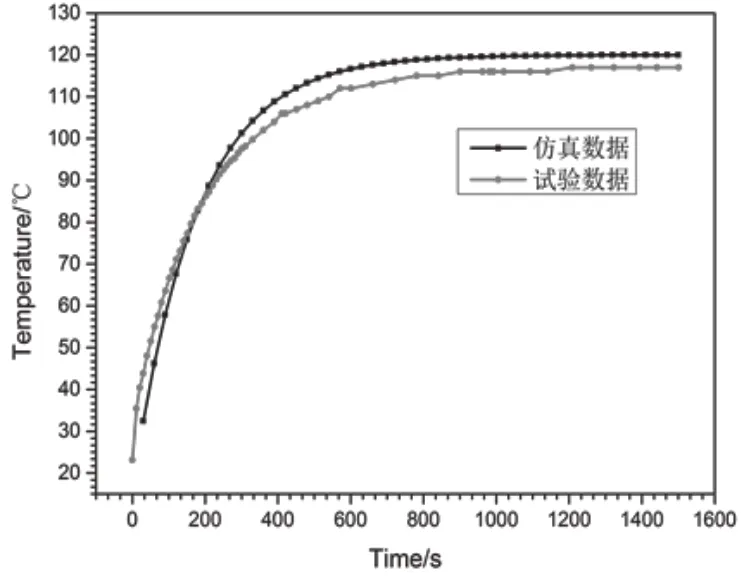
图4 最高温度值—时间曲线对比图Fig.4 Comparison of highest temperature-time curve

4 碳纤维电热复合材料温度场的影响研究

4.1 形状对温度场的影响

由模型计算可知，通过改变碳纤维复合材料的形状可以改变电阻。本论文研究了等腰梯形和直角梯形温度场分布，为碳纤维复合材料功率密度设计提供理论依据。等腰梯形和直角梯形的下底长为0.12m，上底长为0.04m，对比两梯形碳纤维电热复合材料的温度云图见图5 和图6，可以发现等腰梯形在大于90°的尖角处，会存在局部高温点，且直角梯形的高温点比等腰梯形的高温点高的多。通过使用梯形形状可以改变电热材料的温度场，使梯形上底和下底两侧温度存在一定温度梯度，尤其在风力发电机叶片的碳纤维加热区域的设计中，可以采用梯形的形状进行温度布局的改变。改变等腰梯形上下底边的长度可以发现，大于90°的钝角越大，其局部高温点越高。因此，在碳纤维布局设计时，应减小倾斜角度，平衡功率密度布局分布与局部高温区域的关系，选取合适的碳纤维形状和尺寸。

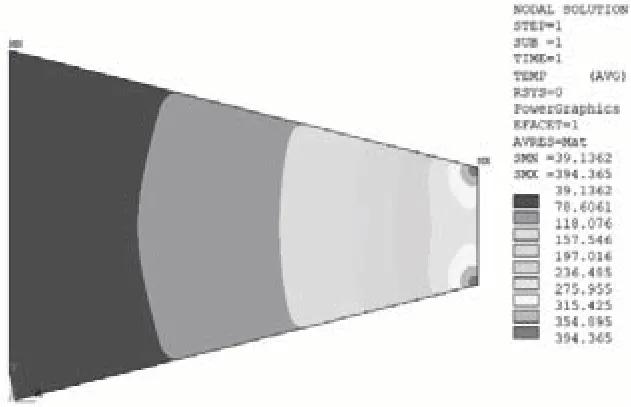
图5 等腰梯形样件温度云图Fig.5 Temperature field of isosceles trapezoid sample

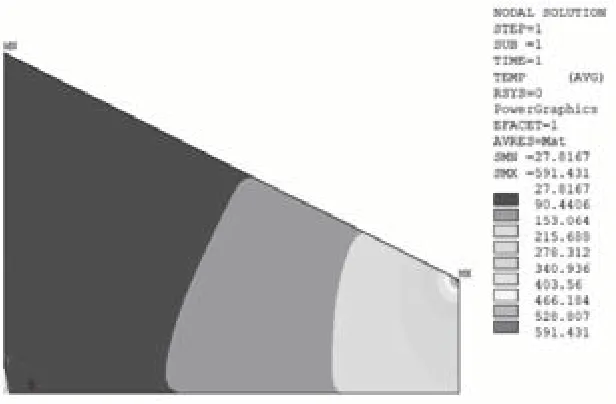
图6 直角梯形样件温度云图Fig.6 Temperature field of right trapezoid sample

4.2 重叠对温度场的影响

由电阻公式可以知道，改变碳纤维复合材料的厚度，也就是改变碳纤维铺层厚度，可以改变碳纤维复合材料功率密度。研究了碳纤维布在长度和和宽度两个方向上碳布堆叠情况下的温度场分布。碳纤维布的尺寸为0.16m×0.08m，其中将长度方向进行重叠。分别在长边A 和B 面和短边上C 和D 面施加电压。调整重叠位置的尺寸大小，并利用路径映射法采集横截面上的节点温度，如图9 所示。图7和图8 分别为重叠搭接10m 和50mm 温度云图，可以发现，在短边面C 和D 施加电压时，重叠区域的碳布类似于并联，重叠区域的温度明显高于其他位置。随着搭接尺寸的增加搭接区域的最高温度增加，除冰的效率将增加；但搭接尺寸的增加，试样的温差也进一步增加，因此需要合理布置搭接尺寸来提高叶片的抗冰效率，在风电叶片碳布除冰时，叶尖和前缘合膜缝附近等区域由于对流换热系数高等，需要增加热量以抵消对流过程损失的能量，采用并联重叠碳布的方式可达到上述目的。而在长边面A和B 施加电压时，在重叠区域位置明显的温度偏低，且重叠区域越大，温度越低。因此，可以通过增加串联的重叠位置来减小局部区域的温度。例如风电叶片采用碳纤维布在叶片外表面铺设加热材料时，PVC 和Balsa 木处，由于导热系数低，向叶片内热传导的热量低，可以减小此区域的能量，可以采用串联重叠的方式增厚碳布面积。

图7 重叠搭接10mm 温度云图Fig.7 Temperature field of overlapping with 10mm

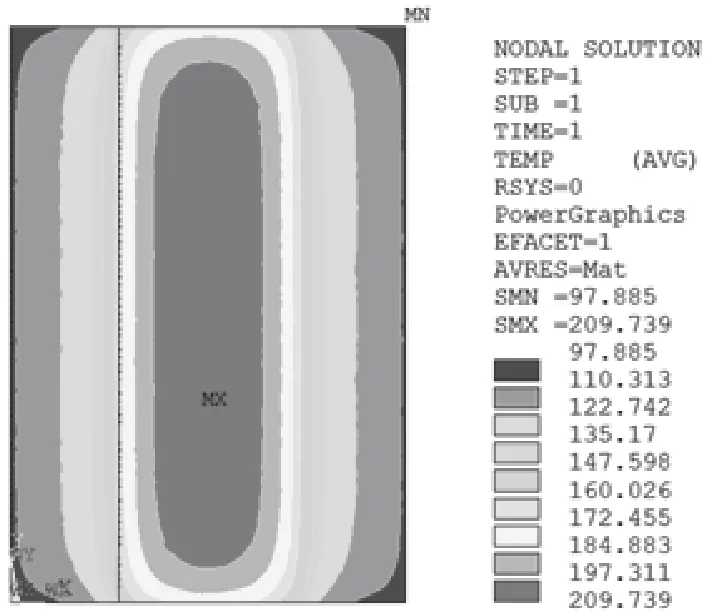
图8 重叠搭接50mm 温度云图Fig.8 Temperature field of overlapping with 50mm

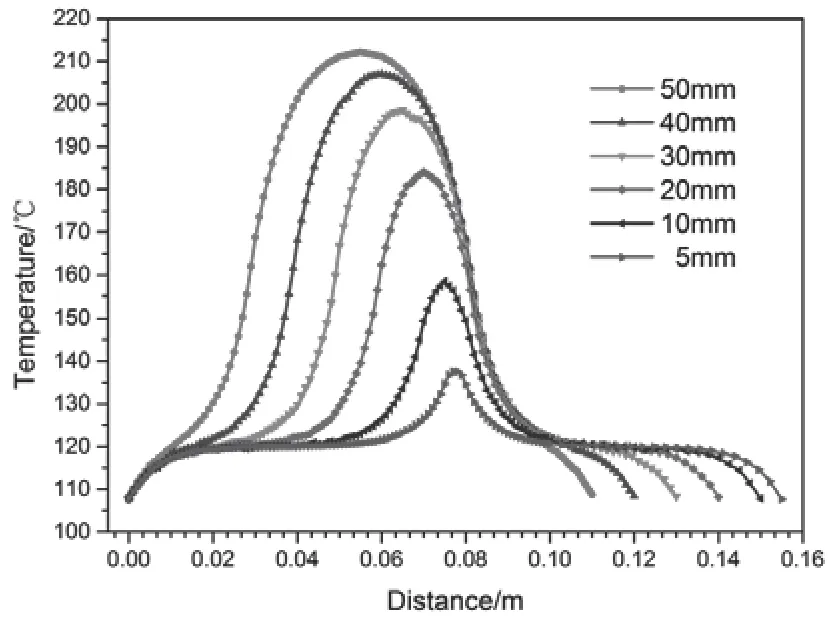
图9 重叠搭接样件长度中心线截面温度Fig.9 Section temperature of overlapping sample along the length direction center line

4.3 孔洞损伤对温度场的影响

风电叶片在运输和制造过程中，可能会遭遇孔洞损伤。在碳纤维板模型中，制造了不同直径的圆形孔洞损伤。对比圆形孔洞试验云图和有限元云图，见图10-图15 所示。从图可以看出试验云图与仿真云图最高温度位置基本一致，都出现在圆形孔洞的横向位置附近。虽然随着孔径的增大最高温度值仿真结果存在差异，但升高趋势和位置基本一致。从结果可以看出，小孔对碳布周围区域的温度影响较小。因此，在碳布受到较小的孔洞损伤时，可以暂不修复，但当孔径直径占碳布通电截面的尺寸太大时，将会在孔洞附近产生显著高温区域，需要修复处理。

图10 4mm 孔洞损伤试验温度云图Fig.10 Experiment Temperature field of the circular-hole damage with 4mm

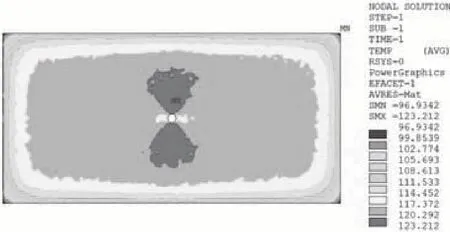
图11 4mm 孔洞损伤仿真云图Fig.11 FEM temperature field of the 4mm circular-hole damage

图12 20mm 孔洞损伤试验温度云图Fig.12 Experiment Temperature field of the 20mm circularhole damage

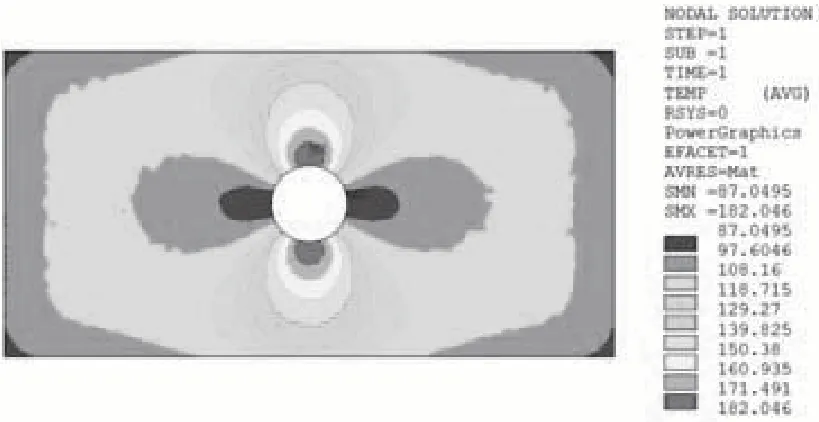
图13 20mm 孔洞损伤仿真云图Fig.13 FEM temperature field of the 20mm circular-hole damage

图14 40mm 孔洞损伤试验温度云图Fig.14 Experiment Temperature field of the 40mm circularhole damage

图15 40mm 孔洞损伤仿真云图Fig.15 FEM temperature field of the 40mm circular-hole damage

采用路径映射的方法提取孔洞损伤样件长度中心线截面上节点的温度，见图16。可以发现，随着孔径直径的增大，试样的最高温度和温差均增加；当碳纤维复合材料的温度太高时，会对其树脂基体的疲劳性能产生负面影响，甚至当温度增加到一定程度时树脂会发生失效，因此需要根据孔径损伤尺寸选择有效的修补方法。

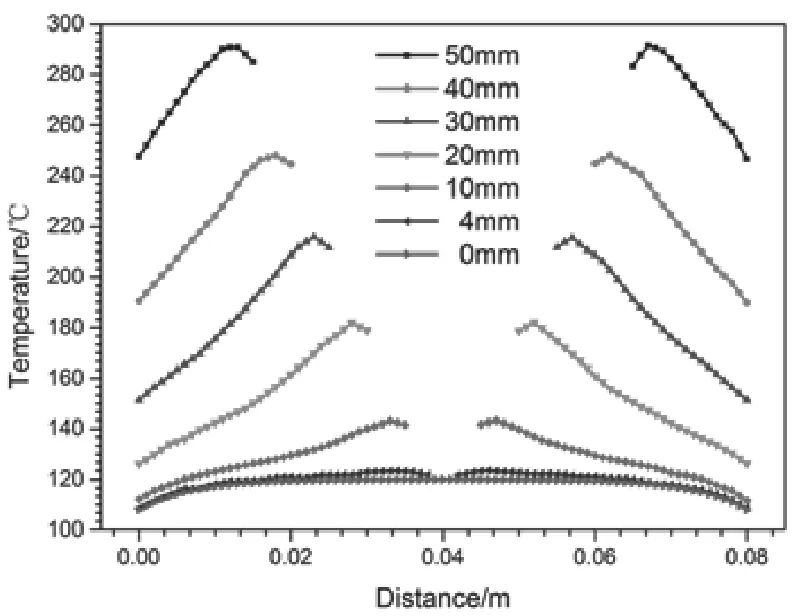
图16 孔洞损伤样件长度中心线截面温度Fig.16 Section temperature of circular-hole damage sample along the length direction center line

4.4 长宽比对温度场的影响

为进一步验证理论数学模型中长宽比一定情况下的加热情况，固定长宽比为2，分别调整碳纤维复合材料的长为0.16m、0.20m、0.32m、0.40m 长度下温度场，可以发现长宽比一定的情况下，改变长度或宽度对碳纤维复合材料的温度场几乎没有影响。

5 结论

1）[±45]准各向同性的碳纤维双轴布可以近似处理为各向同性材料，建立数学模型计算了碳纤维复合材料的电阻，以数学模型为基础，得到了改变碳纤维复合材料功率密度的方法以及梯形CFRP 板电阻的计算方法。

2）制备了碳纤维复合材料试样，通电后用红外热成像仪记录了试样表面的温度分布。采用电热耦合方法，建立碳纤维复合材料加热模型，对比试验和仿真的结果，发现两者数据基本一致，最高温度差异约为2%，表明可以采用此模型进行碳纤维复合材料温度场的仿真，分析差异的来源主要在于模型没有建立后面玻璃钢基板，没有考虑碳纤维通过热传导温度的传递，近似处理为与空气的对流传热。

3）比等腰梯形和直角梯形的温度云图，发现等腰梯形在大于90°的尖角处，会存在局部高温点，且直角梯形的高温点比等腰梯形的高温点高很多。改变等腰梯形上下底边的长度可以发现，大于90°的钝角越大，其局部高温点越高。因此，在碳纤维布局设计时，应减小倾斜角度，平衡功率密度布局分布与局部高温区域的关系，选取合适的碳纤维形状和尺寸。

4）随着搭接尺寸的增加搭接区域的最高温度增加，除冰的效率将增加；但搭接尺寸的增加，试样的温差也进一步增加，因此可以合理布置搭接尺寸来提高叶片的抗冰效率。

5）随着孔径直径的增大，试样的最高温度和温差均增加；但复合材料的疲劳性能会随着温度的增高而有所下降，当温度增加到一定程度时树脂会发生失效，因此需要控制制造过程中的孔径尺寸，且需要根据孔洞的相对大小选择有效的修补方法。