基于新型振型函数的渐细变截面悬臂梁的自由振动理论与实验研究

周坤涛，杨 涛，葛 根

(1.天津工业大学机械工程学院，天津 300399；2.天津理工大学工程训练中心，天津 300384)

变截面悬臂梁的振动在工程中有着广泛的应用，近年来被集中应用于微机电系统[1-2](MEMS)和振动能量收集系统[3-4]。变截面梁的振型方程和等截面悬臂梁[5]有着根本性不同。由此导致的振动固有频率以及大振幅下的非线性特征也有巨大的差别。

目前，主要有四大类方法计算变截面悬臂梁的模态函数和固有频率。

1) 采用摄动法的思想。在均匀悬臂梁的振型函数的基础上摄动，将变截面悬臂梁分成相互连接的若干段的组合，将每一小段近似等截面悬臂梁的叠加，从而得到新的频率[6-8]，显然无论频率还是变形程度都不理想。

2) 利用有限元(FE)半解析法。该方法采用有限元(finite element)模拟出振型图形，再用多项式函数逼近此振型图像以此作为振型函数进行计算[9]，此方法对于一些复杂结构来说较有优势，但对于简单构件且要求精度的非线性振动而言，FE失之繁琐。

3) 采用瑞利-里兹法，通过选取满足边界条件的预设振型函数(通常还是均匀悬臂梁的振型函数)，不断修改项数直到频率收敛[10-11]，此方法求固有频率尚可，当用伽辽金法时空分离时，由于振型函数的不吻合，对变形的预测能力较差。

4) 无须近似逼近，直接将方程的解设为特殊函数，如贝塞尔函数[12-13]和Meijer-G函数[14]。文献[14]中，作者通过将振型函数视为四个Meijer-G函数的线性组合，研究了变截面悬臂梁的线性自由振动，然而该方法在求解振型函数的系数时可能是复数，导致画振型图不便。

针对以上研究现状，本文提出一种超几何函数及Meijer-G函数的线性组合的振型函数。并用有限元、有限元半解析法与实验验证该模态函数的精确性。随后考虑了变截面不可伸缩悬臂梁的非线性振动方程，探讨变截面梁在大振幅下的自由振动幅频关系，通过实验验证本文采用的模态函数无论在求解频率还是在预测振幅方面的有效性。

1 模型建立

1.1 动力学建模

如图1(a)所示，该欧拉-伯努利梁为等厚度且沿长度方向逐渐变窄的悬臂梁，长度为L，厚度为h，固定端和自由端的宽度分别为wA和wB。建立图示直角坐标系，x轴位于梁的中性轴，y轴沿梁厚度方向，z轴沿梁宽度方向，s轴为沿梁长度方向固定在中性轴上的弧坐标。图1(b)为坐标s处微段ds的变形图。

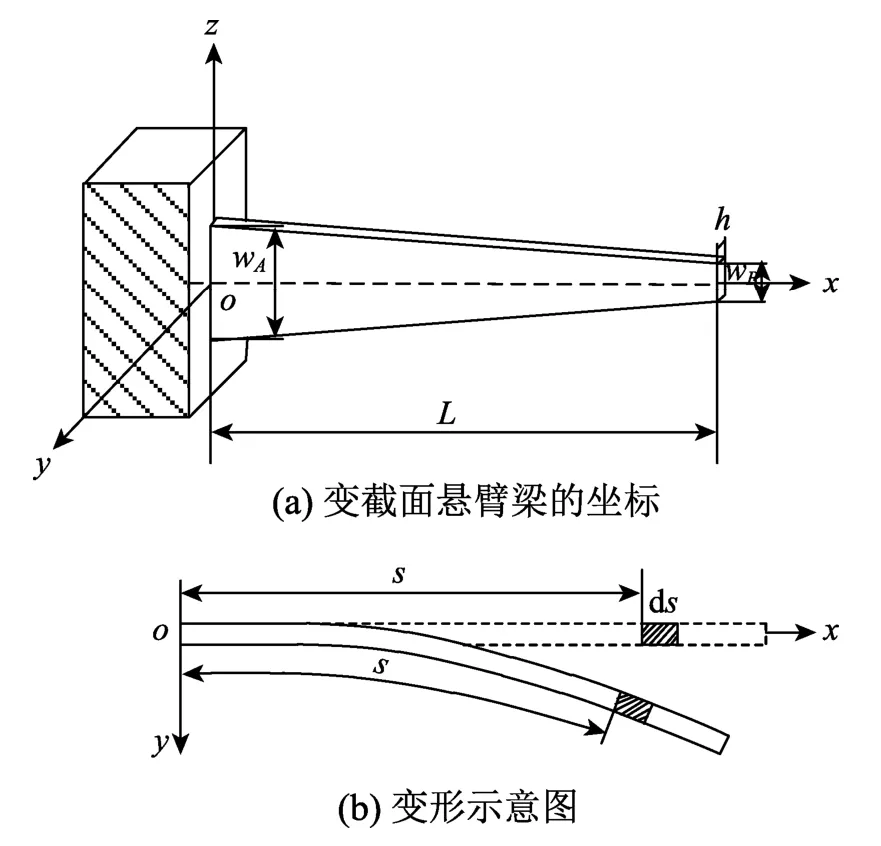
图1 欧拉-伯努利梁理论Fig.1 Euler-Bernoulli beam theory

定义截面形状参数p=1-wB/wA，则其随长度变化的横截面积和截面惯性矩分别为A(s)、I(s)，表示如下[14]：

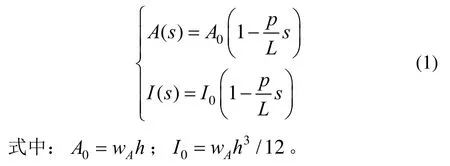
选取图1(b)中的微元段进行变形与受力分析，如图2所示，其中x、y为直角坐标系，ξ、η为自然轴系。图2(a)所示微元变形包含沿x轴的位移u、沿y轴的位移w以及微段的转角θ3。根据变形前后梁的微段几何关系可得：

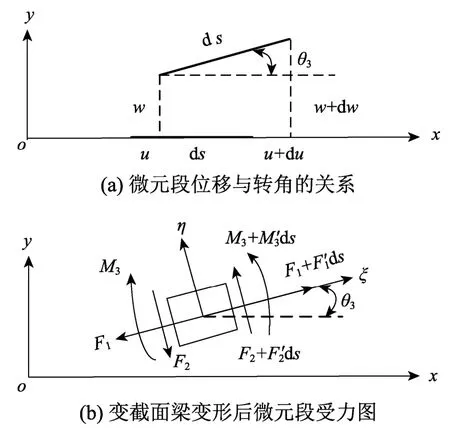
图2 微元段几何变形与受力图Fig.2 Differential element geometric deformation and free-body diagram

( ′ )表示对s的偏导数，(·)表示对时间t求偏导。因悬臂梁无轴向载荷，由图2(b)中受力分析可知，在s=L处满足(微段在x方向合力为零)[15]：

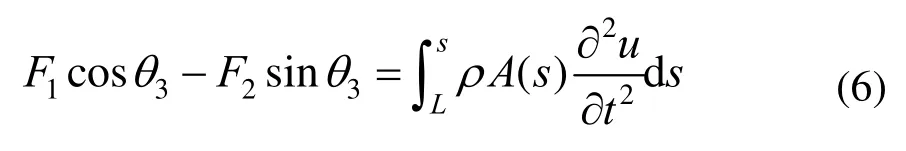
式中：F1为轴力；F2为剪力；ρ为梁的密度。

根据剪力方程可得[15]：

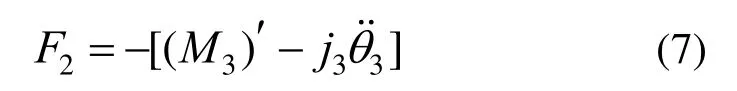
式中：弯矩方程M3=EI(sin-1w′)′，E表示弹性模量，为惯性矩；为梁横截面绕z轴的转动惯量，由于运动过程中，梁的转动惯性项明显低于横向振动情况，故本文忽略梁截面的转动效应(j3=0)。

y方向微分形式的平衡方程为：

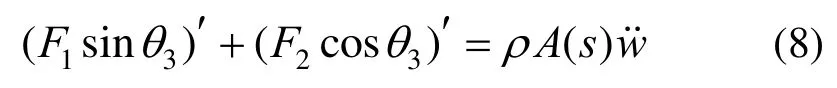
将式(6)、式(7)代入式(8)，并将方程进行Taylor展开，保留w非线性部分至最高三次方得到梁的非线性自由振动偏微分方程如下：

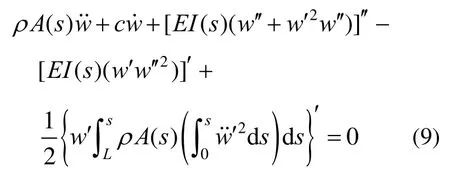
假设第i阶梁的位移可表示为：

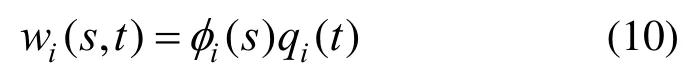
式中：φi(s)为暂时待定的模态空间分布函数；qi(t)为模态坐标。引入无量纲变换：

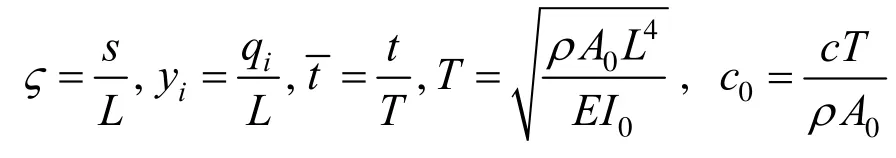
则式(9)转变为：

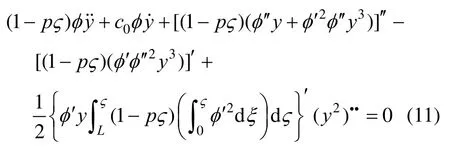
1.2 基于超几何函数和Meijer-G函数的振型函数

为求解梁的模态频率和振型，首先计算线性特征值问题，并令式(9)中阻尼项和非线性项系数为零，得到变截面梁无阻尼线性微分方程：

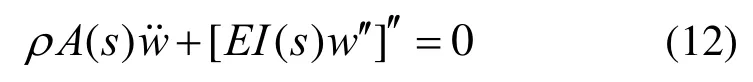
考虑悬臂梁的边界条件，固定端约束处即s=0时挠度与转角分别为零；在自由端即s=L处，弯矩与剪力分别为零，即：

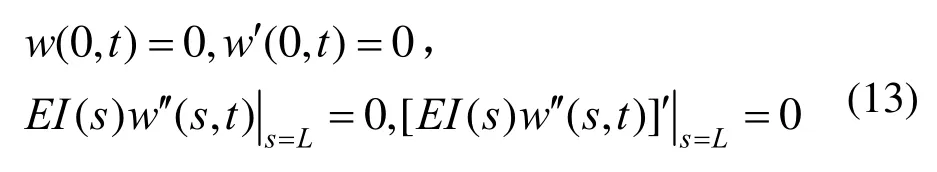
采用上述相同的无量纲变换，将式(10)代入式(12)可得：

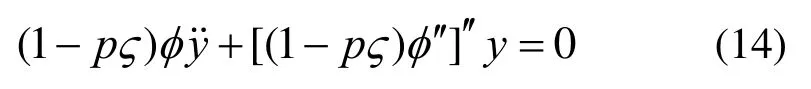
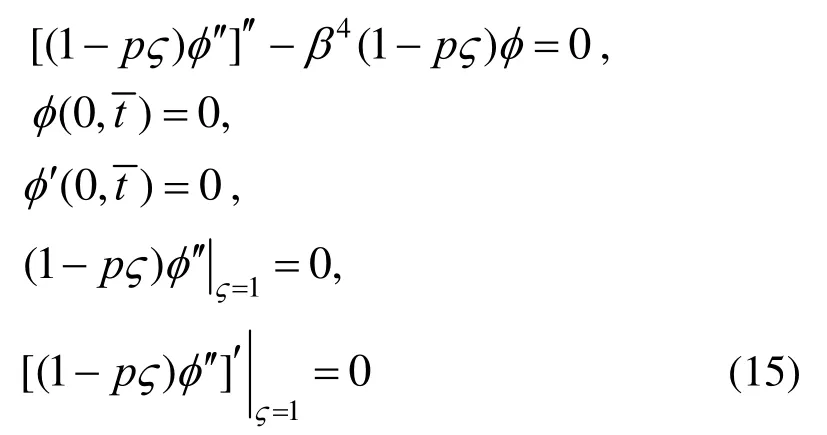
本文采用超几何函数和Meijer-G函数的线性组合形式来表达振型函数，如下：

式中，Cji(i=1,2,…,n)为待定系数：

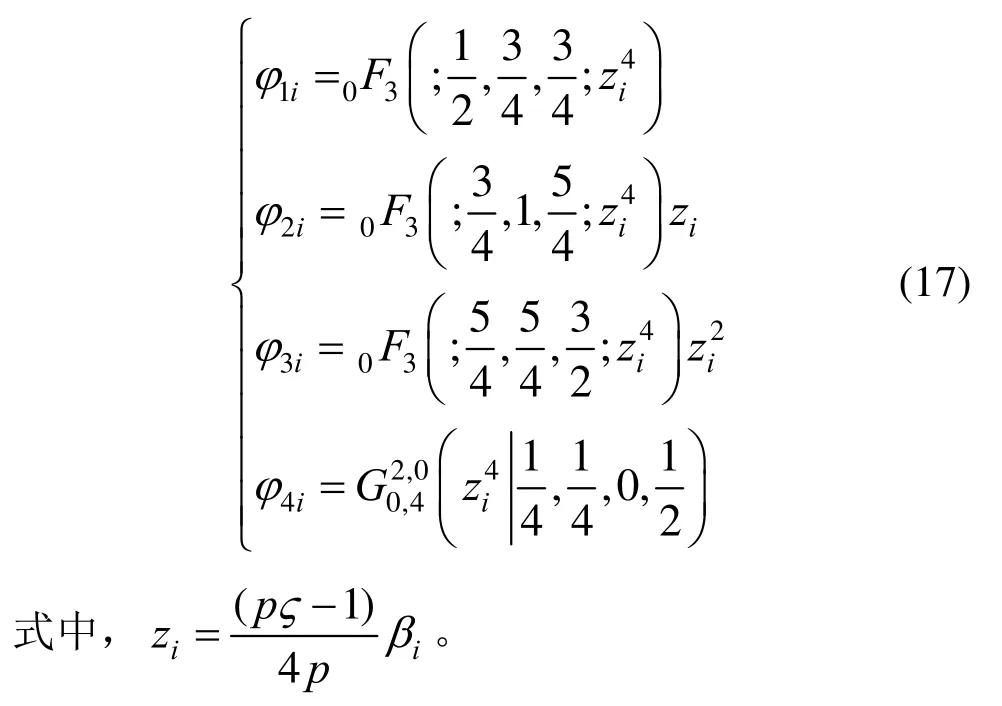
超几何函数pFq[13]和梅哲G函数[14]定义如下：

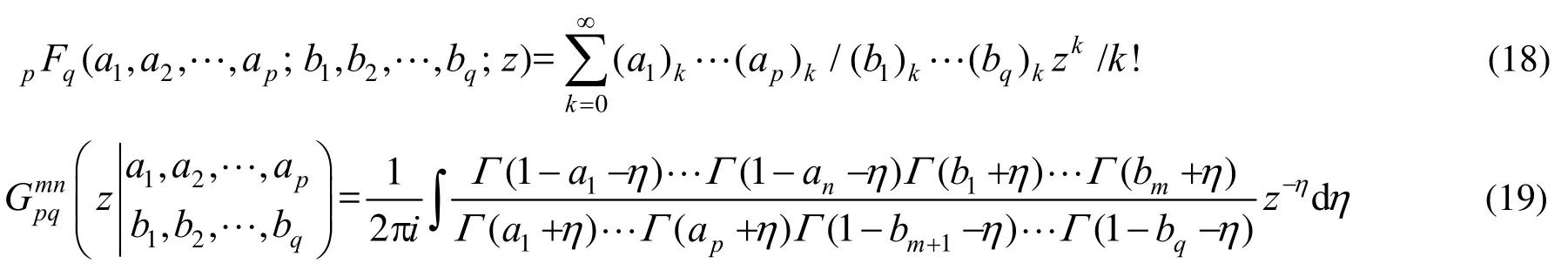
式中：z为独立自变量；a1-ap和b1-bq均为实常数。梅哲G函数中η为一个复变量，m、n、p、q为满足0≤m≤q, 0≤n≤p的整数，Γ()表示欧拉Gamma函数。

这里需要注意的是，这种振型函数和均匀悬臂梁振型函数有着根本性不同，均匀悬臂梁振型函数如下：

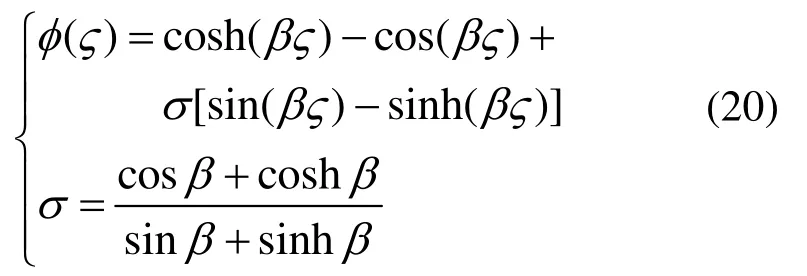
显然式(20)由三角函数和双曲函数线性组合而成，但式(16)由超几何函数和梅哲G函数线性组合而成。

为确定待定系数Cji和βi，需考虑式(15)后的四个边界条件。

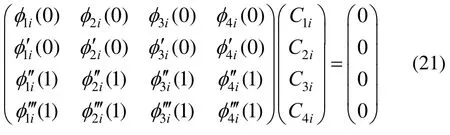
想要式(21)有非零解，必须使系数矩阵的特征行列式等于零，即可求得待定的βi。固定Cji中的任何一个，可求解出另三个。通过归一化条件可以确定这四个常数Cji。本文选取了p=0.3,0.5,0.7三种情况作为例，前两阶振型的系数Cji和βi，得到了一、二阶固有频率，模态振型。

1.3 理论分析

1.2节已经确定了振型函数φi(ς)，采用伽辽金法对式(11)进行时空分离：对各项乘以φ沿着无量纲量程梁长对ς从0到1积分，则式(11)可以重新表达如下：

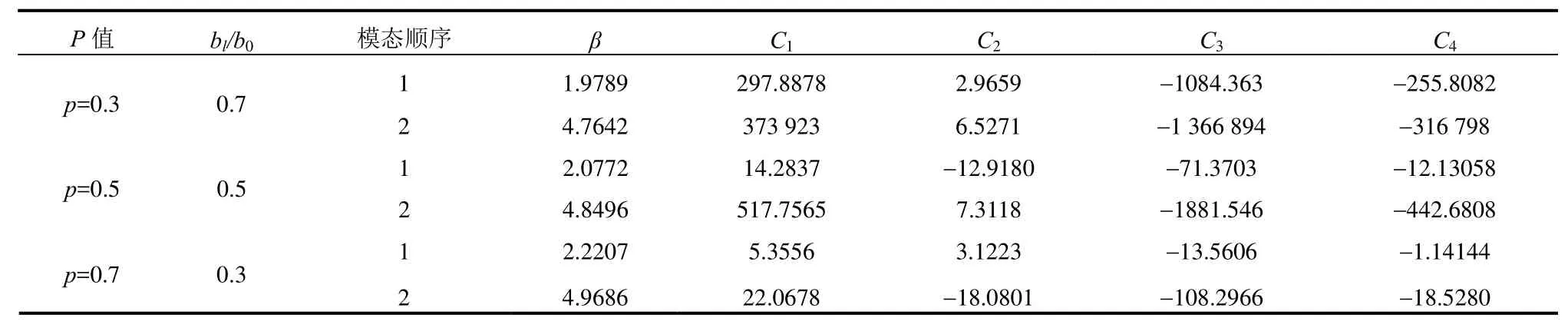
表1 前二阶模态的系数βi和CjiTable 1 βiand Cji coefficients of the first two modes

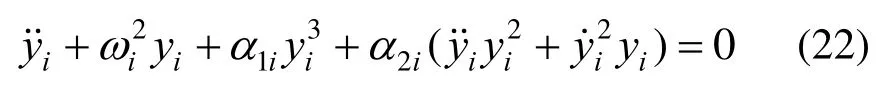
式中：ωi表示无量纲的固有频率；α1i表示无量纲弯曲非线性项系数；α2i表示无量纲惯性非线性项系数，具体参数如下：

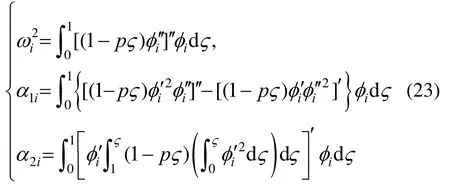
形如式(22)的方程在以往的等截面悬臂梁非线性振动中极为常用。但在变截面悬臂梁的变形系数p的不同取值下，无量纲的频率、弯曲非线性系数、惯性非线性系数取值各不相同。众所周知，弯曲非线性系数导致渐硬特性，惯性非线性系数导致渐软特性。这两项对研究非线性振动极为重要。而式(23)中三项系数都由振型函数的积分而来，因此只有足够精确的振型函数才能得到足够精确的非线性系数，本文振型函数代入式(23)得到的非线性系数如表2所示。反之如果验证这些系数的有效性也就充分说明了本文采用的振型函数的正确性。

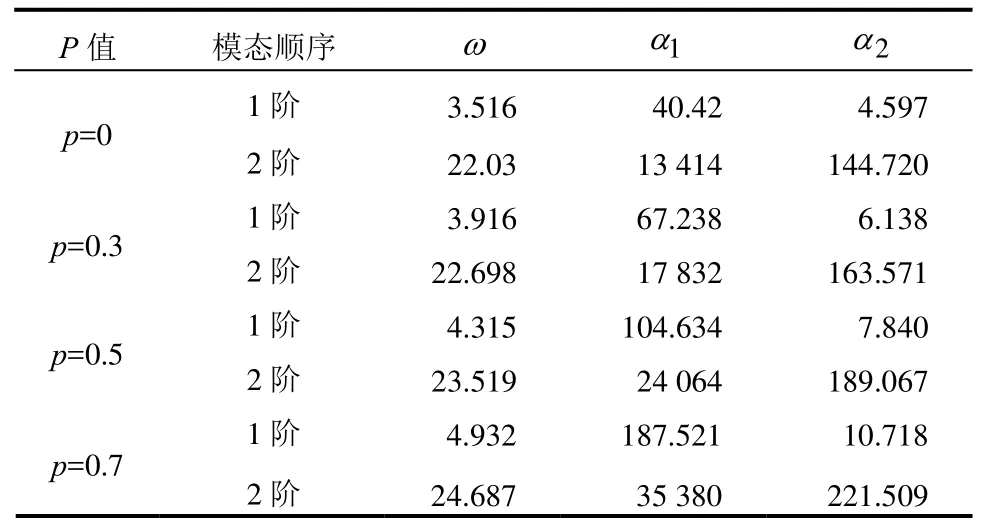
表2 前两阶模态的方程系数Table 2 The coefficients of first two modes

2 模态频率和振型函数的验证

为验证本文理论的正确性，采用东华动态信号测试系统(DH5927N)，利用锤击法进行了模态实验，分别选取p=0.3,0.5,0.7 三根变截面梁(铝合金)，并将其划分29等份，其中一端紧固在实验台上，另一端自由，将质量为1 g的加速度传感器(1A801E，灵敏度为2.488 mV/g)粘接在11号节点，如图3所示。

图3 模态锤击实验Fig.3 Model experiment setup

由于其质量非常小，不考虑它对振型及频率的影响。试件特性如表3和表4所示。

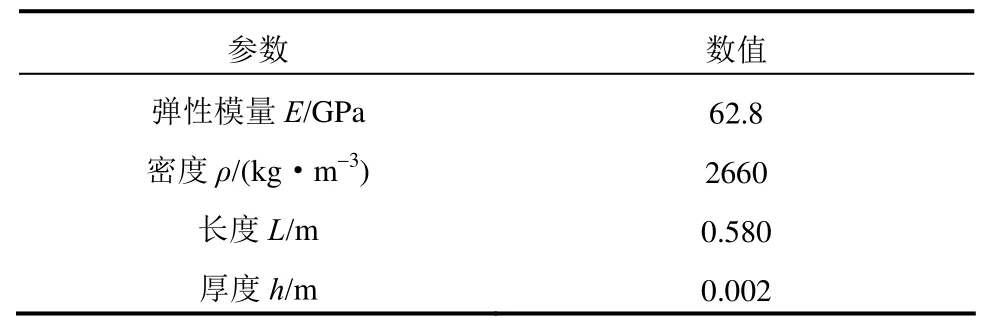
表3 悬臂梁的材料和几何特性Table 3 Material and geometric properties of the cantilever beams

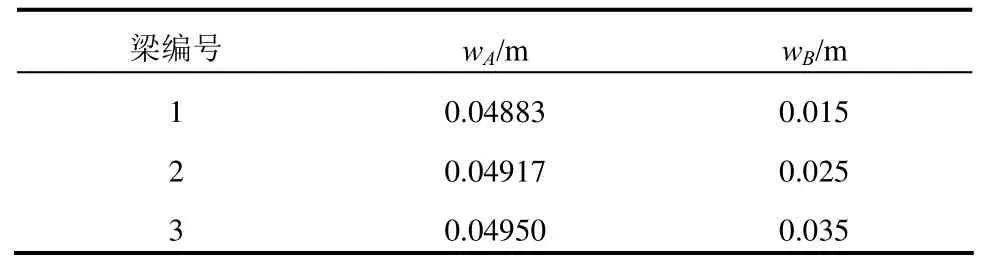
表4 悬臂梁的宽度Table 4 Width of the cantilever beams

实验时将测试系统采样频率设置为100 Hz，采用多点激励，单点拾振的方法，用力锤(型号为LC02 5 kN)依次敲击各点，同时观测力信号、加速度信号、频响函数、相干函数等指标来评价力锤敲击的有效性，如图4所示为锤击后的频响曲线图。由图4可知，该曲线为p=0.5的试件频响，在探测范围内，出现两个清晰的峰值，分别为一阶频率和二阶频率，其具体值如表5所示。

通过理论、有限元及实验的方法分别得到了p=0.3,0.5,0.7三根梁的固有频率。固有频率其中特征时间尺度为从表2中得到的无量纲频率ωi即可得到表5中实际试件的固有频率理论值。从表5中可以看出三种方法结论吻合较好，随着p的不断增大，梁的一阶和二阶固有频率也逐渐增大，理论结果与实验结果误差小于3%，充分说明本文表1中计算出的β有很好的精度。

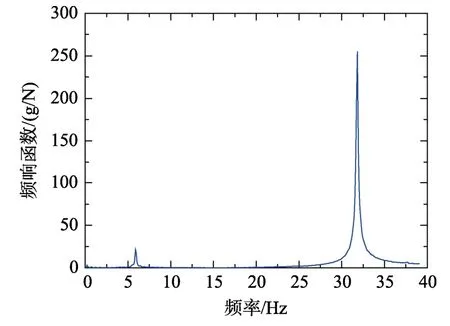
图4 实验测试频响函数Fig.4 Frequency response function of experiment test

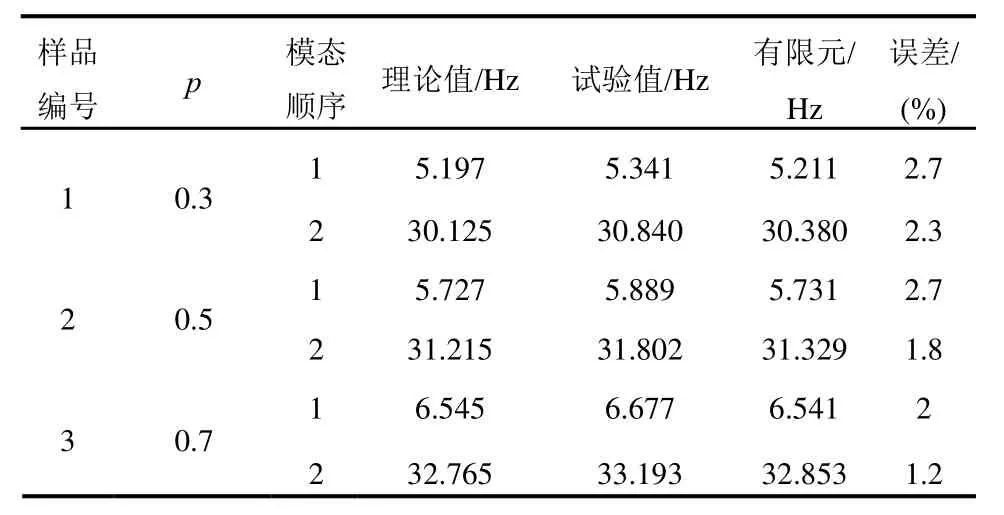
表5 试件的基频Table 5 The fundamental frequency of specimens

为了证实表1中计算出的C1、C2、C3、C4系数的正确性。笔者对比有限元模拟、有限元半解析法[16]及模态实验的振型结果。本文以p=0.5的梁为例，并将梁长与振幅均归一化，其中ymax为y方向位移最大值，得到了一阶和二阶振型图，如图5所示，其中实线加圆圈为有限元结果，实线加十字为实验结果，实线加三角形为有限元半解析解结果，实线加短横为理论结果，可以看出二阶振型四种方法均高度吻合；因一阶频率较低，实验时由于没有考虑传感器质量出现了误差，但整体趋势一致。

3 非线性幅频响应及实验验证

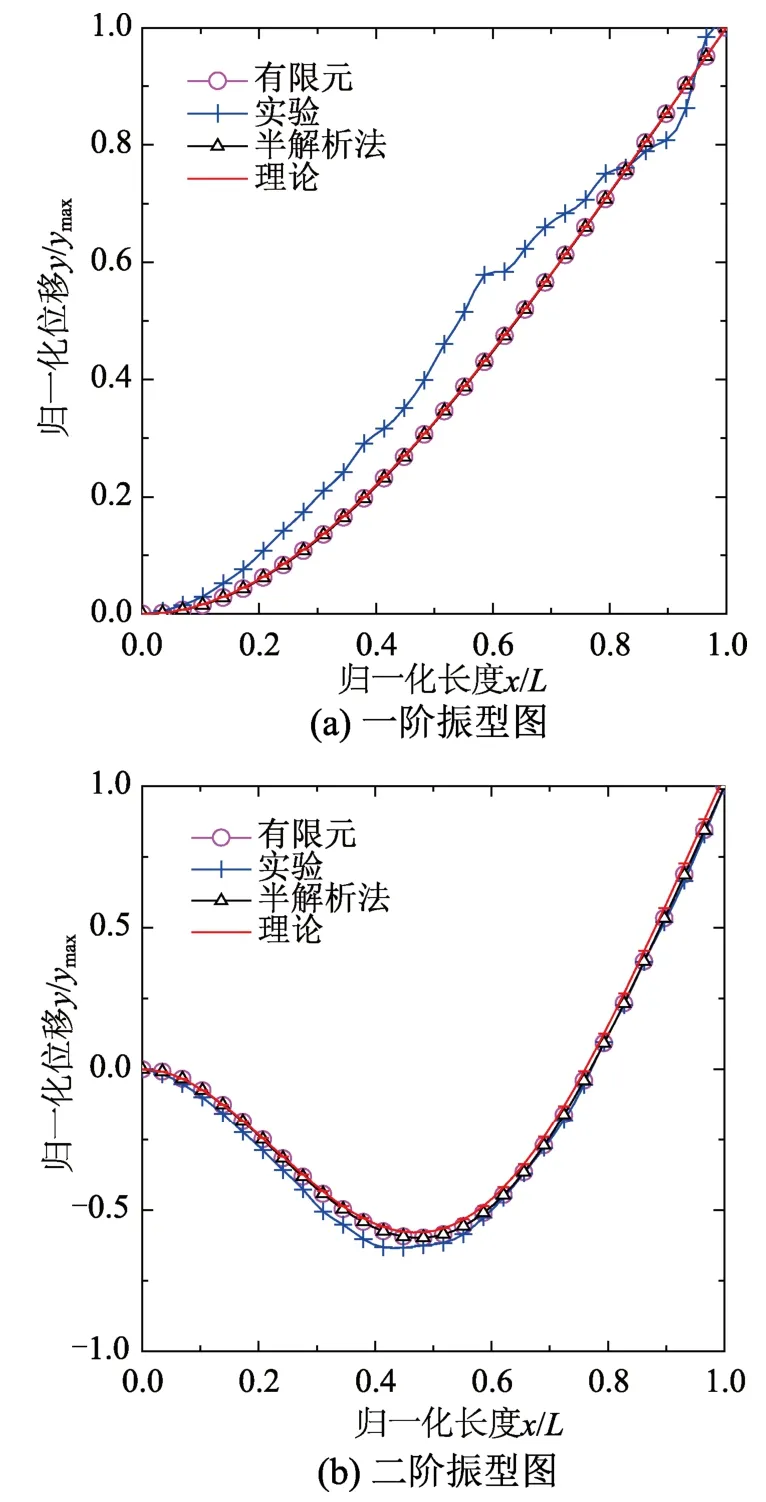
图5 p=0.5时四种方法得到的前二阶振型图Fig.5 Results for the first and second mode of the beam with p=0.5 using four methods

利用锤击法得到的频率仅为梁在小振幅、近似线性情况下的结果。下面将验证上述振型函数导出的弯曲非线性系数和惯性非线性系数的精确性。这两项系数在研究非线性振动时常用于多尺度法[15]。但是值得注意的是，基于摄动的多尺度法一般适用于弱非线性振动，其在处理大振幅的非线性时有其局限性，然而基于系统哈密尔顿函数能量平衡法，既可以适用于弱非线性也适用于强非线性。因此，本文采用能量平衡法(EBM)[17]来研究振动的幅频关系，其计算过程相比摄动法简单易操作而且精度较高。然后用得到的理论方法再次和大振幅的自由振动实验结果进行比较。

3.1 能量平衡法

式(22)的哈密尔顿能量为：

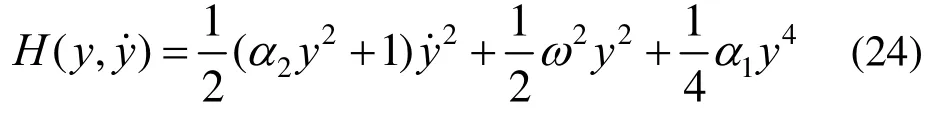
式中，第一项为动能，后两项为势能，假设式(24)的自由振动近似解的形式为：

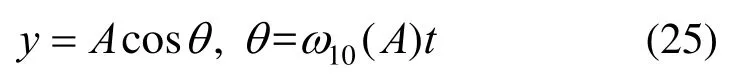
式中：ω10为待定的响应频率；A为振幅。将式(25)代入式(24)可得：

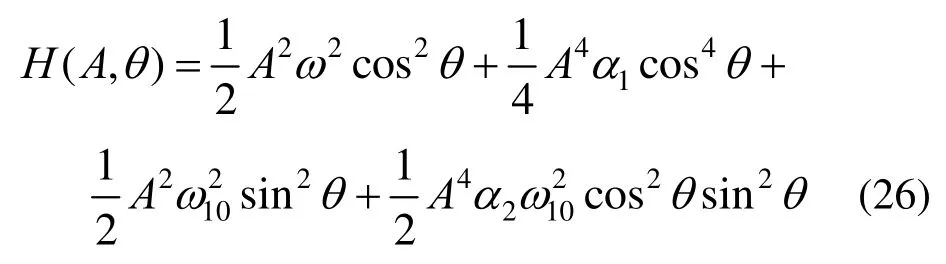
令θ=ω10t分别等于和0，可得两个情况下的哈密尔顿函数值：

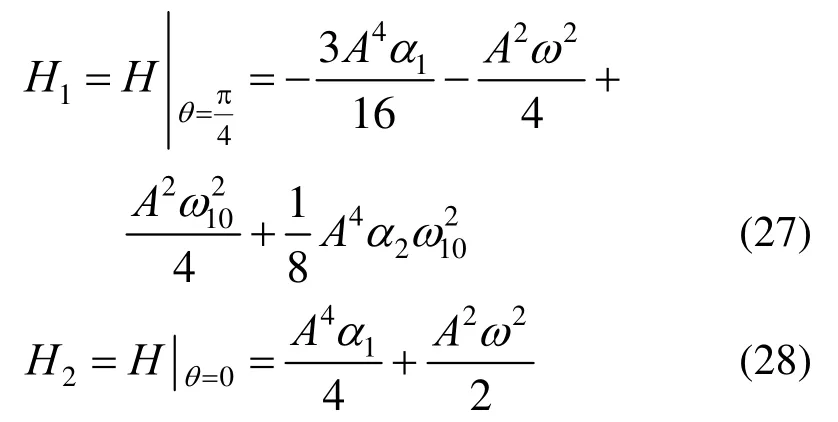
令这两个值H1、H2相等可解得：

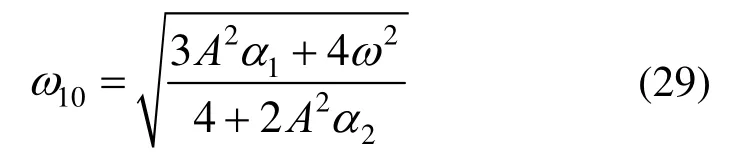
为了验证式(29)的值。需要将理论分析和实验结果对应起来。首先，选取距离梁根部为s0处的某一靶点M，利用基于超几何函数与Meijer-G函数的方法求得的振型函数，可以求得该点与自由端的振型函数值φ(s0)和φ(L)；随后，将梁一端固定，另一端偏离平衡位置δ/mm，可得M点的物理位移wmax(s0)，又w(s0,t)=q(t)φ(s0)=y(t)Lφ(s0)，所以w(s0,t)=Acos[ω10t]Lφ(s0)，则无量纲振 幅A和s0处的物理振幅wmax(s0)的关系为A=wmax(s0)/Lφ(s0)。分别将A、ω、a1、a2代入式(29)可以得到无量纲的频率ω10，由无量纲逆变换：f10=ω10/2πT，可以得到实际响应的频率。

考虑到实际情况中阻尼不可避免，在结果中添加了一个振幅衰减的阻尼因子η。则M点的横向位移随时间变化的函数可以表示为：

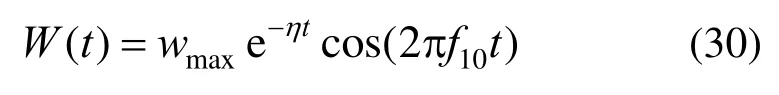
3.2 实验验证

如图6所示，选取一根变截面梁将其等分29份，并将左侧固定在实验装置上，然后用红外位移传感器(IL065)对准9号节点(距离固定端160 mm)，同时使传感器与梁之间的距离保持为80 mm并将其固定在有机玻璃槽内。以p=0.7的梁为例进行实验，实验时将自由端偏离平衡位置50 mm的位置，然后释放使其自由振动，通过红外传感器实时采集振动位移信号，将电压数据信号输入示波器内，即可得到实测的自由振动位移曲线时间历程图，如图7所示，虚线为理论计算得到的位移-时间历程图(式(30)中阻尼因子η取0.4)，实线为实测的自由振动位移-时间历程图(0 s～5 s)。

图6 变截面梁自由衰减振动实验Fig.6 Free decay vibration experiment of beam with variable section

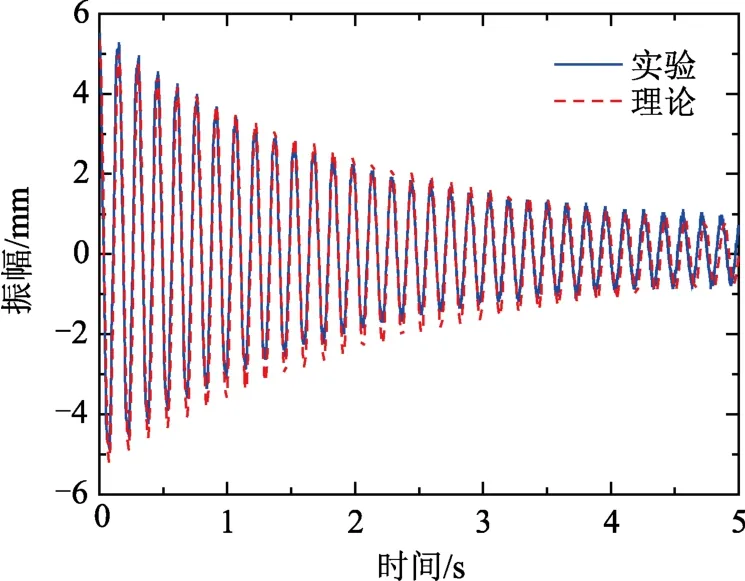
图7 p=0.7时的振动位移时间历程图Fig.7 Time history diagram of vibration displacement when p=0.7

从图7中可以清晰地看到本文理论计算的振型函数结合能量平衡法(EBM)中得到的位移-时间历程图的周期和与实验得到的曲线基本吻合，理论结果与实验在相位和振幅上存在微小的差别，误差产生的原因可能是理论上采用的阻尼比与实验中实际阻尼有偏差，该阻尼直接对响应的振幅和相位产生影响。本实验充分验证了能量平衡法中的非线性系数的正确性，从而也说明了本文振型函数的正确性和可靠性。

4 结论

(1) 本文提出了采用超几何函数和Meijer-G函数线性组合建立新的振型函数。通过理论计算得到的线性基频和模态振型与有限元法、有限元半解析法和实验锤击法得到的线性基频和模态振型进行了比较，验证了理论的正确性，该方法可为变截面梁振型函数求解提供指导。

(2) 采用能量平衡法求解强非线性振动，得到了振动幅频响应关系。此外，通过自由振动实验获得了变截面悬臂梁在大变形下的自由振动，发现实验获得的振动频率与能量平衡方法获得的频率非常一致，且实验检测的振动波形与理论预测吻合良好。验证了本文振型函数和非线性系数的正确性，为大变形的振动提供了有效依据。