基于有限质点法的含间隙铰平面机构动力分析

郑延丰，杨 超，刘 磊，罗尧治

(1.浙江大学空间结构研究中心，浙江，杭州 310058；2.浙江省空间结构重点实验室，浙江，杭州 310058；3.浙江绿城元和房地产开发有限公司，浙江，杭州 310058)

在常规的平面机构动力分析中，一般认为平面铰节点处于没有间隙的理想状态。但由于制造和安装误差，铰节点中不可避免地存在间隙。间隙的存在使得铰节点的轴承和轴颈易发生碰撞，从而使带间隙机构的动力响应与理想机构不同。近年来，学者们对间隙的力学模型和含间隙铰平面机构的动力行为开展了研究。弹簧-阻尼模型是经典的线性间隙接触力模型，但在接触瞬间和分离瞬间的接触力是不连续的[1]。Hertz[2]基于纯弹性理论提出了非线性的接触力模型，但没有考虑接触碰撞过程中的能量损失。Lankarani和 Nikravesh[3]提出了考虑弹性刚度项和阻尼项的接触法向力模型，可以考虑接触过程中的能量损失。Bai和Zhao[4]基于已有的间隙接触力模型提出了一种用于平面带间隙机构的混合接触力模型。Zhang等[5]研究了间隙铰节点对平面3-RRR机构动力行为的影响。在含间隙机构的动力问题中，若机构中含有多个间隙铰，则不同间隙铰之间的相互作用将使动力响应变得复杂[6]。若机构构件是柔性的，则在驱动力作用下构件将发生弯曲变形，从而改变间隙铰的动力行为[7]。

机构属于可变结构体系，其运动过程的模拟与常规结构存在较大差异。采用隐式求解的线性有限元方法在处理可变体系上存在困难，因为其集成的整体刚度矩阵是奇异的。非线性有限元法可用于机构问题求解，其中，几何精确方法(geometrically exact beam theory)[8]以转动参数为广义坐标，通过精确的几何非线性关系描述机构的变形，计算效率和计算精度高，但转动参数的更新和奇异性是该方法的难题。绝对节点坐标法(absolute nodal coordinate formulation, ANCF)[9]采用位移场的斜率矢量避免复杂的转角问题，建模直观，但自由度多，计算效率低下，同时收敛性也存在问题。多体系统动力学可用于模拟带间隙机构的动力响应[10－12]，但随着间隙节点数量的增加，约束多体系统逐渐变为无约束或节点-力系统[13]；并且由于间隙节点之间的相互作用，其动力行为变得更加复杂。

有限质点法(finite particle method, FPM)是基于向量式有限元发展的、面向结构行为的分析方法，已应用于动力、几何非线性、材料非线性、屈曲/褶皱失效、机构运动、接触碰撞、断裂等结构复杂行为分析[14]。在有限质点法中，采用显式求解方案，不需集成整体刚度矩阵，因此可避免刚度矩阵奇异，用于机构运动分析时不会存在困难[15]。有限质点法将结构离散为质点，以质点代表结构的运动，间隙碰撞产生的接触力可直接作用于质点，不需要对刚度矩阵进行修正。因此基于有限质点法引入含间隙铰的分析方法在原理上是可行的，在处理上也十分方便，可为更精细的机构运动模拟提供手段。

本文基于有限质点法，对含间隙铰的平面机构开展动力分析。首先给出有限质点法平面机构分析的原理，包括质点运动控制方程和平面梁单元的内力计算公式。然后引入Lankarani-Nikravesh模型和修正库仑摩擦模型，来计算间隙铰中轴承和轴颈碰撞过程中的接触力和摩擦力。最后以几个典型的平面机构为例开展动力分析，研究间隙铰对机构动力响应的影响。本文的创新点包括以下两个方面：1)将有限质点法用于求解含间隙机构动力问题，拓展了有限质点法的应用领域，也为这类问题的求解提供一种有效手段；2) 该方法建模直观，编程简单方便，不仅可求解单间隙铰、刚性机构的动力问题，还可用于多间隙铰、柔性机构问题的动力分析。

1 有限质点法平面机构分析原理

在有限质点法中，平面机构被离散成质点，代表机构的位置、质量、受力、变形和边界条件，即点值描述。机构杆件被离散为平面梁单元，但单元的概念和作用被弱化，仅用于表示质点之间的相互作用关系。在时间域上，质点受力后的运动轨迹被划分成许多离散的微段，并通过一组时间点上的值来描述各个质点的位移，即途径单元描述。

1.1 质点运动控制方程

离散模型中所有质点的运动都遵循牛顿第二定律。对于平面梁单元连接的质点，其运动变量可分解为沿平面坐标轴方向的2个线位移和1个角位移，分别对应坐标轴方向的2个力和1个弯矩，如图1所示。

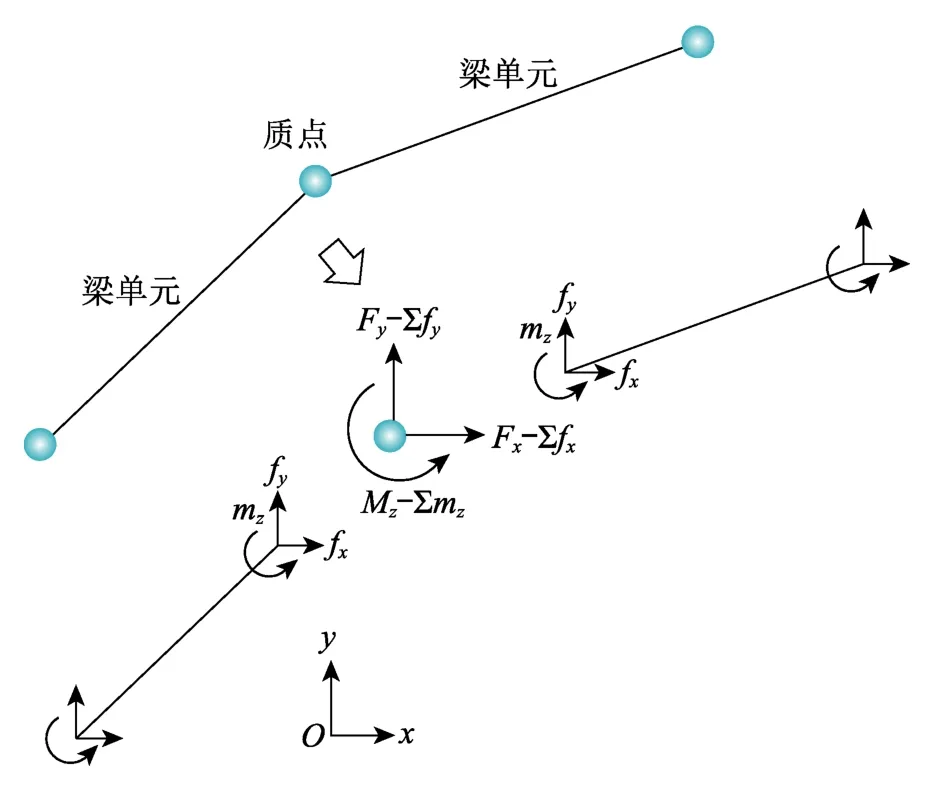
图1 平面机构的质点受力Fig.1 Particle force of planar mechanisms

平面机构的质点运动方程可具体表达为：

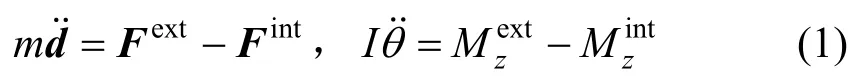
式中：m为质点的质量；d=[dx,dy]T为质点线位移向量；Fext=[Fx,Fy]T为质点外力向量；Fint=为梁单元传递至质点的内力向量；I为质点的质量惯性矩；θ为质点角位移；为质点外力矩；为各个梁单元传递至质点的内力矩。质点的质量m和质量惯性矩I可通过下式集成：

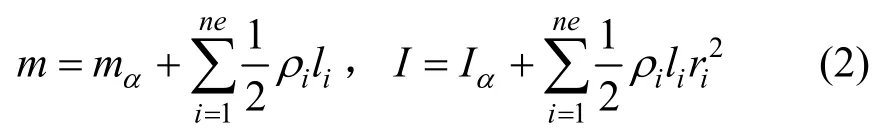
式中：mα和Iα分别为质点α的集中质量和集中质量惯性矩；ne为与质点相连的梁单元数量，对第i个梁单元；iρ为其线密度；li为长度；ri为截面回转半径。

有限质点法采用显式积分方案，可由中心差分法估算质点的加速度和角加速度：

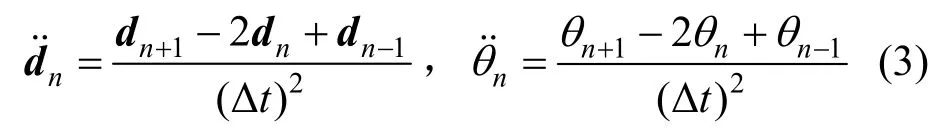
式中，Δt为时间积分步长。将式(3)代入式(1)，可由n-1和n时刻位移得到n+1时刻位移，同理可得n+1时刻角位移，如式(4)所示。迭代求解，可得结构在外荷载下的位移反应。

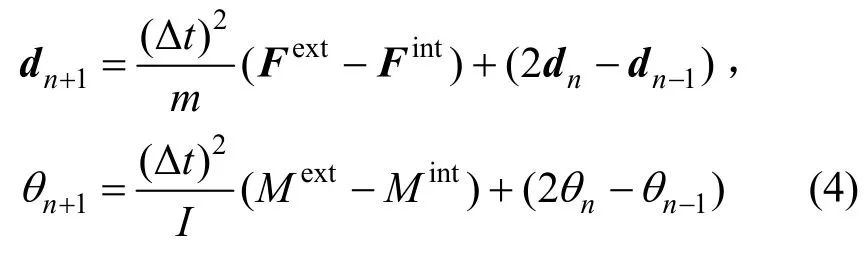
为使计算收敛，计算步长需要小于临界时间步长。本文采用的平面梁单元临界时间步长Δtmin可按下式估算[16]：

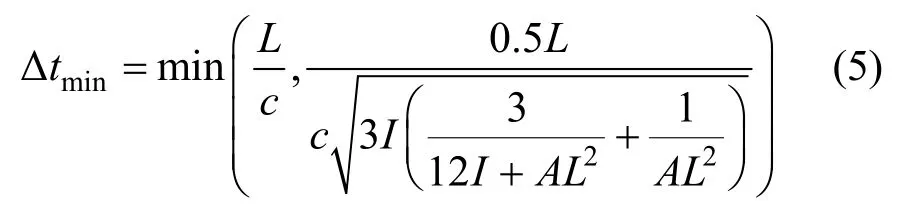
式中：L为梁单元长度；为波速；E为弹性模量；L、A和I分别为梁单元的长度、截面积和截面惯性矩。由于间隙处存在接触非线性行为，因此本文建议将Δtmin乘以小于1的系数tα(建议取0.5左右)，以保证计算收敛。

1.2 平面梁单元内力

喻莹[17]推导了有限质点法三维梁单元的内力计算公式。退化到二维，可得到平面梁单元的内力计算公式[15]。设梁单元AB在ta和tb( =ta+ Δt)时刻的平面位置分别为节点转角分别为则单元从ta到tb时刻的位移和转角分别为：

ta和tb时刻单元主轴方向向量分别为：

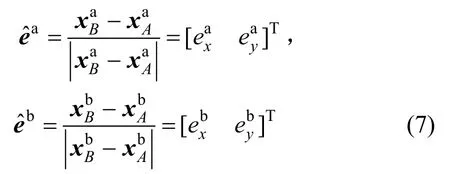
则两轴之间的转动角度为：

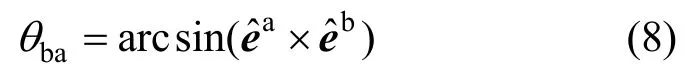
单元位置从ta时刻的AB运动到tb时刻的A′′B′。为计算单元纯变形，将单元进行逆向运动，如图 2所示。逆向平移量为-ΔxA，逆向转动角度为-θba。由于单元变形后仍为直线，虚拟位置A′′B′′与AB共线。在单元的虚拟位置，得到单元的纯变形为：

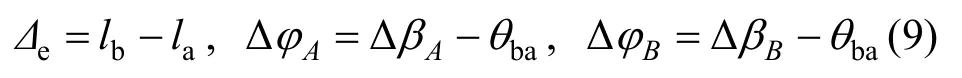
式中，l为梁单元的长度。

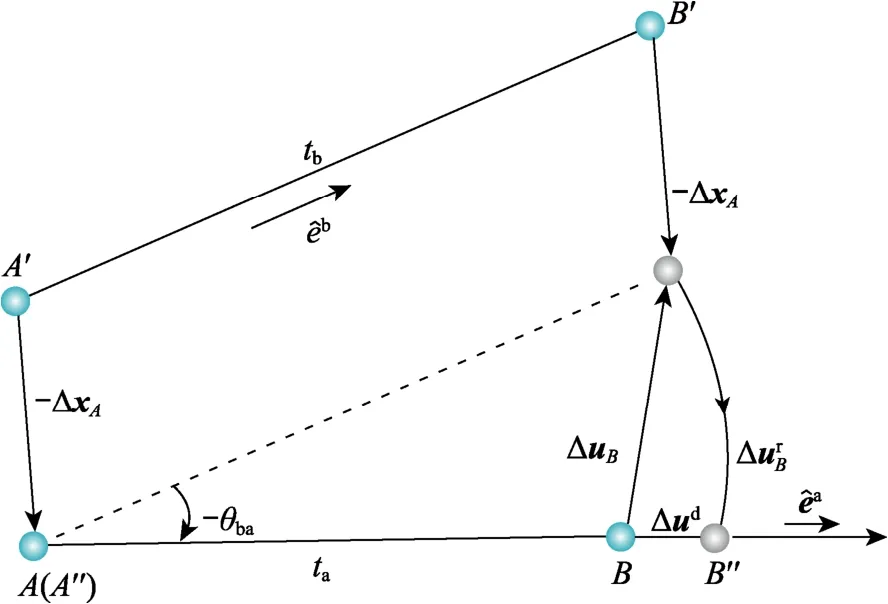
图2 平面梁单元的虚拟逆向运动Fig.2 Fictitious reversed rigid-body motion of planar beam element

局部坐标系下，单元在途径单元的内力增量为：

式中，Iz为截面转动模量。将单元内力增量叠加到ta时刻参考构型的内力全量上，转换至整体坐标系，再将单元经过正向平移ΔxA和正向转动θba，可得到平面梁单元tb时刻的单元内力。平面内的平移和转动对单元弯矩的方向和大小没有影响，因此不需对单元弯矩进行处理。单元内力tb时刻的内力为：

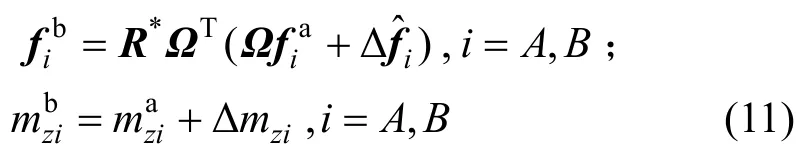
式中：Ω为单元局部坐标系和整体坐标系的转换矩阵；R*为旋转矩阵，如下式所示：

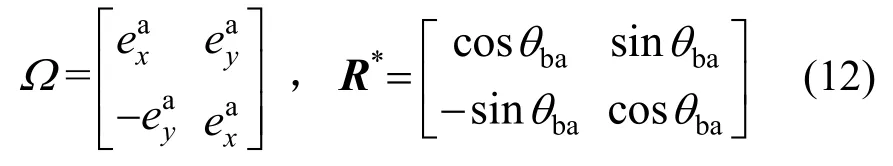
2 平面转动铰模型

2.1 理想转动铰模型

在平面机构中，转动铰是由轴承和轴颈构成的。理想转动铰中轴承和轴颈的相互作用力可通过运动约束条件推导得到，如图3(a)所示。设轴承和轴颈的中心点分别为B和J，其运动控制方程为：

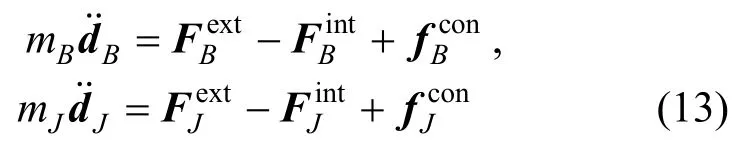
将式(14)代入式(13)得：

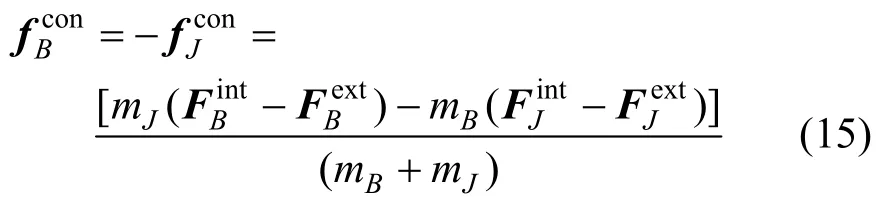
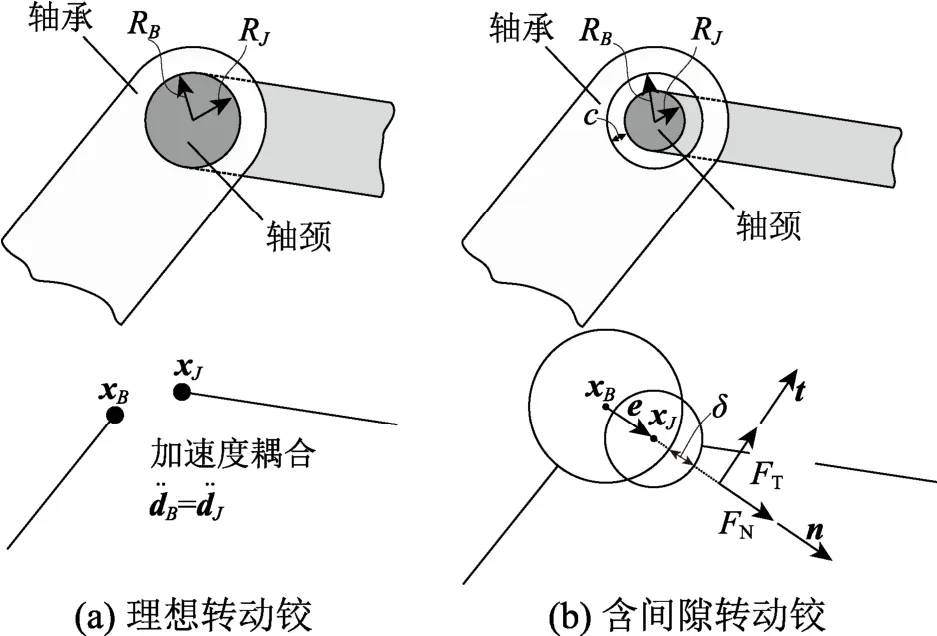
图3 理想转动铰和含间隙转动铰的力学模型Fig.3 Mechanical model of ideal revolute joint and revolute joint with clearance

2.2 含间隙转动铰模型

含间隙的转动铰中轴承与轴颈的相互作用力可根据轴承和轴颈的接触情况推导得到。

2.2.1 接触侦测

对含间隙的转动铰(图3(b))，虽然轴颈的运动受到轴承的约束，但有一定的自由运动空间。轴颈在轴承中有自由运动、碰撞、接触三种不同的运动状态。在自由运动状态中，轴颈在轴承的内圈边界内自由运动，轴颈与轴承间无接触和相互作用力。碰撞状态是一个临界状态，出现时间极短，发生在自由运动结束时，碰撞力作用在转动铰中且很快消失，该状态的运动和动力特性是离散的，两个碰撞体之间发生有效的动量转化。碰撞结束后，轴颈可能进入接触或者自由运动状态。在接触状态，轴颈与轴承始终保持接触且相互之间做滑行运动，侵入深度随轴颈运动而不断变化；这种状态随着轴颈与轴承的分离而终止，后续轴颈进入自由运动状态。

接触状态可通过间隙大小及轴承、轴颈的相对位置判断。如图3(b)所示，转动铰的间隙大小为：

式中：RB和RJ分别为轴承的内半径和轴颈的外半径；OB和OJ分别为轴承和轴颈的中心，坐标分别为xB和xJ。则连接轴承和轴颈中心的偏心向量e可以表示为：

轴颈与轴承相互碰撞导致的侵入深度δ可表示为：

轴颈与轴承碰撞平面的法向单位向量n和偏心距向量在同一条直线上。为计算接触力和摩擦力，在接触点处建立局部坐标系(n,t)：

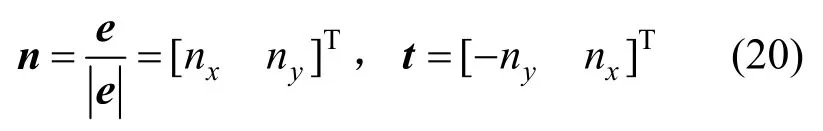
2.2.2 法向接触力

本文采用Lankarani-Nikravesh模型[3]计算间隙产生的法向接触力。Lankarani和Nikravesh[3]基于Hertz接触理论，提出了非线性的弹簧阻尼模型。该模型将法向接触力表示为侵入深度的函数，并考虑了接触点的局部变形及接触过程的持续时间；同时引入与回弹系数、侵入速度相关的粘滞阻尼项来反映材料阻尼导致的能量损失，可考虑碰撞体材料的属性、局部变形、碰撞速度等因素的影响。因此国内外的学者广泛地应用该模型对含间隙机构动力学进行分析研究。

Lankarani-Nikravesh模型的接触力公式为：

式中：ce为恢复系数；νk为泊松比；Ek为弹性模量；为初始碰撞时刻碰撞点的相对运动速度；为接触过程中的瞬时侵入速度；n为非线性系数，一般可取1.5。

2.2.3 切向摩擦力

本文采用修正库仑摩擦模型[18]来计算切向摩擦力。为简便起见，假设轴承和轴颈间的摩擦为滑动摩擦。滑动摩擦力大小可由下式计算：

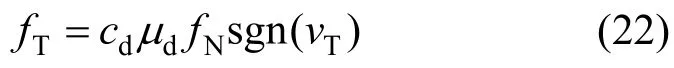
式中：μd为动摩擦系数；sgn(⋅)为符号函数；cd为修正系数：

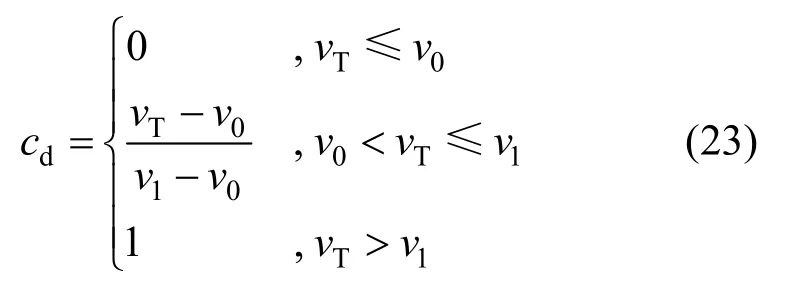
式中：v0和v1为临界系数，可按经验取值；vT为轴颈和轴承在接触点的相对切向速度。修正系数cd可避免当vT接近零值时摩擦力的突然变向。

vT可按以下方法计算：轴承和轴颈在接触点Q处的坐标可表示为：

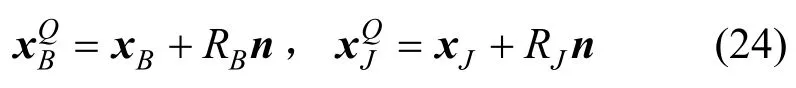
将其对时间求导，可得对应的速度：

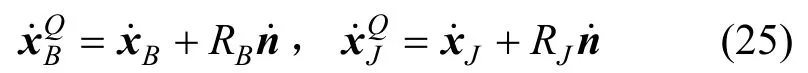
则相对切向速度vT和法向速度vN可以通过投影得到：

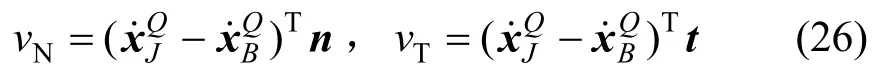
2.2.4 接触力集成

计算出轴颈和轴承之间的法向接触力和切向摩擦力后，轴颈和轴承对应质点所受总的接触力可表示为：

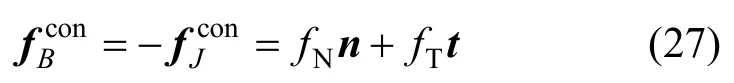
式中，fN和fT分别为法向接触力和切向摩擦力。法向接触力通过轴承和轴颈的中心，不会产生附加力矩。但摩擦力是沿接触点切向的，会对轴颈或轴承中心产生附加力矩。附加力矩大小为：

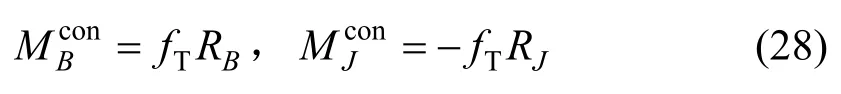
轴颈和轴承对应质点的运动控制方程可写为：

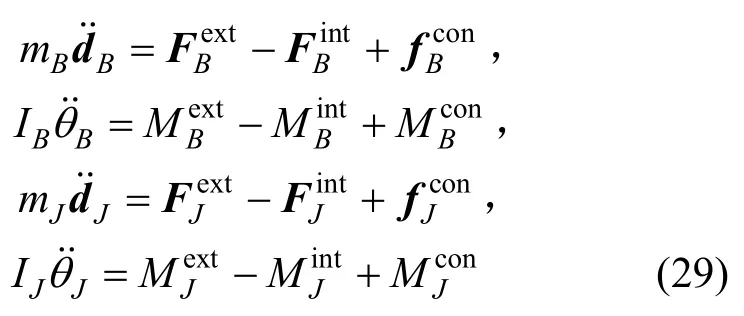
以上运动控制方程的求解与一般质点类似。

2.3 计算流程

通过对轴颈和轴承的接触侦测、接触力和摩擦力计算、接触力集成，即可求解各质点位移，进入下一时刻，更新平面梁单元内力，计算质点合力，从而迭代求解出结构运动过程中各时刻的位移。完整的计算流程如图4所示，其中的突出标识为在原算法基础上增加的考虑间隙接触的计算步骤。

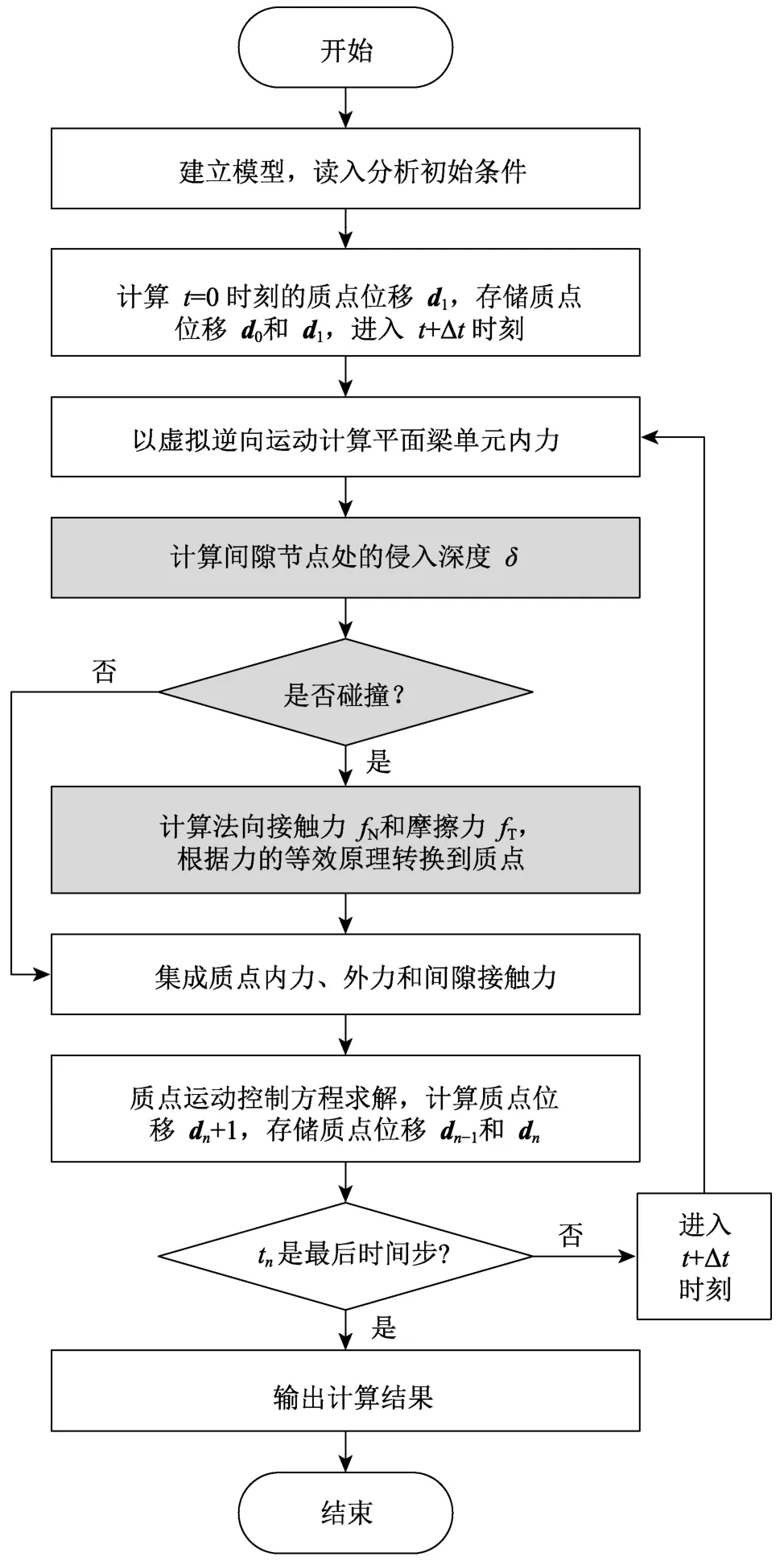
图4 含间隙铰平面机构的有限质点法计算流程Fig.4 Flowchart of finite particle method for planar mechanism with clearance revolute joint

3 数值算例

从上述分析和推导过程中可以看出，这种间隙铰计算方法在已有的算法框架基础上实现了间隙处的接触侦测、接触力计算和集成。本节通过算例验证这种间隙铰计算方法在平面机构动力分析中的有效性和稳定性。

3.1 平面四杆机构

本文首先对一个含间隙转动铰的平面四杆机构进行模拟。如图5所示，此机构包含驱动杆、连杆和随动杆，整个机构包括3个理想转动铰，分别连接驱动杆与支座、驱动杆与连杆、随动杆与支座，而随动杆与连杆之间为含间隙转动铰。机构各构件的特性见表1，间隙铰的模拟参数见表2。构件截面尺寸选取方式如下：设构件的密度为ρ，质量为m，长度为l，质量惯性矩为I，则构件截面面积A=m/(ρl)，截面惯性矩为Iz=(I/ρl)，因此满足截面面积A和截面惯性矩Iz的截面均可选为算例尺寸。本算例构件选用矩形截面，宽和高见表1。

图5 含间隙铰的平面四杆机构Fig.5 Planar four-bar mechanism with clearance joint

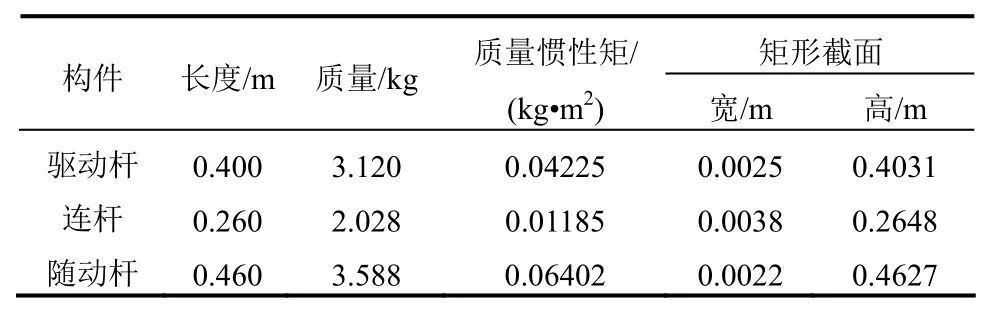
表1 四杆机构各构件的特性Table 1 Properties of each component in four-bar mechanism

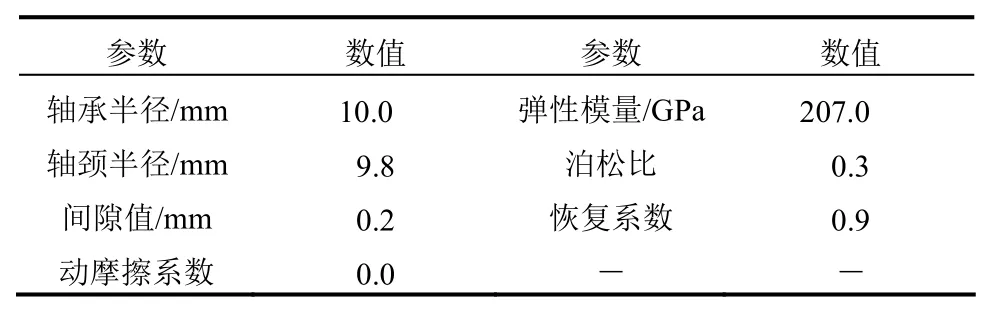
表2 四杆机构中间隙铰的模拟参数Table 2 Simulation parameters for clearance joint in four-bar mechanism

采用有限质点法，将该机构各构件分别离散为5个质点和4个平面梁单元。为模拟刚性构件，梁单元的弹性模量可取相对较大的值。理想铰处两个质点之间的作用力通过上述位移耦合模型进行计算，间隙铰处两个质点的作用力通过上述间隙接触模型进行计算。在初始状态，驱动杆与地面垂直，初始角位移与角速度均为零。在驱动杆支座端施加逆时针强迫角位移以模拟驱动力，稳定后的角速度为50 π rad/s。为减小突加荷载引起的振动，首先进行0.12 s的线性加载，使驱动杆的速度从0线性增加至50 π rad/s。之后的计算总时间为0.14 s，积分时间步长为10-7s。

为考察间隙对机构动力响应的影响，本文首先对全为理想铰节点的平面四杆机构进行分析，然后将连杆和随动杆之间的铰节点改为间隙铰节点进行分析。图6(a)和图6(b)分别绘制了一个运动周期内(驱动杆角度为0°～360°)随动杆的角速度和角加速度的时程曲线。从图中可以发现，间隙的存在对随动杆角速度的影响不大，但对其角加速度有较大影响。在角速度达到峰值的时刻附近，含间隙铰的机构角速度有一定的波动，对应的角加速度曲线剧烈振荡，其最大值相对于理想铰机构有较大增加。图6(c)绘制了间隙铰处的接触力，可以发现当驱动杆角度为250°～270°时，间隙铰的接触力剧烈震荡。为考察间隙铰对动力效应的影响，分别定义随动杆角加速度和间隙接触力的放大系数DEα和DEF：

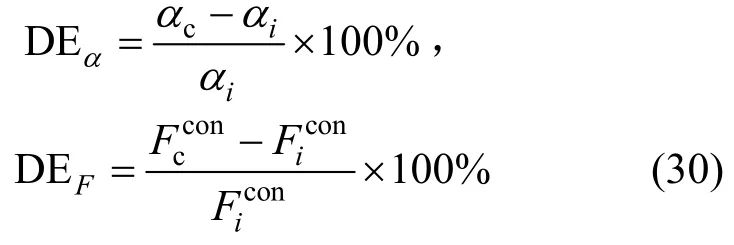
式中：αi和αc分别为理想铰机构和含间隙铰机构中随动杆的最大角加速度；分别为理想铰机构和含间隙铰机构中接触力最大值。从图6(b)和图6(c)分别提取角加速度和接触力的最大值，可以得到DEα和DEF分别为66.9%和16.6%。从图6(c)可以看出，在驱动杆角度为0°～225°时，理想铰接触力振动略大于间隙铰接触力，其原因为：驱动杆作用力通过平面梁单元传递给质点，而梁单元内力也存在一定程度的振动；本文方法中的质点运动方程采用牛顿第二定律求解，质点在梁单元内力作用下也表现为围绕平衡点进行一定幅度的振动，但其振动不影响计算结果的收敛性。理想铰机构中，没有耗能的阻尼项，从而振动没有被消除；含间隙铰机构中，接触力中的耗能阻尼项减小了接触力的振动，从而接触力曲线较平滑。

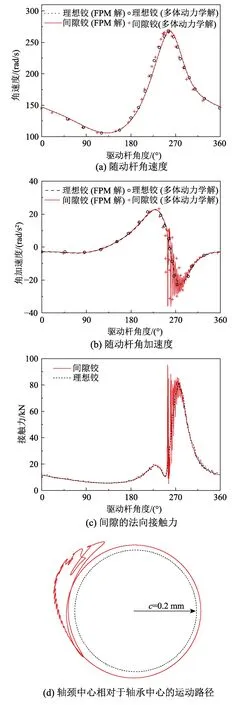
图6 含间隙铰的平面四杆机构模拟结果Fig.6 Simulation results for planar four-bar mechanism with clearance joint

通过跟踪机构运动的全过程可知，在运动初期，轴颈和轴承出现分离现象，随后轴颈与轴承始终保持接触状态。图6(d)绘制了稳定周期运动下轴颈中心相对于轴承中心的运动路径，可以看出侵入深度δ＞0，说明轴颈和轴承保持接触状态。δ在一个周期运动中的某段时间内增大，表明对应的法向接触力达到峰值。以上分析结果与文献[19]中采用多体动力学方法分析的结果一致，证明了有限质点法用于处理间隙转动铰的正确性。

3.2 曲柄滑块机构

为验证本文方法在柔性机构及含多个间隙铰机构的动力问题求解方面的适用性，采用本文方法对一含间隙铰的曲柄滑块柔性机构进行动力模拟。

如图7所示，此机构包含驱动杆、连杆和滑块，滑块可在水平方向自由滑动。整个机构包括两个理想转动铰，分别连接驱动杆与支座(铰1)、驱动杆与连杆(铰2)，连杆与滑块之间为含间隙转动铰(铰3)。柔性连杆在驱动力作用下将发生弯曲变形。机构各构件的特性见表3，间隙铰的模拟参数见表4。

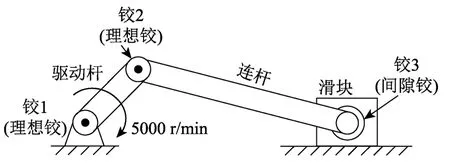
图7 含间隙铰的曲柄滑块机构Fig.7 Slider-crank mechanism with clearance joint

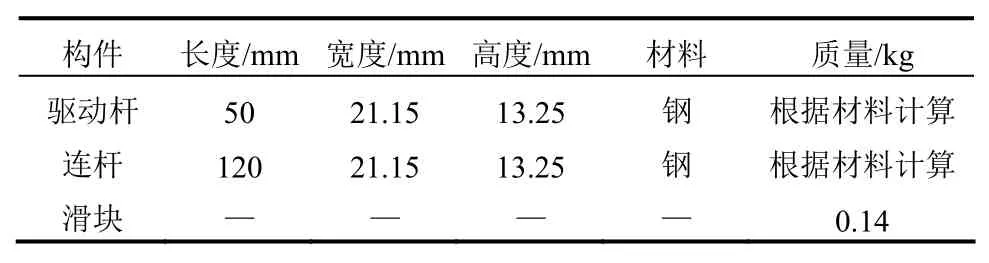
表3 曲柄滑块机构各构件的特性Table 3 Properties of each component in slider-crank mechanism

表4 曲柄滑块中间隙铰的模拟参数Table 4 Simulation parameters for clearance joint in slider-crank mechanism

采用有限质点法，将驱动杆离散为2个质点和1个平面梁单元，将连杆离散为5个质点和4个平面梁单元。滑块以独立质点模拟，其质量通过质点的集中质量形式施加，并约束该质点的竖向线位移和角位移，以模拟滑块的约束条件。理想铰和间隙铰的模拟方法与平面四杆机构的算例相同。在初始状态，驱动杆与地面平行，初始角位移与角速度均为零。在驱动杆支座端施加顺时针强迫角位移以模拟驱动力，稳定后的角速度为5000 r/min。为减小突加荷载引起的振动，首先进行0.024 s的线性加载，使驱动杆的速度从0线性增加至5000 r/min。之后的计算总时间为0.096 s。考虑机构中连杆分别为刚性和柔性两种情况，其弹性模量分别取2.07×1013Pa和2.07×1011Pa 。根据式(5)，积分时间步长分别取为1.59×10-7s和4.2×10-7s。

图8(a)～图8(b)对比了理想刚性机构、含间隙铰刚性机构和含间隙铰柔性机构的动力响应，并分别绘制了两个运动周期内(驱动杆角度为0°～720°)滑块的速度和加速度的时程曲线。可以看出，含间隙铰刚性和柔性机构的动力响应振动幅度和峰值均比理想刚性机构的动力响应大。相对于含间隙铰刚性机构，含间隙铰柔性机构的速度和加速度振动幅度要小一些。从图8(c)可以看出，含间隙柔性机构的接触力峰值也比含间隙刚性机构要小约40%。以上结论与文献[20]的试验结果相符。图8(d)还绘制了间隙铰中轴颈中心相对于轴承中心的运动路径，可以看出运动过程均经历了自由运动、碰撞和接触三种状态，但柔性机构中轴颈的相对运动路径更不平滑。从图示结果可以看出，本文方法和文献[7]通过理论推导和分析得到的结果一致，验证了本文方法在求解含间隙柔性机构动力问题的适用性。

为进一步验证本文方法在求解多间隙铰机构动力问题的有效性，将本算例中驱动杆和连杆之间的转动铰(铰2)也设为含间隙铰，比较理想铰、单个间隙铰和多个间隙铰柔性机构的动力效应。图9(a)～图9(c)绘制了多个间隙铰机构的滑块速度、加速度以及间隙接触力的时程曲线。相比单个间隙铰，多个间隙铰机构中滑块速度的峰值有所增大，同时峰值处相位滞后更为明显；同时，多间隙铰机构中加速度和接触力峰值均有较大幅度增加。以上结果说明多个间隙铰将显著增加机构的动力响应。图9(d)绘制了轴颈中心相对于轴承中心的运动路径，相对于单间隙铰机构，多间隙铰机构中的铰3自由运动状态的幅度和范围更大，而铰2主要以接触状态为主。

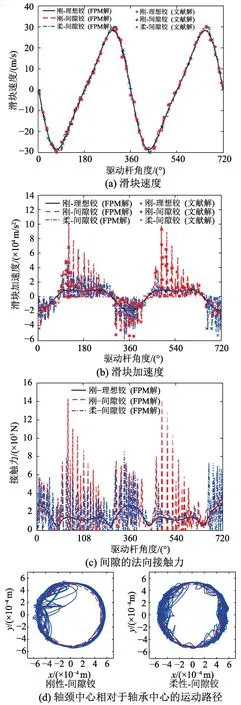
图8 含单个间隙铰的曲柄滑块机构模拟结果Fig.8 Simulation results for slider-crank mechanism with single clearance joint

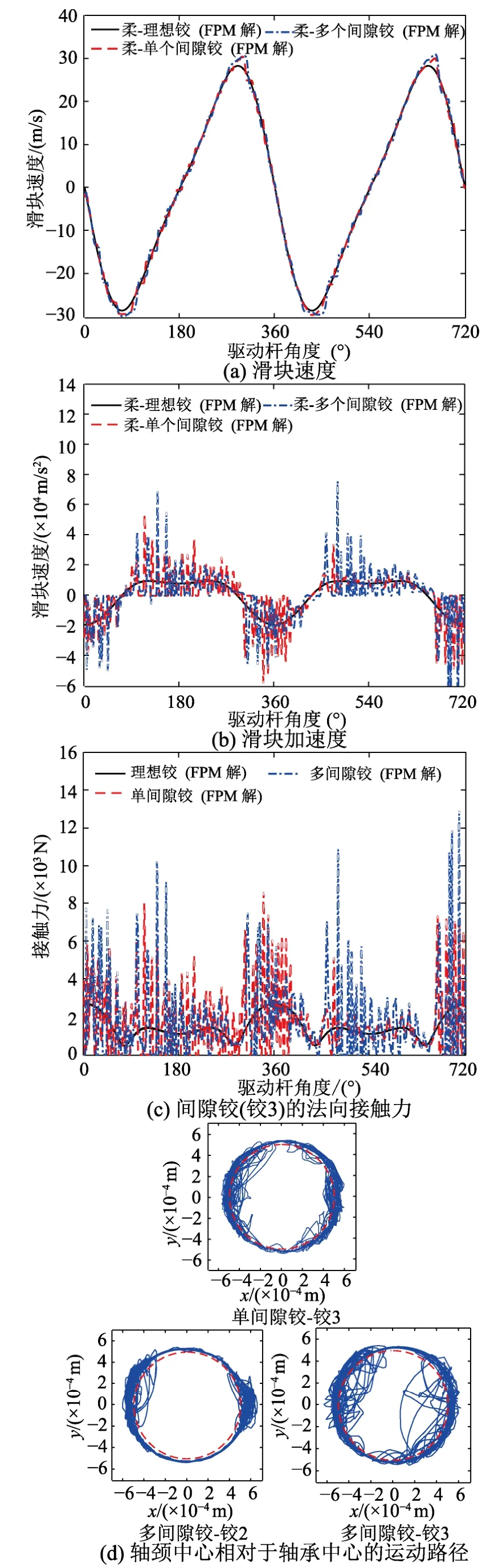
图9 含多个间隙铰的曲柄滑块机构模拟结果Fig.9 Simulation results for slider-crank mechanism with multiple clearance joints

从本算例可以看出，本文方法不需进行复杂的理论推导，适合用于建立各种复杂机构模型；在进行刚性和柔性机构分析时，只需调整构件的弹性模量即可；同时适用于多间隙铰机构动力分析，编程简单方便，适用性强。

4 结论

有限质点法不需要集成整体刚度矩阵，适合进行机构动力分析，质点间作用力的处理也十分方便。本文基于有限质点法，建立了含间隙铰平面机构的动力分析方法，算例表明本文方法是正确并有效的，建模直观，编程简单方便，并且适用于求解含多个间隙铰的柔性机构动力问题。值得说明的是，其他的接触力和摩擦力模型在本文提出的计算框架下实现起来也非常容易。利用本文方法对平面四杆机构和曲柄滑块机构进行了动力分析，结果表明间隙铰对机构运动的位移和速度影响不大，但会使机构的加速度和间隙铰的接触力有较大振荡。利用本文提出的间隙铰分析方法，可在实际工程中考虑间隙对复杂机构或含机构运动的结构进行分析，从而评估间隙产生的动力效应，为机构或结构设计提供指导。