高延性混凝土面层加固受弯无筋砌体墙抗震性能试验研究

2020-03-16邓明科董志芳樊鑫淼梁兴文

工程力学 2020年3期

邓明科，董志芳，樊鑫淼,2，梁兴文

(1.西安建筑科技大学土木工程学院，陕西，西安 710055；2.中机国际工程设计研究院有限责任公司，湖南，长沙 410007)

砌体结构是我国建筑结构的主要形式之一。汶川地震的震害调查表明[1－2]，砖砌体墙发生脆性剪切破坏时，结构损坏严重、修复困难，通常拆除重建；砖砌体墙发生正截面弯曲破坏时，墙体变形较大，损坏相对较轻，容易修复。国外对砌体墙平面内的弯曲破坏进行研究[3]，提出了钢筋网水泥砂浆面层、粘贴纤维复合材、加筋喷射混凝土层等抗震加固方法。上述方法均可在一定程度上提高砌体墙的抗震承载力[4－5]，但由于材料本身的脆性，加固层易剥离或脱落，而且也存在施工复杂、对原结构扰动大、工期长、造价高等缺陷。因此，采取高效经济的加固方式对提高受弯砌体墙的抗震性能具有重要意义。

高延性水泥基复合材料[6](engineered cementitious composites，ECC)是美国Li教授依据微观力学和断裂力学原理配制出的高性能水泥基复合材料，具有良好的拉伸和剪切变形能力[7－8]。日本和欧美等已将其应用于高层建筑、道路、大坝、车站的加固修复工程[9]。Dehghani等[10]开展了ECC加固砌体墙的对角受压试验研究，结果表明ECC加固技术能有效提高砌体墙的抗剪承载力。Singh等[11]研究了采用预制ECC板加固砌体梁受拉侧的加固效率。张远淼等[12]将ECC用于修复震损剪力墙，结果表明ECC加固试件的承载力得到恢复。本课题组采用ECC设计理论配制了高延性混凝土(high ductility concrete，简称HDC)，已将其应用于加固砌体墙[13－15]、钢筋混凝土柱的底部塑性区[16－18]和连梁等[19]构件中，均取得了良好的效果。

为解决传统加固材料的脆性特征和施工复杂、对原结构扰动大、工期长、造价高的问题，本文提出采用HDC面层对受弯无筋砌体墙进行抗震加固。通过对5片砖墙的拟静力试验，研究HDC面层加固受弯无筋砌体墙的破坏机理和抗震性能，然后通过统计分析得到HDC加固砌体基于位移角的易损性曲线，为HDC加固受弯砌体抗震性能设计和性能指标的量化提供依据。

1 试验概况

1.1 试件设计

试验共设计了5片受弯无筋砌体墙，其中试件HDC-W3带有构造柱，其他试件均为无构造柱砖墙；墙体厚240 mm，高宽比均为1.2，构造柱截面尺寸为240 mm×240 mm，纵筋为箍筋为试件详细尺寸如图1所示。试验中对4片墙体进行加固，试件W2的绑扎钢筋网规格尺寸为6@300，并采用6@600的S形穿墙筋拉结；试件HDC-W1两侧分别采用15 mm厚HDC面层和20 mm厚水泥砂浆面层加固，试件HDC-W2和HDC-W3均采用15 mm厚HDC面层双面加固；HDC面层均为人工抹面。试件的加固方案详见表1。

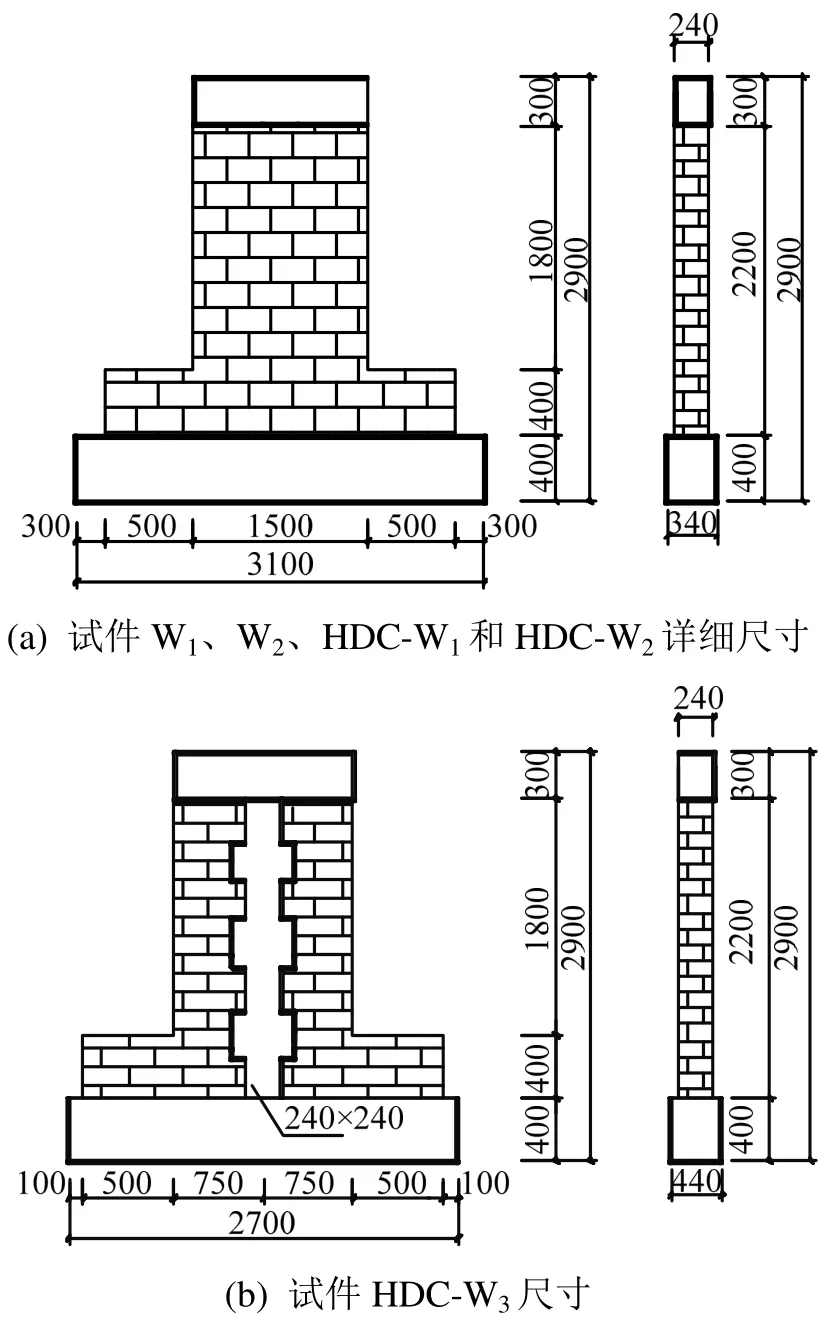
图1 试件详细尺寸Fig.1 Details of specimens

表1 试件加固方案Table 1 Strengthening scheme of specimens

1.2 材料参数

本次试验采用尺寸为240 mm×115 mm×53 mm的MU10烧结普通砖，砌筑砂浆和抹面砂浆分别按M7.5、M10的水泥砂浆配制，构造柱混凝土按C25配制。

试验中HDC采用的配合比为：水泥∶粉煤灰∶砂∶水=1∶1∶0.72∶0.58，其中水泥为P·O 42.5R普通硅酸盐水泥，砂为西安灞河精细河砂，最大粒径为1.18 mm，粉煤灰为河南省某电厂的Ⅰ级灰，减水剂为萘系高效减水剂。PVA纤维的体积掺量为2%，各项性能指标见表2。

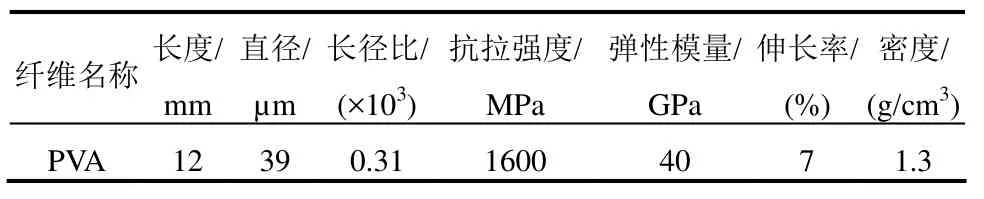
表2 PVA纤维各项性能指标Table 2 Performance indicators of PVA

根据《砌墙砖试验方法》(GB/T 2542―2003)的要求，制作了10个单砖试样，测得烧结普通砖的抗压强度平均值为8.87 MPa；采用70.7 mm×70.7 mm×70.7 mm立方体试块测得砌筑砂浆和抹面砂浆的抗压强度平均值分别为18.11 MPa、27.62 MPa；采用100 mm×100 mm×100 mm立方体试块测得构造柱混凝土的抗压强度平均值为37.89 MPa；采用70.7 mm×70.7 mm×70.7 mm立方体试块测得HDC抗压强度平均值为58.70 MPa。

1.3 加载装置及加载制度

加载装置包括水平荷载和竖向荷载两部分加载系统，如图2所示。水平加载点位于试件加载梁端部的截面中心，水平荷载由100 t往复作动器提供，作动器前端连接单向铰，可保证水平加载方向的稳定性，作动器前端与水平连接装置相连，通过水平连接装置对墙体施加水平往复推拉荷载；竖向加载点位于墙顶中心处，竖向荷载由200 t油压千斤顶施加于刚性垫梁上，以使墙体截面均匀受压。

试验中共安设5个测点，墙体的剪切变形通过沿45°对角线方向各安装的一个百分表进行测量；在试件顶部加载梁中心布置一个位移计，以测量其水平位移；在墙体底部截面两端各安装一个百分表，以测量其截面的转角。将往复作动器前端的拉压荷载传感器和试件顶部位移计传感器连接到动态电阻应变仪上，通过X-Y绘图仪同步绘制试件的荷载-位移曲线。

根据《建筑抗震试验方法规程》[20]的规定，拟静力试验加载程序采用荷载-变形双控制的加载程序。根据西安市长安区实际工程中某4层教学楼，计算得到底层墙体的竖向压应力约为1.22 MPa(440 kN)，以此作为本次试验中各试件施加的竖向荷载。竖向荷载在试验前一次加足，加载过程中竖向荷载保持不变。试验前先预加预估开裂荷载的20%反复推拉2次，检查仪表正常后，开始正式加载。试件屈服前采用荷载控制分级加载，按40 kN递增，每级荷载下反复推拉一次；试件开裂后采用位移控制，按假定屈服位移yΔ加载，每级位移下反复推拉3次，直至水平荷载下降为峰值荷载的85%。

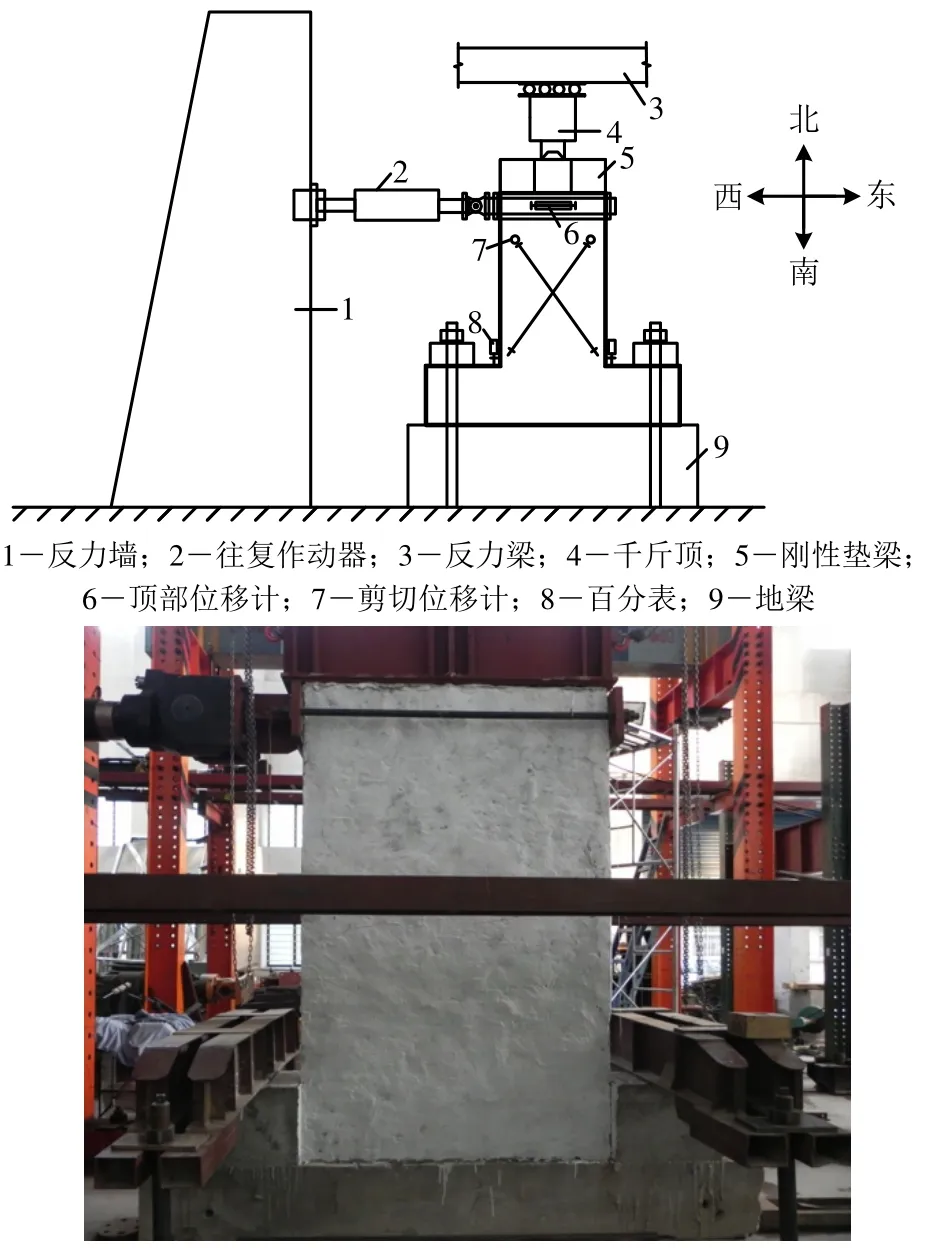
图2 加载装置Fig.2 Test setup

2 试验结果及分析

2.1 试件破坏过程及形态

1) 试件W1

在试件W1加载过程中，当水平荷载加载到80 kN时，墙体脚部砌体受压开裂，两端均出现竖向微裂缝；加载到120 kN时，墙体下部受压开裂而发出轻微的响声，墙体根部沿水平通缝弯曲受拉开裂；加载至160 kN时，试件变形增大，荷载-位移曲线明显偏离直线，试件开始屈服，以此对应的墙体位移作为假定屈服位移yΔ，改为按位移控制加载。

按位移加载至-9 mm(160 kN)时，墙体底部水平裂缝迅速变宽延长；推至12 mm时，水平弯曲裂缝贯通，墙体底部产生水平剪切滑移；推至16 mm时，试件西侧墙体下部竖向裂缝延伸变宽；拉至-18 mm时，试件东侧墙脚处部分砖块压碎脱落，同时产生数条新的竖向裂缝；推至22 mm时，试件底部出现明显的整体水平错动；拉至-30 mm(120 kN)时，试件底部平面外出现明显的水平错动，墙脚处砖块局部压碎，荷载下降至峰值荷载的85%以下，试件发生弯曲破坏，底部出现明显的水平剪切滑移裂缝。试件W1的最终破坏形态及裂缝分布见图3。

图3 试件W1破坏形态和裂缝分布Fig.3 Damage patterns and crack distribution of W1

2) 试件W2

加载初期无明显变化；当水平拉力达到-80kN时，试件东侧墙脚处出现1条细微斜裂缝；推至120 kN时，试件西侧墙脚处出现1条竖向微裂缝及数条细微斜裂缝；拉至-120 kN时，试件东侧墙脚处斜裂缝向墙体底部延伸；推至160 kN时，试件西侧墙脚处主斜裂缝宽度增至约2 mm，墙体下部出现数条新的斜裂缝；拉至-160 kN时，试件东侧墙脚处斜裂缝发展为水平弯曲裂缝。荷载-位移曲线明显偏离直线，改为按位移控制加载。

按位移加载至8 mm(160 kN)时，试件西侧墙脚处主斜裂缝急剧变宽，约5 mm；拉至-10 mm时，试件东侧墙脚处主斜裂缝向下延伸；推至11 mm时，试件西侧墙脚处主斜裂缝发展至墙体底部后向水平方向延伸；拉至-13 mm时，试件底部的弯曲裂缝发展贯通；推至17 mm时，试件西侧墙脚处砂浆面层明显外鼓、剥离；拉至-22 mm时，墙体脚部水泥砂浆面层压碎脱落。推至29 mm时，墙底截面端部破坏严重，水泥砂浆面层大面积剥落，竖向钢筋明显压屈；拉至-31 mm(136 kN)时，墙底截面端部砖块被压碎，承载力急剧下降，试件底部发生弯曲破坏，上部墙体基本完好。试件W2的最终破坏形态及裂缝分布如图4所示。

3) 试件HDC-W1

图4 试件W2破坏形态和裂缝分布Fig.4 Damage patterns and crack distribution of W2

当水平荷载推至120 kN时，墙脚处截面两端水泥砂浆面层出现多条水平裂缝，但HDC面层未见开裂。推至160 kN时，试件西侧墙脚处HDC面层出现细微斜裂缝。拉至-160 kN时，试件东侧墙脚处水泥砂浆面层的斜裂缝急剧变宽，向墙底延伸。荷载-位移曲线明显弯曲，改为按位移控制加载。

推至9 mm(160 kN)时，墙根处水泥砂浆面层的斜裂缝急剧变宽，最大裂缝宽度达8 mm，HDC面层的主斜裂缝沿水平方向发展。拉至-15 mm时，墙根处水泥砂浆面层局部压碎脱落，HDC面层保持良好的完整性。推至21 mm时，墙根处水泥砂浆面层一侧水平裂缝发展贯通，HDC面层局部外鼓；拉至-21 mm时，水泥砂浆面层一侧墙底砖块局部压碎脱落。推至27 mm时，墙根处HDC面层出现局部剥离。推至30 mm时，墙脚处水泥砂浆面层和砖块破碎脱落，荷载降至峰值荷载的85%以下，停止加载。试件HDC-W1的最终破坏形态及裂缝分布见图5。

图5 试件HDC-W1破坏形态和裂缝分布Fig.5 Damage patterns and crack distribution of HDC-W1

4) 试件HDC-W2

加载初期无明显变化，当推至160 kN时，墙脚处出现数条细微斜裂缝。卸载后有残余变形，试件进入弹塑性阶段，开始按位移控制加载。

按位移加载至9 mm时，墙脚处主斜裂缝向砖墙下部发展延伸，新增数条细微斜裂缝。推至15 mm时，墙脚处主斜裂缝发展至墙体底部后向水平方向延伸。推至18 mm时，墙体底部HDC面层局部外鼓，HDC面层开裂处砖块均被拉裂。加载至24 mm时，墙体脚部砖块局部压碎，HDC面层开始剥离。推至39 mm时，砖块局部破碎脱落，内部砖墙受损严重。加载至42 mm(130 kN)时，墙体受损严重，承载力明显下降，停止加载。试件HDC-W2的最终破坏形态及裂缝分布见图6。

图6 试件HDC-W2破坏形态和裂缝分布Fig.6 Damage patterns and crack distribution of HDC-W2

5) 试件HDC-W3

试件HDC-W3的破坏过程和裂缝分布与试件HDC-W2相似，当加载至120 kN时，墙脚处出现多条细微斜裂缝。加载至180 kN(顶点位移6 mm)时，墙脚处主斜裂缝向下延伸至墙底，荷载-位移曲线明显弯曲，改为按位移控制加载。

推至13.5 mm(248 kN)时，窗间墙下部主斜裂缝向水平方向延伸；拉至-19.5 mm(235 kN)时，主斜裂缝发展变宽。推至31.5 mm时，墙根部裂缝处HDC面层局部外鼓；拉至-37.5 mm时，墙脚处砖块局部压碎，墙底部HDC面层开始剥离。加载至46.5 mm(148 kN)时，砖块局部破碎脱落，内部砖墙受损严重，承载力明显下降，停止加载。试件HDC-W3的最终破坏形态及裂缝分布如图7。

2.2 破坏机理

从上述破坏过程可以发现，5片受弯无筋砌体墙的试验结果具有以下特点和规律：

1) 试件W1的破坏过程为：墙脚处砌体受压首先出现竖向裂缝；随后墙根部出现水平弯曲裂缝并迅速延伸贯通，使墙体产生水平剪切滑移；最后墙体根部砖块局部压碎。试件W1发生弯曲破坏[2]。

图7 试件HDC-W3破坏形态和裂缝分布Fig.7 Damage patterns and crack distribution of HDC-W3

2) 钢筋网水泥砂浆面层加固的试件W2破坏过程为：加载初期，墙脚处产生数条细微斜裂缝；随后斜裂缝急剧变宽，延伸至墙体底部后沿水平方向发展；最后受压侧墙脚处水泥砂浆面层局部剥离，竖向钢筋压屈，墙体根部砖块大面积破碎脱落，试件发生弯曲破坏。

3) 采用HDC面层加固的试件HDC-W1、HDC-W2、HDC-W3破坏的共同特点为：① HDC面层良好的拉伸硬化和抗剪切性能与砖墙具有一定的协同工作能力，采用HDC面层加固的砖墙始终未出现大面积的HDC面层脱落；② 采用HDC面层加固的砖墙抗裂性能明显提高，其主斜裂缝均出现在墙脚处和墙下部；③ 试件破坏过程中，HDC面层对砖墙形成约束作用，使内部砖墙具有较好的整体性；④ 试件破坏时，墙脚处的HDC面层局部剥离，砖块局部压碎脱落，试件最终均发生弯曲破坏。

通过对比分析可知：未加固试件发生了摇摆破坏，砖块局部压碎，底部出现沿水平灰缝的弯曲裂缝，表现出明显的脆性破坏特征。钢筋网水泥砂浆面层加固试件发生典型的弯曲破坏，底部的弯曲裂缝发展贯通，且面层压碎脱落，端部破坏严重。HDC加固试件最终均发生弯曲破坏，主斜裂缝均出现在墙脚处和墙下部。HDC面层未出现大面积的剥落，对砖墙有一定的约束作用，减小了墙体的损伤程度。

2.3 滞回特性

本次试验中5片受弯砖墙的荷载-位移滞回曲线如图8所示，其滞回特性如下：

1) 5片受弯砖墙均表现出弯曲破坏的特性，完全卸载后，墙体下部的弯曲裂缝未能完全闭合，存在一定的残余变形。随着每一级循环加载下主裂缝的往复张开和闭合，5片墙体的滞回曲线都产生了一定的捏拢现象，滞回环明显呈反S形，试件的弯曲裂缝开展越宽，捏拢现象越明显。

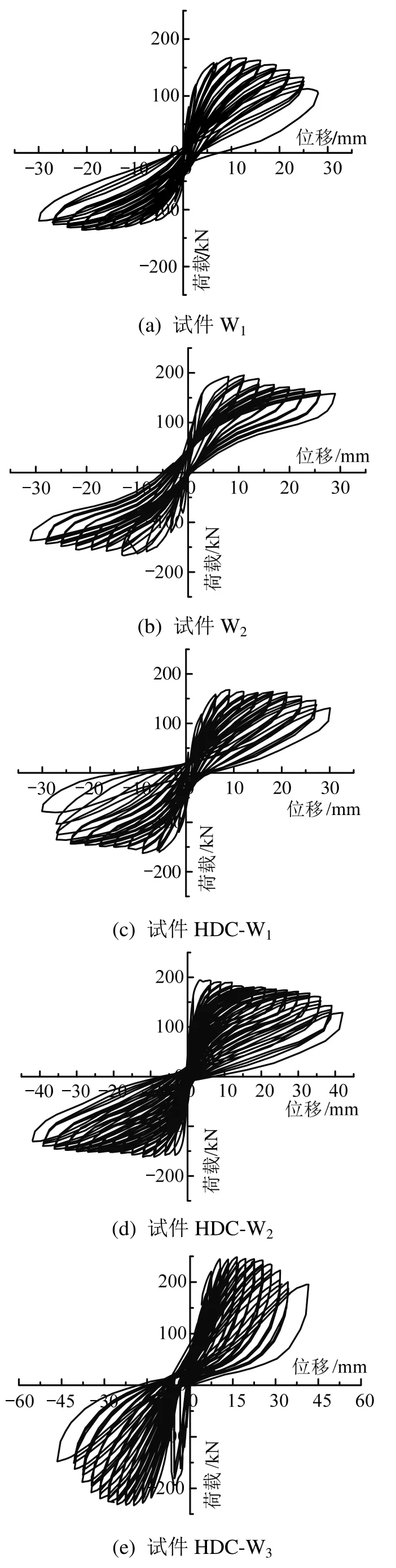
图8 荷载-位移曲线Fig.8 Load-displacement curves of specimens

2) 试件W1和W2的滞回环、加载循环次数无明显变化，说明钢筋网水泥砂浆面层加固未能显著改善该砖墙的变形性能。与试件W1相比，试件HDC-W1和HDC-W2的滞回曲线更饱满，循环加载次数明显增多，表明HDC面层加固的砖墙具有更好的耗能能力。对比试件W2和HDC-W2，后者的滞回环明显更饱满，可见HDC面层加固的墙体表现出了更好的耗能能力和变形能力。试件HDC-W3的滞回曲线比试件HDC-W2更为饱满，说明构造柱可较大幅度提高受弯墙体的耗能能力。

2.4 骨架曲线

根据荷载-位移滞回曲线绘制出5个试件的骨架曲线，如图9所示。以墙体出现明显的裂缝确定开裂位移和开裂荷载；以骨架曲线上最大荷载点对应的荷载和位移确定峰值荷载与峰值位移；根据各试件的骨架曲线，采用“通用屈服弯矩法”确定屈服位移；以骨架曲线上承载力下降到85%峰值荷载对应的点确定极限位移，延性系数为极限位移与屈服位移之比，极限位移角为极限位移与墙体高度之比。各试件的特征点和位移延性见表3。通过图9和表3比较分析，可知：

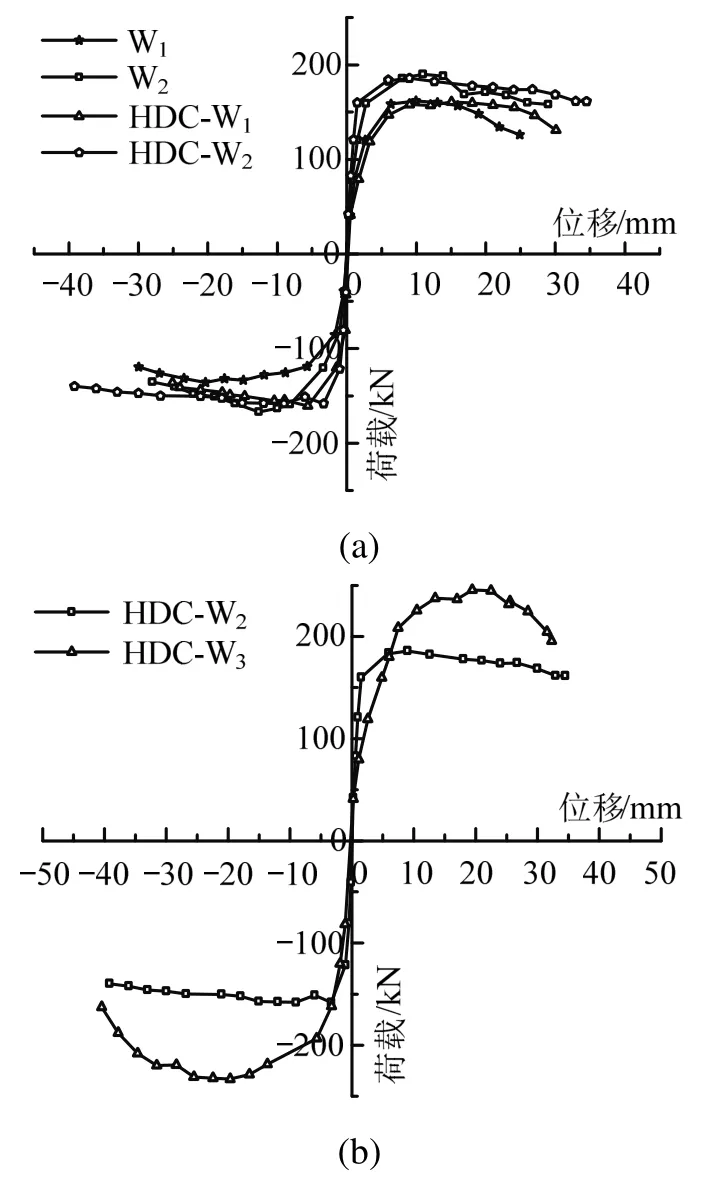
图9 骨架曲线Fig.9 Skeleton curves

1) 5片发生弯曲破坏的受弯砌体墙均表现出较好的延性，试件HDC-W1、HDC-W2的位移延性系数和极限位移分别高于试件W1为15%～49%和52%～112%，表明采用HDC面层加固受弯无筋砖墙可抑制墙体内部裂缝的开展，显著改善受弯砌体墙的延性。

2) 试件HDC-W1、HDC-W2的开裂位移、屈服位移、极限位移和延性系数均高于试件W2，说明采用HDC单面和双面面层加固的受弯砖墙变形能力均优于钢筋网水泥砂浆面层加固的砖墙。

3) 试件HDC-W3的极限位移角和延性系数与试件HDC-W2接近，峰值荷载提高35%，说明砖墙发生弯曲破坏时，中部设置构造柱可提高砖砌体墙的承载力，但变形能力提高作用有限。

2.5 承载力分析

由于加载时推、拉方向的荷载不一致，故荷载取2个方向荷载的平均值。本次试验5片受弯砖墙的开裂荷载和峰值荷载见表3，可知：

1) 试件W1和W2的开裂荷载接近，但试件HDC-W1、HDC-W2、HDC-W3的开裂荷载均有较大幅度提高，说明HDC面层可有效抑制受弯无筋砌体墙的开裂和破坏，提高墙体的整体性。

2) HDC面层加固厚度仅为钢筋网水泥砂浆面层的0.4倍，但试件HDC-W2的极限荷载仅为试件W2的0.98倍，说明HDC面层可有效提高受弯无筋墙体的抗震承载力，且HDC面层施工更为简便。

3) 试件HDC-W3比HDC-W2的承载力提高35%，说明墙体中部设置构造柱能显著提高受弯墙体的抗震承载力。

2.6 耗能能力分析

本试验中5片砖墙的累积滞回耗能见表4，列出了试件达到屈服荷载、极限荷载和破坏荷载时的累积耗能，可反映结构构件在不同性能水平下的耗能能力。从表4可知：

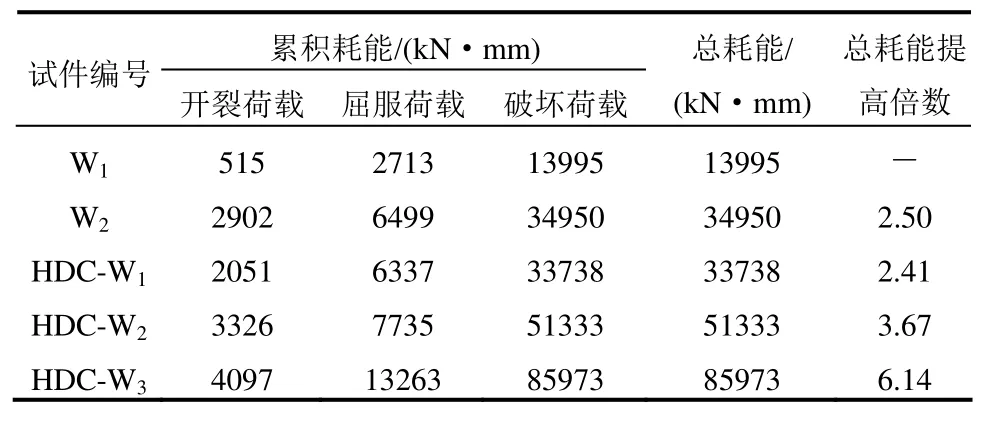
表4 试件的累积耗能Table 4 Cumulated energy dissipation of specimens

1) 试件HDC-W1、HDC-W2的总耗能分别比未加固试件W1提高2.41倍和3.67倍，可见采用HDC面层加固后砖墙的耗能能力得到较大幅度提高。

2) 试件HDC-W1的总耗能与试件W2接近，且试件HDC-W2比试件W2提高1.47倍，说明采用HDC双面加固砖墙的耗能能力优于钢筋网水泥砂浆面层加固砖墙。

3) 试件HDC-W3比HDC-W2的总耗能提高1.67倍，说明墙体中部设置构造柱能显著改善受弯墙体的耗能能力。

2.7 刚度退化

根据荷载-位移曲线计算出每一级荷载下各试件的割线刚度，绘制出刚度退化曲线，见图10。由图10可见，5个试件刚度退化的共同特点为：加载初期，初始刚度急剧下降；随着荷载的增加，刚度退化趋于平缓；最后试件的刚度基本保持稳定。通过比较分析，可以得出：

1) HDC面层加固后砖墙的初始刚度均高于未加固试件W1，其刚度退化趋势比较平缓，主要由于HDC面层良好的拉伸性能和耐损伤能力，试件出现裂缝后仍能继续承受较大的水平荷载。

2) 采用HDC单面加固的试件HDC-W1的刚度退化曲线与试件W2接近，但试件HDC-W2的刚度退化更平缓，说明HDC面层能显著改善砖砌体墙的脆性破坏特征，加固后其变形性能优于钢筋网水泥砂浆面层。

3) 试件HDC-W3比HDC-W2刚度退化缓慢，说明无筋砌体墙发生弯曲破坏时，墙体中部设置构造柱可在一定程度上提高砖墙的耐损伤能力。

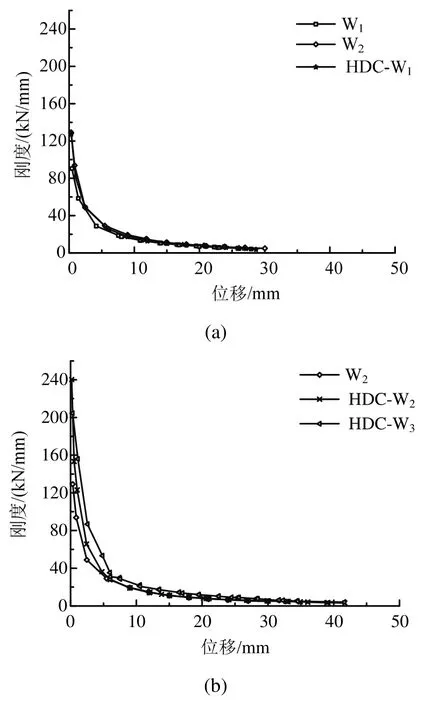
图10 刚度退化曲线Fig.10 Stiffness degradation curves

3 性能指标

3.1 性能水平确定原则

为了与我国建筑抗震设计规范[21]“小震不坏、中震可修、大震不倒”的三水准设防目标相协调，参考建筑地震破坏等级划分标准[22]将HDC加固受弯无筋砌体墙划分为3个性能水平：使用良好(DS1)、人身安全(DS2)和防止倒塌(DS3)。考虑到HDC加固的受弯无筋砌体变形和耐损伤性能有较大提高，且位移角与构件的损伤程度有较高的相关性，本文提出采用位移角作为其性能水平的量化指标。各性能水平的确定原则：以试件HDC加固层出现第1条明显裂缝确定“使用良好”性能水平；以试件屈服后，HDC面层上的主斜裂缝延伸变宽，面层局部外鼓，确定“人身安全”性能水平；以砖块压碎剥落，面层剥离，或水平承载力下降≯10%确定“防止倒塌”性能水平。

3.2 性能指标统计分析

为便于实际工程中确定HDC面层加固砌体墙的位移角限值，对本课题组完成的HDC面层加固砌体墙的试验数据[13－15]进行统计分析。试件竖向荷载试验值范围为0.3 MPa ～ 1.22 MPa，高宽比范围为0.6～1.2，加固方式包括单面和双面HDC加固。以上13个试件各性能水平所对应的位移角见表5。

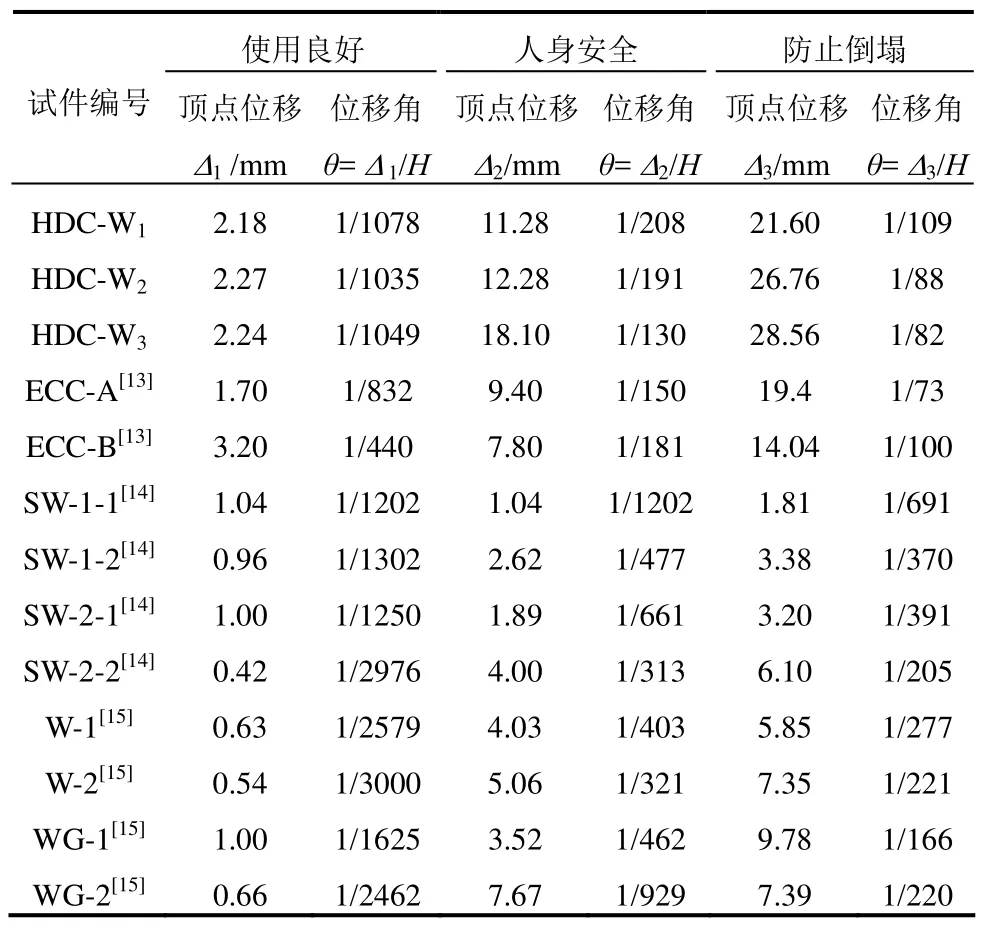
表5 试件的性能指标量化值Table 5 Performance indexes of specimens

由表5可见，使用良好性能水平状态的位移角分布为1/3000～1/440，其中位移角在1/1700～ 1/1000的试件数量最多，占到试件总量的54%，而位移角＞1/1000的试件仅有试件ECC-A和ECC-B。对于人身安全性能水平状态的位移角分布为1/1202～1/130，其中位移角在1/350～1/150的试件数量最多，占到试件总量的62%，而位移角＞1/150的试件只有HDC-W3，因为相比于同尺寸试件，该墙体中部设置了构造柱，变形能力有所提高。防止倒塌性能水平状态的位移角分布范围为1/691～1/73，其中位移角在1/300～1/70的试件数量最多，占到试件总量的77%，而位移角＜1/300的试件只有SW-1-1、SW-1-2和SW-2-1，因为文献[14]中的砖墙为单面加固，位移角小于双面加固构件。

以上分析可知，试件之间的位移角有一定的离散性，尤其是构件初裂时的位移角，这与加载时墙体的竖向应力、HDC的加固方式、砖墙的高宽比和砌体类型有关。考虑到上述不确定因素影响，参考约束砌体基于位移角的易损性评估方法[23]，将试件各性能水准下的位移角以升序进行排列，则第j个试件在dsi水准状态下位移角大于θ的概率为：

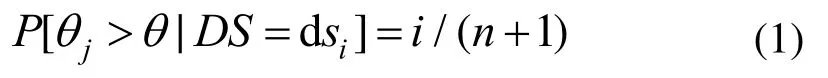
式中：i为位移角在升序中的位置；n为样本个数。由于正态累积分布的2个参数期望值μ和标准差σ能较好的反应数据的中心趋势和离散程度，因此本文对样本数据采用正态累积分布。那么，试件在位移角为θ时大于损伤状态dsi的条件超越概率为：

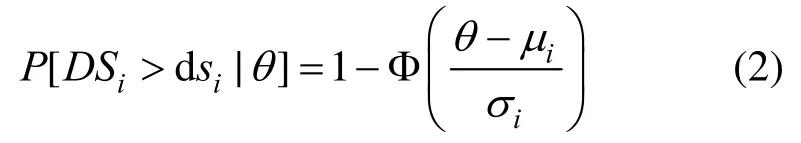
式中：Φ为标准正态累积分布；μi和σi分别为试件在dsi状态时概率函数的期望值和标准差，且可通过增加样本容量减少这两个参数的误差。度量拟合优度的可决系数(R-square=0.9233)均接近于1，说明正态累积分布适用于本文的样本数据。

3.3 基于位移角的易损性曲线

HDC加固砌体墙在三个性能水平下基于位移角的易损性曲线见图11，根据该曲线选择不同性能水平下具有相同超越概率的位移角限值。例如，图11中平行于X轴的直线a代表超越概率等于50%的基准线，可得超越概率P[DS＞ds]=0.5时，HDC加固的砌体结构使用良好、人身安全和防止倒塌性能水准的位移角限值分别为1/1362、1/299、1/161；平行于x轴的直线b代表超越概率=30%的基准线，可得超越概率P[DS＞ds]=0.3时，HDC加固的砌体结构使用良好、保证人身安全和防止倒塌性能水准的位移角限值分别为1/1946、1/494、1/245。

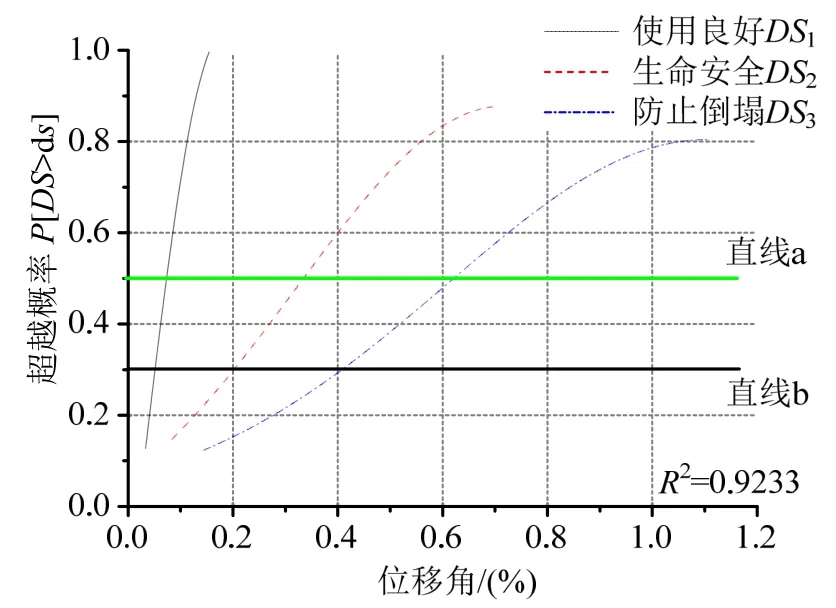
图11 基于位移的超越概率回归曲线Fig.11 Drift-based exceedance probability curves

依据HDC加固砌体墙基于位移角的易损性曲线，可在实际工程中灵活选取具有不同超越概率的位移角限值，为HDC加固砌体墙基于位移的性能设计提供了性能指标的取值依据。考虑到统计分析的样本数量有限，各性能水平所对应的位移角仍需根据大量试验结果进一步修正。

本文HDC加固受弯砌体墙在3个性能水平下的位移角范围分别为：使用良好，1/1078～1/1035；人身安全，1/191～1/130；防止倒塌，1/109～1/82。可见，HDC加固受弯无筋砌体墙的位移角均大于超越概率为30%的位移角限值，采用HDC面层加固可减小该类试件的损伤风险。以上分析表明，HDC面层加固方法可显著改善受弯砌体墙的变形和耐损伤能力。