非连续变形分析的若干问题
2020-03-16凌道盛巩师林胡成宝钮家军
凌道盛,巩师林,胡成宝,钮家军
(1.浙江大学岩土工程研究所,浙江,杭州 310058;2.浙江大学软弱土与环境土工教育部重点实验室,浙江,杭州 310058;3.浙江大学宁波理工学院土木建筑工程学院,浙江,宁波 315100)
包含大量孔隙、节理甚至断层的非连续岩土体结构在自然界中广泛存在,岩土体的非连续变形分析日益引起人们的关注。石根华[1-2]提出的非连续变形分析方法(discontinuous deformation analysis,DDA)是非连续变形分析中最有效的方法之一[3-4],已经广泛应用于地震引起的山体滑坡分析、岩石爆破过程模拟、落石轨迹追踪、隧道及采矿、岩石边坡稳定性评价及其他方面[5-12]。
原始DDA假设块体满足小应变、大转动,将块体位移增量分解为常应变对应的变形、刚体平动和刚体转动三部分之和,即位移增量分量直接相加。求解时以上一时步构型作为参照构型,在时间步内将块体位移增量线性化,并利用求得的线性化位移增量更新块体构型。研究表明,原始DDA的位移模式采用全一阶近似和小角度假定,导致块体体积自由膨胀、应变分量物理意义不明确、应力场畸变等问题[13],给数值计算带来较大误差。同时,采用一阶近似后的位移模式推导块体相关加速度表达式,忽略了块体转动时离心力与科氏力的作用。针对上述问题,MacLaughlin等[14]将一阶近似前位移公式中余弦值二阶泰勒级数展开,当每时步转角小于 0.4 rad时块体体积自由膨胀产生的误差可以接受。Cheng等[15]以转角增量的正弦作为基本未知量,基于三角函数恒等式改写了有限转动位移增量公式,并利用上一时步转角的增量简化形函数矩阵,一定程度上克服了块体体积不合理膨胀现象,在块体匀速转动时可获得精确解。Ke[16]及Koo等[17]在每一时步计算完成后采用有限转动位移公式对块体位移进行后修正(post-adjustment)。高亚楠等[18]采用有限变形理论将块体运动过程分解为变形和转动两部分,并根据有限变形几何场更新块体构型,可消除块体转动带来的自由膨胀。Jiang等[19]在每一块体中固定随动坐标系,应变分量增量仅在随动坐标系下叠加,利用有限转动位移全量公式计算块体全量位移,更新当前构型,避免了块体大转动时的虚假体积膨胀及应力场畸变。Lin等[20]基于Green应变和第二类 Piola-Kirchhoff应力,给出采用二阶多项式导出的块体有限变形公式,可模拟大应变、有限转动问题。Fan等[21]将块体的运动进行S-R(strain-rotation)分解以同时获取块体的变形与转动,采用原有DDA的形函数构造控制方程,克服了块体体积自由膨胀问题,并赋予其处理大变形问题的能力。
综上可见,现有DDA及其改进方法大都基于原始DDA的位移模式及构型更新方法,在此基础上,本文分析了原始DDA存在的若干问题,包括小角度假设及线性化位移增量导致的块体体积膨胀、应变分量直接叠加导致的应变场畸变及其物理意义不明确以及采用线性化后的位移增量公式推导块体的加速度导致忽略块体旋转的离心力和科氏力作用。通过算例证实了上述若干问题的存在,为DDA的进一步发展,从而为真实准确地模拟岩土工程中的具体问题提供参考。
1 原始DDA位移模式
石根华提出的 DDA假设块体为常应变,且满足小变形假设。不失一般性,假定tn时刻块体的构型已知,物质点 {X,Y}T的空间坐标为 {xn,yn}T。以tn时刻为参照构型,从tn时刻到tn+1时刻的位移增量{Δun, Δvn}T可分解为三部分,即刚体平动、绕参考点的刚体转动和常应变对应的变形。根据原始DDA的表述,位移增量由上述三部分直接叠加,表示为:

DDA的研究对象以岩石为主,在小应变、小转动假设的前提下,块体的几何方程表示为:
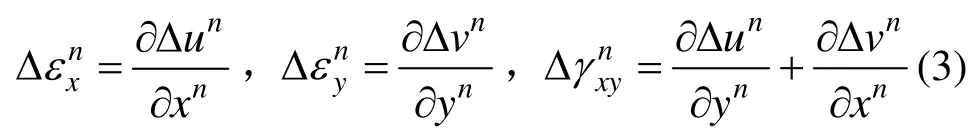

块体在满足小变形、小转动假定后,式(1)、式(2)可线性化为:

将上式,采用矢量形式表示:

式中,Tn、 Δdn分别为块体在tn时刻的形函数矩阵与广义位移矢量增量。分别表示为:
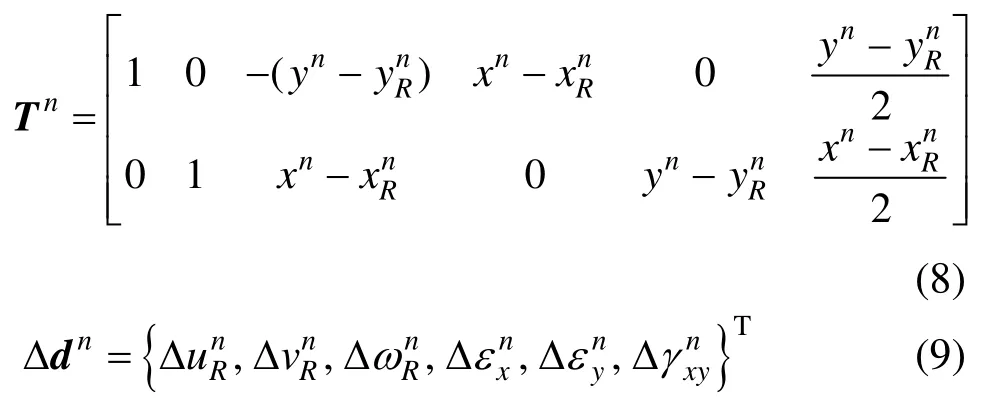
类似地,tn+1时刻块体内任意物质点的加速度表示为:

式中,圆点顶标“⋅⋅”表示物理量关于时间的二阶导数。
开闭迭代求得块体广义位移增量后,原始DDA通过简单累加求得tn+1时刻块体的广义位移矢量总量dn+1和块体任意点位移un+1:
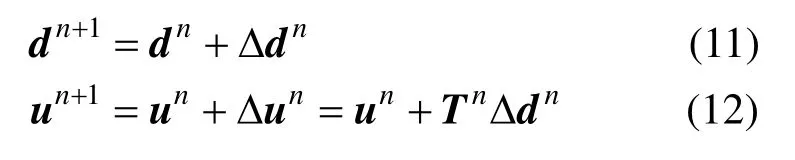
2 原始DDA存在的若干问题
2.1 转角增量的一阶近似导致大转动时块体体积自由膨胀
建立在小变形、小转动假设之上的原始 DDA在模拟边坡滑动、岩石崩塌等实际工程灾害时,作为研究对象的块体常涉及大转动问题,此时会观察到块体体积出现不合理膨胀现象。
在tn时刻,块体中任意点P{xn,yn}T绕参考点沿着x轴、y轴位移增量的精确解{Δun, Δvn}T,见式(1)、式(2)。假定研究对象为刚体,此时:
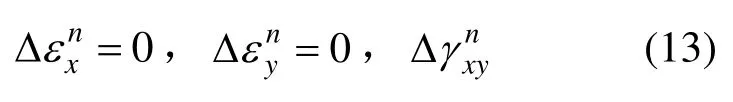
式(1)、式(2)可简化为:
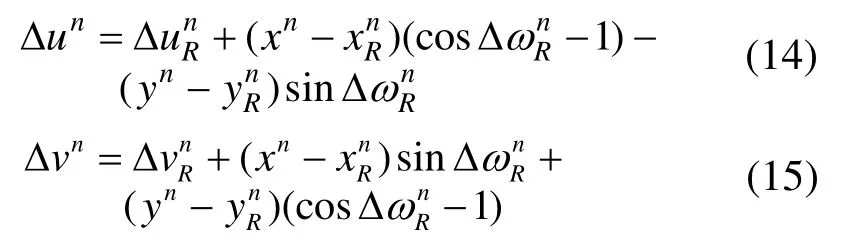
式(5)、式(6)简化为:

将刚体转动位移增量精确解式(14)、式(15)和近似解式(16)、式(17)进行几何对比,如图1所示,线段P0P旋转后长度为P0P′,且P0P=P0P′。而小角度假定条件下的近似解P0P′导致线段沿着r向量发生偏移,此时P0P<P0P′。当每时步内的转角增量较大时,误差逐步累积,最终导致块体体积产生自由膨胀。
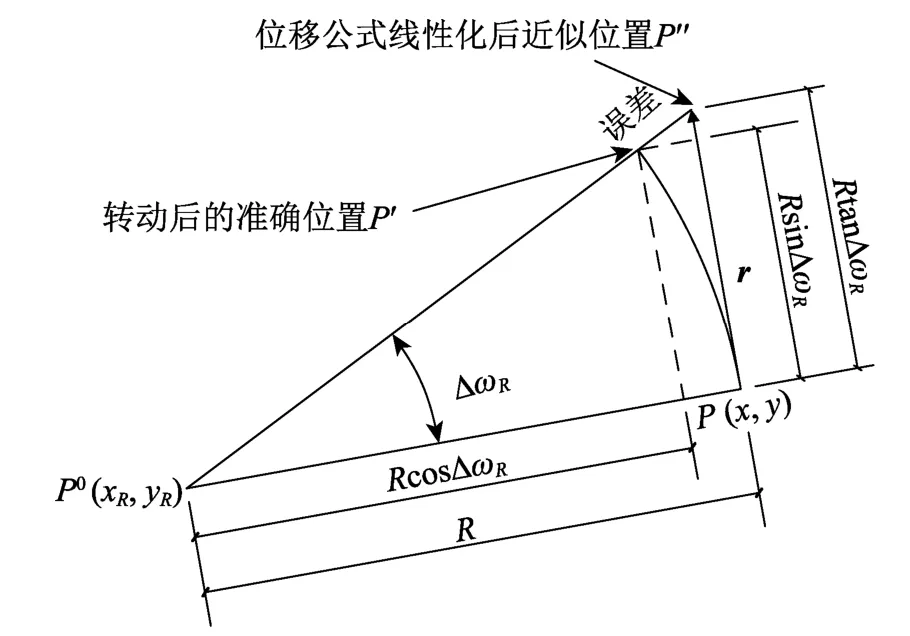
图1 刚体转动位移精确解与近似解几何图Fig.1 Gemetry of approximation and the exact solution to rigid block rotation
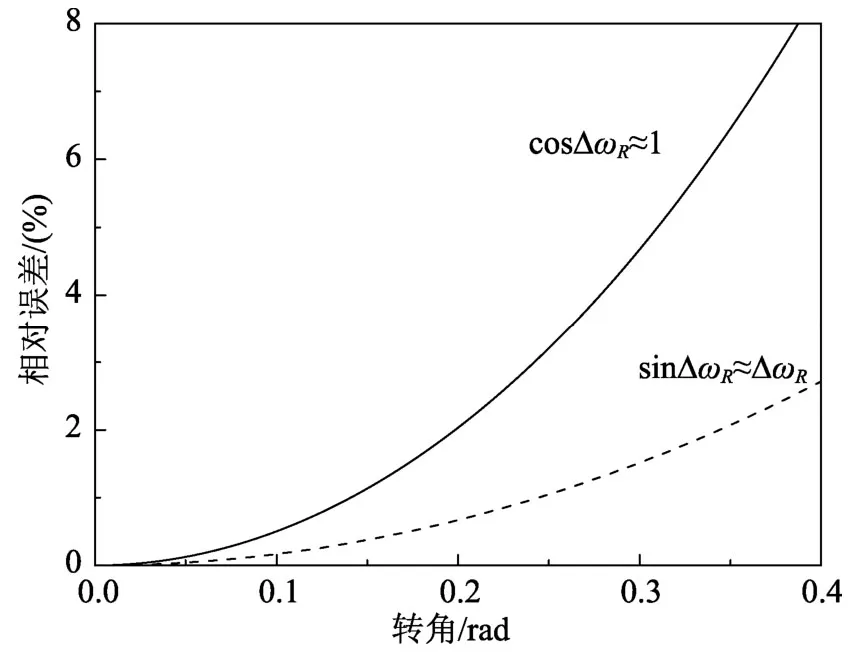
图2 小角度假设的相对误差Fig.2 Relative error induced by small rotation assumption
2.2 应变增量的直接叠加导致块体应力、应变场畸变
现阶段,针对原始DDA采用线性化位移增量更新块体构型引起的块体体积自由膨胀现象,一些学者提出了不同的修正方法。虽然不同修正方法可在一定程度上克服块体体积的自由膨胀,但是模拟块体大转动问题时,块体应力及应变计算仍会引入较大误差。
原始DDA模拟的块体发生有限转动时,开闭迭代结束后得到的变形变量增量Δd可分为两类。一类是当块体发生有限转动时可直接叠加的水平和竖向位移增量以及刚体转角增量以上三种块体的变形变量分量的增量当块体发生有限转动时可直接叠加。另一类为小应变假设前提下,块体另外三项应变相关的变形变量分量的增量在块体发生有限转动时,应变分量增量的直接叠加会带来明显的误差。
而原始DDA及大多数修正后的DDA程序在开闭迭代后,应变分量增量直接叠加获得应变分量总量,即:
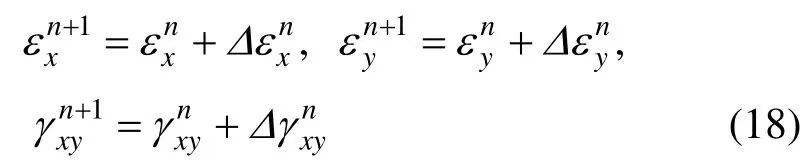
假定块体为线弹性体,原始DDA根据块体应变求得应力,并将求得的应力作为块体初始应力加到总体平衡方程中去。在平面应力条件下,nt时刻应力-应变关系满足:

式中:E、μ分别为块体的弹性模量及泊松比;{σx,σy,τxy}nT及 {σx,σy,τxy}n-1T分别为tn、tn-1时刻的块体应力分量总量。
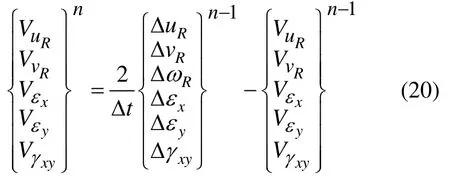
同样,原始DDA中每时步的初速度为上一时步结束后的末速度,在时间步长为Δt条件下,块体在tn时步内的速度与tn-1时步内的速度有如下关系:
然而,开-闭迭代后求得的应变分量增量均是基于局部坐标系,即图 3(b)中的X′OY′坐标系。若应变分量增量直接进行叠加而不作坐标系旋转,不同时步应变增量的参照构型不同,块体内应变物理意义不明确。且若将块体的应变限制为0,由式(19)、式(20),当块体旋转时,块体内应力场及速度场将产生畸变。

图3 块体应变示意图Fig.3 Sketch of block strain
2.3 采用加法分解的位移增量公式忽略块体旋转过程中的离心力与科氏力
Jiang在原始DDA基础上,在每个块体中固定随动局部坐标系,开闭迭代后求得的应变增量分量旋转至局部坐标系下叠加,并采用有限转动位移总量公式计算块体总位移,更新块体构型。不仅克服了大转动时块体体积的自由膨胀,而且避免了块体应变的累计误差,计算出的应变更为合理。
DDA通过选取不同动力系数gg(gg=0~1),即块体当前时步的初速度与上一时步末速度的比值,可同时处理静力学与动力学问题。对于动力学问题,块体运动过程中的惯性项不可忽略。DDA将加速度引起的惯性力考虑在内,并表示为:

在块体位移增量精确表示式(1)、式(2)的基础上,原始DDA基于小角度假设,将式(1)、式(2)一阶近似为式(5)、式(6),并以一阶近似后的式(5)、式(6)推导块体相关子矩阵。惯性力子矩阵的推导与块体加速度有关,而原始DDA中块体加速度由式(5)、式(6)直接导出,即:
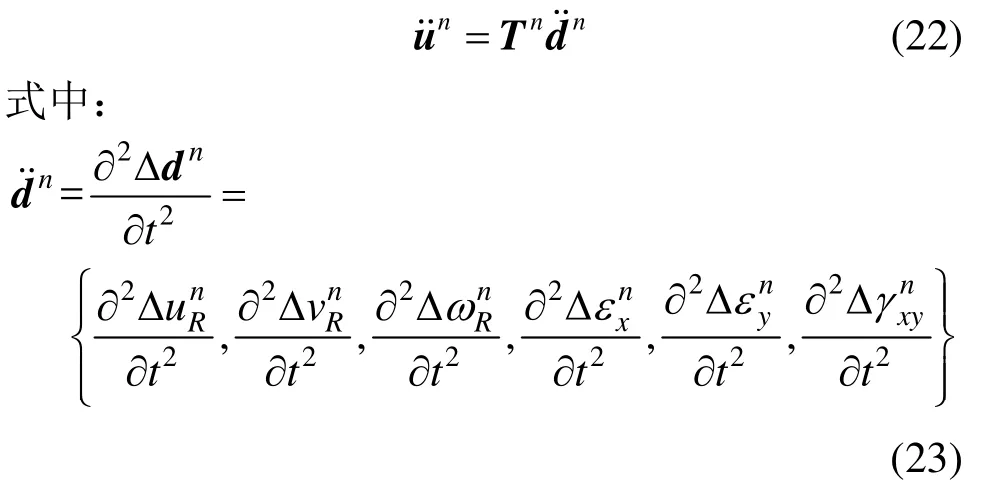
块体旋转过程会产生离心力及科氏力,原始DDA采用一阶近似后的线性表达式推导块体的加速度表达式,而块体加速度应是从线性化前的位移增量表达式导出后再线性化,直接采用线性化后的位移增量表达式忽略了块体旋转时离心力和科氏力的作用。
3 算例验证
设计两个典型算例来说明原始 DDA采用一阶近似后的位移增量简单叠加并推导块体相应的加速度表达式,及开闭迭代后应变增量的直接叠加,在模拟块体大转动时带来的相关问题。
3.1 正八边形绕定点摆动问题
如图4所示,对角线长10 m、绕顶点E摆动的正八边形,质量密度为 2800 kg/m3,弹性模量为2 GPa,泊松比为0.25。以八边形质心为坐标原点O,如图示建立坐标系XOY。
采用一个块体模拟重力作用下八边形绕顶点E的摆动,取时间步长Δt=0.002 s。图 5给出了原始DDA程序计算的该八边形面积随计算时步的变化曲线。由图 5可见,随着计算时步的增加,原始DDA计算出正八边形面积发生较大膨胀,该正八边形的初始面积为70.7 m2,计算到5000步时,面积已经达到72.4 m2,膨胀了2.45%,这一误差在工程分析中是不可接受的。
表1给出了正八边形块体在200步、2000步及5000步时,四条对角线长度变化及相应的线应变,表2给出相应时步块体应变及主应变计算的结果。

图4 正八边形块体绕固定点摆动Fig.4 A swing regular octagon fixed at one vertex point

图5 八边形面积随计算时步变化曲线Fig.5 Change of octagon area with time step

表1 原始DDA计算的各对角线长度及应变Table 1 The length changes of four segments on the swing octagon by original DDA
由表1可得,随着计算时步的增加,当计算至5000步时,四条对角线伸长量均较大,对应的线应变均在1.2×10-2。而5000步时,原始DDA计算的该正八边形块体最大、最小主应变分别 3.32×10-5及-2.60×10-5,此时四条对角线的线应变均未处于块体最大和最小主应变范围内的情况。这一现象随着计算时步的增大愈加明显。说明原始DDA在处理大转动问题时不仅会带来块体体积的自由膨胀,而且应变的直接叠加导致应变分量物理意义不明确,无法正确反映块体的实际变形。
3.2 矩形块体受均布荷载匀速旋转问题
如图6所示,以角速度ω= 0 .5π r ad/s 绕质心匀速旋转的等厚矩形薄板,长2L=6 m,宽2b=4 m。材料质量密度为ρ=2400kg/m3,弹性模量E=100 MPa,块体受大小为1 MPa的水平初始应力。采用一个块体模拟该矩形薄板的运动,假定块体不受重力作用,为消除应变对块体内应力场、速度场的影响,假定每时步内的应变分量增量

表2 原始DDA计算的主应变Table 2 Principal strains by original DDA
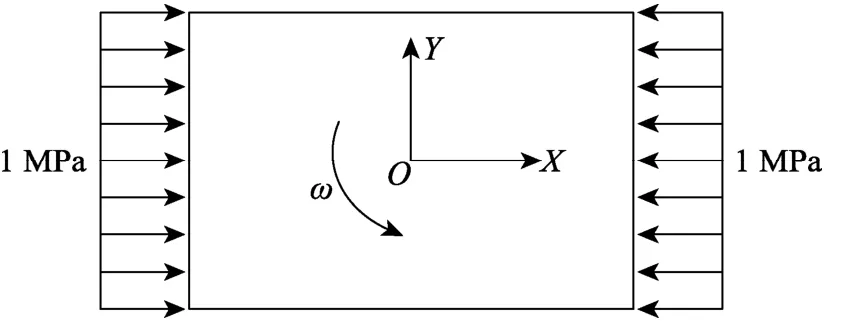
图6 矩形块体的几何形状及受力示意图Fig.6 Geometry and loading of the rectangular block

图7 原始DDA计算出的块体应力Fig.7 Stresses calculated by original DDA
取时间步长Δt=1 s,原始DDA计算出的块体应力如图7。由图7可见,块体的水平应力、竖向应力及剪应力与旋转的累积角度无关。表明原始DDA在计算转动块体时,计算出的错误应力方向直接影响块体内应力分布及弹性形变。
3.3 矩形块体绕质心匀速旋转问题
如图8所示为以角速度ω=0.2rad/s 绕质心匀速旋转的等厚度矩形薄板,长2L=6 m,宽2b=4 m。材料质量密度为ρ=2800kg/m3,弹性模量为E=2 GPa。为方便起见,假定矩形薄板处于平面应力状态,泊松比μ=0。以薄板质心为坐标原点O,如图示建立坐标系XOY。矩形薄板内任意点的正应变分量为:
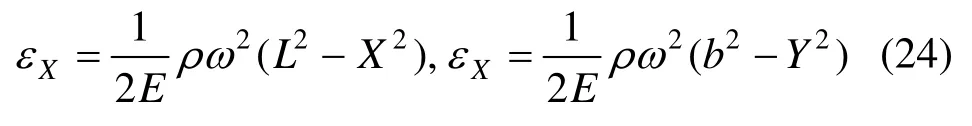
定义薄板平均正应变为:
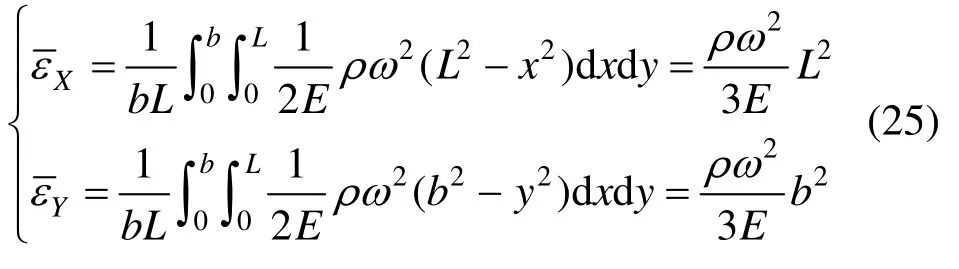

图8 绕质心匀速旋转矩形块体Fig.8 A rectangular block rotateing uniformly around the gravity center
采用一个块体模拟该矩形薄板的运动。图9给出时间步长 Δt= 0 .002s 时,原始 DDA及式(25)计算出的应变。

图9 不同方法应变对比Fig.9 Strains calculated by different methods
由图9可见,原始DDA不能反映离心力作用下薄板的应变,不能计算出由式(25)给出的块体平均应变解析解,给出了错误的应变。
4 结论
原始DDA的位移增量公式由块体的平动、转动及变形直接叠加而得,并假定块体每时步的转角增量足够小,由此得到线性化后的位移增量公式及相应形函数矩阵。而当模拟的块体产生转动时,块体体积出现错误膨胀,且块体内应变(应力)场发生畸变,从而影响DDA的模拟准确性及精度。
通过对原始DDA的位移模式、构型更新方式等分析,并通过数值算例验证原始DDA方法存在如下不足:
(1) 位移增量的简单叠加仅适用小转动条件;
(2) 应变分量增量是相对当前时刻定义的,不同时步应变增量参照构型不同,简单的累加导致应变分量物理意义不明确;
(3) 位移增量求解采用线性化后的近似表达式,随着计算时步的增加,引起误差累积,导致块体出现体积自由膨胀;
(4) 块体加速度应是从线性化前的位移增量表达式导出后再线性化,采用线性化后的位移增量公式忽略了块体转动引起的离心力和科氏力作用。
