基于最近邻量化距离聚类的残差中心聚合图像表示

2020-03-13张琳娜梁列全郑心炜阚世超岑翼刚

数据采集与处理 2020年1期

张琳娜，梁列全，郑心炜，阚世超，岑翼刚

（1.贵州大学机械工程学院，贵阳，550025；2.广东财经大学信息学院，广州，510320；3.北京交通大学计算机与信息技术学院，北京，100044）

引言

图像表示[1]是图像处理中的一个核心的问题，在图像分类[2-3]、图像检索[4-7]、目标检测[8-9]和图像分割[10]等应用中都是必不可少的过程。近年来，对图像表示的研究工作大部分集中在深度学习领域，此类方法采用卷积神经网络（Convolutional neural network,CNN），通过学习不同的卷积核，对图像进行逐层卷积和池化，最终用一个固定长度的向量表示一幅图像。由于卷积核是通过学习得到，因而基于CNN对图像进行表示在图像的大部分应用领域都取得了比基于传统方法对图像进行表示更好的效果。但是实验证明，大部分传统方法，如词袋模型（Bag of visual words，BoVW)[11]、聚合局部描述子向量（Vector of locally aggregated descriptors，VLAD)[1]、颜色统计等对图像表示的特征与基于CNN对图像表示的特征融合相比一般都具有互补性。因此，对利用传统方法进行图像表示的研究依然有必要。

主流的传统方法有基于颜色特征的图像表示和基于梯度特征的图像表示两种。在基于颜色特征的图像表示中，HSV颜色直方图[5]和CN特征[12]是应用最广泛的2种表示方法；在基于梯度特征的图像表示中，HoG梯度直方图，以及基于SIFT局部描述子[13]和SURF局部描述子[14]的BoVW和VLAD是应用最广泛的3种表示方法。本文主要基于SURF局部描述子，对VLAD方法进行改进，使其对图像表示的向量在图像检索等应用中能获得更加鲁棒的性能。

SURF描述子是基于SIFT描述子进行改进后提出的，SIFT描述子的建立过程有尺度空间生成和极值检测、关键点精确定位、关键点主方向确认和关键点描述子生成4个阶段，其在尺度空间生成过程阶段使用的是高斯滤波器，而SURF描述子在尺度空间生成阶段使用的是变换尺度的窗口滤波器，并且使用积分图降低计算量。两者相比，在限定所提取局部描述子的数量近似的情况下，SURF描述子的提取速度更快，且以更低的维度（SIFT通常是128维，SURF通常是64维）得到鲁棒性一致的图像表示。

在基于局部描述子进行图像表示的方法中，BoVW最早被提出，其主要思想是通过聚类一个较大的码本，并统计通过最近邻方法量化到码本上的每个码字中的描述子数量，得到统计直方图作为图像表示的向量。由于该方法仅仅统计了描述子数量，因而存在较大的信息损失，性能通常不理想。随后，VLAD和Fisher向量（Fisher vector,FV）[15]图像表示方法被提出来，VLAD的主要思想是通过聚类一个较小的码本（码字数量通常为64），然后累积通过最近邻方法量化到码本上的描述子与对应码字的残差和，最后级联每个码字对应的残差向量作为图像表示的向量。由于VLAD方法没有信息损失，因而在图像检索等应用中的性能远高于基于BoVW图像表示的方法。FV的主要思想是利用混合高斯模型训练码本，最终的图像表示由描述子的均值、标准差和混合高斯模型的权重系数决定。相对于VLAD模型，FV模型计算较为复杂，但是对图像表示的鲁棒性并不比VLAD模型更好。

VLAD模型的主要优点是计算简单、复杂度低，同时图像表示的鲁棒性好，因而被广泛使用。但是，当不同图像中的相同物体有多个重复或者相似的物体在不同图像中的大小不同时，所提取的SURF特征的数量通常差异比较大，在通过最近邻方式量化到码本上时，对于不同的相似图像，会造成同一个码字所对应的最近邻局部描述子数量差异较大，最终累积的残差和差异也较大。因而，在计算图像相似性时，会使得两幅相似的图像最终不相似。为此，本文主要针对该问题，提出一种最近邻量化距离聚类的残差中心聚合图像表示方法。

1 VLAD图像表示

1.1 VLAD图像表示的基本思想

给定一个有N幅图像的数据库D={Id}Nd=1，其中Id表示数据库D中的某一幅图像。假设从图像Id中提取的SURF描述子集合为表示从图像Id中提取的某个SURF描述子，n为描述子的数量。对数据库D中所有图像的SURF描述子聚类后得到码本中 ci为构成码本的码字，通常为聚类后的类别中心，k为聚类的类别数量，在VLAD图像表示模型中k通常为64。常用的VLAD图像表示为

式中

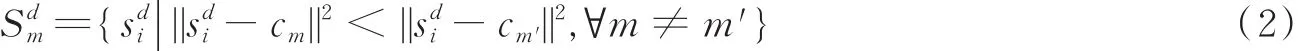
表示cm是的最近邻。

式（1）就是每幅图像的描述子对应每个视觉单词的累积残差和，级联所有，一幅图像就得到一个表示向量f通过二范数归一化后就得到图像Id最后的VLAD向量

1.2 VLAD图像表示的分析

从计算速度方面来看，式（1）中VLAD图像表示的计算过程主要是计算描述子的最近邻码字以及残差累积的过程，其中最占用时间的部分是计算描述子的最近邻码字。由于码字的数量通常为64，因而遍历码本的时间几乎可以忽略。因此该方法对图像表示的速度仅受描述子数量的影响。

从信息损失方面来看，该方法对残差进行累加求和，整个过程中没有信息损失，因此能用最终的向量保存一幅图像所有描述子的信息。

但是，具有相似结构的图像仅仅只是相似结构的数量不同，则会因为描述子数量的多少不一致而造成最终的累积残差不一致，进而导致两幅相似图像的表示出现较大差异。从式（1）来看，如果多个描述子与对应的最近邻码字的残差一样，则最终的残差累积和会因为描述子数量的不同而有较大差异。图1展示的是不同的相似图像SURF特征分布的可视化，矩形框中是3幅相似图像中具有相同内容的部分，由于距离和角度的不一致，第3幅图像在该部分的SURF特征数量明显少于前两幅。这种情况并不是特例，大部分图像由于内容的缩放和重复等都具有类似的情况。为处理该问题并获得更加鲁棒的图像表示，文本提出最近邻量化距离聚类的残差中心聚合图像表示方法。

图1 不同的相似图像SURF特征分布的可视化Fig.1 Visualization of SURF feature distribution for different similar images

2 最近邻量化距离聚类的残差中心聚合图像表示

2.1 基本思想

与VLAD方法类似，首先提取数据库中所有图像的SURF描述子，然后使用K均值聚类算法利用提取的所有SURF描述子聚类码本针对描述子，求解该描述子与其在码本C中的最近邻码字的欧式距离，表达式为

再次利用K均值聚类算法对基于式（3）求得的所有描述子对应的欧式距离聚类，得到聚类中心集式（3）求得的距离可以根据最近邻规则量化到集合上，表示如下

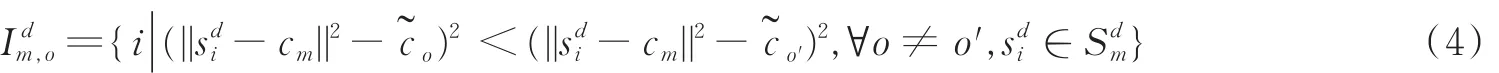
最后，对于图像Id，本文提出的图像表示思想如下：首先，根据式（3）求出描述子集合Sd在码本C中与其对应的最近邻码字的欧式距离集合Ed；然后，利用式（4）求出该距离集合中的样本在集合～C的最近邻索引。再次，求解对应的SURF描述子在码本C中与其对应最近邻码字的残差的均值，表达式为

与VLAD方法的后处理类似，级联所有crdm，1幅图像就得到1个表示向量f通过二范数归一化后就得到图像Id最后的表示向量fcd=fcd/||fcd||。

2.2 算法分析

VLAD方法在量化时仅在一个码本上进行索引，而本文提出的残差中心聚合量化使用两个码本进行量化。如图2所示，本文提出的方法在两个维度上进行索引。假设码本C中仅有10个码字（图2中水平方向），集合中仅有8个数字（图2中垂直方向），则本文方法首先在水平方向上找到最近的一个码字（假设为c6），然后求出描述子和该码字的最近邻距离，再次找到该距离在集合中最近的元素（假设为～c3），则该描述子对应的索引坐标就是(6,3)。

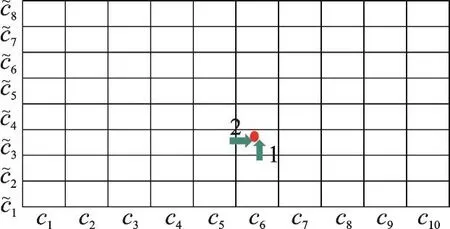
图2 SURF特征量化示意图Fig.2 SURF feature quantization example

将一幅图像中所有索引到坐标(6,3)的描述子与码字c6求残差，然后再求残差的均值即得到坐标(6,3)处的残差中心。将所有c6这一列的残差中心加起来就得到码字c6对应的残差中心聚集结果，其余码字也类似。最后依次级联所有码字对应的聚集后的残差中心就得到图像的表示向量。

二维量化的好处是对一维量化后的描述子按照距离进行归类，找出类别的中心进行聚集，该方法通过在二维空间进行聚类，进一步解决了因为描述子数量的不同而造成残差累积和有较大差异的问题，在实际图像表示中鲁棒性比VLAD方法更好。

如图3的例子所示，假设图像A中有20个相同的SURF描述子，与图像A相似的图像B中仅有2个相同的SURF描述子，这些描述子都同时量化到坐标(c6,～c3)处。在VLAD表示方法中，图像A中相似的描述子数量多，造成的累积残差大，图像B中相似的描述子数量少，造成的累积残差小，因而利用最后得到的图像表示会造成这两幅相似的图像不匹配。

通过本文方法，图像A中的描述子与码字c6求残差后再求均值，图像B中的描述子也与码字c6求残差后再求均值，最终得到的图像表示向量不会因相似描述子数量的不同造成差异较大的现象，因而，能获得更好的图像的表示向量。

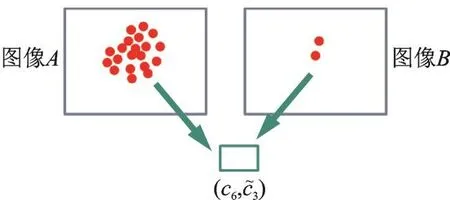
图3 距离聚类对残差累积和影响示意图Fig.3 Descriptor quantization example

2.3 图像表示复杂度分析

基于VLAD的图像表示方法仅仅只在码本C∈Rk×k中进行量化操作，其中k为描述子的维度，因此时间复杂度为O(k×k)。本文提出的方法在VLAD的基础上，还需要在码本～C∈Rl上进行量化，因此时间复杂度为O(k×k)+O(l)，由于l比k×k小得多，因此所增加的时间复杂度很小。

2.4 码本聚类方法

数据较少的聚类可直接采用K-means方法进行聚类。由于图像的局部特征较多，一个图像数据库中图像局部特征可能多达百万甚至十亿规模，使用K均值聚类会非常耗时，同时占用内存很高。此处本文采用Kan等[5]提出的两步聚类算法进行码本的聚类。假设最终要聚类的类别为K，则两步聚类算法简单归纳为：（1）将待聚类数据集平均分为R等分，并将每一等份用K均值聚类算法聚为类，其中X为一个大于等于2的常数，K为最终需要聚的类别向上取整符号。取出每一类的类中心组成新的数据集。（2）将第(1)步中聚类后的类中心集合用K均值聚类算法直接聚为K类即可得到最终的码本。由于该方法通过降低数据集的规模来实现聚类，因此能极大地降低聚类的复杂度，加快聚类速度。

2.5 特征降维和归一化

在图像检索中，首先提取图像的SURF描述子，然后用本文基于聚类得到的码本对SURF描述子进行编码后得到图像表示向量。由于SURF描述子的大小为64，码本中码字的个数也为64，因此1幅图像会被表示为1个4 096维的向量，在基于欧式距离进行相似性计算的图像检索中，由于维度太高，不仅速度慢，而且精度也不一定理想。因此，本文考虑使用主成分分析方法（Principal component analysis，PCA）进行降维，并利用特征值和特征向量做归一化处理。处理方法如下：

（1）将图像表示后的向量进行指数归一化，表达式为

式中：sgn(·)为符号函数，值大于0就为 1，小于 0为-1；abs(·)为取绝对值函数；⊙ 表示元素对元素的点乘；α为指数归一化中的指数系数，在实验中改值为设置为0.1。

（2）指数归一化后再次利用二范数进行归一化，表达式为

（3）通过PCA对所有图像的表示向量进行分解，得到分解后按照从大到小的顺序排列的特征值{l1,l2,…,ll}和对应的特征向量{m1,m2,…,ml}，其中l为降维后特征的维度，在实验中分别被设置为64,128,256和512。

（4）利用特征值和特征向量进行降维和归一化处理，表达式为

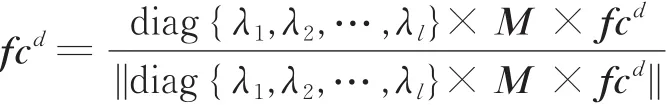
式中：diag(·)为对角矩阵，M为特征向量构成的矩阵。

（5）最后再次对将维并归一化后的向量利用二范数进行归一化fcd=fcd/||fcd||。

通过以上步骤处理后，图像表示特征的维度可以被大大降低，同时还能一定程度上增强特征匹配的鲁棒性。

3 图像检索实验与结果分析

3.1 实验数据集和评价标准

本文实验的数据集为Holidays数据集[16]和UKB数据集[17]。Holidays数据集共有1 491张高分辨图像，其中有500张查询图像。该数据集是相似图像检索的公共数据集，并且被普遍用来评价相似图像检索算法的性能。UKB数据集共有10 200张图像，总共包含2 550类，每类4张图像，在检索时，每1张图像都被用于查询图像检索1次。该数据集也被广泛用于评价相似图像检索算法的性能。

本文在Holidays数据集上使用平均类别的平均准确率[18]（mean Average precision,mAP）作为评价指标，AP的计算公式如下

式中：i为检索结果的排序位置；P(i)为前i个结果的准确率；B(i)为第i个结果是否与查询图像的真实结果相匹配，若匹配则为1，不匹配则为0；NG为查询图像对应的真实结果的数量。mAP就是所有查询图像AP的平均值，表达式为

式中Q为查询图像的数量。

在UKB数据集上，本文使用N-S得分作为评价标准，在该数据集上通常使用该标准作为检索结果的评价标准。该数据集上N-S得分的计算如下

式中：P(q)为查询图像返回结果排序中前4个结果的准确率；Q为查询图像的数量。

3.2 Holidays数据集上的实验

首先，提取Holidays数据集上的SURF描述子，为了能快速聚类码本，本文使用Kan等提出的两步聚类算法聚类大小为64的码本，在两步聚类算法中：第1步对每1张图像的SURF描述子聚类，聚为20类；第2步将第1步聚类的结果直接聚为64类就得到最终的码本大小。

然后，根据式（3）计算SURF描述子与码本中对应最近邻码字的欧式距离，并用两步聚类算法进行聚类。此处，为了观察不同类别数目对算法性能的影响，在两步聚类算法的第2步分别设置聚类数目为：64，128，256，512和 1 024。

最后，根据式（4—6）进行图像表示，并用主成分分析方法（Principal component analysis，PCA）分别降维到64，128，256和512维，降维前后的图像检索mAP随距离聚类数目变化的曲线如图4所示。图4中横坐标是特征的维度，4 096表示没有PCA降维，64，128，256和512是使用PCA降维后的维度，纵坐标是在该数据集上检索的mAP值。图例中VLAD表示特征使用的是VLAD图像表示方法，“Our-”方法表示本文提出的方法，数字 64，128，256，512和 1 024表示聚类距离时的类别数目。

从图4可以看出，在使用PCA降维时，本文提出的方法在维度降到128维时效果最好，而VLAD方法在维度降低到256维时效果最好。在该数据集上，使用PCA将特征维度降低到64，128和256维时，效果都比使用没有降维时的特征检索的结果好。同时，本文方法在距离聚类数目为512和1 024时，检索结果比VLAD方法得到的检索结果好。上述结果验证了本文提出方法的有效性。

需要注意的是，当距离聚类的数目为64时，本文方法得到的检索mAP没有VLAD方法好，说明距离聚类时类别数目不能太小，否则会造成信息的损失，影响检索精度。同时，如果距离聚类的数目无限接近总的描述子数量，本文方法得到的图像表示结果将无限接近于VLAD图像表示的结果。因此，本文方法需要设置合适的距离聚类数目。

通过该实验可以得出，综合考虑时间和效率，距离聚类数目设置为512或1 024比较合理。如果距离聚类数目太大，图像表示时增加的时间更多；如果距离聚类数目太小，图像表示时准确率未必会比VLAD更好，或者准确率提升不明显。

需要注意的是，在该数据集上PCA降维后图像检索的准确率增加了，特别是维度降低到128维时准确率增加得比较明显。这是因为：一方面本文基于欧式距离来计算两幅图像之间的相似性，而欧式距离对高维数据并不鲁棒；另一方面该数据集通过基于码本的方法进行图像表示后信息有冗余，通过PCA降维后能减少冗余信息，进而提高准确率。

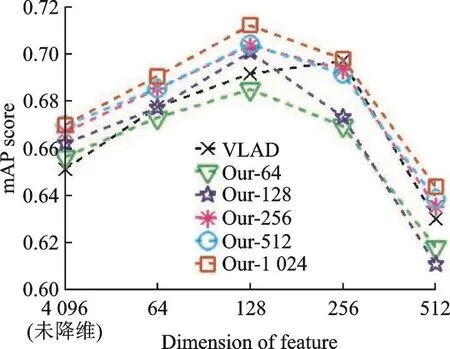
图4 Holidays数据集上的检索结果Fig.4 Retrieval results on Holidays dataset

3.3 UKB数据集上的实验

与Holidays数据集类似，首先提取UKB数据集中每一幅图像的SURF描述子，并使用两步聚类算法聚类大小为64的码本。然后对根据式（3）计算的SURF描述子与码本中对应最近邻码字的欧式距离，并用两步聚类算法分别聚类为：64，128，256，512和1 024类。最后根据式（4—6）进行图像表示，用PCA方法对表示结果分别降维到64，128，256和512维进行图像检索，降维前后的图像检索N-S得分随距离聚类数目变化的曲线如图5所示。

从图5可以看出，在PCA降维后该数据集上各种特征的检索精度都降低了。同时，本文方法的检索结果在距离聚类数目为512和1 024时略比VLAD方法效果好。该数据集上本文方法效果表现没有Holidays数据集的效果明显，主要原因是该数据集每1类图像仅有1个目标，并且仅有旋转的不同，图像中没有重复的目标，也没有缩放现象，因此相同类别的图像特征数量基本一致，本文方法在该数据集上的表现与VLAD方法类似。

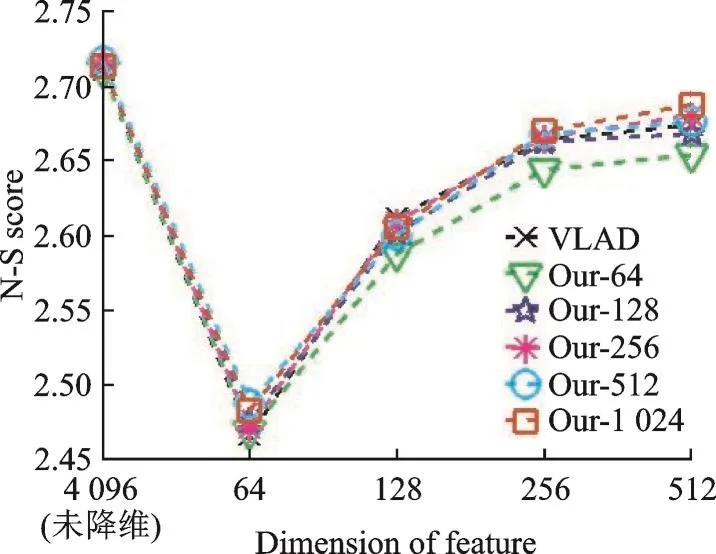
图5 UKB数据集上的检索结果Fig.5 Retrieval results on UKB dataset

3.4 性能比较

由于本文方法是改进的VLAD图像表示方法，因此实验中将本文方法与VLAD方法以及相关的VLAD改进方法进行对比。在Holidays和UKB数据集上的对比结果分别如表1和表2所示。

从表1中可以看出，在Holidays数据集上，对于4 096/8 192维（基于VLAD方法为4 096维，基于SIFT方法为8 192维）和128维的图像表示向量，使用本文方法（Our-1 024），mAP比VLAD方法分别提升1.88%和2.04%，比Wang等改进后的加权VLAD方法分别提升1.06%和1.30%。同时，在PCA降维后，图像检索准确率进一步增强，表1中第2行VLAD方法在降维后的检索结果是根据本文2.3节的流程降维后的检索结果。

从表2中可以看出，在UKB数据集上，对于4 096维的图像表示向量，本文提出的方法获得了最好的结果，N-S得分分别比VLAD方法和加权的VLAD方法高0.006 4和0.000 8。

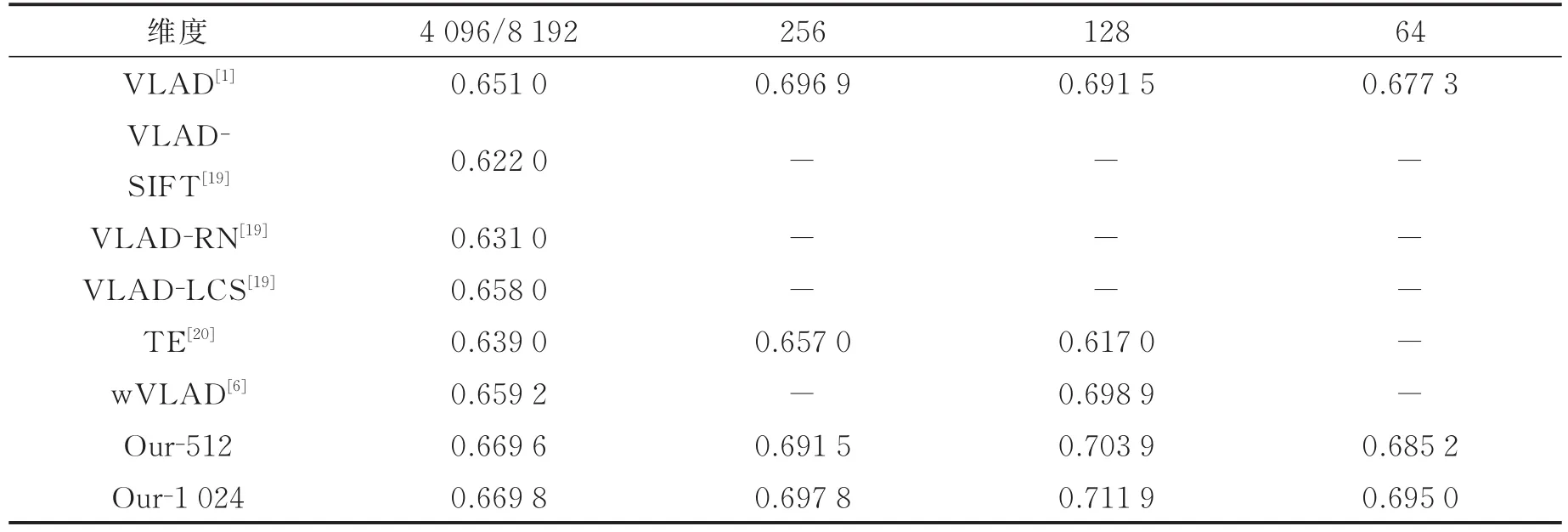
表1 Holdiays数据集上的检索结果对比Table 1 Comparison of retrieval results on the Holdiays dataset

表2 UKB数据集上的检索结果对比Table 2 Comparison of retrieval results on the UKB dataset

此外，为了对比观察不同方法的检索结果，给出VLAD方法和本文方法在Holidays和UKB数据集上的部分检索结果案例，如图6，7所示。图6中第1列为查询图像，前3行是4 096维图像表示特征给出的查询结果排序，后3行是128维图像表示特征给出的查询结果排序。红色框中的图像表示与该查询图像真实匹配的结果。从查询结果中可以看到，本文方法（Our-1 024）在PCA降维到128维后获得了最好的查询结果。