大规模MIMO预编码码本的优化设计与分析*

安国刚，金红军

（1.杭州电子科技大学 电子信息学院，浙江 杭州 310018；2.中国电子科技集团第五十研究所，上海 200000）

0 引 言

近几年，无线通信技术讯速发展，尤其是4G技术的普及应用，系统的传输速率和用户体验得到极大提高，进一步刺激了人们对无线业务的需求，使人们对移动宽带接入﹑大数据承载﹑服务体验等方面提出了更高要求[1]。可以预见，未来网络数据流量将呈现成百上千倍增长的井喷态势。因此，下一代5G技术更成为学界研究的热点。其中，大规模MIMO技术可以获取更高的链路可靠性和数据传输速率，已成为国内外研究的热点[2]。

大规模MIMO技术与多用户相结合形成的大规模多用户MIMO（Multiuser MIMO， MU-MIMO）系统，可进一步利用空间自由度大幅提升系统的吞吐量和频谱效率[2]。预编码作为MIMO系统的关键技术，可有效抑制多用户干扰和提高接收信噪比[3]。然而，要充分发挥预编码作用，发射端必须获得足够的信道状态信息（Channel State Information，CSI）。对于时分双工（Time Division Duplex，TDD）系统，可通过上下行信道的互易性得到CSI，但易受导频污染[4]的影响。在频分双工（Frequency Division Duplex，FDD）系统中，CSI的获取主要依靠反馈链路，而实际系统中 反馈链路带宽有限。因此，在FDD大规模MIMO系统中，通常采用基于码本的多用户预编码方案，其中码本设计和反馈开销尤为重要。

1 系统模型

对于频分双工FDD系统，通过UE（客户端）对信道进行估计并得到结果，即CSI反馈给BS，BS使用该信道状态信息进行波束成形。

多用户MIMO系统如图1所示。考虑单个小区场景，小区基站采用N×1维均匀线性阵列天线，用户采用单天线，小区内用户总数为N，基站同时调度的用户数为K。在下行FDD大规模MIMO系统中，用户根据接收到的导频信号估计出CSI，再根据CSI确定最优的预编码矩阵索引（Precoding Matrix Index，PMI）和相应的信道质量指示（Channel Quality Indication，CQI），并通过有限反馈链路将其反馈至基站，从而实现闭环预编码。

图1 大规模MIMO预编码系统

假设用户获得相同的功率分配，则第k个用户接收到的信号可表示为：

其中Hk∈C1*N为基站到第k个用户的信道矩阵；Fi∈CN*1为第k个用户的预编码矩阵；sk∈C为基站发送给第k个用户的数据符号，且满足E{si*si}=1，即总发送功率为k，nk∈C表示均值为0﹑方差为σ2的复高斯白噪声，即nk～CN(0,1)。式（1）中，HkFksk为每个用户的有用用户间干扰项，nk为白噪声项。

2 码本设计

2.1 DFT码本设计

基于DFT（Discrete Fourier Transform，DFT）矩阵的码本是一种经典的码本设计方案，实现起来简单易行。相关性较强信道的情况下，有较好的预编码性能，且其可以较好地实现波束赋形，也具有恒模和限定字符集特征，同时存储和搜索开销较小。若发送天线数目为Ntx-1，W为预编码矩阵，wm-1为矩阵W的第m个预编码向量，则预编码矩阵构造如下：

其中L的大小决定满秩情况下的码本大小。比如，当发送天线Ntx=4﹑L=2时，其预编码码本大小为2，码本包括如下两个预编码矩阵，即：

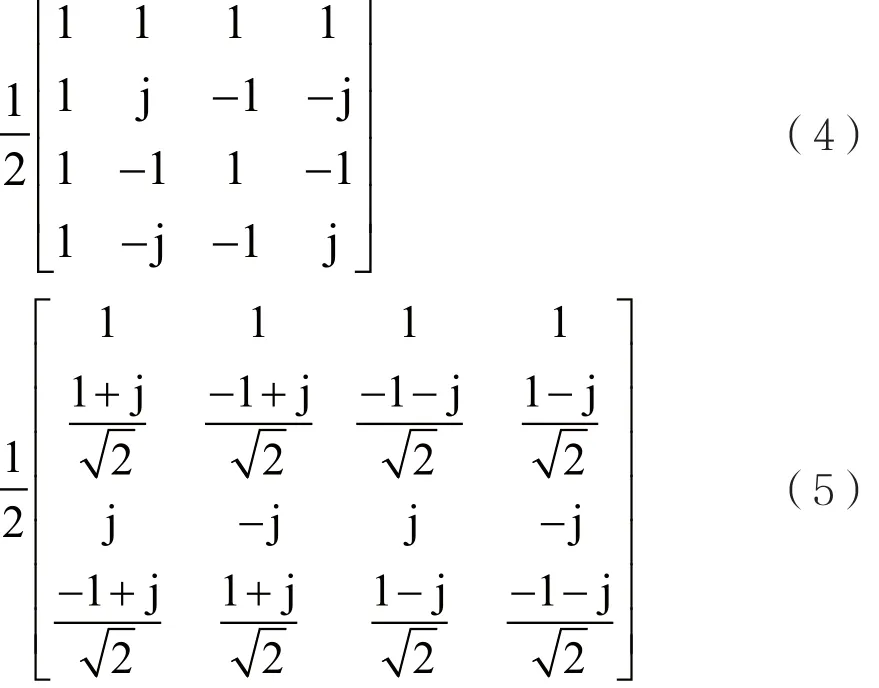
2.2 Grassmannian码本设计

基于Grassmannian码本的设计，可以描述成Grassmannian子空间封装问题[5-7]。在信道独立同分布情况下，Grassmannian码本构造方案是最可能获取最优功能的方案。Grassmannian子空间封装中的性能测度是弦距离，被定义为：

图2 预编码矩阵和弦距离

对于任意的天线数Ntx﹑码字长度M和码本大小L，求解Grassmannian子空间封装问题需要耗费大量时间，且无法直接得到[6-8]。因此，需要考虑一种次优但更加实际的设计方案。一种特定的方法就是使用文献[9]给出的码本矩阵：

从Ntx×Ntx的码本矩阵中选择M列得到一个码字W，其中码本矩阵的(k,l )元素k,l=1,2,…,Ntx。此外，θ是对角矩阵：

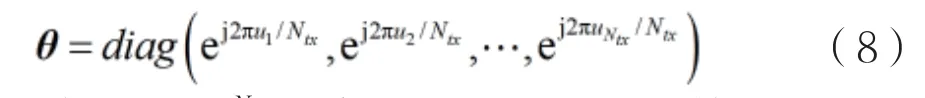
在IEEE802.16e标准中，不同的Ntx﹑M和L的情况，u=[u1,u2,…uNtx]的取值不同。例如，当Ntx=4，M=3，L=64时，有：

由式（11）得到剩余的预编码矩阵Wi：

其中i=2,3,…,64。

3 改进码本设计

以上两种码本设计方案是在发送端和接收端设计相同的码本集合，然后用户根据接收到的导频信号估计出CSI，再根据CSI确定最优的预编码矩阵索引PMI和相应的信道质量指示CQI，并通过有限反馈链路将其反馈至基站，从而实现闭环预编码。改进码本设计方案是在DFT码本的基础上，根据反馈回来的PMI先从发射端码本集合中选中目标码本，再结合Grassmannian码本以这个目标码本为中心，创建一个码本间量化距离比原来更小的码本集合，再重新搜索一遍得到最优码本。

具体实现方法如下。分析DFT码本设计式（3）可知，DFT码本是一种离散化码本，结合Grassmannian码本思想，离散化码本之间距离，分析DFT公式可知，码本向量与相邻码本向量之间是根据1/L值的大小发生变化的，Grassmannian码本通过给定一个码字，再通过将θi（i=1,2,…,L-1）与W1相乘得到剩余的L-1个码字。通过最大化最小弦距离来确定码本集合，这样需要计算任意两个码本之间的弦距离，计算量很大。由于DFT码本向量之间是根据1/L值的大小发生变化的，则不用计算最大化最小弦距离来确定码本集合，只需将式（8）变为式（12）即可：

这样不用计算最大化最小弦距离，因为本身DFT码本的设计方法就是离散化的，所以根据DFT码本的设计公式可仿照出θ对角矩阵，然后通过θW1来确定下一个码本，通过改变1/L来改变码本向量之间的弦距离。

例如，M=4，L=2的两个DFT码本可以确定第一个码本W1，然后令：

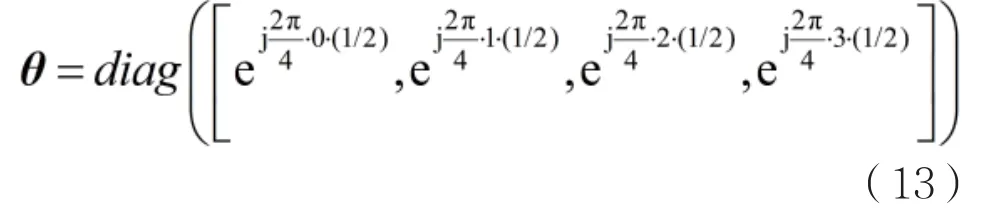
通过θW1可以得到W2，还可以改变1/L的值来增加码本。例如，令L=4，则令W3=θW1，则相当于在W1和W2之又增加了一个码本W3，继续增加L改变1/L，还可以继续增加码本。

4 仿真分析

对有限反馈多用户MIMO下行链路误码率进行理论仿真及分析。系统参数设置：基站采用线性阵列模型，天线间隔d=λ/2，其中λ为载波波长，小区内有10个候选用户，调度用户数K=2，采用DFT码本以及本文设计的码本方法，在不同反馈量以及在不同方法下对误码率进行实验与分析。

图3给出了采用DFT码本方法进行预编码时，误码率随着信噪比的变化曲线。由仿真曲线图可以看出，随着信噪比的增加，误码率越来越小。随着码本反馈量的增加，误码率性能变得越来越好。这是因为DFT码本对于采用均匀线性阵列的无线信道有较高的适配性，码本集合中每一个码本矢量对应着一个量化角度信息，同时相邻的码本矢量又具有一定的角度间隔，并在整个圆周[0,2π]上分布。随着码本数量的增加，相邻码本矢量的量化角度间隔变得越来越小，这样在通信过程中能够得到更加准确的CSI，所以曲线误码率性能会越来越好。

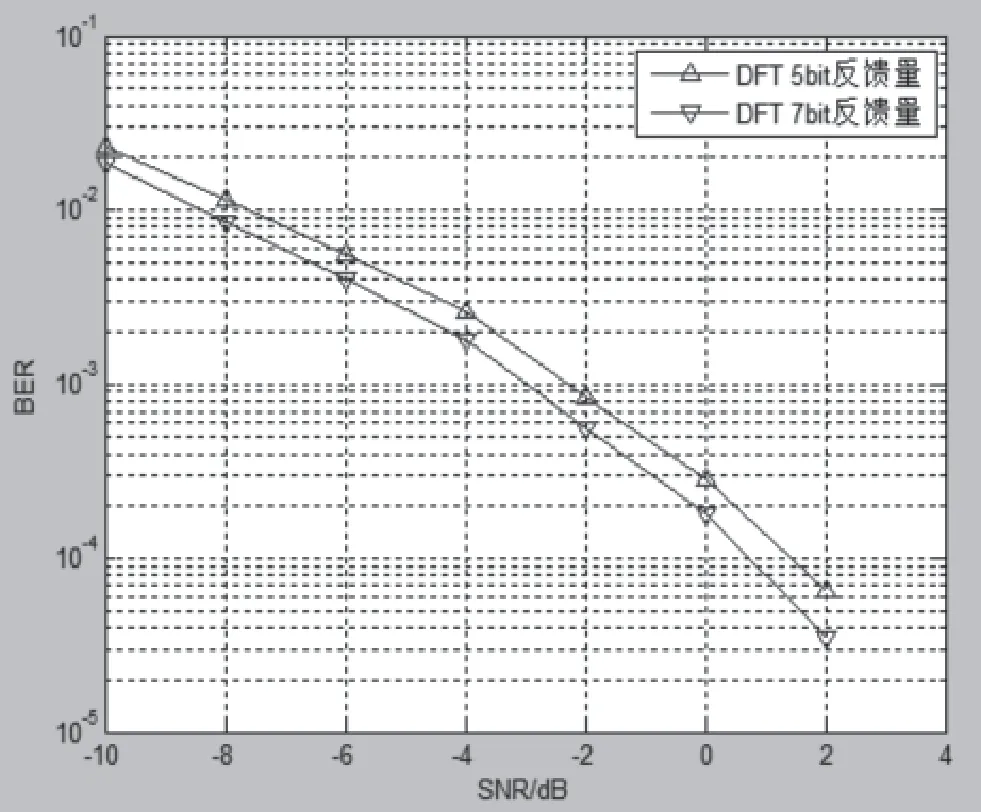
图3 基于DFT码本的预编码误码率曲线

图4给出了采用DFT码本与改进码本时，误码率随着信噪比的变化曲线。从仿真曲线图可以看出，随着信噪比的增加，两种码本方法的曲线误码率都变得越来越小。但是，对于同一反馈比特量，改进码本的误码率性能要好于DFT码本的误码率性能。此外，改进码本的反馈为5 bit与DFT码本的反馈7 bit的误码率性能相当。这是因为改进码本在反馈到发射端后还要进行一次码本集合的创建与搜索，而改进码本集合的创建与搜索就是为了使目标码本矢量与周围码本矢量的量化角度间隔变得越来越小，从而获得更加准确的CSI。所以，曲线的误码率性能会变得越来越好。

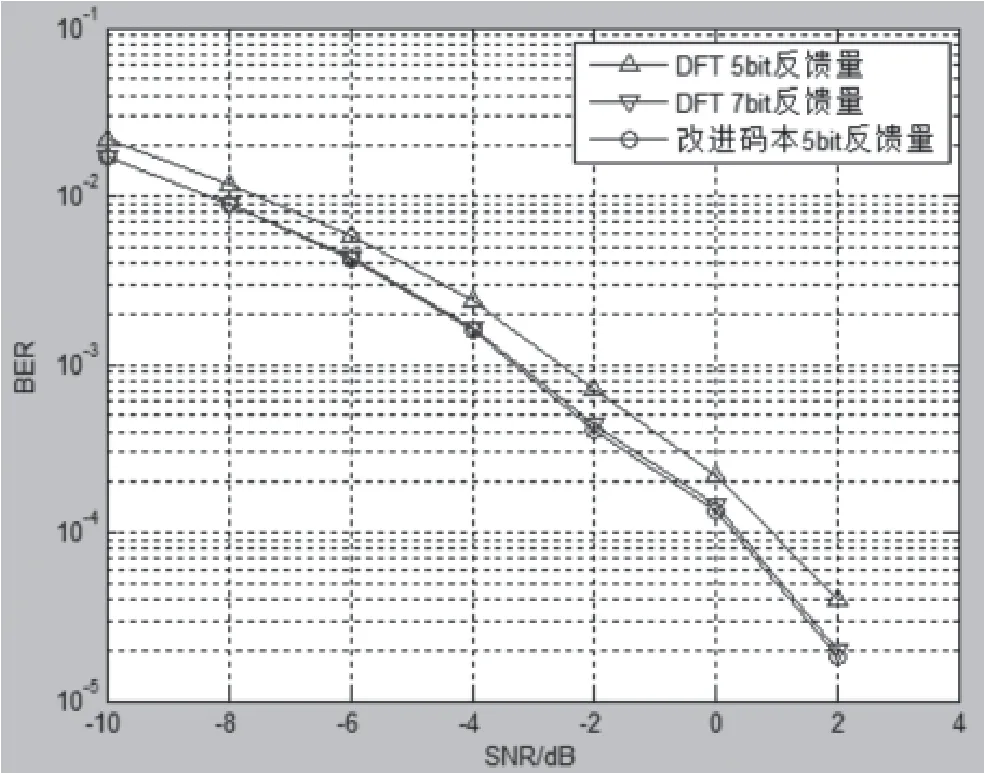
图4 改进码本和DFT码本的预编码误码率曲线

5 结 语

在研究DFT与Grassmannian码本方法的基础上，本文提出了一种新的码本设计方案，并从理论上分析了这种方法的可靠性和正确性，同时通过实验模型进行了仿真。仿真结果表明，新型码本方法在相同反馈链路开销情况下，比DFT码本方法具有更好的误码率性能，有效改善了系统误码率，对有限反馈无线通信系统实际应用与推广具有一定的理论和工程应用价值。

[1] XIA P,GIANNAKIS G B.Design and Analysis of Transmitbeam Forming based on Limited-rate Feedback[J].IEEE Trans. Signal Processing,2006,54(05):1853-1863.

[2] WANG Ming-hui,JIN Hong-jun,WANG Wen-yong.Analysis and Comparison of Different Precoding Algorithms for Downlink Massive MIMO Systems[J].Communications Technology,2016,49(09):1134-1138.

[3] HANG J,SHE F.Capacity and QoS Based Codebook Construction for MIMO Precoded Spatial Multiplexing Systems with Limited Feedback[J].Journal of Shanghai Jiaotong University,2009,14(02):215-218.

[4] ZHOU S L.BER Criterion and Codebook Construction for Finite-rate Precoded Spatial Multiplexing with Linear Receiver[J].IEEE Trans. Signal processing,2006,54(05):1653-1665.

[5] Love D J,Heath R W.Limited Feedback Unitary Precoding for Orthogonal Space-time Block Codes[J].IEEE Trans. Signal. Proc.,2005,53(01):64-73.

[6] Conway J H,Hardin R H,Sloane N J A.Packing Lines,Planes,etc.:Packings in Grassmannian Spaces[J].Experimental Math,1996(05):139-159.

[7] Barg A,Nogin D Y.Bounds on Packings of Spheres in the Grassmann Manifold[J].IEEE Trans. Info.Theory,2002,48(09):2450-2454.

[8] Strohmer T,Heath R W.Grassmannian Frames with Applications to Coding and Communications[J]. Appl. Comput.Harmon. Anal.,2003(14):257-275.

[9] Hochwald B M,Marzetta T L,Richardson T J,et al.Systematic Design of Unitary Space-time Constellations[J].IEEE Trans. Info. Theory,2000(46):1962-1973.