降维突破思维难点，升维发展空间观念

2020-03-10徐磊

广西教育·A版 2020年12期

徐磊

【摘要】本文以《正方体的表面展开图》教学为例，论述帮助学生突破学习几何知识难点、发展空间思维的方法，建议教师通过“体—面—体”的有效转化，用“降维”的方式让三维立体图“躺”下来，初步建立面体之间的联系，再“升维”将二维平面图“立”起来进一步认识，从而勾连学生对二维平面图和三维立体图之间的联系，发展学生的空间观念。

【关键词】小学数学几何思维空间观念

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2020）45-0108-03

小学生的几何思维具有具体性和抽象性相结合的特点，受限于自身抽象思维的发展，他们学习的几何知识更多的是经验几何，而不是严格的以逻辑推理为公理化的体系。六年级的学生初次接触抽象的三维立体图形，缺少具体直观的经验，所以在认识和理解上往往存在很大的困难。如何帮助学生突破学习几何知识的难点，更好地发展空间观念呢？通过教学《正方体的表面展开图》，笔者有了一些自己的思考与认识。

我们通过认真观察可以发现，把立体图形的表面展开后会有以下变化：原来存在于三维空间的6个正方形被置放到了同一平面上。原来在立体图上最多只能同时看到3个面，而在表面展开图上能看到正方体的6个面，把抽象化为直观，能使正方体的特征表象更清晰，也便于学生解决一些问题。然而，这也给学生的认知带来一些困难，如学生原本能直觀感受到在正方体上3组相对面的位置关系，而表面展开图会因为展开的方式不同而发生变化，学生需要凭借折回的过程进行思考，这就要求学生具备一定的空间想象能力，增加了认知的难度。

在教学中，教师该如何帮助学生体会表面展开的价值，突破认知困难，发展空间观念呢？笔者认为应从“有效”入手，做细转化的过程，通过观察、操作、想象等手段丰富表象，发展学生的空间观念。具体做法如下：

一、让“维”降下来，激发探求内需

怎样引导学生产生把正方体的表面展开的需求呢？笔者创设了以下教学情境：

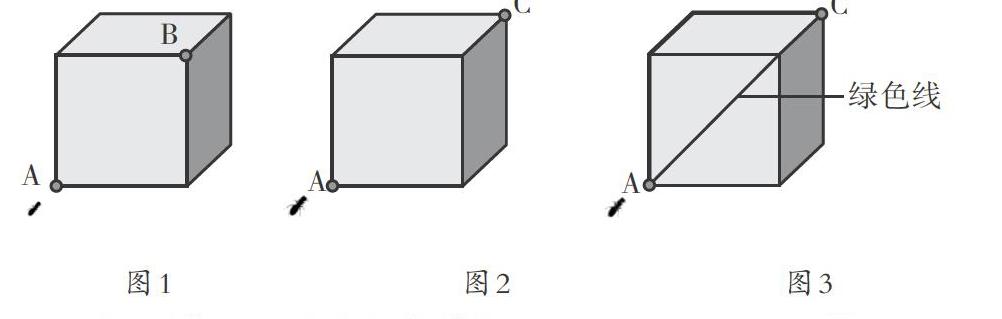
谈话：小蚂蚁带来了一个正方体。从A点到B点，怎么走最近？（如图1）你怎么想的？……是的，A、B两点都在一个面上，同一平面内，两点之间线段最短。

提问：如果从A点到C点，怎么走最近？（如图2）你怎么想的？（出示学生可能规则的路线，如图3）

图1 图2 图3

谈话：从正面的A点走到上面的C点，你们都觉得绿色的路线更近，那还有没有更近的？联系由A点到B点的最近路线，我们得到的结论，你有没有什么想法？同桌之间可以互相说一说。

提问：有没有同学有新的路线？你是怎么想的？

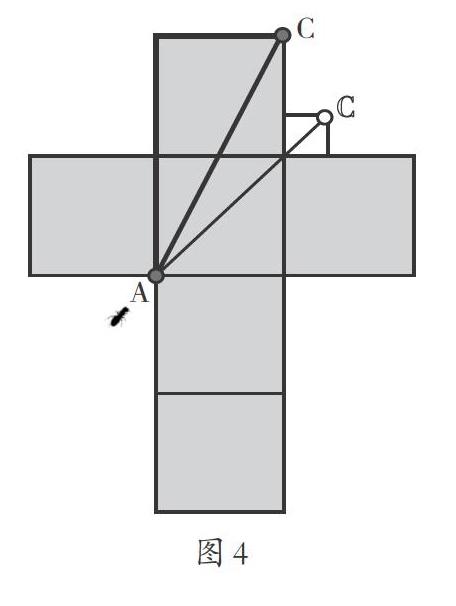
追问：他是怎么解决的？谁再来说一说。（媒体演示动态展开，如图4）

小结：在这个正方体上，A点和C点不在同一平面，如果把正方体的表面展开，这样A点和C点就在同一平面上了，问题就能解决了。

揭示概念，板示课题：像这样把正方体的六个面展开放在同一平面上，并且两两相连，得到的图形就是正方体的表面展开图。本节课我们来研究正方体的表面展开图。

从以往的教学中笔者发现，在二维图形中学生知道“两点之间线段最短”，而在三维立体图上寻找不同平面内的两点之间的最短线段，这个任务是学生根据已有经验无法解决的，他们大多是沿着正方体的棱寻找，或将相应平面内的最短线段相连。即使学生借助实物寻找，这对学生来说依然比较抽象，他们难以找到。设计“蚂蚁找最短路径”的情境导入，一方面是借助问题情境激活学生的已有经验，并制造新旧知识的冲突，学生会发现已有的知识经验无法解决现有的问题，继而自主产生学习新知的需求，从而调动学习的积极性。另一方面，通过展开正方体表面的“降维”过程，使学生发现可以将三维立体的复杂问题变成二维平面的简单问题，初步体会到三维和二维之间的联系，了解可以借助二维展开图进一步认识立体图形。

二、让“体”“躺”下来，建立面体联系

在认识正方体表面展开图的环节，教材设计了让学生沿指定路径剪开正方体纸盒的操作活动，旨在让学生经历“动手剪”的过程，进而认识正方体的表面展开图，但笔者觉得如果把教学目标仅仅停留在这一层次，不能很好地发展学生的空间观念。

怎样让“体”“躺”下来呢？根据小学生的几何思维特征，笔者认为应通过正方体“躺”下来的过程，请学生思考：剪开一个面最多需要剪开几条棱？同一个面，剪开的棱不同，展开的方式也会怎样？剪开不同的棱，可能会展开怎样的面？基于这样的思考，笔者细化了表面展开的过程：

（一）指导示范

谈话：正方体的表面怎么展开呢？（出示三视图，如图5）

1.如果要展开这个正方体的前面，想一想，需要剪开哪几条棱？（学生回答）

如果剪开了3条棱，这条黄色的棱（图6中的AB）还能剪吗？（如图6）为什么？

交流明确：展开这个面，最多只能剪开3条棱。

2.接着你想展开哪个面？（学生回答）

图5 图6

图7 图8

如果展开上面，要剪开哪几条棱？