类比探究方式教学

2020-03-10杨宋羽刘华

读书文摘（下半月） 2020年8期

杨宋羽刘华

摘要：“学而不思则罔，思而不学则殆”，这说明教师在教学活动中，指导学生“学会学习、学会思考”远比“学会知识”更重要。所以在教学过程中，教师应以学定教，为学而教。为达到有效教学，对于不同的知识进行教学时，采取恰当的教学方式就更为重要了。以初中数学教学内容为研究对象，做出一个用类比探究方式开展的教学实例，以期能体现出类比探究方式教学的重要性、有效性与可行性。

关键词：类比法;初中数学;不等关系

类比法是一种最古老的认知思维与推测方法，也是一种科学研究的方法，更是最重要的数学思想方法之一。在我们的初中数学类比法是极为常见的。纵观初中数学，许多概念具有相似的属性，许多题型具有类似的解题策略、解题方法，某些内容的呈现方式也类似，对于这些具有共同点的学习内容，教师可以根据学情运用类比的手段进行教学，有利于提高课堂效率，而学生借助类比法学习，能有效降低学生对理解新知的难度。教学的方法是多种多样的，本文根据“不等关系”一课为例，根据学生的学情，巧用类比法进行教学。

一、“类比法”驱动下的教学设计

1.创设实际情景，感受身边的不等关系

问题1 在日常生活中，我们经常会进行比较，比如比较身高、体重、大小……，比较的结果可概括为哪两种？

问题2 相等关系的量如何用数学语言表示？

问题3 在你身边还有哪些不等关系？

设计意图：通过生活中的“比较”，引出等量关系与不等关系，通过观察身边的数量关系，充分让学生感受生活中存在着大量的等量关系与不等关系，为后面与等量关系类比来学习不等关系做铺垫。

2.类比探究，获取新知

【活动探究一】初步尝试建立不等模型，认识不等式

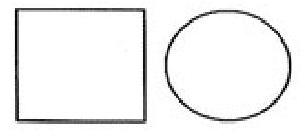
如图，用两根长度均为lcm的绳子分别围成一个正方形和一个圆。

问题1 如果要使正方形面积不大于25cm2，那么绳长l应满足怎样的关系式？

追问如果要使圆的面积不小于100cm2，那么绳长l应满足怎样的关系式？

问题2 当l=8时，正方形和圆的哪个大？l=12呢？

追问改变l的取值再试一试，由此你能得出什么猜想？

设计意图：从熟知的比较的正方形和圆的面积大小问题出发，有助于降低学生初次建立不等模型的难度。在探究同周长的正方形与圆的面积大小时，从对特殊的情况分析入手，再推广到一般情况得出结论，这个过程中给学生渗透“从特殊到一般”的数学思想。

【活动探究二】用不等式表示数学中的不等关系

问题1 如何用方程模型表示数学中的等量关系？

问题2 类比数学中的等量关系的表示方法，你认为如何表示用不等式表示数学中的不等关系？

问题3 用不等式表示数学中的不等关系的关键步骤是什么呢？

设计意图：以上的习题可以让学生进一步了解数学中的不等关系的呈现方式，感受到不等关系在数学中也是大量存在的，引起学生对不等关系的重视。通过类比分析利用数学中的等量关系建立方程模型的方法，引導学生找出不等式模型的建立方法的关键，即抓住不等关键词，将不同的不等关键词转化为数学符号语言，这里也强化了学生对转化思想的理解。

【探究活动三】用不等式表示实际问题中的不等关系

问题1 用方程模型表示实际问题中的等量关系关键是什么？

问题2 类比方程模型的建立过程，你认为建立不等式模型的关键步骤是什么？

问题3 对以上问题分析，说一说建立不等式模型的具体步骤。

设计意图：类比分析方程模型的建立过程，引导学生找到在实际问题中建立不等式模型的基本步骤，并能抓住建立不等式模型的关键环节，即抓住不等关键词进行分析。

3.融合应用

问题1 利用等量关系建立方程模型是为了求出具体的数量，那么不等式模型能求出具体的数量吗？

问题2 不等式模型不能求出确定的数量，那么研究不等式模型有何价值呢？

4.总结反思

（1）你学到了什么知识和思想方法？

（2）你还有哪些困惑？

设计意图：把课堂总结的主动权交给学生，有助于学生自主反思本节课中自己还存在着哪些困惑。教师要引导学生多思考知识点以外的学习收获，正所谓学知识，更要学方法，只有让学生掌握了方法，学生才能更好地利用所学知识去解决问题。