在变式教学中提升数学思维能力

浙江师范大学物理与电子信息工程学院 孔胜涛 321004

所谓“变式教学”这里是指在数学教学中通过对数学问题多角度、多层次的变换，突出数学问题的本质特征，引导学生从变的现象中发现不变的本质，从不变的本质中探索变的规律，目的在于培养学生灵活多变的数学思维能力.在高中数学解题教学中，如何才能有效提升学生的数学思维能力？这是值得每一位数学教师积极探索的问题.笔者拙见，在高中数学解题教学中，实施变式教学能有效提升学生的数学思维能力.但在实施变式教学时，切忌随意、盲目地进行变式，要结合教学内容和教学目标，适时适度地进行.下面以一道线性规划高考题的变式教学为例，介绍在高中数学解题教学中让学生的数学思维能力因实施“变式教学”而提升的一些思路和方法.

A.-1 B.1 C.10 D.12

解析：作出满足已知条件的可行域，如图1所示.

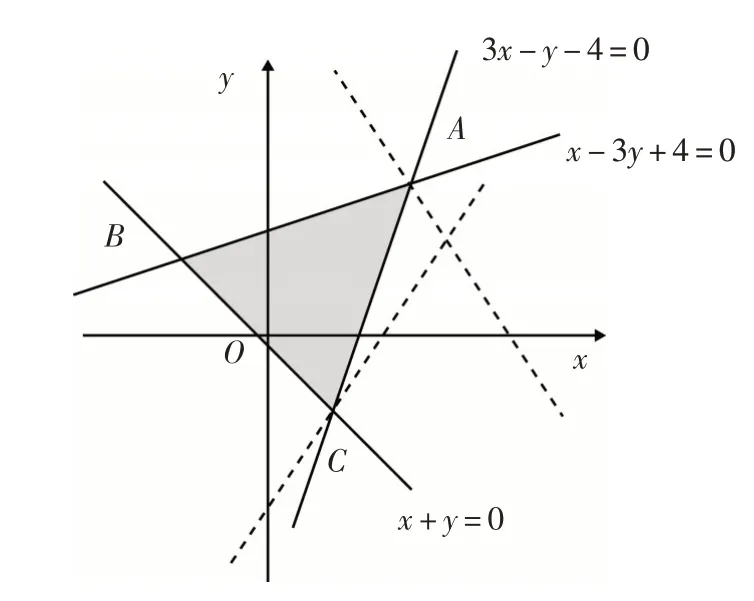
图1

解法2：（端点代入法）把A(2,2)，B(-1,1)，C(1,-1)代入z=3x+2y，得zmax=10.故选C.

1 改变目标函数

1.1 目标函数为线性目标函数

解析：作出满足已知条件的可行域，如图1所示.

解法2：（端点代入法）把A(2,2)，B(-1,1),C(1,-1)代入z=3x-2y，得zmax=5.

评注：对线性目标函数z=ax+by(b≠0)的最值问题，要注意b的正负性对z的影响.

1.2 目标函数为含参线性目标函数

解析：作出满足已知条件的可行域，如图1所示.

解法2：（端点代入法）把A(2,2)，B(-1,1),C(1,-1)代入目标函数z=ax+2y，可分别求得a=2，a=-6，a=10.经检验a=10不符合题意，所以a=-6或a=2.

解析：作出满足已知条件的可行域，如图1所示.

解法1：若a=0，可知不符合题意；若a＜0，由目标函数z=3x+ay得时截距最小，z取得最大值，故8=3-a，解得a=-5；若a＞0，由目标函数z=3x+ay得过A(2,2)时截距最大，z取得最大值，故8=6+2a，解得a=1.综上所述，a=-5或a=1.

解法2：（端点代入法）把A(2,2)，B(-1,1),C(1,-1)代入目标函数z=3x+ay，可分别求得a=1，a=11，a=-5.经检验a=11不符合题意，所以a=-5或a=1.

评注：对线性约束条件下含参线性目标函数最值问题，用端点代入法求解依然成立，但是在求解的过程中要注意代回检验.

1.3 目标函数为非线性目标函数

1.3.1 目标函数为曲线型

解析：作出满足已知条件的可行域，如图2所示.由目标函数z=x2+y得y=-x2+z，当曲线y=-x2+z与x+y=0相切时，z最小，设切点为D(x0,y0)，则y′|x=x0=-2x0=-1，可求得切点为此时对应的，所以z=x2+y的最小值是

图2

评注：目标函数为曲线型，它的最值一般是在切点取到，而不是在线段端点，不可盲目使用端点代入法.

1.3.2 目标函数为距离型

解析：作出满足已知条件的可行域，如图3所示.

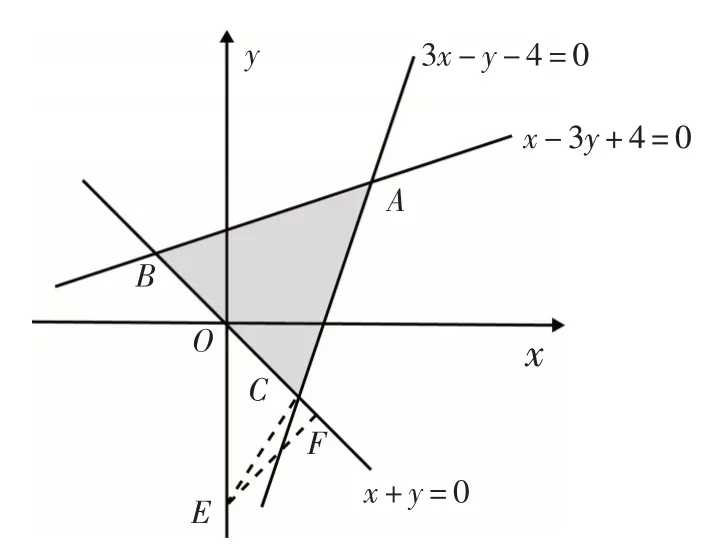
图3

目标函数x2+(y+3)2表示可行域内部的点M(x,y)到点E(0,-3)的距离，作EF⊥BC于点F，则不在可行域内，结合图形可得

评注：对于两点距离型的目标函数，解题时要注意它的最小距离不一定是定点到一条边界线的距离.

1.3.3 目标函数为斜率型

评注：对于斜率型目标函数的取值范围，可以将目标函数对应的直线绕定点旋转，得到斜率的取值范围.

2 改变约束条件

2.1 可行域为曲线型

解析：作出满足已知条件的可行域，如图4所示.由目标函数z=3x+2y得，结合图形可知：当直线相切时，z最大.设切点D(x0,y0)，则得切点为，对应的.所以z=3x+2y的最大值是

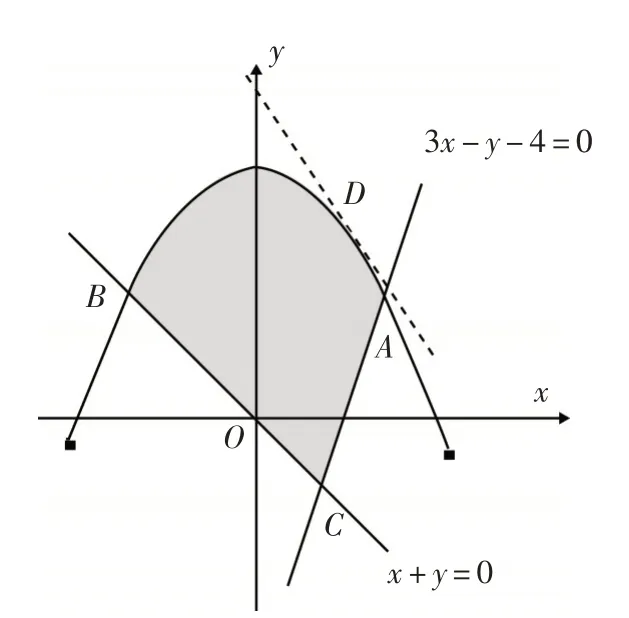
图4

评注：本题中目标函数z=3x+2y的最大值是在切点D处取得，而不是在端点A，B，C处取得.当可行域边界有曲线时，要注意目标函数的最值能否在切点取得.

2.2 约束条件含有参数

解析：作出满足已知条件的可行域，如图5所示.直线ax-3y+4=0过定点斜率目标函数z=3x+2y的最大值是7，则3x+2y=7必过可行域内的点，求出直线3x+2y=7与3x-y-4=0的交点则直线ax-3y+4=0过，代入求得

评注：对于约束条件含有参数的线性目标函数的最值问题，利用逆向思维求解比较简便.

3 线性规划与其它知识交汇

3.1 线性规划与恒成立交汇问题

解析：作出满足已知条件的可行域，如图3所示.可求得A(2,2)，B(-1,1)，C(1,-1)，把A,B,C代入不等式-5≤ax+2y≤8得值范围是[-3,2].

评注：对于线性约束条件下线性目标函数的最值问题，用端点代入法求解较简捷.

3.2 线性规划与不等式交汇问题

评注：本题主要考查了线性规划和基本不等式的有关知识，考查了数形结合思想、推理论证能力和运算求解能力.

图6

综上所述，在高中数学解题教学中实施变式教学，一方面在变中突出不变的解题方法，讲一题、通一类、会一片，能有效促进学生对数学技能的掌握，从而提升学生分析问题、解决问题的数学思维能力；另一方面多角度层层递进的变式问题，符合学生的认知规律，能有效深化学生对数学知识的理解，从而提升学生分析问题、解决问题的数学思维能力.因此，在高中数学解题教学中，实施变式教学能有效提升学生的数学思维能力.