以学生为中心设计解题教学

江苏省奔牛高级中学 蒋 亦 万姝玮 213134

20世纪的学习理论在皮亚杰认知理论的影响下，逐步从以教师为主的“传统范式”转向以学生为主的“学习范式”.新的学习理论强调，知识不是通过教师传授得到的，而是学习者通过意义建构的方式得到的.学生不是被动接受者和被灌输的对象，而是信息加工的主体、是意义的主动建构者.美国教育家布鲁姆认为“以学生为中心”的学习范式，有利于激发学生的创新精神、培养学生的核心素养和关键能力.

新一轮课程改革的核心理念是教育要“以人为本”.落实到教学上就是要以学生为中心，这需要教师在备课时从学生思维出发，针对学生的不同特点，把学生的思维发展与教学内容融合起来；需要教师对教学内容进行有效设计和有机整合.下面以一道含参恒成立压轴题为例，介绍一节以学生为中心的教学设计.

1 第一次教学经历

师：本题难点——参数多，哪个参数最容易处理？

生：x0.只要使得的最大值f(2)=ln2-2a满足条件即可.

师 板 书：-2a+ln2+ln(a+1)＞m(a2-1)-(a+1)+2ln2对任意a∈(1,2)恒成立.即m(a2-1)-ln(a+1)+a+ln2-1＜0对任意a∈(1,2)恒成立.

从大家解答来看，大部分同学选择了分离参数的方法，因为a2-1＞0，所以对任意a∈(1,2)恒成立.

然后就是空白，不会了！那么，如果走分参的路子，下面怎么处理呢？

问题：洛必达法则是高数内容，中学数学课本没有这个结论，因此解答题不能用.也就是说，分离参数的方法不适用本题.恒成立问题常常还用什么方法解决呢？构造新函数，最基本的构造方法“移项”.即m(a2-1)-ln(a+1)+a+ln2-1＜0对 任 意a∈(1,2)恒成立.记g(a)=ma2+a-ln(a+1)-m+ln2-1,a∈(1,2).则g(1)=0,即g(a)＜g(1).

图1

（3）当m≥0时，g′(a)＞0，所以，g(a)在(1,2)单调递增.所以g(a)＞g(1)=0.

2 第二次教学经历

展示学生1分离参数的解答（同上）思考：恒成立问题常常还用什么方法解决呢？

生众：通过“移项”构造新函数.

m(a2-1)-ln(a+1)+a+ln2-1＜0对 任意a∈(1,2)恒成立.记g(a)=ma2+a-ln(a+1)-m+ln2-1,a∈(1,2).则g(1)=0,即g(a)＜g(1).

师：请同学们思考下面怎么办？（5分钟）

生2：（1）当m≥0时，g′(a)＞0，所以g(a)在(1,2)单调递增.所以g(a)＞g(1)=0.（2）当m＜0时，g′(a)=0得，(2ma+2m+1)＜0，所以g(a)在a∈(1,2)单调递减，所以g(a)＜g(1).即g(a)＜0，符合题意.若，g(a)在单调递增.g(a)＞g(1)=0.综上

师：你怎么想到的？

图2

师点评：用导数列表求最值的方法，第1步求导函数的零点；第2步若零点不存在，则原函数单调（用单调性求最值）；若零点存在，则列表求最值.这位同学“用导数列表求最值”解决含参函数最值问题，比老师的“特值法”找分点更容易理解，也深化了我们对课本“用导数列表求最值”的理解.

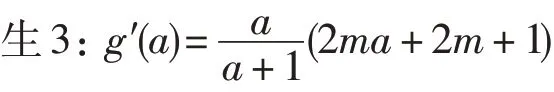
（1）当2ma+2m+1≤0对任意a∈(1,2)恒成立,即所以g(a)在a∈(1,2)单调递减，所以g(a)＜g(1).即g(a)＜0.符合题意.

（3）当m≥0时，g′(a)＞0，所以，g(a)在(1,2)单调递增.所以g(a)＞g(1)=0.综上，

师：你怎么想到的？

生2：根 据g(a)＜g(1)=0,a∈(1,2)猜 想g(a)在a∈(1,2)单调递减,导函数恒负.

师点评：这位同学将考察“导函数的零点”改为讨论“导函数是否恒正或恒负”，第1类当导函数恒正或恒负时，原函数单调；第2类当导函数不恒正或恒负时，有零点存在，则列表求最值.

当导函数零点难求，值域更容易考察时，这位同学处理方法的优越性就显现出来了，让我们对课本“用导数列表求最值”的方法有了更深刻的认识.

师介绍方法3（同上）

点评：老师的“特值法”切入明确分类标准也有优点，比如当导函数的零点和值域都难求时,解题过程可能更简洁.

请同学们小结一下，这类含参恒成立问题的解法有哪些？又是怎么想到的？

相同的教学时间，后者无论是学生参与度，还是课堂容量、教学效果远高于前者.后者的教学过程基于学生能力、以学生为中心，充分调动学生、充分发挥学生能力、贴合学生思维和能力又能培养学生思维与能力的课堂活动，深化对课本知识技能的理解和认识.而前者是基于知识技能的告知、题型解法的灌输.一次次的课堂实践告诉我们，精彩的课堂要让学生自发地成为课堂的主体，鼓励学生观察思考，提问交流，回顾迁移，全方位的围绕学生设计和组织教学活动，从而发展学生思维，深化知识理解，激发学生活力，提高课堂效率.