延伸——在无路可走的时候

安徽省无为第三中学城北校区 朱小扣 238300

数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度及价值观的综合体现，是在数学学习和应用过程中逐步形成和发展的.为此本文将通过阐述延伸思想在解题中的运用，并结合相似、全等等几何知识加以解决难题,揭开部分难题的面纱，让学生在解题中自觉培养和发展数学的核心素养.

例1如图1在△ABC 中，D、E是BC的三等分点，F是AC的中点，且BF与AD,AE分别交于S、T点.求BS:ST:TF的值.

证明：如图2，延长BF至G，使得FG=BF,则四边形ABCG为平行四边形.不妨设BG=20,则BF=10.由△BTE∽△GTA得：

此类问题很多，在高中用向量知识可以解决，但还是构造相似法简单.

例2 如图3，正方形ABCD中，E在AB上，EF//BC交BD，CD于G，F，点M,N分别为DG,EC的中点，若DF=2,BN=13,求证:∠EMC=90°

图1

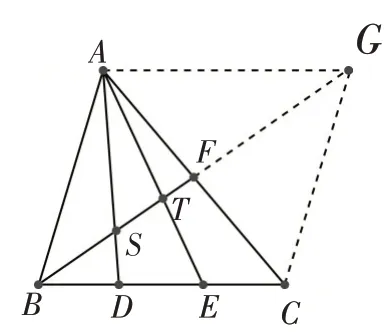
图2

图3

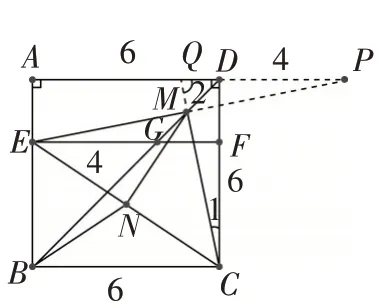
图4

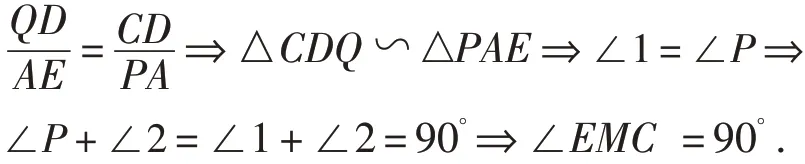
此题表面看很难直接证明∠EMC =90°，无法找到相似与全等的三角形，但延长之后，就很容易找到相似的三角形和问题的解法.

本题的图较“丑”，但延伸后就很美观，很容易的找到解法,很多人会说本题建立坐标系解会简单些，但笔者觉得一方面建立坐标系在解的过程中有时会“超纲”，很多直线的求法用到了点斜式方程，另一方面要想培养自己的“纯”几何能力，还是延伸后证相似较好.

图5

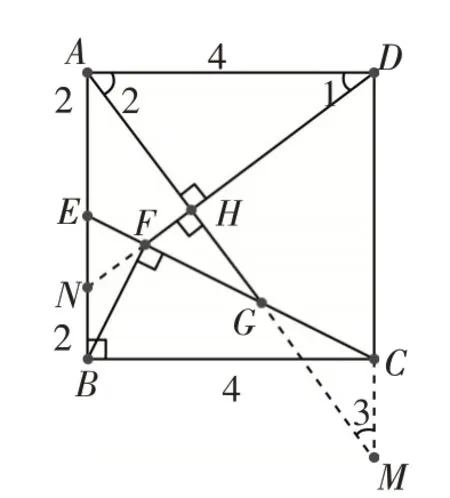
图6

例4如图7在边长为3的正方形ABCD中，E为线段AB延长线上一动点，A关于OE的对称点为点F，过F点作FG⊥CF且FG=CF，连结AG,M为AG的中点.求CM的最小值.

解：如图8延长AO至A′使得OA′=OA，则OA′=OA=OF=OC即A′，A，F，C在圆O上，则圆周角270°=135°,易证△A′FC≌△A′FG(SAS)，于是由 中 位 线 性 质 可 得

图7

图8

本题在解答过程中很多人会找不到方法，像这样延长AO至A′，而后证四点共圆，使问题简单的化归.本文讲的延伸并不是毫无方向的延长，也不是平面上的延伸，而是立体的延伸“登高”，确定出方向再前进！我想这也是培养学生们数学核心素养落地生根的一种好方法，延伸——在无路可走的时候！