一道耐人寻味的期终学业联考题

浙江省绍兴市柯桥区平水镇中学 封 萍 沈岳夫 312050

数学家哈尔莫斯说过“问题是数学的心脏”.对问题进行研究是教师的一项基本功.通过研究，挖掘其隐含的问题的本质，获得丰富的教学资源.这样做，不仅提高教师自身的专业素养，还有利于开阔学生的思路，培养学生的创新能力.本文以2020年1月柯桥区八年级数学期终学业联考试卷中的一道选择题目为例，做一些探索.

1 试题呈现

题目 我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理，如图1所示的矩形由两个这样的图形拼成，若a=3,b=4，则该矩形的面积为（ ）.

图1

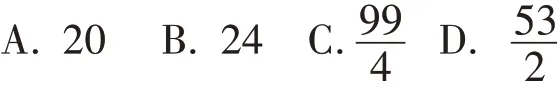
本题源于2018年温州市中考数学试题中的第10题，此题是以数学历史为背景，直角三角形为依托，主要考查了全等三角形、角平分线及勾股定理等知识点，综合性较强.在阅卷后，笔者分析试卷发现此题得分率不高，这引起了我的思考，该题如何解？如何寻找解题的关联点？笔者愿以此文与各位同仁探讨.

图2

2 解法探寻

为方便后面表述，我们先标上相关字母.如图2，根据题意，易得CG=CF=3,AG=AE=4,AC=7,AB-BC=1，CO平分∠ACB，AO平分∠CAB，O为△ABC的内心，设正方形BEOF的边长为x，等等.

思路1 运用勾股定理，借力整体思想

解：根据题意知，在Rt△ABC中，AB2+BC2=AC2，即(3+x)2+(4+x)2=72，整理得x2+7x=12，而矩形ABCD的面积＝(3+x)·(4+x)=x2+7x+12＝24，所以应选B.

评注：此解法先运用勾股定理得方程，再借力整体思想求得答案，这样处理的优点是避免了方程根的求解，繁杂的计算，显得简捷、明了.

思路2运用勾股定理，巧借乘法公式

解：因为AB2+BC2=AC2=72，AB-BC=1，我们若巧用这个乘法公式x2+y2=(x-y)2+2xy的变形，则该矩形的面积=AB·BC=应选B.

评注：在乘法公式学习时，常常会遇到a2+b2=(a-b)2+2ab，a2+b2=(a+b)2-2ab等这些乘法公式的变形.若考生能把平时积累的这些“式”与本题的“形”有机关联起来，那也是一种不错的解题方法.

思路3运用勾股定理，活用AB-BC=1

解：因为AB2+BC2=AC2=72，AB-BC=1，设BC=a，则AB=a+1，所以a2+(a+1)2=72，整理得a2+a=24，而矩形的面积＝a(a+1)＝a2+a＝24，所以应选B.

评注：此解法正是抓住AB-BC=1这个隐含条件，类同思路1而获解.这真是思之愈深，解之愈捷.

思路4抓住三角形内心，巧用面积公式

解：我们都知道有个定理：直角三角形的面积等于内切圆在斜边上的切点分斜边所成的两线段的乘积.即：已知如图3⊙O为Rt△ABC的内切圆，D、E、F分别为AB、AC、BC边上的切点，则S△ABC=AD·BD.如图2，根据题意，因为O为△ABC的内心，G为斜边AC上的切点，显然可巧用这个公式直接秒杀，所以S△ABC=AG·CG=3×4=12，进 而 可知矩形的面积＝2S△ABC=24，故应选B.

图3

评注：此题是借用面积公式直接秒杀.由此可见，考生可以通过自己的自学、吸收、内化，积累这类先进的“武器”，为寻求解决问题的方法贮存能量.

思路5切换视角巧转化，运用同一法求解

解：（视角1：矩形和其内部的图形）由图2易 知4S△AEO+4S△CFO+2SBEOF=S矩形ABCD，即理得x2+7x=12，以下同解法1.

（视角2：△ABC和其内部的图形）由图2知，连结BO，易知S△BCO+S△ABO+S△ACO=S△ABC，整理得x2+7x=12，以下同解法1.

评注：此题的两种解法都是从总量等于分量之和的视角入手，即同一个图形的面积用两种表示法而获解.当然，这需要考生静下心来，认真审题，多方联想，多方检索，做到眼中有“形”，手中有“数”，心中建“模（面积）”，则解法自然来.

思路6重组图形结构，融推理于计算

解：（视角1：将矩形内的图形重拼）根据题意，用分割所得的一个小正方形和两对全等的直角三角形重新构成如图4的图形，显然，所构成的矩形ABCD与原矩形是全等的，显然，而S′=ab=12，所以原矩形的面积S=2S′=24，故应选B.

图4

（视角2：将矩形裁剪旋转重拼）将△ACD绕点C逆时针旋转90°得到如图5，连结AA′，因为AC=7A′作A′H⊥AB于点H，则AH=1，则A′H2==48.5，则原矩形面积=48.5-24.5=24，故应选B.

评注：所谓重组图形结构就是根据图形结构特点，适当对图形进行剪拼（如图4）或重新组合（如图5）来解几何题的一种方法.当然运用此法不仅需要具备解答基本几何图形的基本功，更重要的是还要有识图、分割、拼凑、平移、旋转以及重新组合图形的能力.若一旦掌握，则常常会产生一种“柳暗花明又一村”的解题意境.

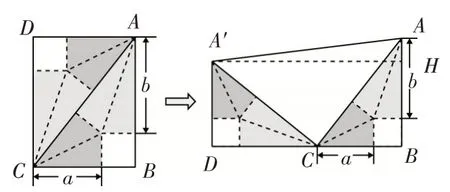
图5

思路7探寻知识关联，创新思维视角

解：用两个原矩形进行重新拼图如图6，则可得到“弦图”，即四边形ACDE与四边形GFBH均为正方形.由图易知AC=7，

图6

评注：此题的解法是将图形补成定理的图形或其他一些基本图形，是一种重要的解题经验，也是添加辅助线的一种重要策略.通过进一步思考，如果从图形的结构出发、联想，则可以将原图补成图6，得到“弦图”（两个正方形有共同的中心），从而获解.由此看出，这种“补形”策略，是通过对题目的深入分析，或联想，或转化，挖掘知识模块内蕴的思想方法，是一种经验的“喷薄”.让人不禁感叹，几何构造之神奇，探索无止境.

通过对这道选择题的研究，笔者得到了一些启发：如何让考生把平时积累的几何模型能在考场中迅速“释放”出来，值得一线教师探究.如文中所举的7种思路9种解法，尽管没有固定的“模式”可以套用，但不是“凭空臆造”，而是如何化“陌生”为“熟悉”的基本图形，并运用基本图形分析法进行解题.由此可见，解题时如果能从多个角度思考、联想问题，将有助于我们巩固知识，掌握方法，以达到摆脱题海，事半功倍之效.因此，作为一线教师在平时的课堂上要把常规的解法教给学生，使学生打好扎实的基础，与此同时，教学中也应该打开思路，多发问，多根据题目问题需要提出合理的目标或适当的变式，使学生在尚未形成固定和完善的思维方式时，充分调动学生的思维积极性和主动性，去思考问题，进而产生不同的想法和解法，从中找到符合自己的认知特点的“自然解法”.