用因式分解处理一类函数零点问题
2020-03-09云南省玉溪第一中学李富春653100
云南省玉溪第一中学 李富春 653100
在导函数中,有一类函数零点(方程实根)问题,直接整体求导、分离参数、分离函数、局部分离函数,计算量都很大,甚至几乎不能求解.若用因式分解,将大大减少计算量,能快速求解,且是通法.下面举例说明.
例1 函数f(x)=(x2-ax)ex-ax+a2(e为自然对数的底数,a∈R,a为常数)有三个不同零点,则a的取值范围是( ).

解析:令f(x)=0,则(x2-ax)ex- ax+a2=(x-a)(xex-a)=0,故f(x)=(x2-ax)ex-ax+a2有三个不同零点⇔x-a=0或xex-a=0共有三个不等根⇔直线y=a与y=x和y=xex的图象共有三个交点.
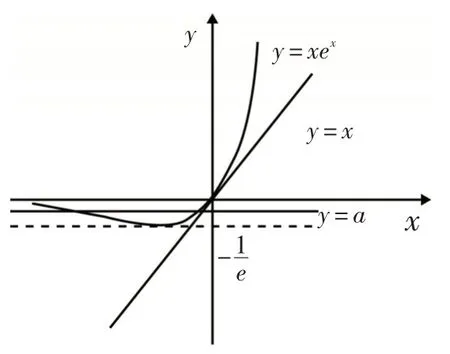
图1
在同一坐标系中,作出y=x与y=xex的图象,由直线y=a与y=x有一个交点,故直线y=a与y=xex有两个交点.
令g(x)=xex,则g′(x)=(x+1)ex,故g(x)在(-∞,-1]递减,在(-1,+∞)递增,且g(x)min=如图1,当时,直线y=a与y=xex有两个交点;当a>0时,直线y=a与y=xex只有一个交点.因此a的取值范围为故选A.
评注:该题是通过因式分解、分离变量,转化为熟悉的基本函数y=a与y=x和y=xex,运用数形结合的数学思想去求解问题,思路朴素、自然.
A.2 B.3 C.4 D.5
解析1:原方程变形为(x2-3)2-2ex-1⋅(x2-3)-3e2x-2=0,分 解 因 式 得(x2-3-3ex-1)(x2-3+ex-1)=0,则有x2-3-3ex-1=0或x2-3+ex-1=0,即x2-3=3ex-1或x2-3=-ex-,则原方程根的个数可转化为函数的图象与直线y=-1和y=3交点的个数.

图2
或x2-3+ex-1=0,即x2-3=3ex-1或x2-3=-ex-1,即原方程根的个数可转化为函数F(x)=x2-3的图象与函数g(x)=3ex-1和函数h(x)=-ex-1的图象交点的个数,在同一平面直角坐标系中画出这三个函数的图象,如图3所示,显然F(x)=x2-3与h(x)=-ex-1的图象有2个交点.
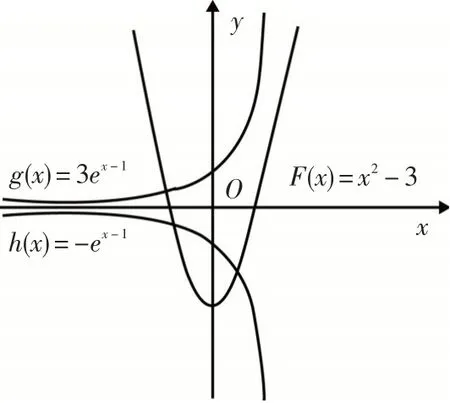
图3
当x≤0时,函数F(x)=x2-3与g(x)=3ex-1的图象有1个交点,当x>0时,令函数,则,当0<x<3时,f′(x)>0,当x>3时,f′(x)<0,所以当x=3时,f(x)取最大值,且最大值为?,即,则即3ex-1>x2-3,即当x>0时,函数g(x)=3ex-1的图象都在函数F(x)=x2-3图象的上方,即函数g(x)=3ex-1的图象与F(x)=x2-3的图象没有交点.所以原方程根的个数为3.选B.
评注:解析1思维导图:将原方程变形分解因式→(x2-3-3ex-1)(x2-3+ex-1)=0→x2-3-3ex-1=0或x2-3+ex-1=0→转化为函数的图象与直线y=-1和y=3交点的个数→研究函数的单调性和极值→画出函数f(x)的大致图象→观察图象确定与直线y=-1和直线y=3交点的个数→原方程根的个数.
解析2思维导图:将原方程变形分解 因 式→(x2-3-3ex-1)(x2-3+ex-1)=0→x2-3=3ex-1或x2-3=-ex-1→转化为函数F(x)=x2-3的图象与函数g(x)=3ex-1和函数h(x)=-ex-1的图象交点的个数→在同一平面直角坐标系中画出三个函数图象→观察函数图象及函数特征确定交点的个数→原方程根的个数.
例3(2013年高考安徽卷理科数学第10题)若函数f(x)=x3+ax2+bx+c有极值点x1,x2,且f(x1)=x1,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数是( )
A.3 B.4 C.5 D.6
解析:把f(x)看成一个未知数,利用求根公式因式分解,由3(f(x))2+2af(x)+b=0,得
于是,关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数⇔关于x的方程f(x)=的不同实根个数⇔常数函数与函数f(x)=x3+ax2+bx+c的图象的不同交点个数.
依题意,得x1,x2是关于x的方程3x2+2ax+b=0的两个不同实根,所以x1,x2=此时函数f(x)=x3+ax2+bx+c的模拟图象如图4.这时常数函数和与函数f(x)=x3+ax2+bx+c的图象的不同交点个数是3⇔关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数是3.当x1>x2时,此 时 函 数f(x)=x3+ax2+bx+c的模拟图象如图5.这时常数函数与函数f(x)=x3+ax2+bx+c的图象的不同交点个数是3⇔关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数是3.

图4

图5
综上,选A.
评注:(1)此题的姊妹题是2013年高考安徽卷文科数学第10题:若函数f(x)=x3+ax2+bx+c有极值点x1,x2,且f(x1)=x1<x2,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数是().
A.3
B.4
C.5
D.6
(2)此类题型的解法,笔者在各种数学资料中见到的与上述解法都不一样,笔者认为上述解法容易被学生接受.
例4(2009年高考福建卷理科数学第10题)函数f(x)=ax2+bx+c(a≠0)的图象关于直线对称.据此可推测,对任意的非零实数a,b,m,n,p,关于x的方程m(f(x))2+nf(x)+p=0的解集不可能是( )
A.{1,2} B.{1,4}
C.{1,2,3,4} D.{1,4,16,64}
解析:把f(x)看成一个未知数,利用求根公式因式分解,由m(f(x))2+nf(x)+p=0,得=0,所以.从而,关于x的方程m(f(x))2+nf(x)+p=0的不同实数根个数⇔关于x的方程f(x)=的不同实数根个数⇔常数函数与函数f(x)=ax2+bx+c的图象的不同交点个数,如图6.

图6
因为函数f(x)=ax2+bx+c(a≠0)的图象关于直线对称,所以一元二次方程ax2+bx+c=0的解关于直线对称.据此可推测,关于x的方程m(f(x))2+nf(x)+p=0的解仅关于一条直线对称,即对称轴有且只有一条.假若方程的解集是{1,4,16,64},则如1与64关于直线对称,4与16关于直线x=10对称,于是选项D不可能是方程的解集,故选D.
评注:若把关于x的方程m(f(x))2+nf(x)+p=0中的f(x)用ax2+bx+c来替换,然后去判断其方程的根的可能情况,这样一来,不仅运算量繁、大,甚至解答不了.解题时,有路可走,走了以后发现不好走,要立即停下来考虑是否继续往下走?
上述题型源于2005年高考上海卷理科数学第16题:设定义域为R的函数f(x)=则关于x的方程(f(x))2+bf(x)+c=0有7个不同实数的充要条件是( )
A.b<0且c>0 B.b>0且c<0
C.b<0且c=0 D.b≥0且c=0
此类题是2005年高考上海卷涌现出的新题型,是当年的难题,时隔15年,回过头去看看,也仍然不简单.笔者查阅了大量的资料,发现给出的解答非常繁琐,十分抽象,学生很难接受.为了能让同学们有点滴启示和收获,下面笔者给让此题的简解通法.

图7
评注(:1)在此题中b2-4c≠0为什么?留给读者考虑(.2)根据此题的题设,可求出关于x的方程(f(x))2+bf(x)+c=0的7个不同的实数解,也可求出这7个不同实数解之和是多少,怎么求?留给读者去思考.
由上述几例的解答,我们可以总结出:已知函数f(x)的解析式,关于x的方程a(f(x))2+bf(x)+c=0(a,b,c∈R,且a≠0)有几个实数根,求实数a,b,c的取值范围或求方程的实根.解决此类问题的简捷通法是,先利用导函数画出或直接画出函数f(x)的模拟或大致图象,然后把f(x)看成一个未知数,利用求根公式因式分解,由a(f(x))2+bf(x)+c=0,得=0,所以,最后把问题转化为函数图象的交点问题,即考虑常数函数和与已知函数f(x)的图象的交点情况.
新课程理念下,注重解题的通性通法,反对过分技巧化的训练.用上述方法解决此类问题,直观、形象、明了、容易理解、便于操作、易被学生掌握,是一种很好的通法.
