复合函数含参问题研究

安徽省宁国中学 陈晓明 242399

近年来，复合函数含参问题时常悄然出现在高考及各级各类模考的舞台．由于复合函数的多样性及含参问题的复杂性，对学生的思维能力、逻辑推理能力、运算能力等要求较高，对学生的数学基础知识掌握是否扎实、数学思想方法是否能灵活运用都是一个考验.学生普遍害怕此类试题，在考场上经常选择放弃.因此，本文通过实例对此类问题进行研究，以求提供解决此类问题的一些策略和方法．

A.1 B.2 C.3 D.4

分析：这里要判断函数零点的个数与实数a的存在性的关系，遇到函数零点的问题我们通常转化为对应方程的根的问题，进一步转化为两个函数图像的交点问题．这里问题的难点在于函数g(x)是一个复合函数，令g(x)=h(f(x))，它的零点的个数即方程h(f(x))=0的异根的个数．令内层函数t=f(x)，则外层函数为y=h(t)，特别应该引起注意的是内层函数t=f(x)的值域是外层函数y=h(t)的定义域．因此解决此类问题通常要分别画出内层函数和外层函数的图像，然后根据两个函数图像、结合函数性质、利用数形结合的思想来进行思考．

解：因为x≥0时，f(x)=4x3-6x2+1，所以f′(x)=12x2-12x=12x(x-1)，故函数在[0,1]上单调递减，在[1,+∞)上单调递增；另外，x＜0时，f(x)=ex∈(0,1)，所以内层函数t=f(x)的最小值为f(1)=4-6+1=-1．其图像如图1所示，函数t=f(x)的最低点为A(1,-1)，函数的值域为[ - 1,+∞)，即外层函数y=h(t)的定义域为[-1,+∞).令y=h(t)=t2-t+a=0，则t2-t=-a，t∈[ - 1,+∞),方程t2-t=-a，t∈[-1,+∞)根的个数即函数y=t2-t，t∈[-1,+∞)与常数函数y=-a图像的交点个数.如图2所示，函数y=t2-t，t∈[-1,+∞)图像最低点为B

图 1

图2

对于命题1：取-a=-1，即a=1，易知函数y=t2-t，t∈[-1,+∞)与y=-1图像无交点，如图3所示，故方程t2-t=-a无解，进一步可知方程无解，即存在实数a使得函数g(x)没有零点，所以命题1成立．

对于命题2：取-a=2，即a=-2，则由方程t2-t=2解得t1=-1,t2=2，如图4所示．当t=-1时，由上述解法可知x=1；当t=2时，由图像可知对应唯一的自变量x0，如图5所示，因此存在实数a使得函数g(x)有2个零点，所以命题2成立．

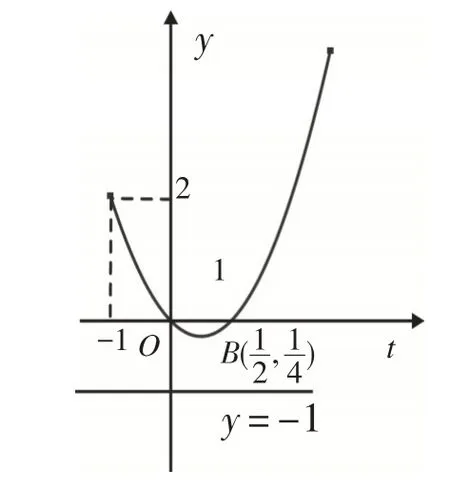
图3

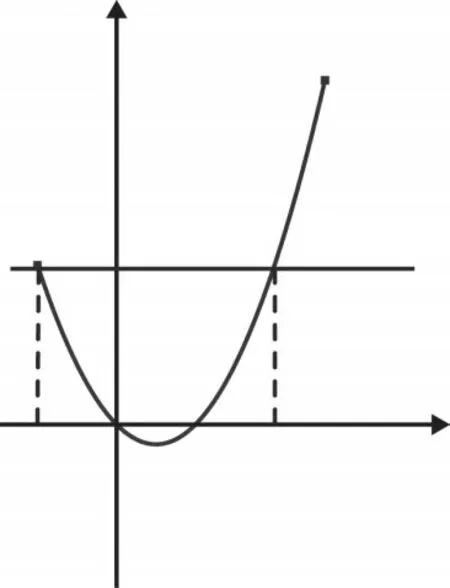
图4

对于命题3：取-a=0，即a=0，则由方程t2-t=0解得t1=0,t2=1，如图2所示．当t=0时，由图1可知对应两个自变量0＜x1＜1,x2＞1；当t=1时，由图1可知对应两个自变量x3=0,x4＞1，因此存在实数a使得函数g(x)有4个零点，所以命题3成立．

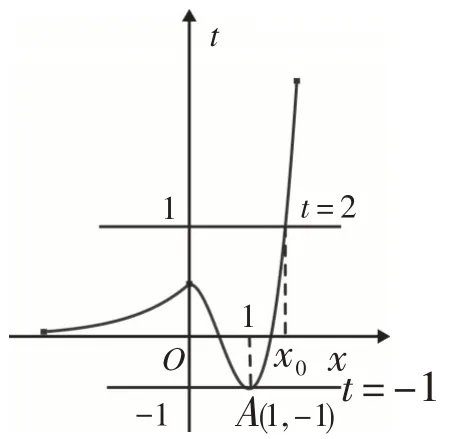
图5

图6

因此，本题正确答案是D．

点评：由上述解法可知，判断复合函数g(x)=h(f(x))零点的存在性，首先要“换元解套”（这里令内层函数t=f(x)，则外层函数为y=h(t)），然后由参数a的值，判断外层函数y=h(t)零点个数及零点的大小（这里通过判断函数y=t2-t，t∈[-1,+∞)与常数函数y=-a图像的交点横坐标来确定），再由该零点的大小（即t的值）及个数通过内层函数t=f(x)的图像来确定复合函数g(x)=h(f(x))的零点的个数.这里渗透了化复杂为简单，化未知为已知，化陌生为熟悉的转化与化归的思想方法，另外还渗透了函数与方程、数形结合、分类讨论等思想方法．

变式 条件不变，问函数g(x)零点的个数可能为哪些值？对应的实数a的范围是什么？

解析：由上述函数图像及解析不难判断有 下 列 结 论：（1），函数g(x)没有零点；（2）当时（此时对应，函数g(x)有3个零点；（3）当时（此时对应t有两个值t1,t2，且，每个t值对应3个零点），函数g(x)有6个零点；（4）当-a=0，即a=0时（见上述解法中对于命题3的分析），函数g(x)有4个零点；（5）当-a∈( 0 ,2)，即a∈( - 2,0)时（此时对应t有两个值t1,t2，且-1＜t1＜0，t2＞1，两个值t1,t2分别对应2，1个零点），函数g(x)有3个零点；（6）当-a=2，即a=-2时（见上述解法中对于命题2的分析），函数g(x)有3个零点；（7）当-a∈( 2 ,+∞)，即a∈( - ∞,-2)时（此时对应唯一的t值，且t＞1，该t值对应1个零点），函数g(x)有1个零点．

A.2 B.3 C.5 D.8

分析：本例中若令g(x)=h(f(x))=f2(x)+af(x)-b2，则它与例1相同的是都是一个二次函数（外层函数y=h(t)）与分段函数（内层函数t=f(x)）的复合函数；不同的是提供条件及求解问题有所不同，当然这里求实数a的最大值可以首先确定实数a的取值范围.由y=h(t)=t2+at-b2＜0可求出t的范围（含参），再由t的范围，结合内层函数t=f(x)的图像和性质，以“不等式恰有1个整数解”为突破口，确定参数b的值，再进一步由t的范围（需对参数a进行分类讨论）确定这1个整数解的值，从而求得自变量x的范围，再得到参数a的具体范围．

解：令t=f(x)，则y=h(t)=t2+at-b2＜0,当b≠0时，因为根的判别式Δ=a2+4b2＞0,所以由韦达定理得对应方程两根之积t1t2=-b2＜0，如图7所示，易知不等式的解集为( t1,t2).显然0∈(t1,t2)，当t=f(x)=0时，由内层函数t=f(x)的图像可知方程有两个整数解0,2，如图8所示，这与“不等式恰有1个整数解”不符，故b=0．

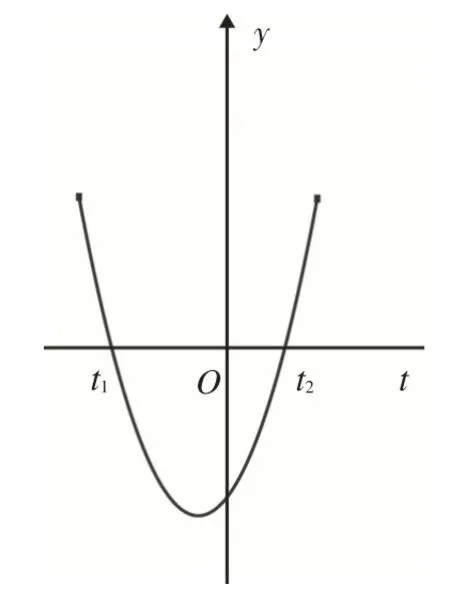
图7

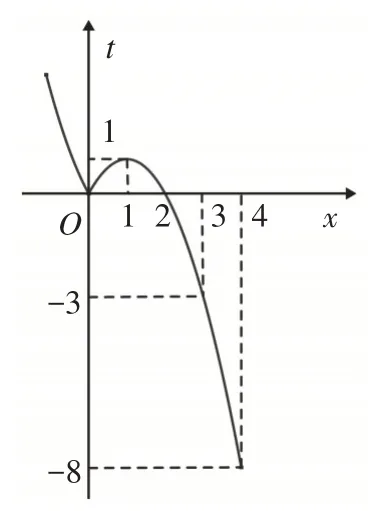
图8

这样不等式可化为y=h(t)=t2+at＜0.（1）当a＜0时，不等式y=h(t)=t2+at＜0解集为(0,-a).①当0＜-a＜1，即-1＜a＜0时，如图9所示，不等式0＜f(x)＜-a解集为(x1,0)⋃( 0 ,x2)⋃(x3,2)，显然其中无整数解，与题意不符，故这种情况不成立；②当-a=1，即a=-1时，不等式0＜f(x)＜1解集为(x1,0)⋃(0,1)⋃(1,2)（其中-1＜x1＜0，因为f( - 1)=3），显然其中也无整数解，与题数与方程、数形结合、分类讨论等思想方法．

变式 条件不变，问函数g(x)零点的个数可能为哪些值？对应的实数a的范围是什么？

解析：由上述函数图像及解析不难判断有 下 列 结 论：（1），函数g(x)没有零点；（2）当时（此时对应，函数g(x)有3个零点；（3）当时（此时对应t有两个值t1,t2，且，每个t值对应3个零点），函数g(x)有6个零点；（4）当-a=0，即a=0时（见上述解法中对于命题3的分析），函数g(x)有4个零点；（5）当-a∈( 0 ,2)，即a∈( - 2,0)时（此时对应t有两个值t1,t2，且-1＜t1＜0，t2＞1，两个值t1,t2分别对应2，1个零点），函数g(x)有3个零点；（6）当-a=2，即a=-2时（见上述解法中对于命题2的分析），函数g(x)有3个零点；（7）当-a∈( 2 ,+∞)，即a∈( - ∞,-2)时（此时对应唯一的t值，且t＞1，该t值对应1个零点），函数g(x)有1个零点．

A.2 B.3 C.5 D.8

分析：本例中若令g(x)=h(f(x))=f2(x)+af(x)-b2，则它与例1相同的是都是一个二次函数（外层函数y=h(t)）与分段函数（内层函数t=f(x)）的复合函数；不同的是提供条件及求解问题有所不同，当然这里求实数a的最大值可以首先确定实数a的取值范围.由y=h(t)=t2+at-b2＜0可求出t的范围（含参），再由t的范围，结合内层函数t=f(x)的图像和性质，以“不等式恰有1个整数解”为突破口，确定参数b的值，再进一步由t的范围（需对参数a进行分类讨论）确定这1个整数解的值，从而求得自变量x的范围，再得到参数a的具体范围．

解：令t=f(x)，则y=h(t)=t2+at-b2＜0,当b≠0时，因为根的判别式Δ=a2+4b2＞0,所以由韦达定理得对应方程两根之积t1t2=-b2＜0，如图7所示，易知不等式的解集为( t1,t2).显然0∈(t1,t2)，当t=f(x)=0时，由内层函数t=f(x)的图像可知方程有两个整数解0,2，如图8所示，这与“不等式恰有1个整数解”不符，故b=0．

图7

图8

这样不等式可化为y=h(t)=t2+at＜0.（1）当a＜0时，不等式y=h(t)=t2+at＜0解集为(0,-a).①当0＜-a＜1，即-1＜a＜0时，如图9所示，不等式0＜f(x)＜-a解集为(x1,0)⋃( 0 ,x2)⋃(x3,2)，显然其中无整数解，与题意不符，故这种情况不成立；②当-a=1，即a=-1时，不等式0＜f(x)＜1解集为(x1,0)⋃(0,1)⋃(1,2)（其中-1＜x1＜0，因为f( - 1)=3），显然其中也无整数解，与题意不符，故这种情况不成立；③当1＜-a≤3，即-3≤a＜-1时，如图10所示，不等式0＜f(x)＜-a解集为(x1,0)⋃(0,2)（其中x1为直线y=-a与函数t=f(x)图像交点横坐标，且-1＜x1＜0，f( - 1)=3），该解集中有唯一整数解1，符合题意，但此时实数a无最大值.④当-a＞3，即a＜-3时，不等式0＜f(x)＜-a解集为(x1,0)⋃(0,2)（其中x1为直线y=-a与函数t=f(x)图像交点横坐标，且x1＜-1，f( - 1)=3），该解集中整数解的个数至少为2个（-1和1），与题意不符，故这种情况不成立．

图9

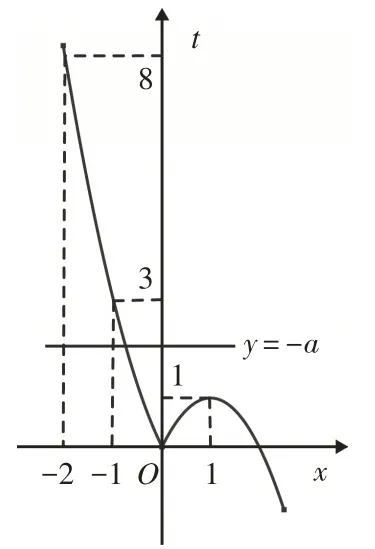
图10

（2）当a=0时，不等式y=h(t)=t2＜0，解集为空集，故这种情况不成立．

（3）当a＞0时，不等式y=h(t)=t2+at＜0解集为( - a,0)，如图9所示，不等式-a＜f(x)＜0解集中“恰有1个整数解”必定为3.因为f(3)=-3，f(4)=-8，所以-8≤-a＜-3，即3＜a≤8，所以实数a的最大值是8．

由（1），（2），（3）知，实数a的最大值是8，故本题正确答案是D.

A.b＜0且c＞0 B.b＞0且c＜0

C.b＜0且c=0 D.b≥0且c=0

解：如图11所示，只要方程f2(x)+bf(x)+c=0中能解出f(x)的两个值，其中一个值等于0（可得c=0）,另一个值大于0（f2(x)+bf(x)=0可 得 f(x)=-b＞0）,故本题正确答案是C．

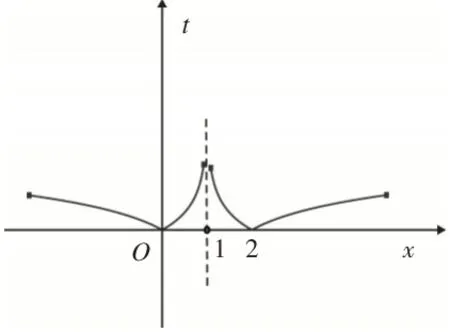
图11

点评：此解法其实使用了换元法的思想，得出方程f2(x)+bf(x)+c=0有7个不同实数解的充要条件是关于t的二次方程t2+bt+c=0有两个不等的实根，其中一根为0（可得c=0），另一根为正数（t2+bt=0，可得b=-t＜0）．这样就自然地将复杂问题化为我们熟悉的简单问题．

规律总结

由上述实例我们不难看出，复合函数含参问题通常与不等式、方程联系在一起，通常其中一个是分段函数，通过提供的条件（如函数零点个数、不等式解集中的特殊解、方程根的个数等），求参数的取值范围（包括最值）．解决这类问题的关键是首先对复合函数g(x)=h(f(x))“换元解套”（这里令内层函数t=f(x)，则外层函数为y=h(t)），然后结合两个函数的图像及性质解决问题．特别引起注意的是内层函数t=f(x)的值域是外层函数y=h(t)的定义域.