一道题，一节课，又不止一节课

孙莉

【摘要】中考复习阶段的备课，重在选题，支持入选例题评讲的理由有很多，比如，贴近某知识点或依据某数学方法或解题策略，或尝试由一道题关联多个知识点、数学思想方法，以达到精选精炼，通过解题发挥例题的价值.

【关键词】解题教学;一课一题;立足题目;探究解法;呈现通法

【基金项目】课题名：南京市教育科学“十三五”规划课题;《“基本图形”在初中几何教学中的渗透策略研究》《波利亚解题思想在初中几何命题教学中的实践与延伸》.

一、案例背景

中考复习阶段的备课，重在选题，支持入选例题评讲的理由有很多，比如，贴近某知识点或依据某数学方法或解题策略，或尝试由一道题关联多个知识点、数学思想方法，以达到精选精炼，通过解题发挥例题的价值.本文将呈现近期笔者在中考二轮复习期间与学生一起探究一道中考题的教学实践与教学思考，与同行们分享.

二、案例呈现

（一）题目

（2017年南京市中考数学第27题）

折纸的思考.

【操作体验】

用一张矩形纸片折等边三角形.

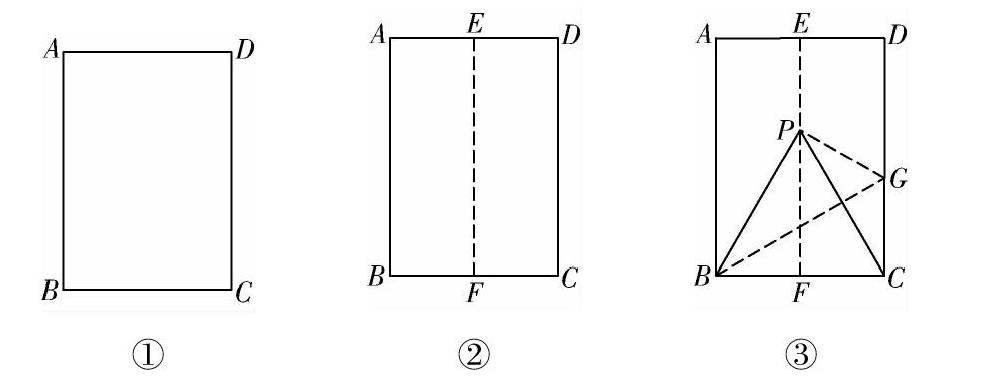
第一步，对折矩形纸片ABCD（AB>BC）（图①），使AB与DC重合，得到折痕EF，把纸片展平（图②）.

第二步，如图③所示，再一次折叠纸片，使点C落在EF上的P处，并使折痕经过点B，得到折痕BG，折出PB，PC，得到△PBC.

①

②

③

（1）说明△PBC是等边三角形.

【数学思考】

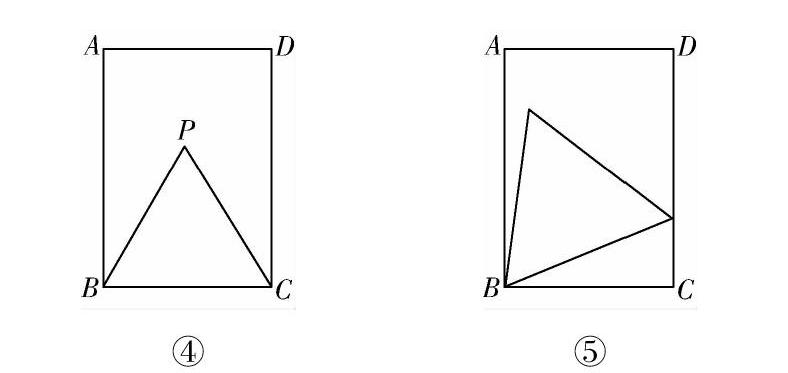
（2）如图④所示，小明画出了图③的矩形ABCD和等边三角形PBC.他发现，在矩形ABCD中把△PBC经过图形变化，可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.

④

⑤

（3）已知矩形一边长为3 cm，另一边长为a（cm）.对每一个确定的a的值，在矩形中都能画出最大的等边三角形.请画出不同情形的示意图，并写出对应的a的取值范围.

【问题解决】

（4）用一张正方形铁片剪一个直角边长分别为4 cm和1 cm的直角三角形铁片，所需正方形铁片的边长的最小值为cm.

（二）“一课一题”的教学记录

教学环节一 围绕等边三角形的热身问题

活动一 展示交流课前作业，学生自评、互评、交流.

课前作业：尝试用不同的方法在A4纸中折出等边三角形.

要求：①虚线画出折痕，实线画出等边三角形;②说明理由.

（课前采图，课上PPT展示）

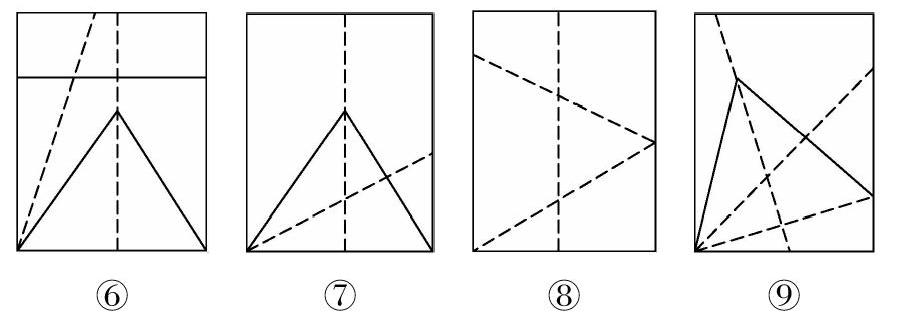
S1-S4的展示如下：

⑥

⑦

⑧

⑨

追问1 如何想到上述折法的？

追问2 解读题目，注意到哪些关键词？如何解读这些关键词？

关键词最近联想

不同方法的多样

A4矩形

折轴对稱：全等，对应边（角）相等;对应点的连线被对称轴垂直平分

等边三角形等边三角形的判定：三边相等的三角形是等边三角形;三角相等的三角形是等边三角形;有一个角是60°的等腰三角形是等边三角形

追问3 哪种折法最便捷？

设计意图：操作体验以体验与发现为载体，重直接经验，更重知识理解.学生通过展示交流在解题教学的意识下将知识结构化，寻找解决问题的通法.虽是折纸也是解题，解题的第一步就是弄清题意，先思再折，先动脑再动手，不同折法的解题切入点不同，但共性是抓住图形的特征以及折叠（轴对称）的性质.折叠性质最易构造的是等腰三角形，再寻找腰底相等比构造角的条件要容易得多.

教学环节二 更大的等边三角形探究

活动二 你能找出更大的等边三角形吗？它们之间有怎样的位置关系呢？

追问1 几何学习中，主要关注图形的哪些方面？

追问2 刚刚折叠产生的图形形状都是等边三角形，它们的大小有什么关系？全等吗？它们的位置又有怎样的关系？

追问3 如何理解“更大”？

追问4 为什么图⑧⑨中的等边三角形比图⑥⑦中的等边三角形更大？

追问5 如何得到“更大”？为什么要旋转？为什么要位似呢？

设计意图：基于活动一以及研究几何图形的基本思路，自然提出活动二.“更大”直观上指面积更大，而对形状相同的等边三角形，进一步要求边长更大.想得到更大的图形一定是要经历位似变换的，而从图④直接放大，显然在矩形中没有足够的放大空间，但只要稍加旋转，问题就迎刃而解了.在寻找“更大”的过程中也会形成一种自觉的反思和心理倾向：有没有“最大”，所以“更大”既是前面活动经验的积累，又是解决后续问题的引申.

如图④所示，小明画出了图③的矩形ABCD和等边三角形PBC.他发现，在矩形ABCD中把△PBC经过图形变换，可以得到图⑤中的更大的等边三角形.请描述图形变换的过程.

追问1 在描述图形变换的过程中，语言叙述如何才能做到完整呢？

追问2 旋转角是任意的吗？

追问3 图④如何得到图⑧呢？

设计意图：追问1是在学生书写的过程中教师介入的，在活动二之后学生已经对为了得到“更大”需要旋转+位似达成了共识，但是有少数学生在书写过程中明显对这两种位似变换的要素有些淡忘导致语言不准确，本质上是由于概念理解不到位.另外，有学生在书写过程中提到“旋转一定的角度”，所以有了追问2，这里旋转的角度是不可以超过30°的，这也是追问3中要提到的“最大”，起初不想给后面“最大”的探究带来干扰，“最大”在活动二中不提及，但基于学情，自然生成了追问3.

教学环节三 最大的等边三角形的探究

活动三 已知矩形一边长为3 cm，另一边长为a cm.对每一个确定的a的值，在矩形中都能画出最大的等边三角形.请画出不同情形的示意图，并写出对应的a的取值范围.

追问1 为什么示意图不止一个？

追问2 为什么要分类讨论？讨论的对象和标准分别是什么？

追问3 约定彩色纸短边是3 cm，根据需要裁出想要的矩形纸片并在其中画出最大的等边三角形.上黑板贴出你所找到的答案，后面展示的学生要求给出的图形与前面的不同.

学生陆续贴出了图⑩到图B13.

⑩

B11

B12

B13

追问4 给出的矩形可以排序吗？

追问5 观察图⑩到图B13，每个矩形中的等边三角形都是最大的吗？例如，图⑩中的等边三角形为什么不是图B14的摆放方式呢？

B14

B15

追问6 还有其他情况吗？图⑩中，随着a的增大，等边三角形会如何变化？

追问7 哪个图中的a比较好求呢？其他图中的a的取值范围又该如何确定呢？

追问8 回看整个寻找“最大”的过程，用到了哪些数学知识、数学思想？

追问9 对上述折纸过程你有什么思考？

追问10 关注了“大小、位置”，“大小”研究完了吗？最大是多大？接下来我们还可以拓展吗？形状可以进一步研究吗？在有限的时间里，你还想研究什么样的问题？你想如何研究？

设计意图：由a的不确定自然联想到要分类讨论，但是这种分类是无序的，在追问1，2中学生自主发现等边三角形的位置摆放随着矩形的长、宽比变化而变化，为了更直观易操作教师介入有了追问3，这在考试过程中也是可行的.追问4可以讓学生更好地用“生长”的眼光看待a，亦为追问6埋下了伏笔.追问5再次点破解决问题的关键是“旋转+位似”，也是“更大”活动中知识的迁移、经验的转化.在追问7中很自然地选择了临界状态并利用三角函数解决了问题.追问8～10是对整个解题的过程的回顾，有知识的、有经验的，更多是题目的生成过程，学生在回答追问10中提出要探究“寻找矩形中的最大等腰三角形、最大菱形、正方形……”等一系列问题，都是源于学生已经通晓几何图形的研究内容“形状、大小、位置”以及找到这类问题解决的通法，即不仅知道了对类似这样的问题该如何思考，更要知道题目的生成过程.

教学环节四 反思拓展

B16

问题解决 用一张正方形铁片剪一个直角边长分别为4 cm和1 cm的直角三角形铁片，所需正方形铁片的边长的最小值为cm.

设计意图：在教学实践中此题作为课后作业.经历了探究矩形中的等边三角形的“有”到“更大”再到“最大”这一过程，学生关注了图形的大小、位置;后续学生们提到寻找最大的菱形、正方形，这是关注了“形状”，这三方面是研究任何一个几何图形应该关注的，这与题目的生成是息息相关的.对外部的四边形从“特殊”的A4纸到“一般”的矩形再到“特殊”的正方形.“特殊”作为解决问题的突破口切入点，以“特殊”为起点进行归纳、概括找到解决一般问题的方法和规律，再反过来指导特殊问题的解决.

三、设计反思

（一）规范推理和书写过程

在平面几何教学中，要关注学生分析问题的思路、推理的严谨性，如在问题1的“说明理由”过程中很多学生书写如下：

由折叠，BF=CF，∠BFP=∠CFP.

又∵∠BFP+∠CFP=180°，

∴2∠BFP=180°，

∴∠BFP=90°，

∴EF垂直平分BC，

∴PB=PC.

又由折叠，BC=BP，

∴△BCP为等边三角形.

却不知由折叠得全等即可得到对应边相等，即如下书写：

由折叠，PB=PC，BC=BP，

∴△BCP为等边三角形.

由此走弯路的现象不难看出学生对折叠的性质还不够明确，所以应当引导学生理解图形变换的性质，重视逻辑推理的过程.此外，还要注重书写格式，发展表述能力，如在问题2中，学生语言表达的不完整还是由于对图形变换的要素不清晰，在几何教学时应注重概念形成的过程并将知识内化、运用，真正做到言之有理、落笔有据.

（二）引导关注解题教学

在A4纸中折出“等边”的方法有很多种，题中是给定明确的折法，要求学生说理即可，笔者不禁思考：如果就给一张A4纸，学生能自行折出等边三角形吗？又有多少种折法呢？哪种折法最便捷呢？这些都该如何思考呢？这就需要教师关注学生分析、解决问题的过程以及方法的优化，在平常教学中坚持“解题教学”，并在该教学活动中，教师给学生要提出一些要求.首先，要求学生学会“咬文嚼字”，学会分析题目中每句话的意思，并且和相关联的知识点建立联想，即由已知想可知，由未知想需知.如在教学环节一当中，对每个关键词的解读，当我们看到“折”，要引导学生想到与轴对称相关的知识点，等等.其次，要学会建立联系，如何将“已知的联想”与“未知的联想”建立联系，一旦发现，问题即可得到解决.最后，回顾反思，看看这道题能不能从“个案”变“类案”，能否举一反三，找到解决问题的通法.

（三）突出与强化分类讨论思想

数学中的分类讨论思想与新课改中提出的培养学生的创新精神与探索精神是一致的，它可以培养学生思维的连贯性和有序性，培养学生完整、细致地分析问题的习惯和探索问题的能力，对养成学生严谨的思维品质有较大的益处，然而在初中数学中分类讨论问题往往是学生不容易掌握好的一类问题，从问题3的课堂实践不难看出，学生由a的不确定知道要分类讨论却不知如何讨论，学生呈现出的构图是碎片式的，以至于对a的取值凭直觉是没有依据的，究其原因，主要是平时的教与学中，对分类讨论的数学思想渗透不够，“要分类吗？为什么？分类的对象是什么？分类的标准是什么？”这是教学中应当培养和渗透的.

（四）深刻品题，关注题目生成

好题是造出来的，也是教出来的，又是学生做出来的.在平常的教与学中，教师和学生往往是一个“打工者”，关注的更多的是解决问题中应用的知识、思想方法，而在本题教学实践过程中，笔者发现学生一直保持着良好的自主探究意识，其原因正是学生明确研究几何图形应关注“形状、大小、位置”这三方面的内容，在折完等边三角形后自然关注它们的“大小、位置”“大小一样吗？有更大的吗？彼此之间又通过怎样的图形变换得到呢？”生成了问题2“更大”之后自然联想到“最大”，在教学过程中也曾经试图在A4纸中连续探究“更大、最大”，再到一般化的矩形，但又有“将学生思维限定”的顾虑，所以把“最大”从特殊的A4纸落到了一般的矩形，生成了问题3.“有了研究‘等边三角形的经验，其他几何图形可以类比吗？”，此时关注“形状”生成了问题4，课堂中学生生成的结果比试题更广泛，因为这节课意在立足题目、探究解法、呈现通法，也是因为这样的一道题，教学过程呈现出来是一节课，又不止一节课，这正是教师所喜闻乐见的.