求解Poisson方程改进的交替方向隐式迭代格式

葛志昊, 刘富豪

(河南大学数学与统计学院，开封 475004)

1 引言

Poisson 方程是一类非常基础且重要的物理方程，在图像修复[1]、计算流体力学[2]、热源识别[3]等领域均有重要应用．因此，构造一种简便而且快速的求解Poisson 方程的算法是很有必要的．交替方向隐式迭代法具有比一般迭代法更高的收敛速度[4,5]，历史上第一个交替方向隐式迭代法是由Peaceman 和Rachford 于1955 年在文献[6]中提出的．1962 年，Varga 将交替方向隐式迭代法用于求解椭圆方程[4]，并将其命名为Peaceman-Rachford iterative method，简称PR 迭代法．该方法广泛应用于各种凸优化问题[7,8]．

经典的交替方向隐式迭代格式[5]在计算大规模问题时，会产生诸多计算上的不便与缺点，如计算程序编写困难、计算耗时较长、计算过程中占用内存过大等．为了克服上述缺点，本文给出了改进的交替方向隐式迭代格式，相比于经典的交替方向隐式迭代格式，改进的交替方向隐式迭代格式通过求解较低维数的矩阵方程，降低了程序实现难度，大大减少了计算量，并进一步证明了改进的交替方向隐式迭代格式与经典的交替方向隐式迭代格式的等价性．因此，改进的交替方向隐式迭代格式更加便于存储，同时克服了经典的交替方向隐式迭代格式在计算上的缺点．

本文其余部分结构如下：在第2 部分的2.1 节，我们介绍经典的交替方向隐式迭代格式；在2.2 节，我们给出改进的交替方向隐式迭代格式；在2.3 节，我们证明经典的交替方向隐式迭代格式和改进的交替方向隐式迭代格式之间的等价性．在第3 部分，我们给出数值算例验证改进的交替方向隐式迭代格式在计算量和程序实现等方面的优势．最后，给出结论总结改进的交替方向隐式迭代格式的优势和不足．

2 改进的交替方向隐式迭代格式

考虑Poisson 方程Dirichlet 边值问题

其中

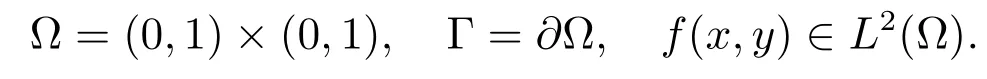
下面，对Ω 进行矩形网格剖分．取定沿x 轴，y 轴的步长h1和h2，作两族与坐标轴平行的直线

两族直线的交点(ih1,jh2)称为网点或节点，记为(xi,yj)．

问题(1)和(2)的五点差分格式为

其中uij表示解函数u(x,y)在节点(xi,yj)处的数值解，fij=f(xi,yj)．

2.1 经典的交替方向隐式迭代格式

首先，我们给出矩阵的自然排列的定义．

定义1给定U =(uij)m×n∈ Rm×n，令

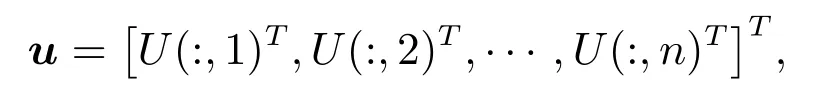
称向量u 为矩阵U 的自然排列，并记作u = {uij}，其中U(:,j)T表示矩阵U 的第j 列的转置．

下面，我们介绍经典的交替方向隐式迭代格式[4,5]：考虑问题(1)和(2)的五点差分格式(3)和(4)，定义矩阵L1和L2分别为

由(5)和(3)，得

于是，经典的交替方向隐式迭代格式(以下简称：经典的迭代格式)为

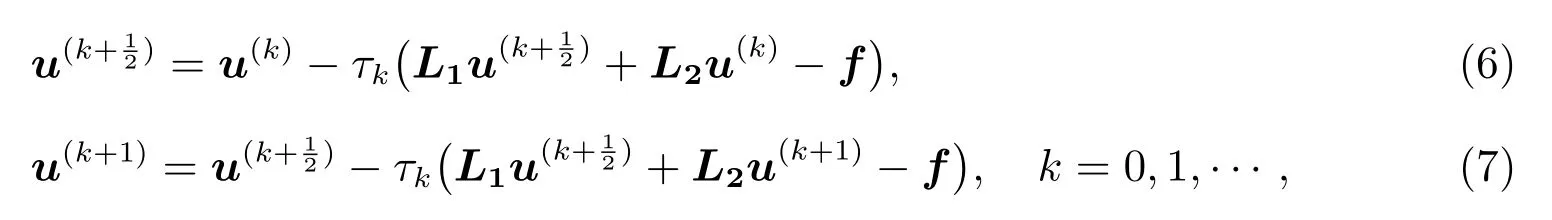
其中τk是迭代参数．按层合并，可得

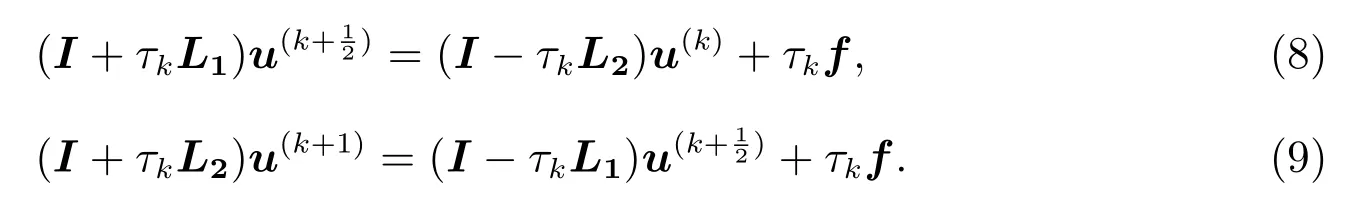
2.2 改进的交替方向隐式迭代格式

接下来，我们给出改进的交替方向隐式迭代格式：考虑问题(1)和(2)的五点差分格式(3)和(4)，定义矩阵分别为

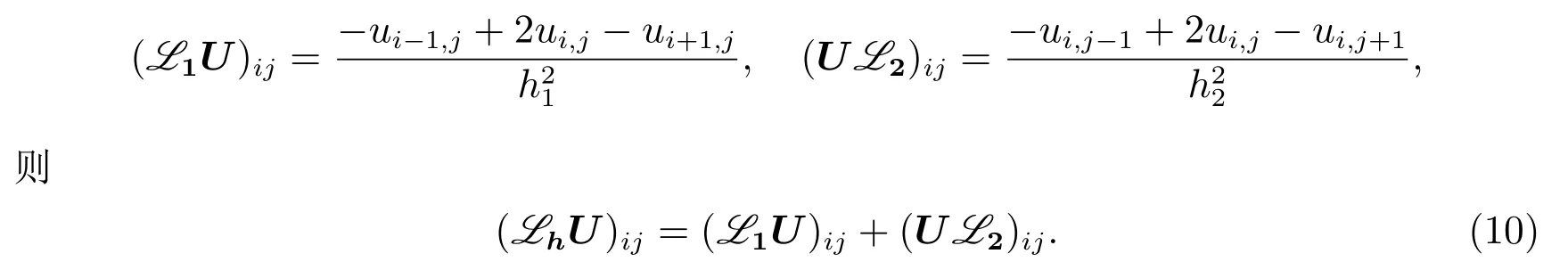
由(10)，可将(3)写成

于是，改进的交替方向隐式迭代格式(以下简称：改进的迭代格式)为

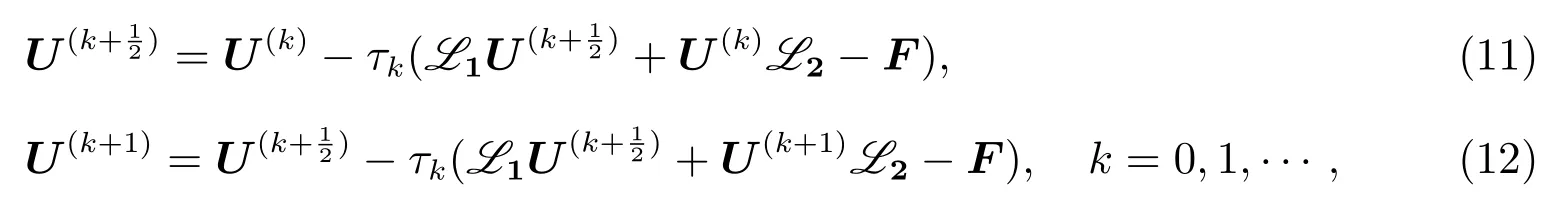
其中τk是迭代参数．按层合并，得

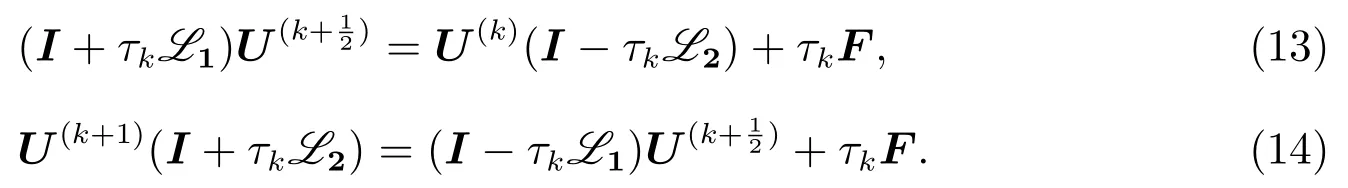
2.3 改进的迭代格式与经典的迭代格式的等价性

定理1改进的迭代格式(13)和(14)与经典的迭代格式(8)和(9)等价．

证明 只需证明(8)与(13)的等价性，可以类似证明(9)与(14)的等价性，这里不再赘述．

考虑内点(xi,yj)处的五点差分格式．在(8)中u 的排列方式为自然排列．因此，点(xi,yj)处的数值解uij对应于向量u 中的第m(j−1)+i 个分量，而对应于矩阵U 第i 行第j 列的元素．

不失一般性，选取(8)中第m(j −1)+i 个方程和(13)第i 行，第j 列的方程．

由 (8)，可知矩阵 I + τkL1的第 m(j − 1)+i 行为

矩阵 I − τkL2的第 m(j − 1)+i 行为

由(15)和(16)，知(8)的第m(j −1)+i 个方程为

同理，可得(13)第i 行，第j 列的方程为

经化简，可以看出(17)与(18)相同．因此，在正则内点处，两种方法建立的方程是等价的．

对于非正则内点处，我们可以在(17)和(18)中取i = 1,m (j = 1,2,··· ,n)和j =1,n (i=1,2,··· ,m)，并将边界条件 u0,j=um+1,j=ui,0=ui,n+1=0 (i=1,2,··· ,m,j =1,2,··· ,n)代入其中得到．于是，两种迭代格式建立的方程是等价的．

2.4 改进的迭代格式的优势

虽然，经典的迭代格式在每一次迭代过程中，只需交替解两个具有三对角系数矩阵的方程(8)和(9)，但L1, L2均为mn×mn 的三对角矩阵，而且L1L2．这不仅会增大问题的计算难度，而且会增加许多计算量．

改进的迭代格式在每次迭代过程中，需要交替求解两个较低维数的具有三对角系数矩阵的矩阵方程(13)和(14)，这等价于求解n 个m×m 和m 个n×n 具有三对角系数矩阵的线性方程组，而且这两个矩阵方程的三对角系数矩阵在U 为方阵的情况下是相等的，区别仅在于：在(13)中，系数矩阵左乘未知矩阵，在(14)中，系数矩阵右乘未知矩阵，相比于经典的交替方向隐式迭代格式，这是比较容易处理的．

为了比较两种迭代格式在实际计算中的不同，现基于Gauss 消去法对求解(8)和(9)与(13)和(14)的过程，进行计算量的预估．若使用追赶法[9]对上面四个方程进行求解，则求解(8)和(9)的算法总计算量为

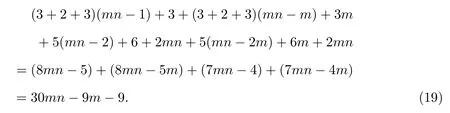
求解(13)和(14)的算法总计算量为

对比(19)和(20)可以发现，在尽可能避开零参与运算的情况下，相比于经典的迭代格式，改进的迭代格式在计算量上减少了很多，表1 和表2 也证实了这一点．事实上，经典的迭代格式在实际计算中，若是尽可能避开零参与运算和存储的情况，则会大大增加程序编写的难度和长度．而改进的迭代格式在这方面，是远远优于经典的迭代格式的．另外，由于改进的迭代格式和经典的迭代格式是等价的，这个结论已在第2.3 节给出证明，所以改进的迭代格式在计算精度方面并没有提升．但改进的迭代格式在数据存储方面，相比于经典的的迭代格式要少得多，而且要比后者方便的多．

3 数值实验

在问题(1)和(2)中，取

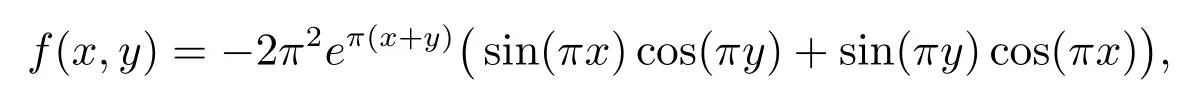
此时，问题(1)和(2)的精确解为

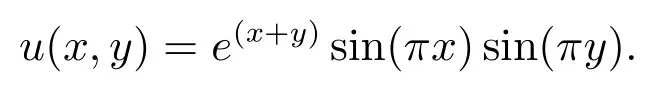
记

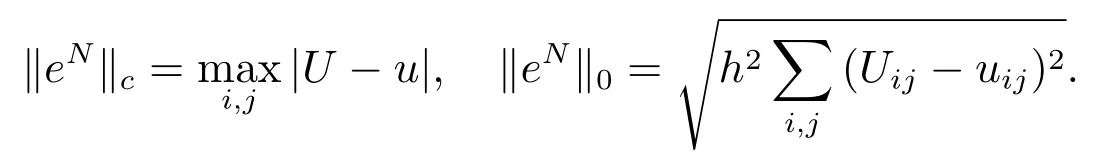
取步长

表1: 经典的迭代格式的误差及运行时间

考虑迭代格式(13)和(14)，取步长

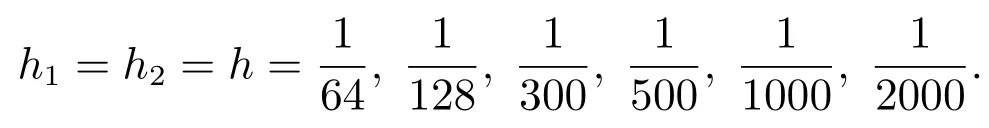
表2: 改进的迭代格式的误差及运行时间

从表1 和表2 可以直观地看出，利用改进的迭代格式的计算误差与利用经典的迭代格式计算误差并没有明显的差异，但在相同的步长下，经典的迭代格式用时远远超过改进的迭代格式，而且两者之间的时间比也随着步长h 的缩小而增大，如：当时，时间比为0.2188/0.1164 ≈ 1.9；当时，时间比为2.1853/0.4411 ≈5.0．对于经典的交替方向隐式迭代格式，当步长时，程序运行时间过长，而改进的迭代格式仍然很好．从图1 和图2 可以看出，步长越小，改进的迭代格式对真解的拟合效果越好．

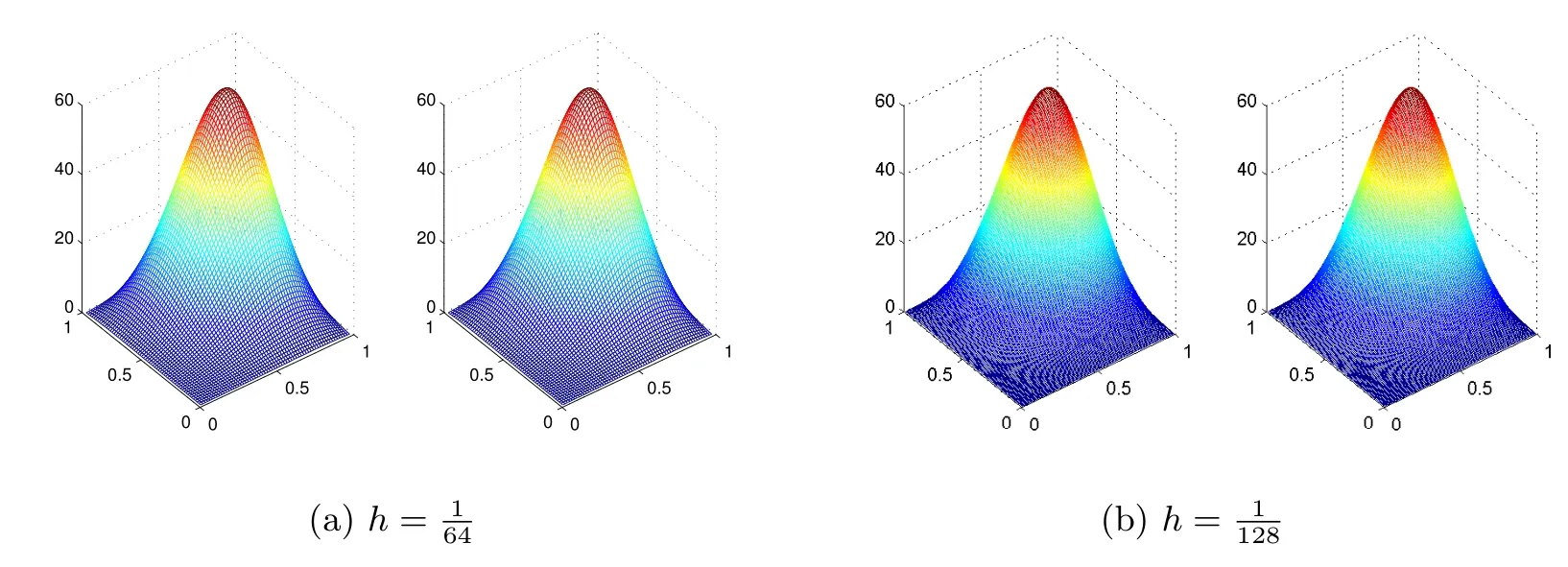
图1: 经典的迭代格式，(a)和(b)中的左图为真解，右图为数值解

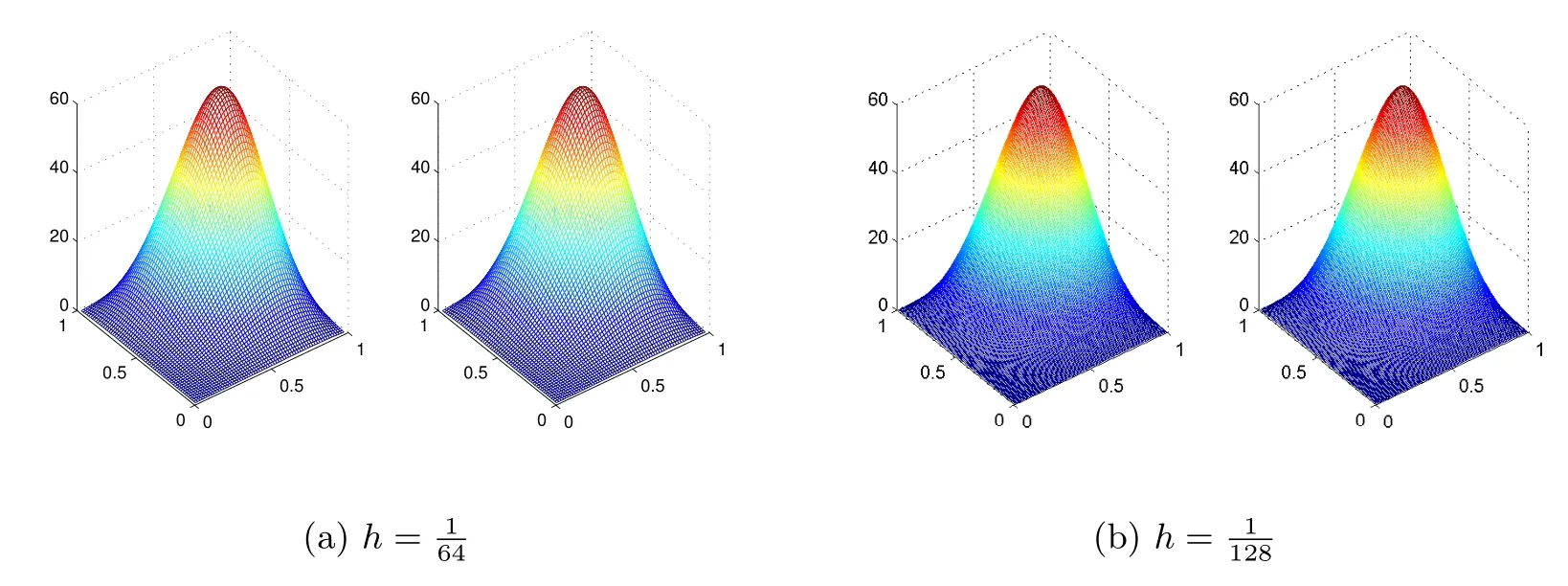
图2: 改进的迭代格式，(a)和(b)中的左图为真解，右图为数值解

由表1 和表2 中的数据可知，两种迭代格式的误差的差值在10−10范围内，并且在以相同的步长和迭代停止条件下，两种迭代格式的迭代步数相等，这说明在不考虑由求解器不同而产生的误差时，每次迭代过程中的有效数据也是等价的，这与定理1 的结论一致．

4 结论

交替方向隐式迭代法是一种具有比一般迭代格式更高的收敛速度的求解Poisson 方程的方法，但经典的交替方向隐式迭代格式在当求解大规模问题时，会产生计算程序编写困难，计算耗时较长，计算过程中占用内存过大等问题．本文给出了改进的交替方向隐式迭代格式(13)和(14)，通过求解较低维数的矩阵方程，降低了程序实现难度，大大减少了计算量．在计算量和程序实现等方面，改进的迭代格式(13)和(14)远远优于经典的迭代格式(8)和(9)．同时，本文证明了两种迭代格式的等价性．因此，改进的迭代格式不仅具有经典的迭代格式在理论分析层面的收敛性，而且在计算上更加简便快速．

然而，与经典的交替方向隐式迭代格式一样，改进的交替方向隐式迭代格式仅适用求解区域为矩形区域或可以转化为矩形求解区域的线性问题和半线性问题．本文以五点差分格式为基础，导出改进的交替方向隐式迭代格式，事实上，仿照文中的过程，可以以九点差分格式导出更高阶的交替方向隐式迭代格式，九点差分格式下的改进的交替方向隐式迭代格式与五点差分格式下的迭代格式在计算过程方面的区别仅在于：五点差分格式得到的迭代格式需要求解两个系数矩阵为三对角矩阵的线性矩阵方程，而九点差分格式下的迭代格式需要求解两个系数矩阵为五对角矩阵的线性矩阵方程，在两个方向取的节点数相同的情况下，同一差分格式对应的矩阵方程系数矩阵是相等的．