广义Tanh函数法中Riccati方程和sine-Gordon方程的新解及其新应用

林府标, 张千宏

(贵州财经大学数统学院，贵阳 550025)

1 引言

1.1 Riccati方程(1)的已知显式解析解

物理或工程等中的数学模型通常可归结为偏微分方程，这些方程的各种性质，如显式解析解等，特别是行波解可以很好的描述各种物理现象，如振动、传播等．但由于非线性偏微分方程的复杂性和多样性，至今仍有大量的重要方程无法求出显式解析解，即使已经求出显式解析解，也各有各的技巧和方法，至今仍没有一般统一的解析求解方法．

直接构造非线性偏微分方程解析解最有效的方法之一为Tanh 函数法[1–3]，其算法的基本原理基于绝大部分有物理意义的非线性偏微分方程的行波解都可以表示成Tanh 函数的多项式，而广义的Tanh 函数法[1–3]核心思想是充分利用带有一个参数b 的Riccati 方程

进行反复计算，将含φ 的所有导数项转化成关于φ 的代数多项式，因此非线性偏微分方程的精确求解问题就可以转化成代数多项式方程根的探讨问题，从理论上说，求解一个非线性代数方程或方程组总比求解一个非线性偏微分方程相对容易．另外，利用Riccati 方程(1)的一个好处是参数b 的符号可以判断所得行波解的数量和形状．

众所周知Riccati 方程(1)具有三角函数和有理函数类型的显式解析解[3]．事实上用Matlab 易验证Riccati 方程(1)更具有表1 中的三角函数和有理函数类型的一般解．

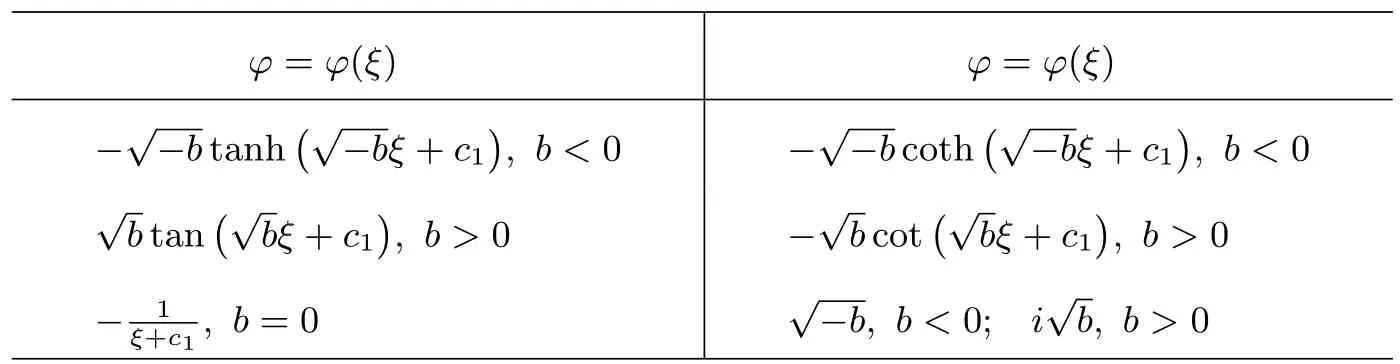
表1: 带参数b 的Riccati 方程(1)的解，其中c1 ∈R, i2 =−1

另外，文献[4]给出了Riccati 方程(1)的十二种类型的显式精确解，为了方便研究和应用，将其结果列于表2．

表2: 带参数b 的Riccati 方程(1)的解，其中ε=±1, i2 =−1

1.2 Riccati方程(1)的新显式解析解

为了利用广义Tanh 函数法结合Matlab 符号运算和吴消元法构造非线性偏微分方程多种形式的新行波解，在文献[4]的工作基础上运用试探函数法结合Matlab 计算找到了Riccati 方程(1)的八种类型的新显式解析解，其结果列于表3．

表3: 带参数b 的Riccati 方程(1)的新解，其中ε=±1,a1,a2 ∈R

2 Tanh函数法结合Riccati方程的新解求sine-Gordon方程的新行波解

sine-Gordon 方程[5]

不仅具有丰富的物理与几何背景以及悠久的历史，而且具有许多有趣的现象，因而成为无穷维动力系统中的一个重要的模型．sine-Gordon 方程(2)最早是从一类实际问题归结为Gauss 曲率K = −1 的曲面几何研究中得到的[5]，可用于描述Josephson 传输线中的磁通量子[6]、共振介质中的超短脉冲传播[7]等．后来发现它在非线性光学、生物物理、离子物理、非线性晶格和超导物理的Josephson 结构等物理领域也有着广泛的应用[5,8–12]．由于经典sine-Gordon 方程(2)与流体中的浅水波方程有相似的波动性质，所以也称为非线性波动方程．

目前为构造sine-Gordon 方程的精确解已发展了许多解析求解的方法[5,8–11,13,14]．齐次平衡法也称拟解法，也是构造非线性偏微分方程行波解的一种有效方法[3,15–17]．为了探求sine-Gordon 方程的行波解，作变换

把(3)代入(2)得约化二阶非线性常微分方程为

注意到(3)，进一步假设约化方程(4)的解的表达式为

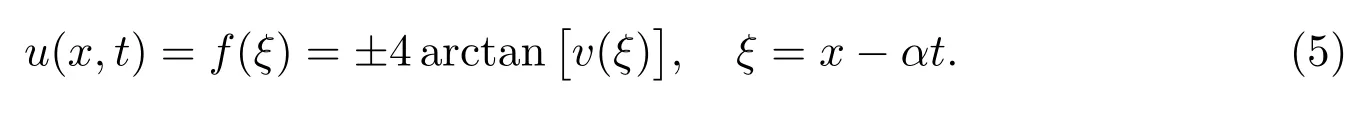
从而通过计算得

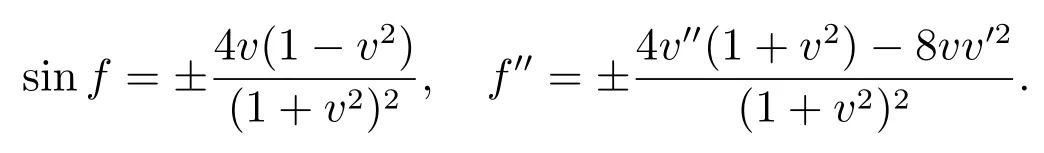
因此，约化方程(4)转化成

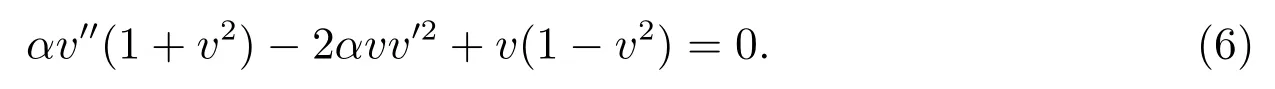
根据Tanh 函数法[1–3]的关键思想，v′′与v3需平衡，于是可假设方程(6)的解的表达式为

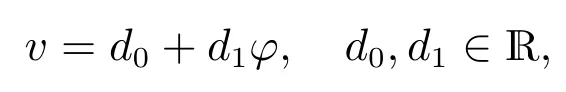
其中φ 满足Riccati 方程(1)，并且将其代入(6)得关于φ 的多项式函数方程，令φj(j =0,1,2,3,4)的系数为零得关于d0,d1,b 的非线性代数方程组

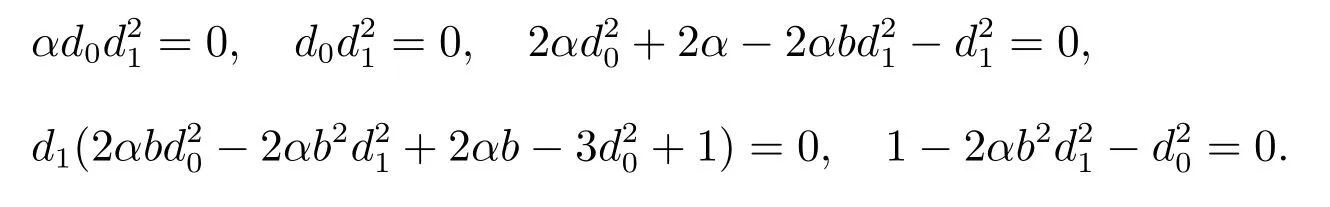
利用计算机代数中的吴消元法[18]，结合Matlab 编程计算解得

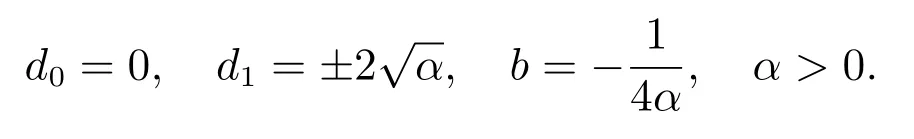
注意到b < 0，应用表1 至表3 中Riccati 方程(1)的相应解且取得到方程(6)的许多解，其结果列于表4．因此，sine-Gordon 方程(2)的行波解或函数(5)的具体解析表达式为

其中 vj(j =1,2,··· ,12)，见表4．

表4: 方程(6)的解，其中b=−, α >0, ε = ±1, c1,a1,a2 ∈ R

表4: 方程(6)的解，其中b=−, α >0, ε = ±1, c1,a1,a2 ∈ R

v1 =−tanh(√−bξ+c1)v7 = 5−4 cosh(2√−bξ)3+4 sinh(2√−bξ)v2 =−coth(√−bξ+c1)v8 = −2√√tanh(2 ξ)+coth(−b −b v3 = −[tanh(2√2 ξ)−bξ)+iεsech(2√−bξ)]v9 = a1−e2√−bξ a1+e2√−bξ v4 = −[coth(2√ √−bξ)+ εcsch(2√−bξ)]v10 =a21+a22−a1 cosh(2√a1 sinh(2√ −bξ)−bξ)+εa2 v5 =−1α−bξ)−1 v6 = 2√2 ξ)+coth(√−b[tanh(√2 ξ)]v11 = tanh(√−b √ −bξ)+2a1b√2 a1−b tanh(√α[b−√−b tanh(√v12 = −(a1 sinh(2√−bξ)]−b tanh(√1+√a22−a21)−bξ)+ε√−bξ)a1 cosh(2√−bξ)+a2

另外，运用试探函数法结合Matlab 编程计算发现约化方程(6)有指数函数类型的解因此得sine-Gordon 方程(2)的解或(5)的解析表达式为

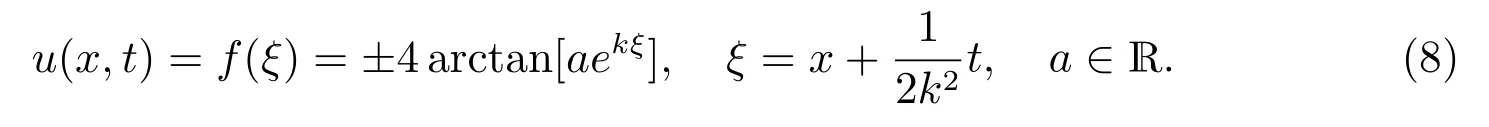
下面对约化方程(4)做一些简化和变换，令变换f = 2ω，这里f 是方程(4)的解，则约化方程(4)重新改写成

在方程(9)两边同时乘以ω′，得

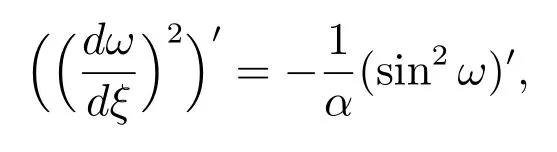
然后积分一次可得

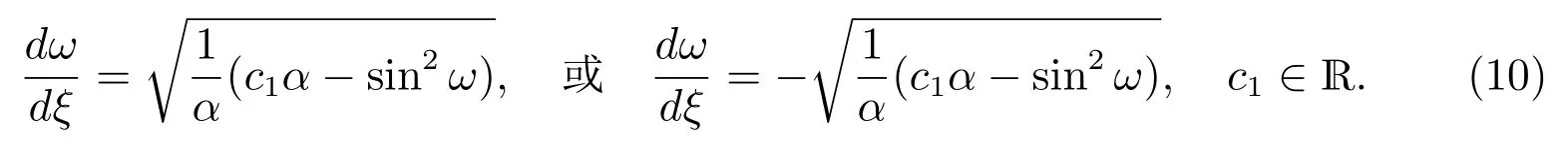
作为变换(10)的特殊情况，令α=−1, c1=0，且在方程(10)中取正号可得

利用分离变量法得方程(11)的一般解和相关恒等式为

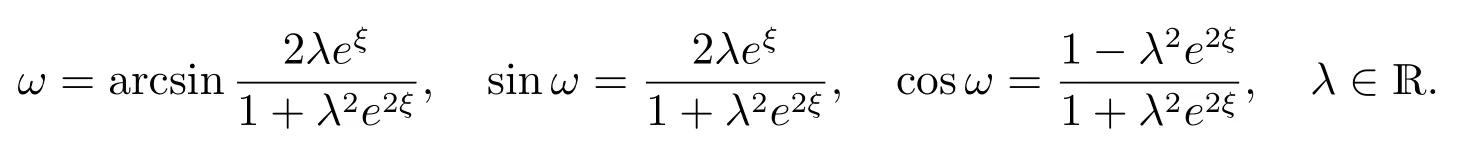
特别地，取λ=1，有

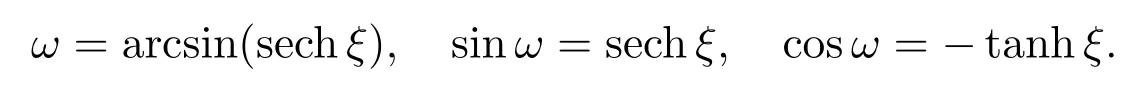
类似地，取α=1, c1=1，且在方程(10)中取正号得

类似前一种情况运用分离变量法可得方程(12)的通解和相应恒等式为

特别地，取λ=1，得到

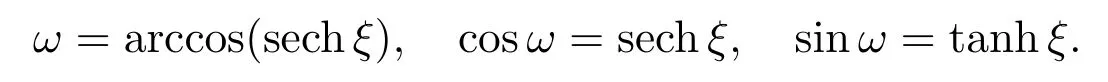
所以，注意到(3)和变换f =2ω，得方程(2)的相应行波解为

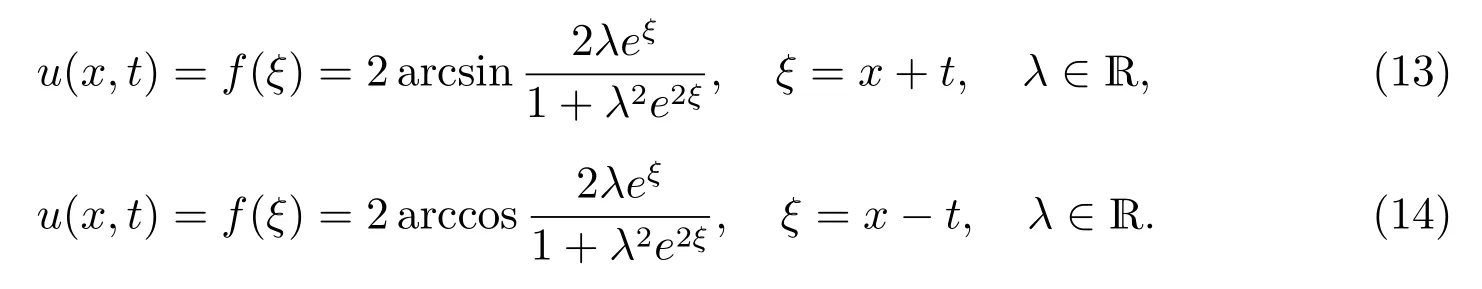
注意到在表3 中带参数b 的Riccati 方程(1)的新解在文献[4]中没有给出，sine-Gordon 方程(2)的显式行波解(7),(8),(13)和(14)在文献[3,5–11,13,14]中也没有给出．sine-Gordon 方程(2)的行波解(14)的空间图像，见图1(a)所示，而该行波解的u 在ξ−u 平面上的平面图像，见图1(b)所示，这里参数λ=1．

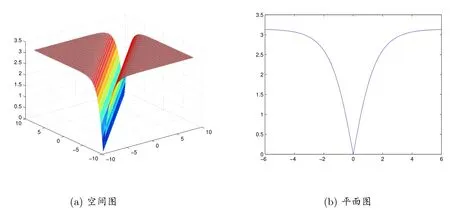
图1: sine-Gordon 方程(2)的行波解(14)，参数λ=1

变换(10),(11)和(12)分别是约化方程(4)的简化变换形式，而约化方程(4)相应这些变换的显式解析解分别为(7),(8),(13)和(14)．作为一种应用，它们可以用于求解非线性偏微分方程

假设方程(15)的行波解的表现形式可以写成

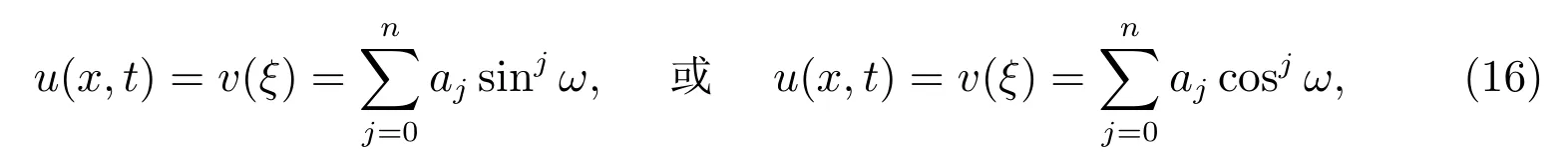
这里ξ =x−αt, aj,α ∈ R(j =0,1,··· ,n)，而ω 满足变换方程(10)或(11)或(12)，n 为一正整数，可以通过平衡方程(15)的非线性项和最高阶导数项得到，而α, a0,a1,··· ,an为待定实参数．将(16)代入(15)并令sinjω, sinjω coskω 或cosjω (j,k = 0,1,···)的系数为零可以得到关于α, a0,a1,··· ,an的代数多项式方程组，利用吴消元法[18]结合Matlab 编程计算，由此可解得待定实参数α, a0,a1,··· ,an．

虽然正余弦函数法或三角函数法[19,20]与Tanh 函数法[3]的关键思想基本类似，但对探求一些非线性偏微分方程的精确解，广义的正余弦函数法或三角函数法(16)往往比Tanh 函数法更简洁，下面通过探讨KdV 方程(17)的新行波解来具体体现．

3 正余弦函数法结合sine-Gordon方程的新解求KdV方程的新行波解

众所周知，KdV 方程

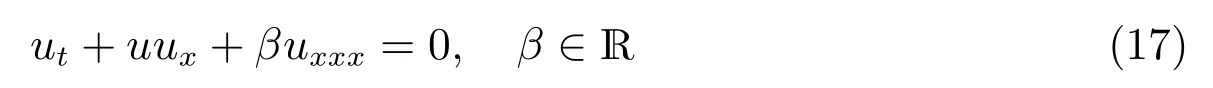
是非线性数学物理中的一个基本流体模型方程，主要用于描述湍流和不稳定现象，它是1895 年荷兰数学家Korteweg 和de Vries 研究浅水波运动时提出的一个数学模型，其详细推导过程可查询相关文献[21]．如今不断发现，相当广泛的一类描述弱非线性作用下的波动方程，在长波近似和小的且为有限的振幅假定下，都可归结为KdV 方程(17)，如冷等离子体的磁流体波的运动，非谐振晶格的振动，等离子体的离子声波，在液、气两种混合态的压力波的运动，在一个管底下部的流体的运动，在低温下非线性晶格的声子波包的热激发，在弹性杠中的纵向色散波的传播等．

随着KdV 方程(17)在流体力学、等离子体物理、气体动力学等领域的重要应用，也是物理学家和数学家感兴趣的方程之一[22]．KdV 方程(17)的行波解的探讨在研究非线性物理现象中起着重要的作用，新的精确行波解可以帮助人们发现新的现象，寻找更多新的显式解析解一直是非线性科学研究的主要内容之一．到目前为止，仅发现了KdV 方程(17)一种形式的孤子解．近年来，发展了许多行之有效的构造KdV 方程(17)精确解的方法，如齐次平衡法[23,24]，双曲函数展开法以及广义的Tanh 方法[3,25]，直接解法[26]等．

假设 u=v(ξ), ξ =x+ct, c ∈ R 是 KdV 方程 (17)的行波解，于是 KdV 方程 (17)约化为常微分方程 cv′+vv′+ βv′′′= 0，两边关于变量 ξ 同时积分一次，并令积分常数为零，可得

注意到变换方程(10)和正余弦函数法(16)的求解思想，v2和v′′需平衡，从而方程(18)的解的表达式可假设为

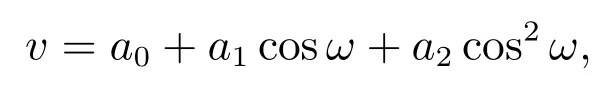
其中aj(j =0,1,2)为待定实参数，而ω 满足变换方程(10)．因此，由计算可知

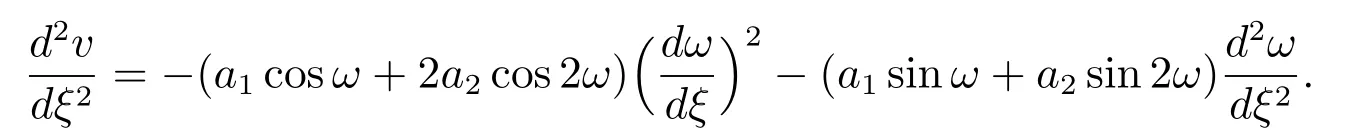
把上式和(9)以及(10)代入(18)，利用Matlab 计算整理得关于cos ω 的三角函数方程

令cosjω(j =0,1,2,3,4)的系数为零，得关于a0,a1, a2和c 的非线性代数方程组

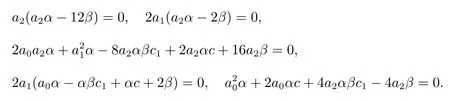
利用吴消元法[18]结合Matlab 计算解得a1=0,和

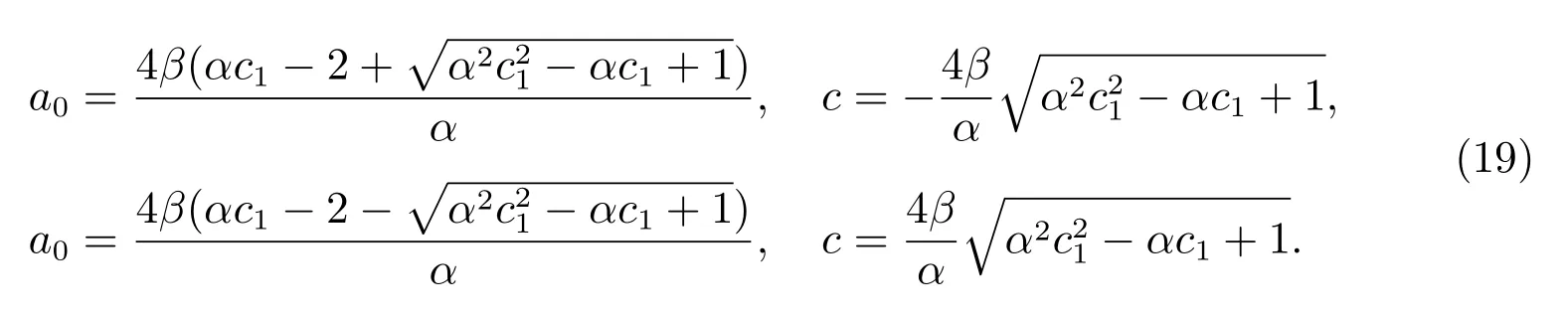
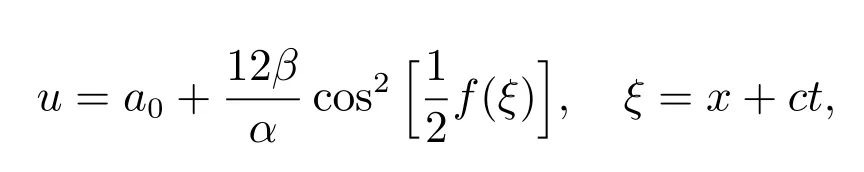
其中a0和c 见(19)．特别地，利用方程(4)的解(13),(14)和(8)得到KdV 方程(17)的行波解的具体显式表达式为

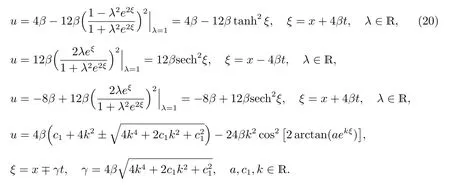
注意到约化方程(4)有许多种类型的解(7)，因此，类似地利用(7)可求得KdV 方程(17)的多种形式的新行波解．在文献[3,22,26]中没有给出上述KdV 方程(17)的显式行波解．在KdV 方程(17)中选取色散系数β = 1，其行波解(20)的空间图像，如图2(a)所示，而u 在ξ −u 平面上的平面图，如图2(b)所示．

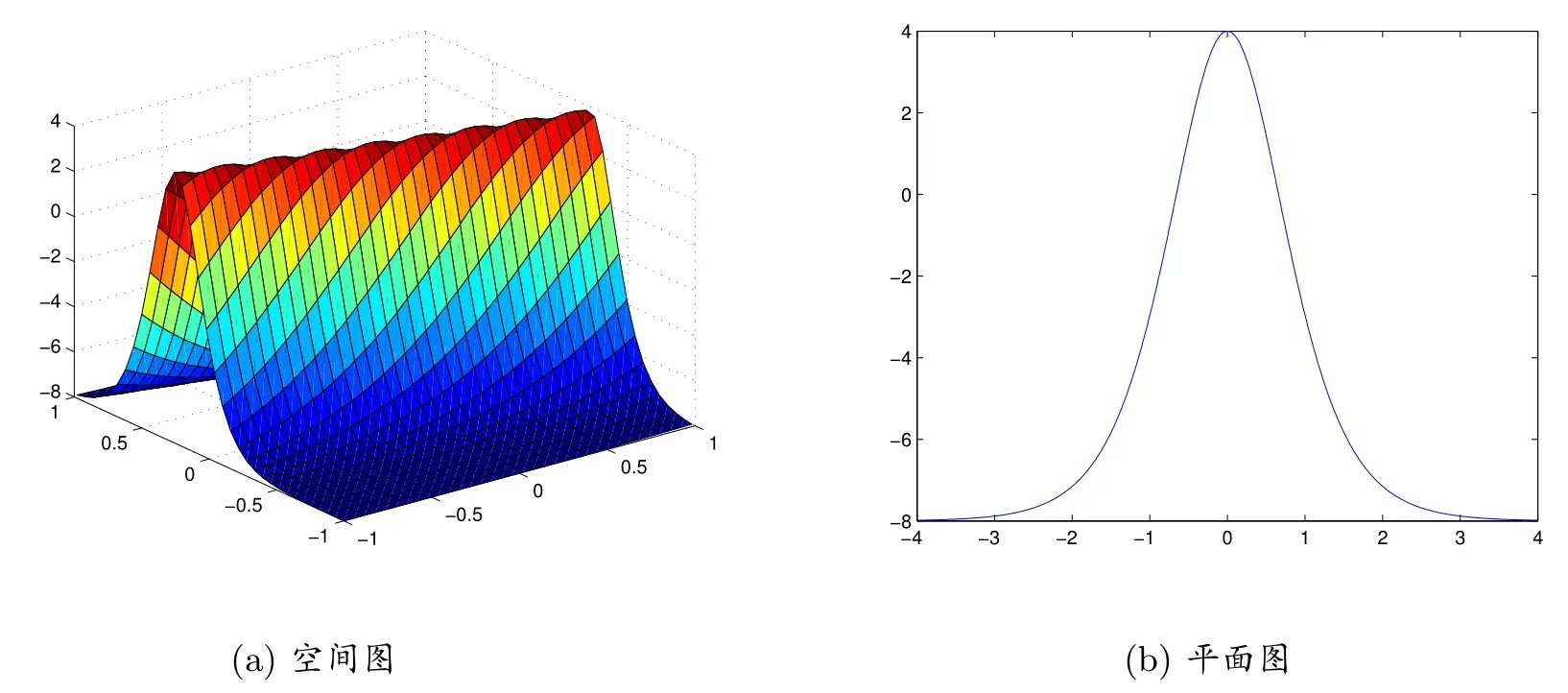
图2: KdV 方程(17)的行波解(20)，色散系数β =1

4 结论与探讨

本文首先利用表3 中Riccati 方程的八类新解析解结合广义Tanh 函数法给出了一维sine-Gordon 方程的许多新行波解，该方法可用于求解其它某些非线性偏微分方程的新解，例如 Fitzhugh-Nagumo 方程 ut− uxx=u(1 − u)(u − a), − 1 ≤ a ≤ 1．其次，进一步运用一维sine-Gordon 方程的新解、简化的变换形式(10),(11)和(12)结合广义正余弦函数法(16)找到了KdV 方程(17)的许多新行波解，类似地该方法可用于求解其它某些非线性偏微分方程的新解，例如BBM 方程ut+ux+uux−uxxt=0．最后，探求Riccati 方程、一维sine-Gordon 方程和KdV 方程(17)的更多新解及其应用值得以后进一步研究和深思．