一类非奇异H矩阵的新判据

刘长太, 徐 静, 徐辉军

(1- 扬州工业职业技术学院基础部，扬州 225127; 2- 贵州民族大学理学院，贵阳 550025)

1 引言

非奇异H 矩阵在经济数学和控制论等诸多领域都有着非常重要的应用价值[1]．设矩阵

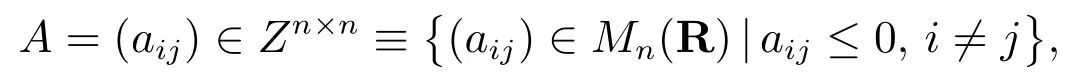
满足 B = sI − A ≥ 0 和 s > ρ(B)，则称矩阵 A 为非奇异 M 矩阵．如果 A = (aij) ∈Mn(C)的比较矩阵是非奇异M 矩阵，则称矩阵A 为非奇异H 矩阵，记作A ∈．

如果矩阵A=(aij)∈Mn(C)的每一行皆为严格对角占优的，则称矩阵A 为严格对角占优矩阵，记作A ∈D；若存在正对角阵X，使得AX ∈D，则称A 为广义严格对角占优矩阵．广义严格对角占优矩阵等价于非奇异H 矩阵[1]．

设矩阵A=(aij)∈Mn(C)，并且记

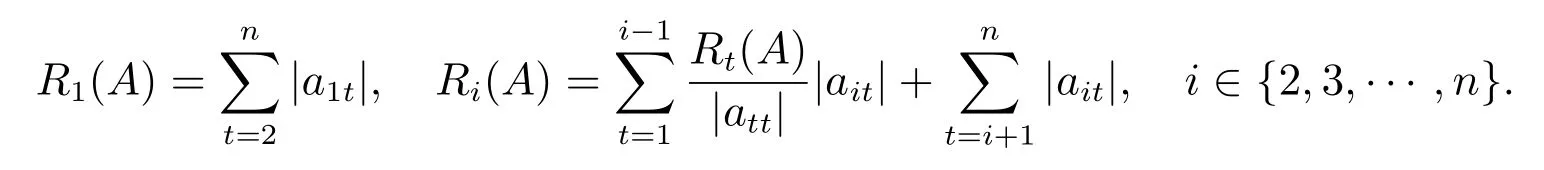
若对任意的 i ∈ ⟨n⟩ = {1,2,··· ,n}，有 |aii| > Ri(A)，则称矩阵 A 为 Nekrasov 矩阵；若存在正对角阵X，使得AX 为Nekrasov 矩阵，则称A 为广义Nekrasov 矩阵[2]．广义Nekrasov 矩阵等价于广义严格对角占优矩阵[2]．

非奇异H 矩阵和广义Nekrasov 矩阵以及广义严格对角占优矩阵皆记作A ∈ D．用迭代法求解大型稀疏线性方程组时，为了迭代收敛，常常要求迭代矩阵是非奇异H 矩阵，因此非奇异H 矩阵的充分条件为研究者所一直关注的课题，许多学者进行了深入而透彻的研究，给出了许多简捷实用的充分条件[2-8]．

2 符号与引理

设A=(aij)∈Mn(C)．记

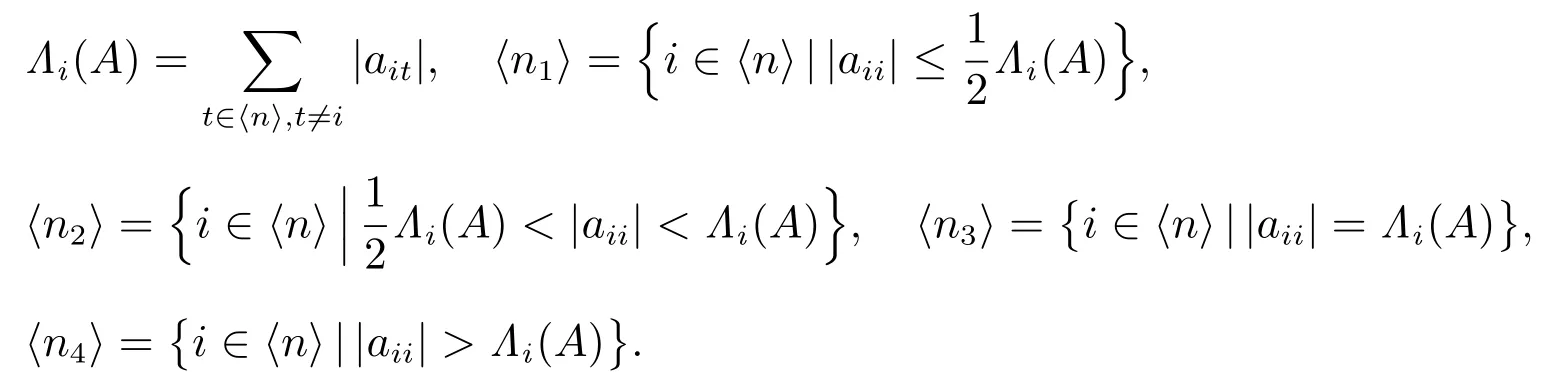
下面的结论和引理与本文的讨论是相关的：

1) 广义严格对角占优矩阵的每一个对角元皆不为零[3]；

2) 矩阵A = (aij) ∈Mn(C)每一个对角元皆不为零，记α = {i|Λi(A) > 0}，则矩阵A 为广义严格对角占优矩阵等价于矩阵A[α]为广义严格对角占优矩阵[3]；

引理1若A 为不可约对角占优矩阵，则A 为非奇异H 矩阵[3]．

引理2若A 为非零元素链对角占优矩阵，则A 为非奇异H 矩阵[3]．

引理3若A 为非奇异H 矩阵，P 为任意置换矩阵，则PTAP 为非奇异H 矩阵[9]．

因此，我们假定所讨论的矩阵 A 首先满足：对任意的 i ∈ ⟨n⟩|aii|Λi(A)>0 和 ⟨n4⟩∅．另一方面，本文中定理的条件主要是针对i ∈ ⟨n1⟩的，故还总假定：⟨n1⟩∅．规定∑t∈∅|ait|=0．为了改进和推广文献[3]，先回顾其主要结论：

定理A设A=(aij)∈Mn(C)．若对任意的i ∈⟨n1⟩，有

对任意的 i ∈ ⟨n2⟩，有

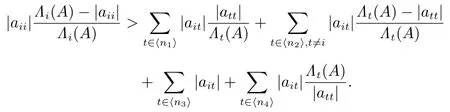
对任意的 i ∈ ⟨n3⟩，有

为了改进和推广上述结论，取k 为正整数，并且引进下列记号：

进一步地，令

3 主要结果

定理1设A=(aij)∈Mn(C)．若存在k ≥1，使得矩阵A 满足下列条件：

1) 对任意的 i ∈ ⟨n1⟩，有

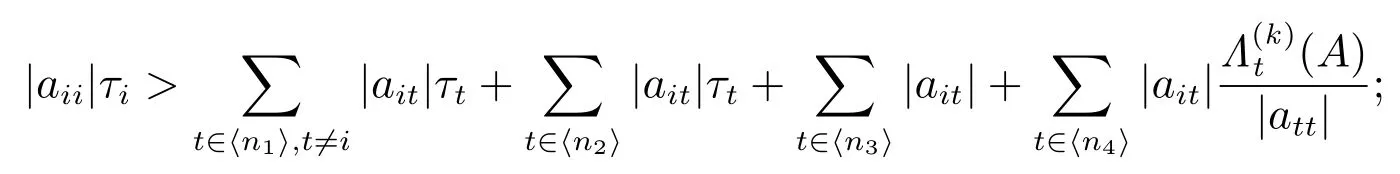
2) 对任意的 i ∈ ⟨n2⟩，有

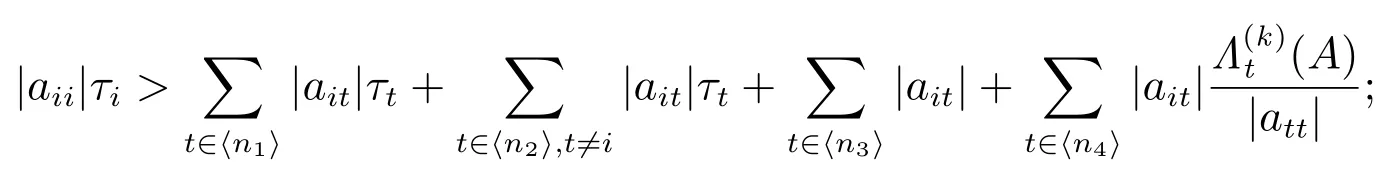
3) 对任意的 i ∈ ⟨n3⟩，有

证明 易得0 ≤r <1．

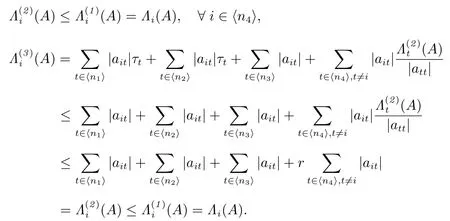
易得

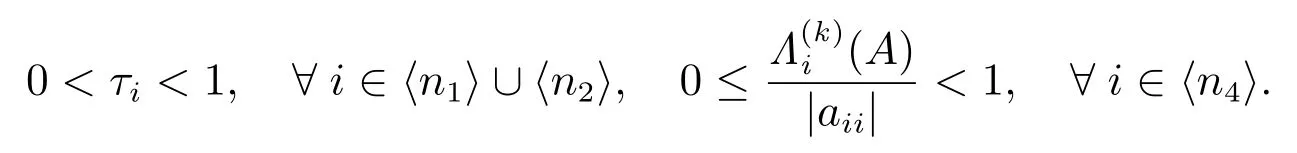
再由定理的条件可知，存在充分小的ε>0，使得下列结论皆成立：

1) 对任意的 i ∈ ⟨n1⟩，有

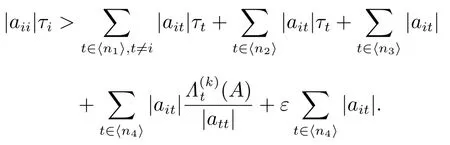
2) 对任意的 i ∈ ⟨n2⟩，有

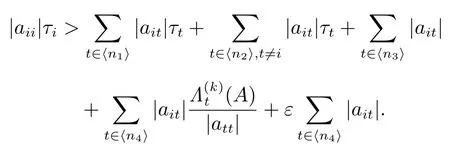
3) 对任意的 i ∈ ⟨n4⟩，有

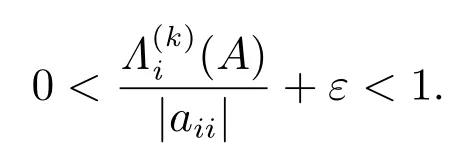
构造正对角矩阵 Y ≡ diag(y1,y2,··· ,yn)，其中

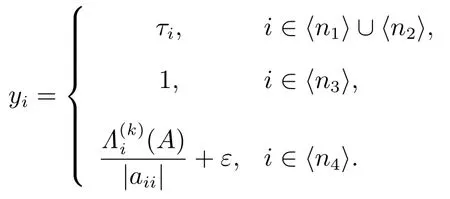
令B =( bij)=AY ，则bij=aijyj(i,j ∈ ⟨n⟩)．

对任意的 i ∈ ⟨n1⟩，有

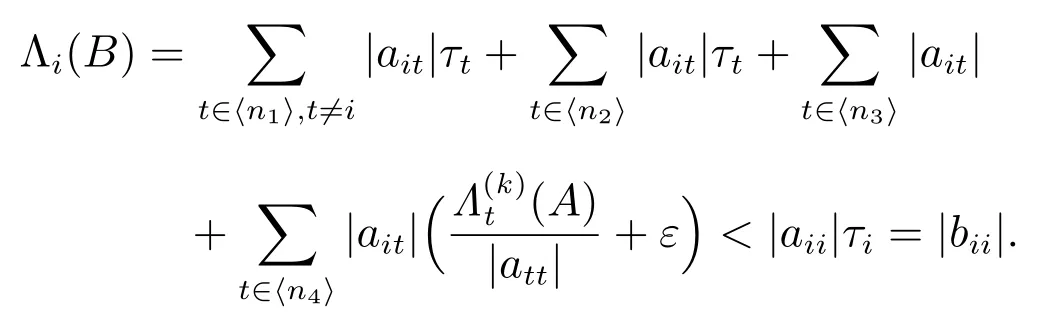
对任意的 i ∈ ⟨n2⟩，有

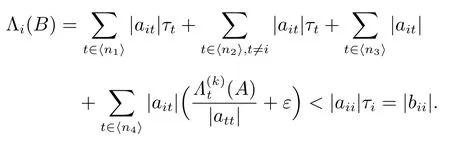
对任意的 i ∈ ⟨n3⟩，有

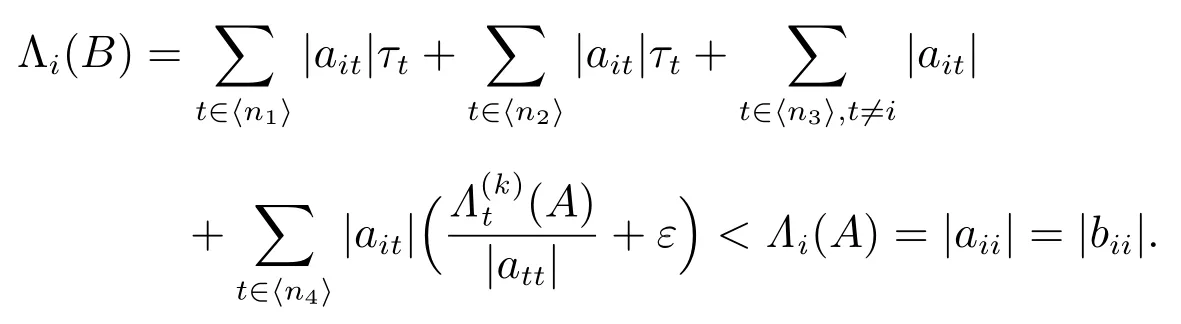
对任意的i ∈ ⟨n4⟩且k =1，有

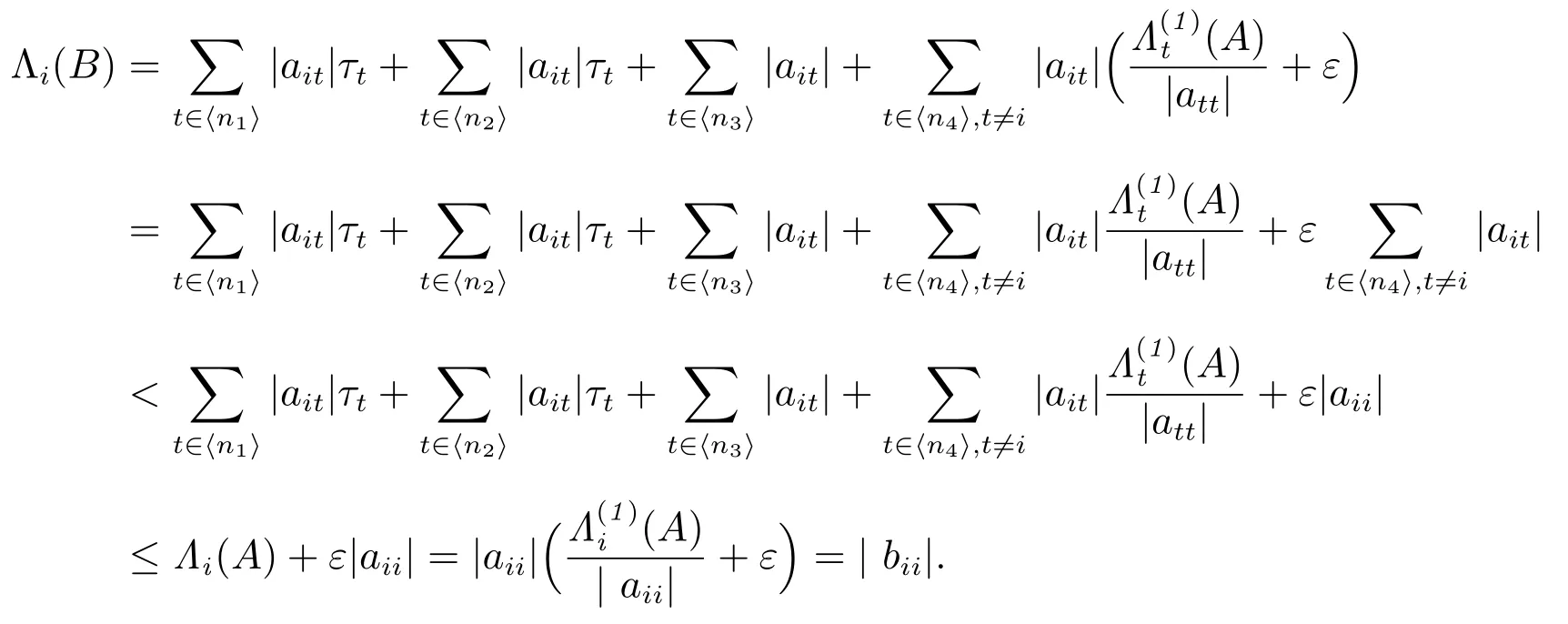
对任意的i ∈ ⟨n4⟩且k =2，有

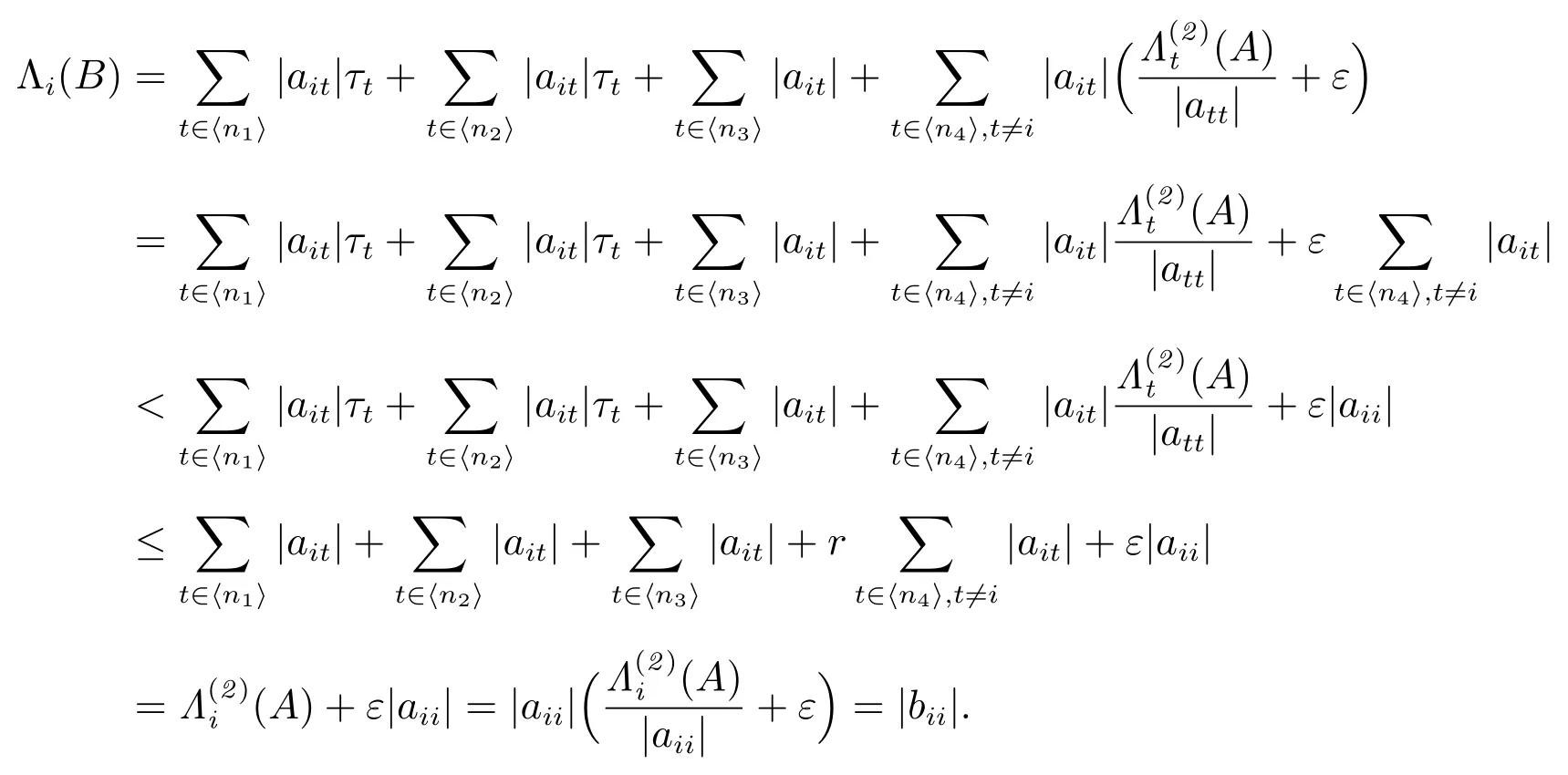
对任意的i ∈ ⟨n4⟩且k ≥ 3，有

注1对任意的i ∈ ⟨n4⟩，有故文献[3]的定理1 就是本文定理1 在k = 1 时的情形．在k > 1 时，本文定理1 的条件弱于文献[3]的定理1 的条件，因此，本文定理1 推广并改进了文献[3]中的主要结果．另一方面，定理1 的迭代形式的充分条件还可以利用下列算法实现计算机判别：

给定矩阵A=( aij)∈Mn(C)，迭代次数T：

步骤1定理1 的条件3)不满足，转入步骤5；

步骤2k :=1，定理1 的条件1)和2)满足，转入步骤6；

步骤3k :=k+1，定理1 的条件1)和2)满足，转入步骤6；

步骤4k ≤T，转入步骤3；

步骤5得出无法判定，停止；

步骤6得出A ∈，停止．

注2设矩阵A 满足定理1 的全部条件．如果矩阵A 还满足

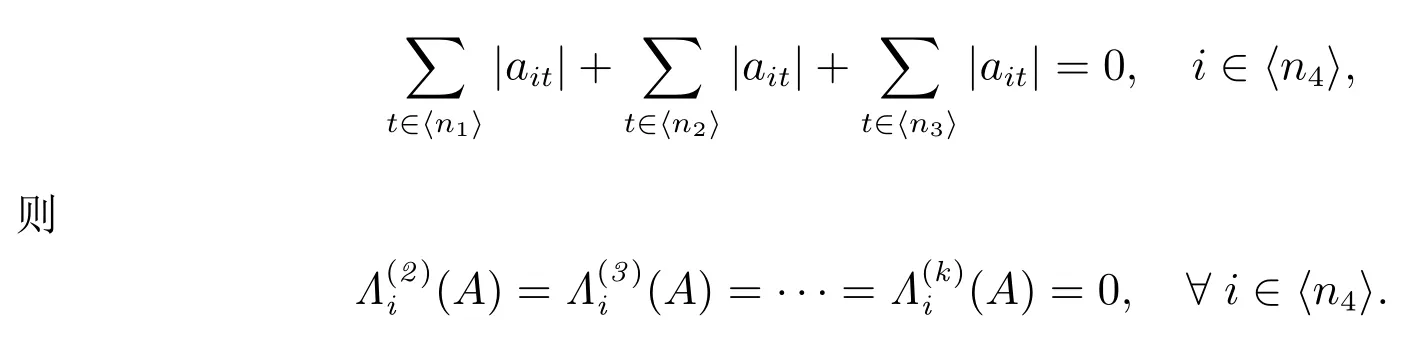
在这种情形下，定理1 的条件1)等价于

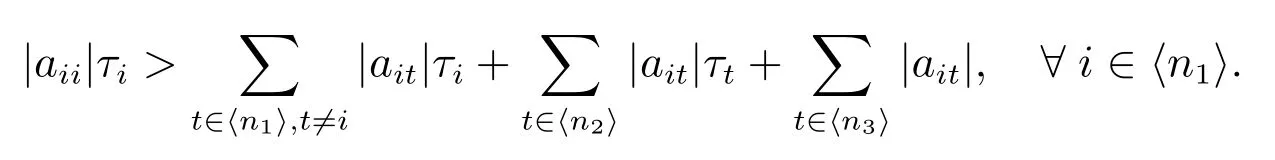
定理1 的条件2)等价于

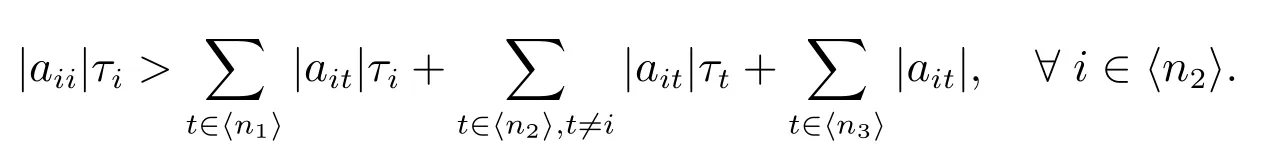
还有其它的充分条件也具有这个性质，下面的定理2 进一步说明这种现象．

定理2设A=(aij)∈Mn(C)．若矩阵A 满足下列条件：

1) 对任意的 i ∈ ⟨n1⟩，有

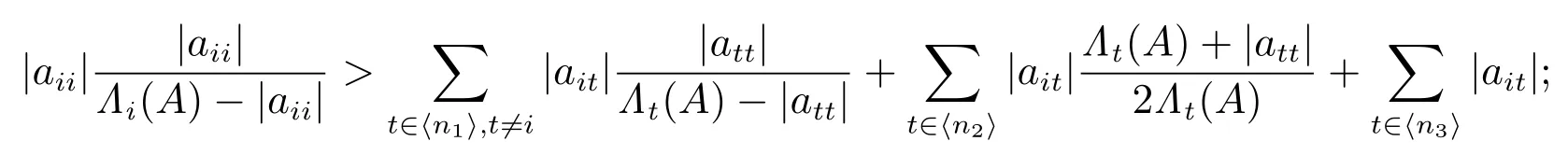
2) 对任意的 i ∈ ⟨n2⟩，有

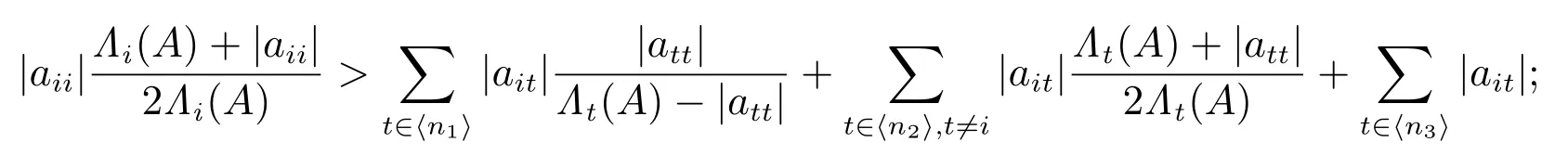
3) 对任意的 i ∈ ⟨n3⟩，有

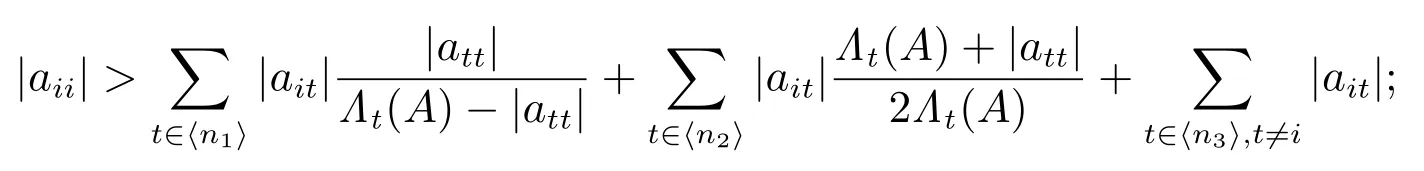
4) 对任意的 i ∈ ⟨n4⟩，有

证明 由定理的条件可知，存在充分小的ε>0，使得下列结论皆成立：

1) 对任意的 i ∈ ⟨n1⟩，有

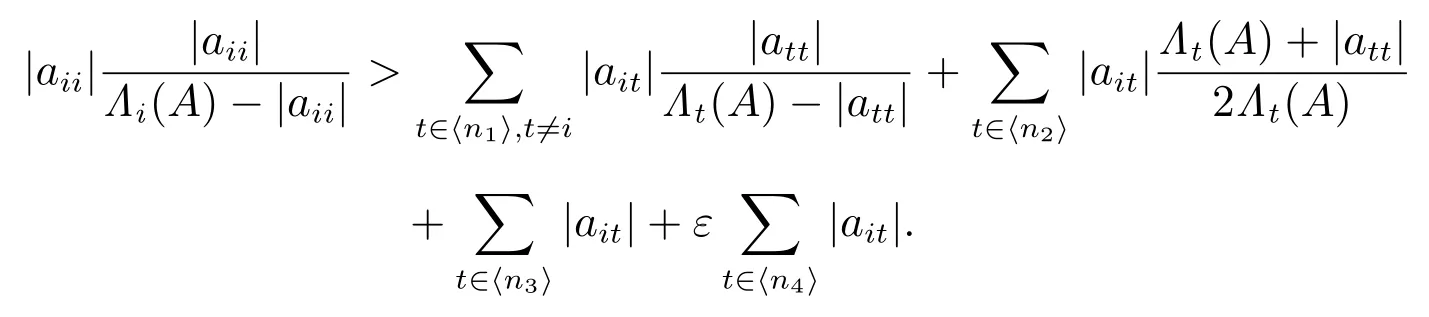
2) 对任意的 i ∈ ⟨n2⟩，有

3) 对任意的 i ∈ ⟨n3⟩，有

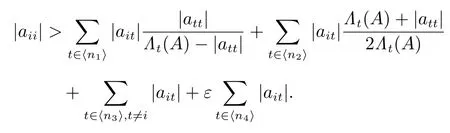
构造正对角矩阵 Y ≡ diag(y1,y2,··· ,yn)，其中

令B =(bij)=AY ，则bij=aijyj(i,j ∈ ⟨n⟩)．

对任意的 i ∈ ⟨n1⟩，有

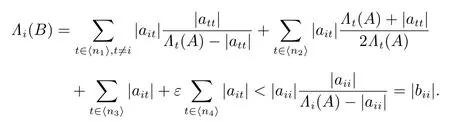
对任意的 i ∈ ⟨n2⟩，有

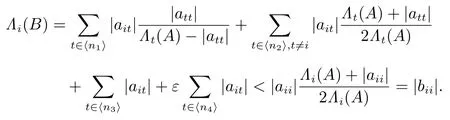
对任意的 i ∈ ⟨n3⟩，有

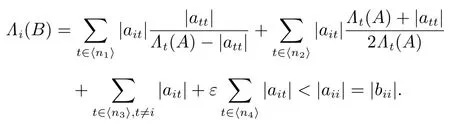
对任意的 i ∈ ⟨n4⟩，有

Taussky 的不可约对角占优矩阵和Shivakumar 与Kim Ho Chew 的非零元素链对角占优矩阵是两类重要的广义严格对角占优矩阵．定理1 在不可约和非零元素链的情形，我们有：

定理3设A=(aij)∈Mn(C)．若存在k ≥1，使得矩阵A 满足下列条件：

1) 对任意的 i ∈ ⟨n1⟩，有

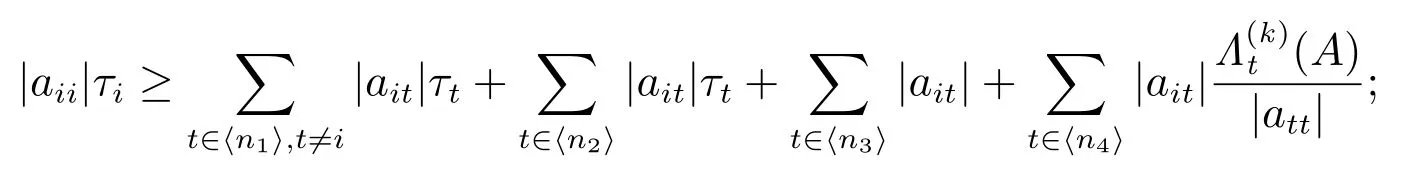
2) 对任意的 i ∈ ⟨n2⟩，有

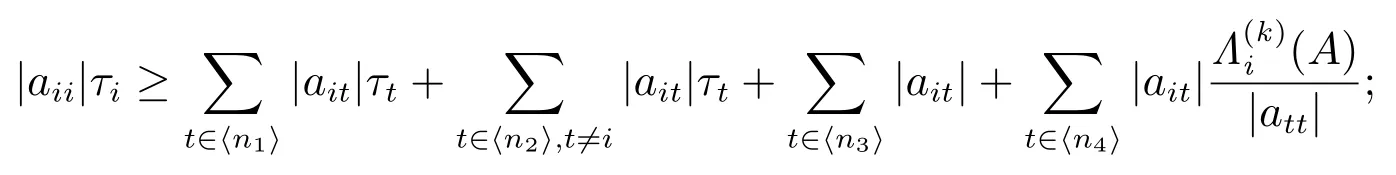
3) 对任意的 i ∈ ⟨n⟩S，矩阵 A 都有非零元素链

证明 由于对任意的 i ∈ ⟨n4⟩，矩阵 A 都有非零元素链可知

所以

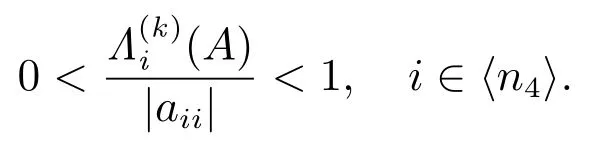
构造正对角矩阵 Y ≡ diag(y1,y2,··· ,yn)，其中

令B =( bij)=AY ，则bij=aijyj(i,j ∈ ⟨n⟩)．

对任意的i ∈ ⟨n1⟩∩ S，有

对任意的i ∈ ⟨n2⟩∩ S，有

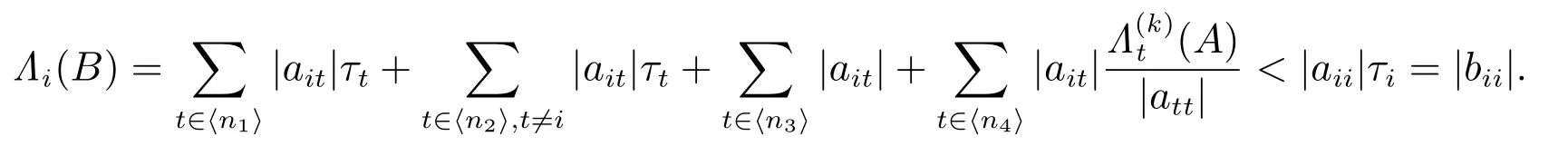
对任意的i ∈ ⟨n3⟩∩ S，有

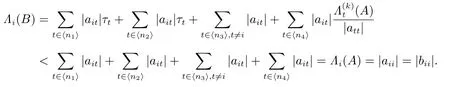
对任意的i ∈ ⟨n1⟩S，有

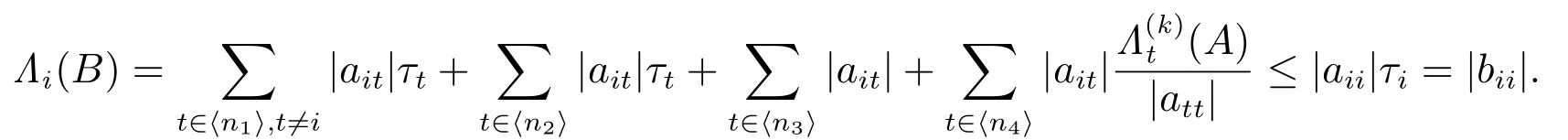
对任意的i ∈ ⟨n2⟩S，有

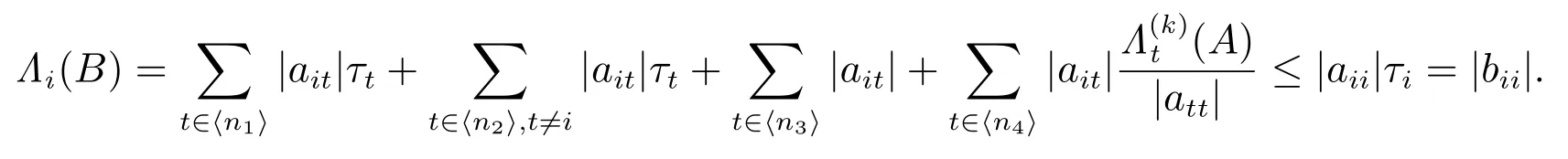
对任意的i ∈ ⟨n3⟩S，有

对任意的i ∈ ⟨n4⟩且k =1，有

对任意的i ∈ ⟨n4⟩且k =2，有

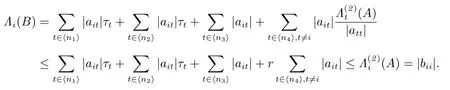
对任意的i ∈ ⟨n4⟩且k ≥ 3，有

综上所述，对任意的i ∈ ⟨n⟩S, |bii| ≥ Λi(B)且对任意的i ∈ S, |bii| > Λi(B)．另外，矩阵B 和矩阵A 具有相同的非零元素链，所以B 是非零元素链对角占优矩阵，即B ∈．进而A ∈．

推论1设A=(aij)∈Mn(C)不可约．若存在k ≥1，使得矩阵A 满足下列条件：

1) 对任意的 i ∈ ⟨n1⟩，有

2) 对任意的 i ∈ ⟨n2⟩，有

由文献[4]中定理1 可知，若矩阵A 是非奇异H 矩阵，则矩阵A 至少有一个严格占优的行．为了改进该经典的必要条件，借用定理2 的形式，可以得到下面的定理4．

定理4设 A = ( aij) ∈ Mn(C)为非奇异 H 矩阵．若⟨n1⟩∪ ⟨n2⟩∅，则下列条件至少有一个成立：

1) 若存在 i ∈ ⟨n1⟩，使得

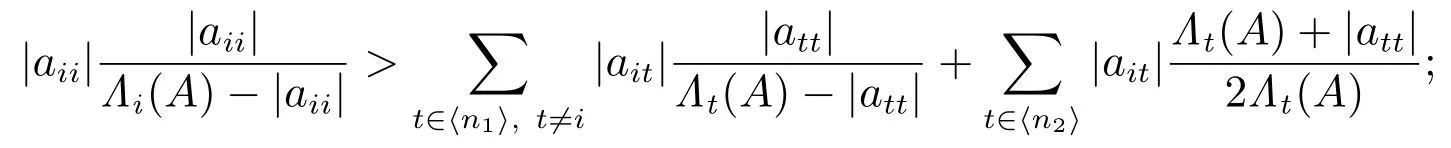
2) 若存在 i ∈ ⟨n2⟩，使得

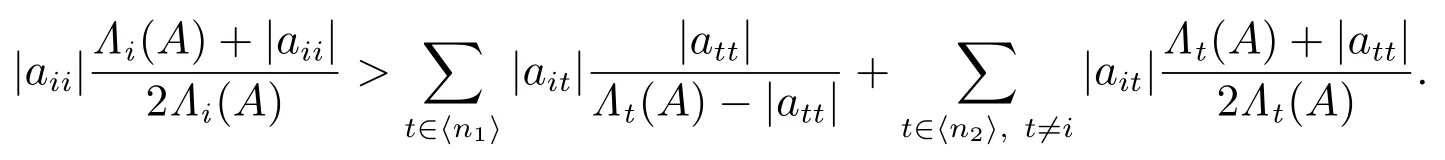
证明 构造对角矩阵Y ≡ diag(y1,y2,··· ,yn)，其中

显然Y 为正对角矩阵．令B =(bij)=AY，则bij=aijyj．

选择合适的置换矩阵P，使得PTBP 分块为

并且满足 B11=B[α]，其中 α = ⟨n1⟩∪ ⟨n2⟩．由矩阵 A 是非奇异H 矩阵和引理 3 可知

是非奇异H 矩阵，所以

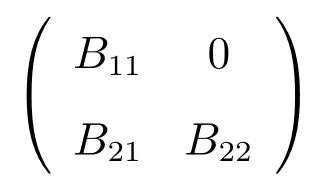
亦是非奇异H 矩阵，从而B11是非奇异H 矩阵．由文献[4]中定理1 可知B11至少有一个严格占优的行，则下列条件至少有一个成立：

1) 若存在 i ∈ ⟨n1⟩，使得

2) 若存在 i ∈ ⟨n2⟩，使得

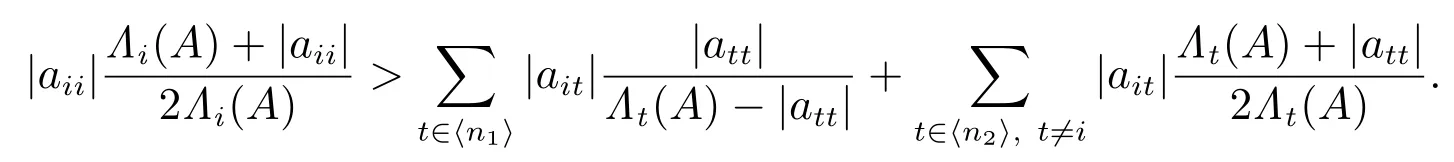
注3如果矩阵A 是非奇异 H 矩阵且满足⟨n1⟩∪ ⟨n2⟩ϕ，则定理4 中的条件 1)和条件2)至少有一个成立．所以，定理4 在一定程度上改进了非奇异H 经典的必要条件：文献[4]中定理1．

4 数值算例

例1设

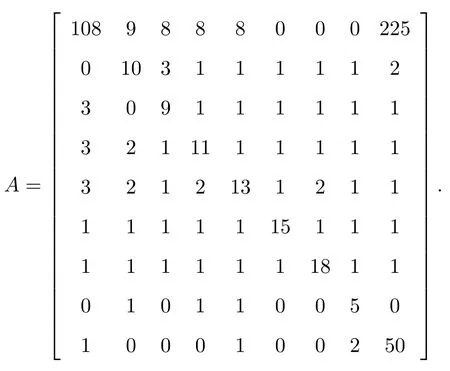
易知

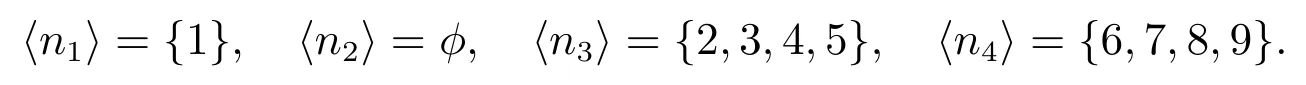
验证可知A 不满足文献[3]中的定理1 的条件，不能够判定A 为非奇异H 矩阵．

进一步验证，发现A 也不满足本文的定理1 在k = 1 和k = 2 的情形．但是，A 满足本文的定理1 在k =3 的所有条件，所以经过两次迭代就可以判定A 是非奇异H 矩阵．