双指数跳扩散模型下具有破产重组公司债券定价

林建伟, 李慧敏

(莆田学院数学与金融学院，莆田 351100)

1 引言

公司债券定价问题和最佳资本结构问题是公司金融研究的核心问题，例如Merton[1]、Black 和Cox[2]、Jones 等[3]、Leland[4]等都是在公司资产价值演化服从几何布朗运动假定下考虑公司债券定价和最优资本结构问题，但实际上公司将遇到许多不确定因素或突发事件，如金融危机、通货膨胀、自然灾害等，一旦发生，往往导致公司资产价值的剧烈震动，从而使得资产价值发生跳跃．鉴于几何布朗运动无法刻画由不确定因素引起的资产价值跳跃现象，许多学者通过不同跳扩散模型描述资产价值的演化过程，并对公司债券进行定价，研究工作包括：Zhou[5]、Chen 和Kou[6]、向华和杨招军[7]、林建伟[8]等，但是他们都视破产等同于清算，即公司一旦宣布破产，将立即被清算，不考虑破产重组．实际上，现实市场中，公司一旦宣布破产，仍有权对公司进行破产重组，以期重整旗鼓．考虑到这一点，许多学者通过破产重组的数学建模，区别破产和清算，进而考虑公司债券定价问题．研究工作包括：Anderson 和 Sundaresan[9]、Fan 和 Sundaresan[10]、Broadie 和 Kaya[11]、Dai 等[12]，但这些文献都是在公司资产价值演化服从几何布朗运动假定下获得的，不考虑公司资产价值跳跃因素．为了统一考虑资产价值发生跳跃现象和破产重组两个重要的市场因素，本文拟利用文献[6]提出的双指数跳扩散模型来刻画公司资产价值的演化过程，同时采用文献[10]提出的债券和股票互换的破产重组模式，通过结构化方法和最优停时技巧，对具有破产重组的永久公司债券进行定价，并分析最优资本结构问题．

2 基本假定和纳什均衡分配

2.1 基本假定

1) 市场无套利和市场无风险利率为常数r；

2) 公司发行股票E 与永久公司债券D，债权人在公司宣布破产前可获得每单位时间C 元的息票收益，同时公司也可获得额外税盾收益，即企业从发行公司债券中每单位时间获得税盾收益γC，γ(0<γ <1)表示企业税率；股东按红利获得收益；

3) 在等价鞅测度Q[6]下，公司资产价值Vt演化服从双指数跳扩散过程

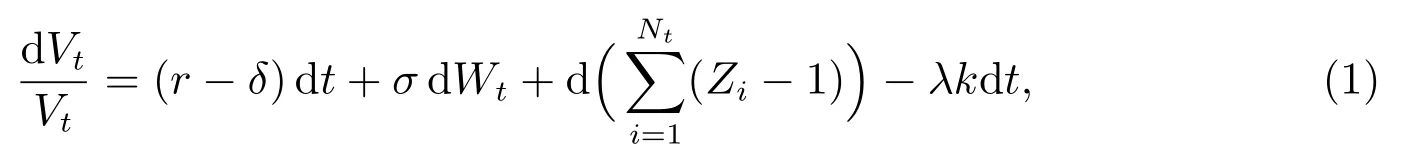
这里δ 为公司总的现金支付率，σ 为波动率，{Wt}t≥0为一个标准的Brown 运动，{Nt}t≥0表示强度为λ 的泊松过程，随机变量{Z1,Z2,···}独立同分布，且假定{Wt}t≥0，{Nt}t≥0和Zi在等价鞅测度Q 之下相互独立．k 表示平均跳跃比例，即

其中Yi=ln(Zi)服从双指数分布，即具有如下的密度函数

且pu>0, pd>0, pu+pd=1，两者分别表示向上跳和向下跳的概率；

4) 最佳破产边界的选取标准：股票价值最大化；

5) 清算损失率为α(0<α<1)；

6) 破产重组模式—股票债券互换模式[10]：当公司宣布破产时，公司首先将债权人持有的债券等价转化为相当份额的股票，使得公司转化为全股票公司，并向投资者出售，获得破产时刻公司的资产价值，由此避免直接清算而造成的资产价值损失；然后对获得的破产时刻公司的资产价值进行重组，并通过纳什均衡原理确定股东和债权人各自的最佳重组比例．

2.2 纳什均衡分配

在任一给定公司宣布破产时刻τ，相应的公司资产价值为Vτ，若公司没有选择进行破产重组，则公司将直接被清算，导致公司损失资产价值αVτ，即此时股票价值为零，债券的价值为(1 −α)Vτ；但是若公司选择进行破产重组，由基本假定6)，公司根据股票债券互换模式对破产时刻公司的资产价值Vτ进行重组，即权益双方的价值为

这里θ 为股东的分配比例．通过纳什均衡分配原理，最佳分配比例θ∗确定为

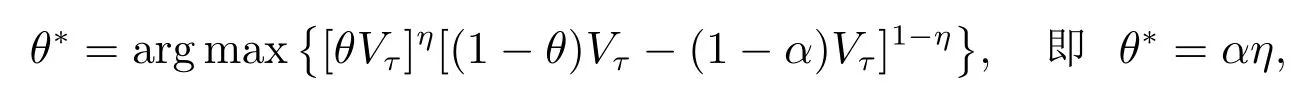
其中η(0 ≤η ≤1)表示股东的谈判能力．综上，在任一给定公司宣布破产时刻τ，股票和债券的价值为

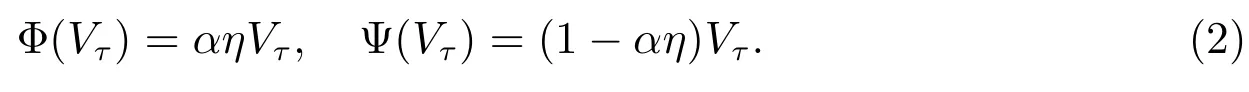
3 公司股票价值的定价公式

对于任意公司宣布破产时刻(停时)τ，基于模型的基本假定，在等价鞅测度Q 下，股票价值E 的定价模型为

这里T[t,∞]表示发生在[t,∞]上所有停时的集合．等式(3)右边第一项表示公司宣布破产之前股东红利收益的贴现值，第二项表示破产时刻通过重组股东获得收益的贴现值．

利用动态规划原理，股票定价的数学模型(3)等价于如下变分不等式方程

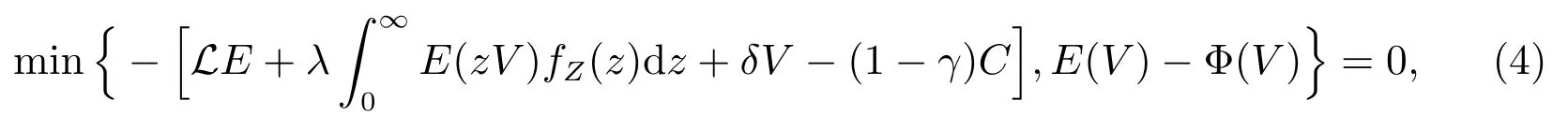
且满足边界条件

这里fZ(z)表示Z 的密度函数

根据变分不等式的性质，上述股票价值满足的变分不等式方程转化为如下自由边界问题。问题P1：求{E(V),V∗}满足

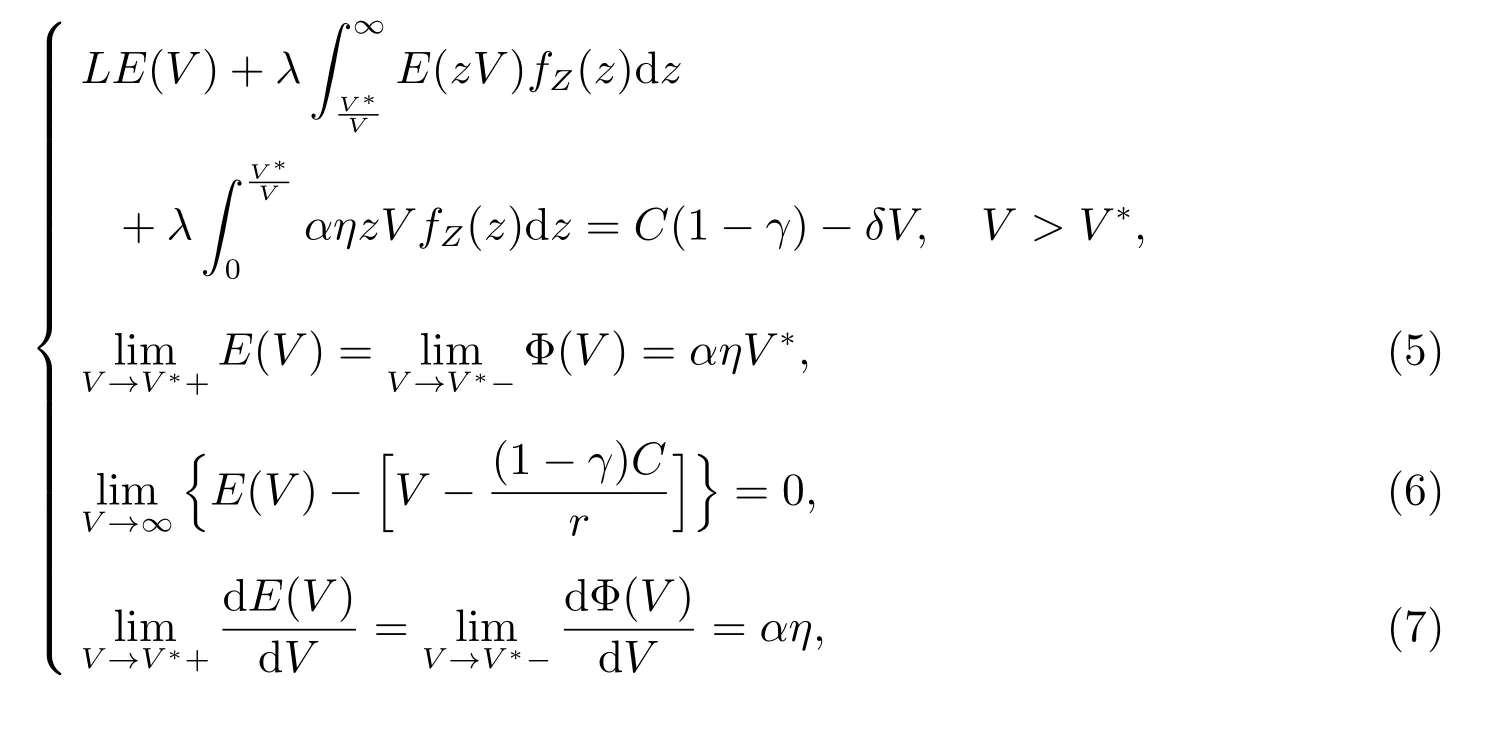
这里V∗表示公司最佳的破产边界点．

边界条件(5)式说明，在破产时刻，通过破产重组，股东可获得αηV∗；而(6)式表示，当公司资产价值趋于无穷大时，公司债券转化为一张无风险公司债券，其价值为股票价值为公司资产价值V 加上税盾收益减去无风险公司债券的价值条件(7)表示金融上的一个光滑接触条件，即选取最佳破产边界点V∗使得股东权益最大化．

作变换

这里

对定解问题P2 进行求解，并返回原变量，可得如下定理．

定理1当V ≥V∗时，公司的最佳破产边界点V∗和股票价值E(V)的表达式为

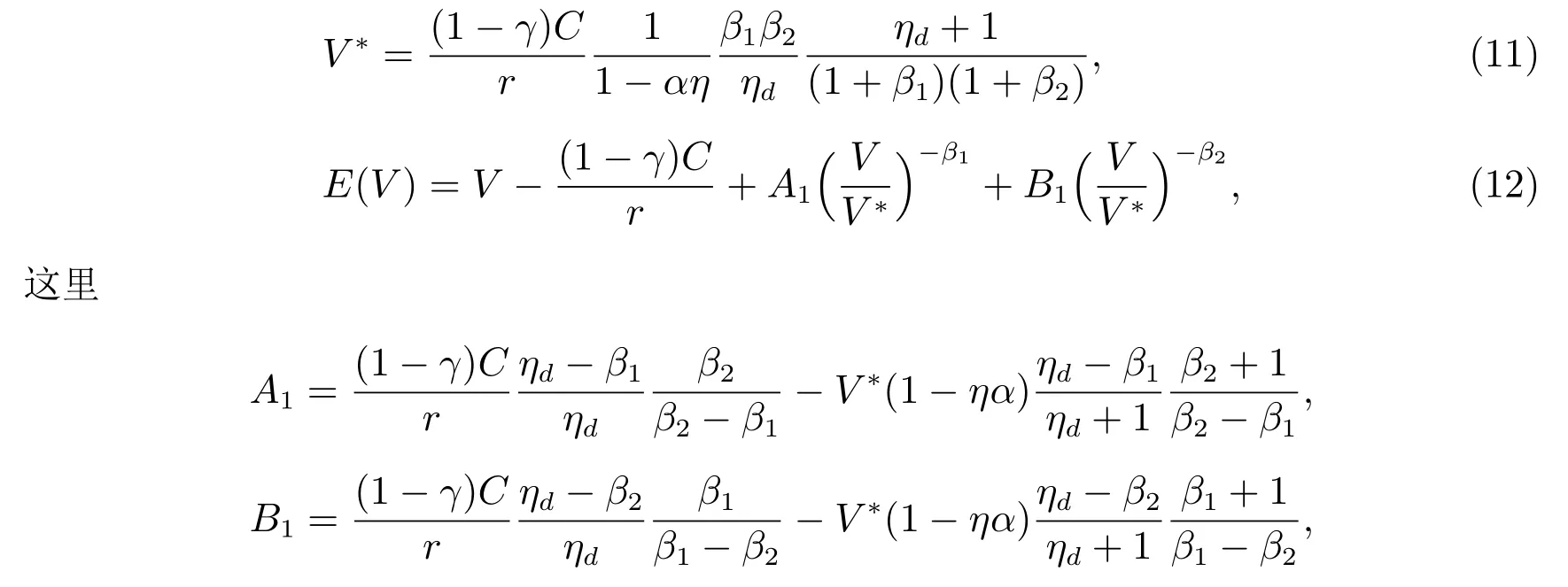
β1, β2为方程G(β)=r 的两根，且满足0< β1< ηd< β2< ∞，这里

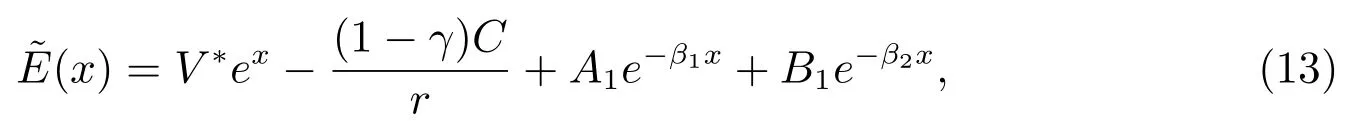
这里A1, B1为待定的常数，β1, β2为方程G(β) = r 的两根，且满足0 < β1< ηd< β2<∞，其中

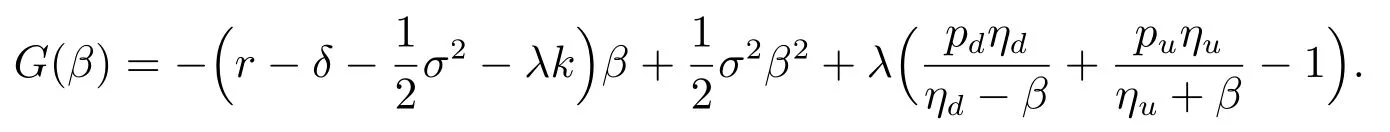
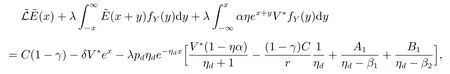
由边界条件(8)，可得

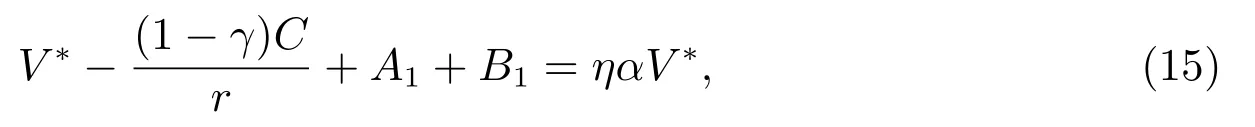
联立(14)和(15)，A1和B1确定如下

最后，利用光滑接触边界条件(10)，可得

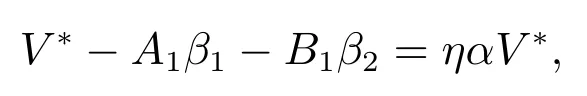
经过计算，可得最佳破产边界V∗解的表达式为

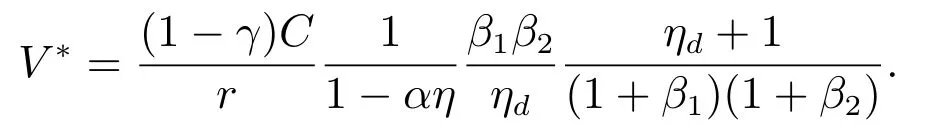
4 永久公司债券的定价公式

基于最佳破产边界点V∗，定义停时τ∗=inf{s ≥t:Vs≤V∗}，表示公司资产价值首次碰到最佳破产边界的时刻．在等价鞅测度Q 下，永久公司债券的定价模型为

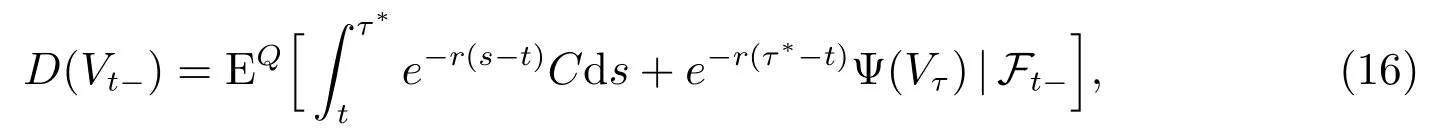
等式(16)右边第一项表示公司宣布破产之前债权人获得的总息票收益贴现值，第二项表示破产时刻通过破产重组债权人获得收益的贴现值．

基于公司债券的数学模型(16)，通过动态规划原理，可得到永久公司债券满足定解问题Q1：

边界条件(17)式表示，破产时刻债权人从破产重组中获得(1 −αη)V∗收益；而(18)式表明，当公司资产趋于无穷大时，公司债券转化为一张无风险公司债券，其价值为

作变换

问题Q1 转化为问题Q2：

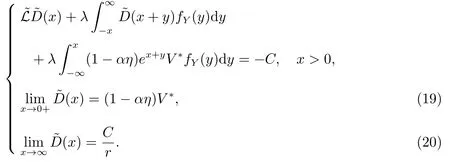
对于定解问题Q2 进行求解，返回原变量，并结合公司总价值v(V) = E(V) +D(V)，可得如下定理．

定理2当V ≥V∗时，公司总价值v(V)和公司债券价值D(V)的表达式为

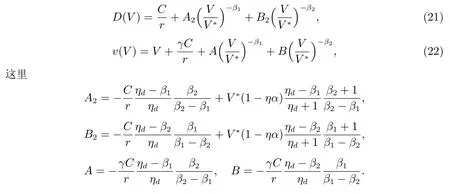
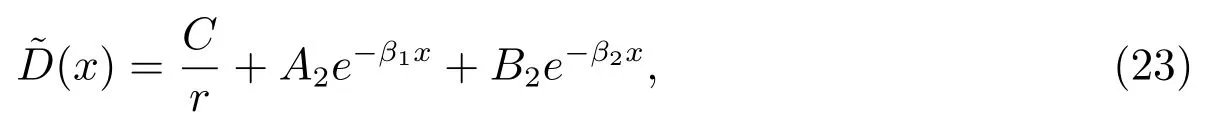
这里A2, B2为待定的常数．

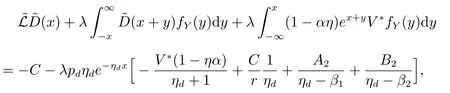
由边界条件(19)，可得

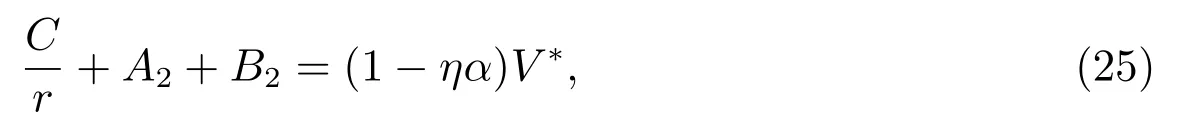
联立(24)和(25)，A2和B2确定如下

最后，基于v(V) = E(V)+D(V)，结合(12)和(21)，即可获得公司总价值v(V)解的显式表达式(22)和相应的系数A, B 的表达式．

5 公司的最优息票

公司一方面通过发行债券每单位时间可以获得税盾收益γC，但另一方面每单位时间公司需要向债权人支付息票C，使得公司面临的破产风险增大，因此如何权衡公司的杠杆比例是至关重要的．这里主要通过选取最优息票C∗，使得公司总价值v 最大而确定公司最优的杠杆比例．

基于公司总价值的表达式(22)，将公司总价值v(V)看成息票C 的函数，选取最优息票C∗，使得

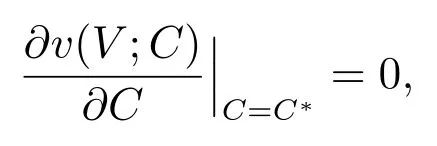
可得如下定理．

定理3公司的最优息票C∗满足非线性方程如下

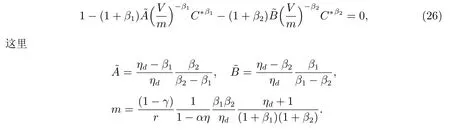
6 金融意义分析

基于获得的定价结果(11),(12)和(21),(22),(26)，在最优息票C∗下，观察股票价值、债券价值和公司总价值关于跳跃强度λ 的依赖关系，并与Fan 和Sundaresan(FS)模型(在公司资产价值演化服从标准几何布朗运动下，对具有股票和债券互换破产重组公司债券进行定价)相应的定价结果做比较，分析跳跃强度所引发的金融现象．基本参数可设定为

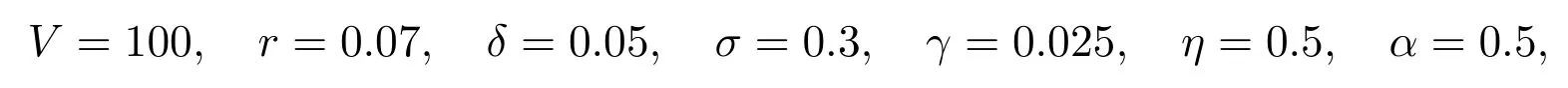
上跳概率pu=0.25，下跳概率pd=0.75，平均上跳幅度平均下跳幅度发生跳跃强度λ=1(表示平均每年公司资产价值发生一次跳跃)．

图1 表明，在最优息票C∗下，股票价值随着跳跃强度增大而增大，且相比于FS 模型，当跳跃强度充分大时，在跳扩散模型下股票价值更大，而当跳跃强度比较小时，股票价值趋近于FS 模型里的股票价值．其金融意义为：当公司资产价值变化越剧烈，股东越能在动荡的市场环境中获益，相应的股票价值越大；但当市场趋于平稳时，股票价值随之下跌．

图1: 最优息票C∗下，股票价值E(V)关于λ 的变化关系

图2 和图3 表明，在最优息票C∗下，债券价值和公司总价值随着跳跃强度增大而减小，且相比于FS 模型，在跳扩散模型下债券价值和公司总价值均更小．其金融意义为：当公司资产价值变化越剧烈，市场环境越动荡，债券越不受投资者青睐，债券价值越低，导致公司总价值也越低，即公司债券的融资规模越小；但当市场趋于平稳时，债券价值上涨，公司债券的融资规模增大．

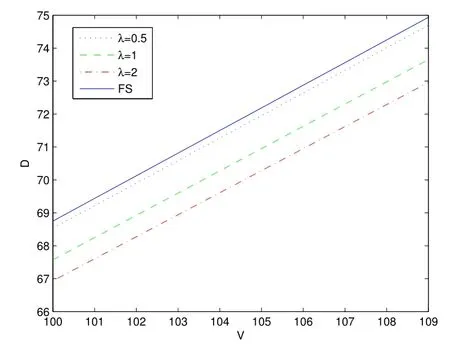
图2: 最优息票C∗下，股票价值D(V)关于λ 的变化关系

图3: 最优息票C∗下，公司总价值v(V)关于λ 的变化关系

图4 表明，在最优杠杆比例L(最优杠杆比例L 等于在最优息票C∗下公司债券价值占公司总价值的比例)是跳跃强度的减函数，且相比于FS 模型，在跳扩散模型下最优杠杆比例更低．其金融意义为：在跳扩散模型下，公司资产价值变化更加剧烈，市场环境更加动荡，债券受投资者的青睐程度降低，因此相应的杠杆比例也更低．

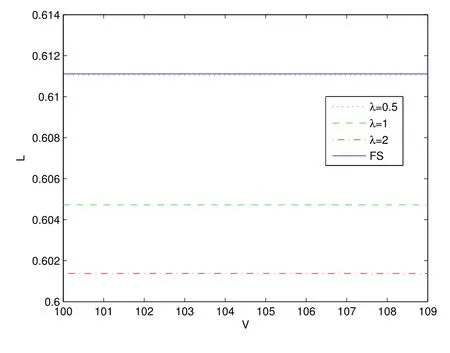
图4: 最优息票C∗下，最优杠杆比例L 关于λ 的变化关系

7 结束语

本文在双指数跳扩散模型下，基于债券和股票互换的破产重组模式，采用结构化方法和最优停时技巧建立了永久公司债券、股票定价的数学模型，并通过微分方程方法，获得了永久公司债券、股票定价以及相应最佳破产边界的显式表达式，并以公司总价值达到最大值为优化标准，获得了最优息票所满足的非线性方程．数值分析表明：在最优息票C∗条件下，公司资产价值震荡越剧烈，股东越能从动荡的市场中获得收益，且相比于FS 模型，当跳跃强度较大时，跳风险下股票价值更大，当跳跃强度较小时，跳风险下股票价值趋近于FS 模型中股票价值．不同于股票价值，当市场环境越动荡，公司债券将越不受投资者青睐，公司债券价值越低，公司债券融资规模越小，最优杠杆比例越低；而当市场环境趋于平稳时，公司债券价值增大，公司债券融资规模增大，最优杠杆比例增大，且相比于FS 模型，跳风险下公司债券价值，公司融资规模和最优杠杆比例都更小．