二阶随机占优约束下考虑订购能力的多产品报童问题

付永彬, 孙海琳

(南京师范大学数学科学学院，南京 210023)

1 引言

经典报童问题即单周期库存问题(Single-Period Problem, SPP)，其研究对象为生命周期短、易腐蚀、订货机会只有一次的产品，主要研究其订货问题和库存决策问题，是供应链管理中最重要的模型之一．随着生产和销售的复杂化，学者们将经典的报童模型扩展为多产品报童模型(Multi-Product Newsvendor Problem, MPNP)，通过在各种产品之间合理分配有限的资源，使报童总的期望利润最大或损失最小．

Whitin[1]首次建立了受价格影响的报童模型；Khouja[2]对报童问题的扩展模型做了分类说明；Mitra[3]以单产品报童问题为背景，将产品的残值、清仓价格均视为决策变量，分别就季节性需求和季末需求是否外生和随机建立了三个模型．Kyparisis 和Koulamas[4]分析了非负线性可加需求对单产品报童问题订价敏感度的影响．Wu 等[5]研究了单产品的报童博弈问题，提出了两种数量竞争的需求分割规则，包括需求分配比例规则和需求再分配规则．Wang 等[6]考虑单产品报童模型，分别对风险中性和风险厌恶下随机供应对最优订货量的影响进行了研究．Mohammad 和Shokri[7]考虑风险厌恶条件下，以CVaR 为风险度量的多产品选择问题．Farahat 和Leeb[8]考虑在一般选择规范下，即包含替代、互补、多单位订购、缺货、库存等情形，建立了客户的对产品选择模型．Shi 等[9]讨论了供应商数量折扣合同下，多产品多约束的联合订价及最优订购量问题；Murray 等[10]主要研究在资源能力有限条件下，报童的多产品订价问题；周继祥[11]分别讨论了订货无约束下、供应商随机生产约束下、资金约束下报童模型的显式解；陈杰等[12]对具有多元马氏需求特征的多产品库存报童模型的优化问题进行了探讨；Ma 等[13]针对需求可替代的多产品报童问题研究了其最优产品组合及最优订货量的联合决策问题．

在现实中大多数零售商是风险厌恶的，针对需求的不确定性所带来的风险，许多学者采用不同的模型进行研究．张艳霞等[14]对定常风险下具有不同风险偏好组合决策者的报童问题进行了风险分析；简惠云和许民利[15]针对风险规避和风险偏爱两种情况，分别建立不同订购量和风险水平下的条件风险值模型，考虑缺货成本，在一定条件下，得到任意风险水平下的VaR 解析表达式；周艳菊等[16]运用前景理论，针对需求不确定条件下的两产品订货问题进行了分析；Zhang 等[17]分别采用VaR 和CVaR 对单周期和多周期报童问题进行建模．

随机占优(Stochastic Dominance, SD)是风险管理的一种理论方法，已经广泛用于经济、管理学和金融学领域．Hadar 和Russel[18]首次提出随机占优的理念；Fishburn[19]整理出随机占优理论，并将随机占优理论应用于组合投资问题．作为一种重要的随机占优方法，SSD 可用来描述风险规避型投资者的行为．Dentcheva 和Ruszczyski[20]首次提出带有SSD 约束的随机优化模型，他们通过引入新的变量把该问题重新构造成一个线性约束优化问题；Dentcheva 和Ruszczyski[21]分析了该问题的最优性与对偶性等问题；Homem-De-Mello 和Mehrotra[22]结合了割曲面算法与样本均值逼近(SAA)方法来求解带SSD 约束的随机优化问题；Sun 等[23]用光滑的罚函数SAA 方法来求解该问题；Rudolf 和Ruszczyski[24]，Fbin 等[25]分别采用切平面算法来求解带SSD 约束的随机优化问题；Sun 等[26]进一步将切平面法改进，更适宜解决大量非线性约束的凸优化问题；Yang 等[27]将SSD 应用于供应链系统，研究了多制造商多零售商之间最大化利润的交叉订购与定价问题；罗晓琴等[28]将二阶随机占优理论应用于保险资金资产组合优化；吴敏等[29]考虑偏度因素，建立了SSD 约束下最大化组合收益率偏度的投资组合优化模型；张宏伟等[30]采用SSD 理论对投资组合问题进行建模，并通过遗传算法求解；杨柳和申飞飞[31]通过引入交易费用函数，建立带有SSD 约束的投资组合风险控制模型．

在随机规划问题中，随机变量未知．SAA 是一种经典的、实用的估计随机变量分布的方法．该方法利用随机变量的经验分布去近似其真实分布，有着深厚的理论基础、良好的可操作性和应用价值，在学术界已被广泛论证和使用[32]．进一步，SAA 在报童问题中也是常用的方法[17]，部分原因是报童问题的零售商可以比较方便地根据以往销售情况获得产品需求的各项信息作为SAA 问题的样本．这样的样本具有真实、利用率高等优势．

多产品报童问题涉及库存管理、风险管理、供应链协调等多个领域．随着风险控制领域的不断发展，将新的风险测度应用于报童模型既能体现新的风险测度的优越性，又能对经典模型带来新的思路和启发．本文建立了带有随机二阶占优约束的多产品报童模型，主要贡献如下：

1) 本文首次将SSD 与报童问题相结合，建立了带有SSD 约束的多产品报童模型，考虑了在SSD 约束及订购能力约束下零售商的最优订购策略；

2) 本文采用SAA 方法对带有SSD 约束的多产品报童模型进行逼近，并对SAA 逼近问题进行收敛性分析；继而采用切平面法[26]对SAA 问题进行求解．数值实验的结果既验证了SAA 问题的收敛性，同时又说明了SSD 模型的优越性．

2 SSD约束下的报童模型

2.1 模型介绍及参数设定

鉴于零售商总是同时订购和销售多种产品，本文考虑对零售商在单周期内对多种产品销售的报童问题进行建模．现实中零售商往往不会把所有资金都应用于产品订购，或者出现零售商订购能力有限，或资本难以周转等其他情形，所以本文设定订购能力约束；同时又借助SSD 来规避风险．假设各种产品之间互不相关，不考虑订货提前期且货源充足．产品的零售价格由市场决定，为已知量；订购价格和残值由供应商决定，为已知量；产品市场需求为随机变量．零售商需要在销售季到来之初，确定各种产品的订购量，以期获得最大利润．

设共有M 种产品，对第m(m=1,2,··· ,M)种产品：订购量为xm, xm∈R+；市场需求为Dm, Dm: Ω → Ξm是定义在概率空间(Ω,F,P)上的随机变量，分别为单位销售价格、单位订购价格、单位残值，且pm>cm>vm>0．令

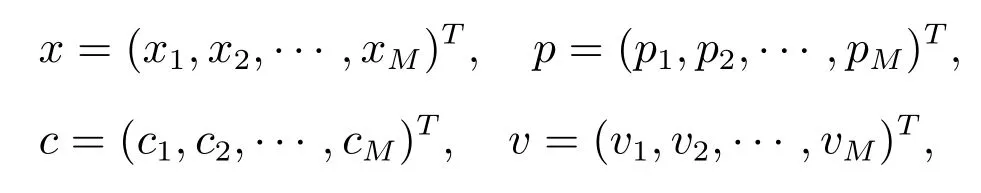
则在当期对于第m 种产品，零售商的销售量为min(xm,Dm)；库存量为xm−min(xm,Dm)；销售收入为pmmin(xm,Dm)；未卖出产品的残值为vm[xm−min(xm,Dm)]；订购成本为cmxm．所以第m 种产品的利润为

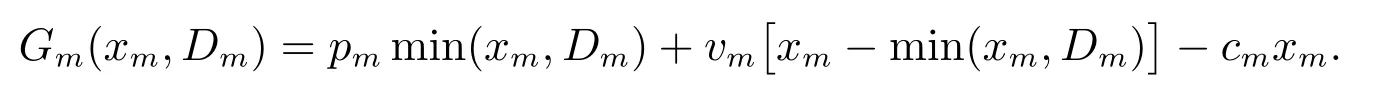
M 种产品的总利润为

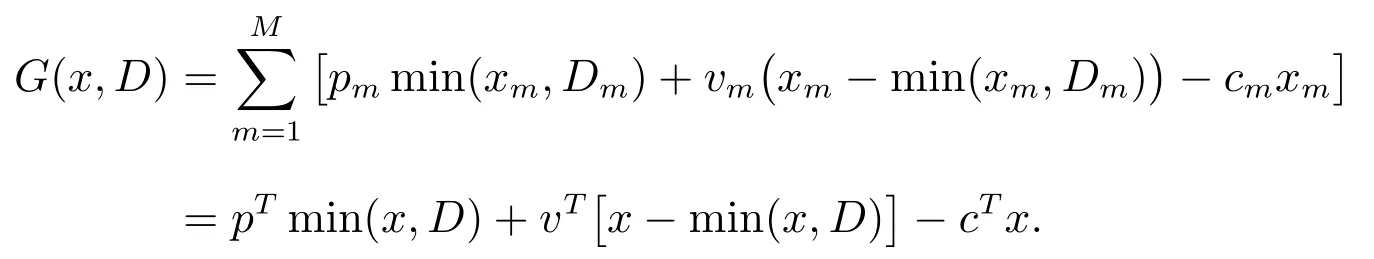
由于min(a,b)=a −(a −b)+，其中(a −b)+=max(a − b,0)，上式可化简为

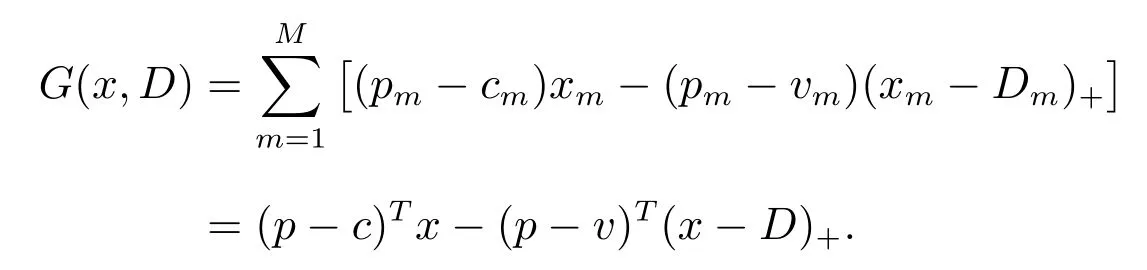
设J(x,D)=−G(x,D)表示损失函数．在订购能力约束下最小化期望损失的报童模型为

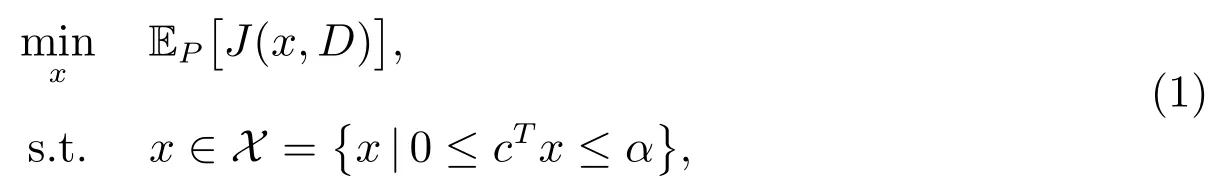
其中α 为常数，该模型也称作风险中性模型．

2.2 SSD约束下的报童模型

在现实中大部分投资者是风险厌恶的，而问题(1)未考虑风险因素对报童的影响．如前文所述SSD 可用来描述风险规避型投资者的行为，因此，本节引入SSD 约束，构建带有SSD 约束的风险规避型报童模型．

首先介绍SSD 的定义：设X(ω), Y(ω)分别为随机变量ω 的两个函数，其累积分布函数分别为FX(ω)(η)和FY(ω)(η)，即FX(ω)(η)=P(X(ω)≤ η)．令若满足

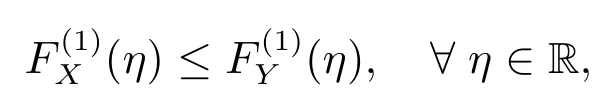
则称X(ω)一阶随机占优于Y(ω)，记作X(ω)≽1Y(ω)．令

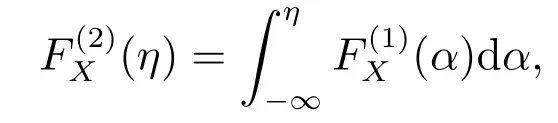
若满足

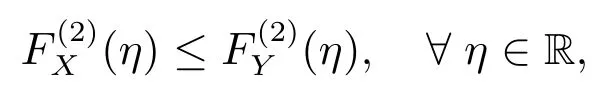
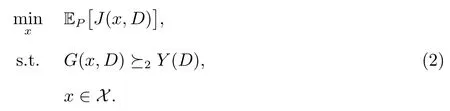
式(2)中Y(D)为基准随机变量．由SSD 性质(文献[20]中的2.6,2.7 式)，可知问题(2)等价于

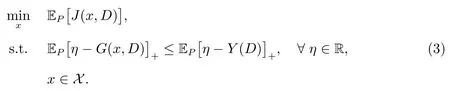
由于问题(3)不满足Slater 约束规范，所以考虑其松弛问题

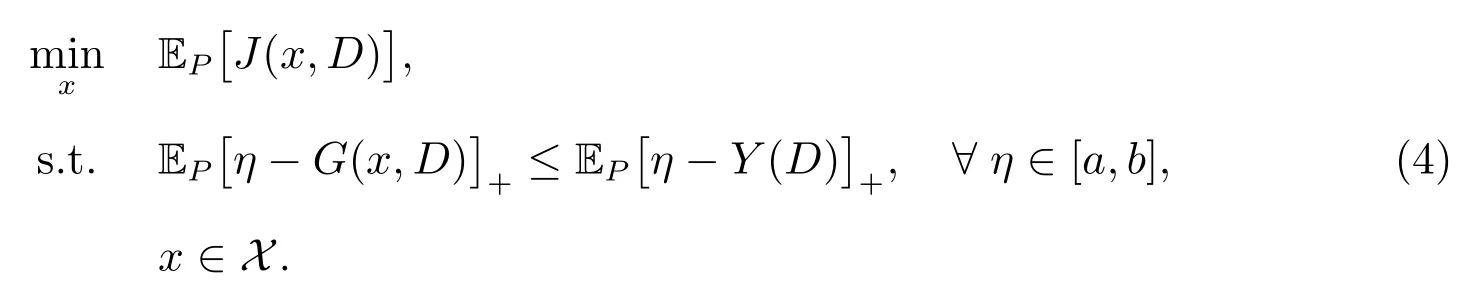
称问题(4)为真问题，这里[a,b]是R 中一个有界闭区间．

3 SAA方法及其收敛性分析

本节研究真问题(4)的SAA 问题．设随机变量D 的独立同分布样本为为方便起见，令Yi=Y(di)，则其SAA 问题为

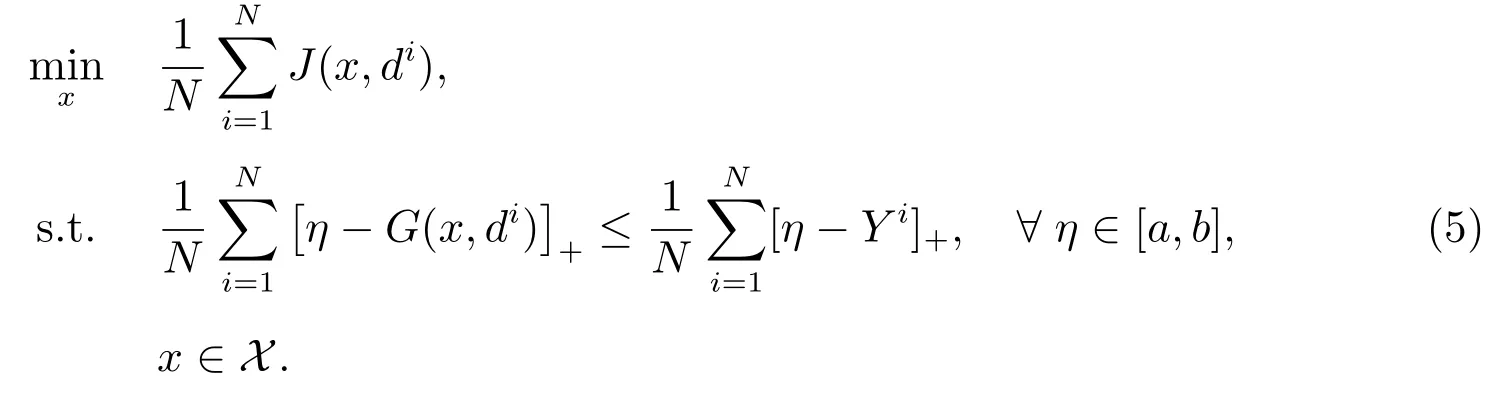
接下来给出SAA 问题(5)的收敛性分析．

3.1 几乎处处收敛

带有SSD 约束的优化问题的最优性条件已被Dentcheva 和Ruszczyski[20,21,33]证明．关于该问题的SAA 问题的收敛性在文献[23,26,34]中也给了出来．这里根据报童问题的特点，利用前述文献的结果，证明了带有SSD 约束的多产品报童问题的SAA 问题的收敛性．

为简化符号，令p(a)=max(0,a)，则有

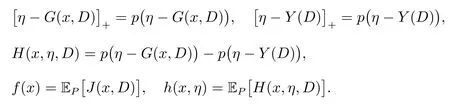
命题1假设存在点x0∈X, η0∈[a,b]，使得

那么，我们有：

(i) 对任意的x ∈ X, η ∈ [a,b]，f(x)和h(x,η)是有定义的；J(x,D), G(x,D)关于 x 全局 Lipschitz 连续，Lipschitz 系数为

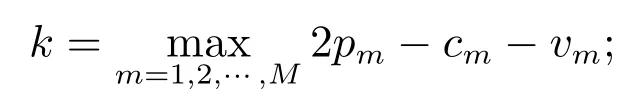
(ii) f(x)和h(x,η)关于x 是全局Lipschitz 连续的，Lipschitz 系数为k；且h(x,η)关于η 也是全局Lipschitz 连续的．

证明 对于结论(i)，由G(x,D)的显式表达式可知，对xm, m=1,2,··· ,M，有

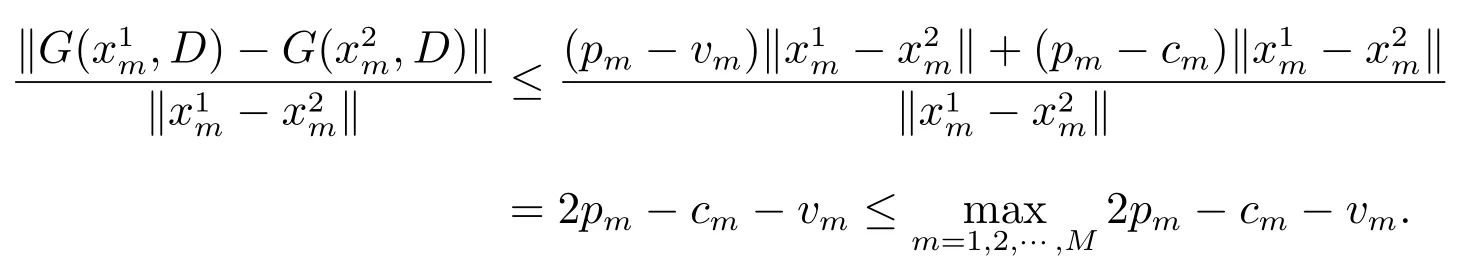
故而J(x,D), G(x,D)关于x 的Lipschitz 系数为

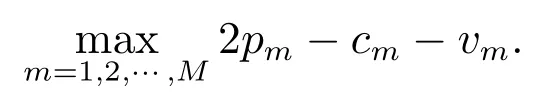
对于结论(ii)，由(i)可知，f(x)和h(x,η)关于x 是全局Lipschitz 连续的，Lipschitz系数为k．又因为H(x,η,D)关于η 是全局Lipschitz 连续的，即

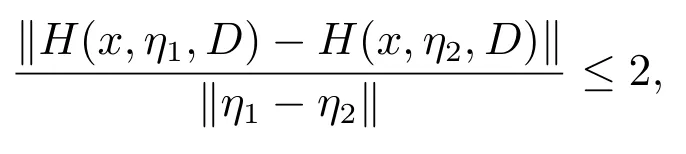
表明h(x,η)关于η 也是全局Lipschitz 连续的．

假设1问题(4)满足一致占优条件(Slater 约束规范)，即存在x0∈X，使得

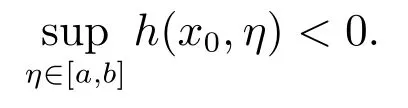
令

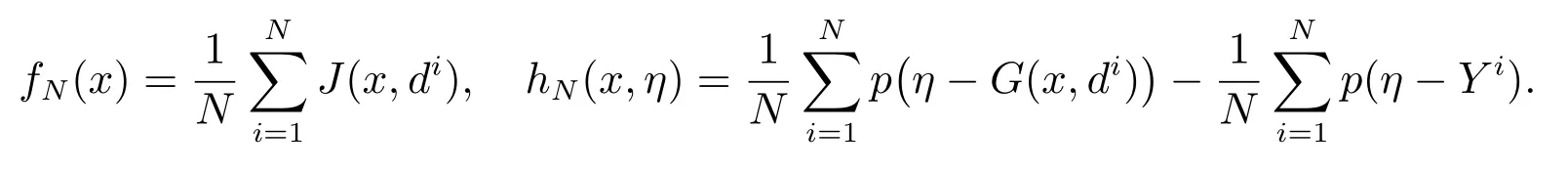
SAA 问题(5)，可以写成如下形式

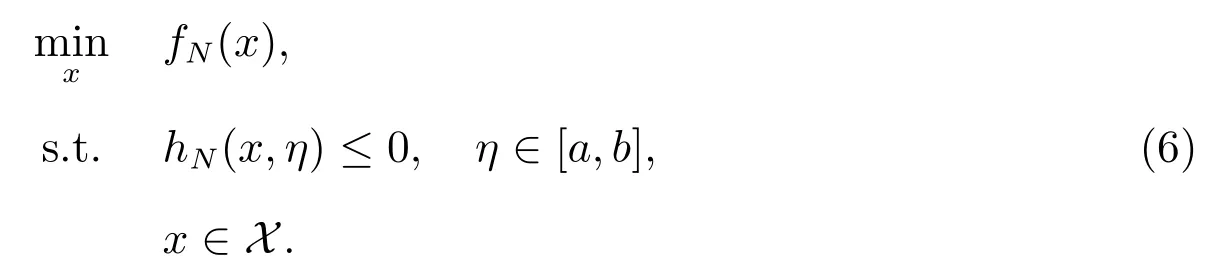
设问题(6)的最优值是zN，接下来证明随样本量N 的增加，zN收敛于真问题(4)的最优值，将样本均值逼近写成特定的概率测度

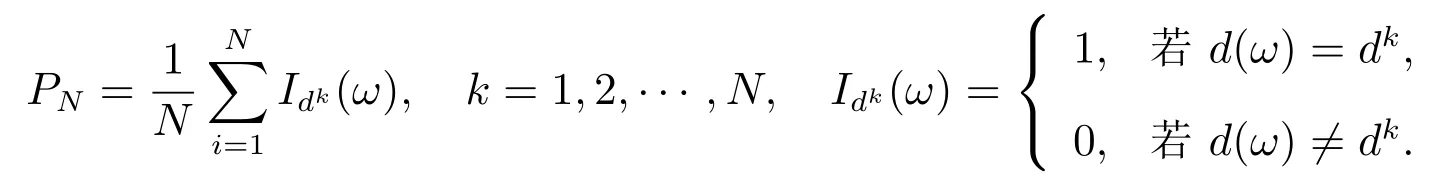
在随机规划中，PN被称为经验概率测度．据此将(6)式改写为

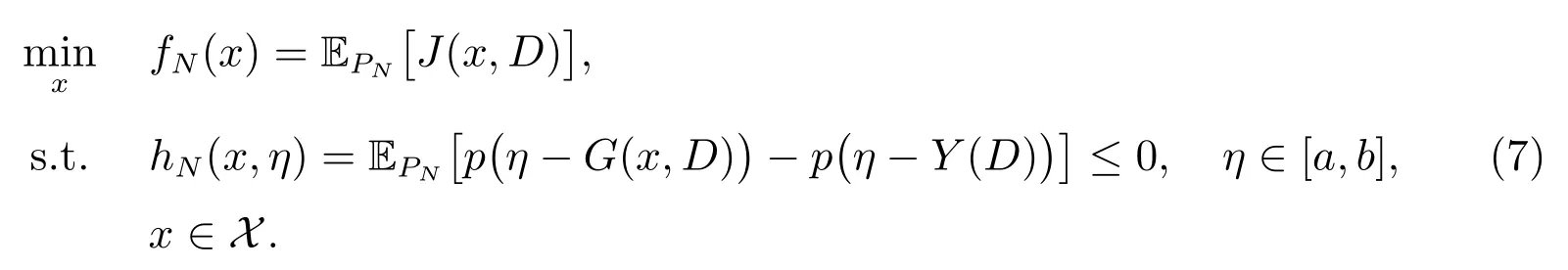
在进行收敛性分析之前定义以下几个符号：设P(Ω)表示所有Borel 概率测度的集合；定义函数集

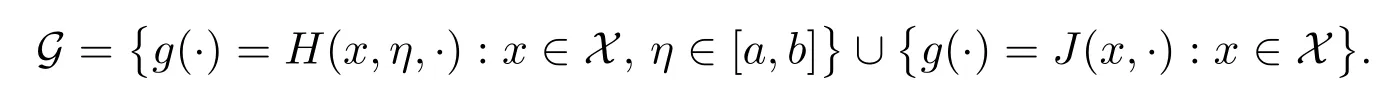
定义PN到P 的伪距离

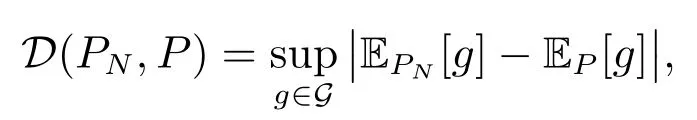
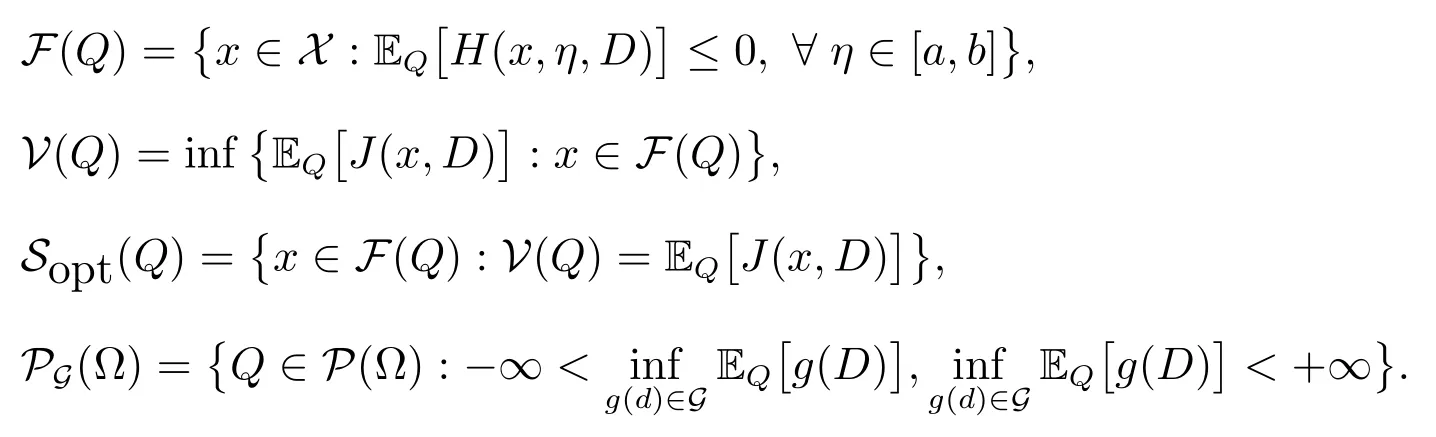
由于H(x,η,·)和J(x,·)是连续的，且X 和[a,b]是紧集，所以PN, P ∈ PG(Ω)且D(PN,P)<∞．

定理1设：

(i) 假设1 成立；

(ii) 命题1 的条件成立及X 是紧集，则：

1) 对于问题(6)的最优值函数V(PN)，当N →∞时，w.p.1 满足

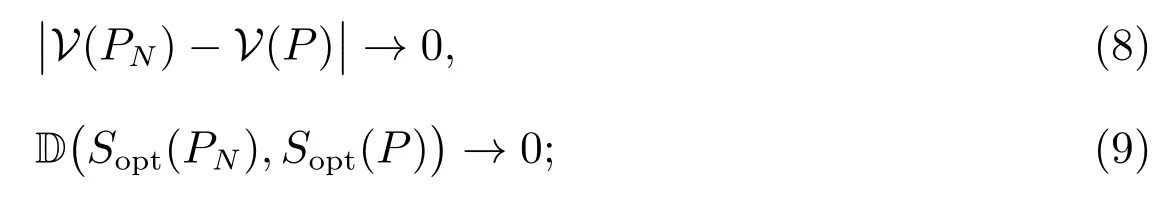
2) 若另有：

(iii) 对任意的x ∈X，当t 趋向于0 时，广义矩函数

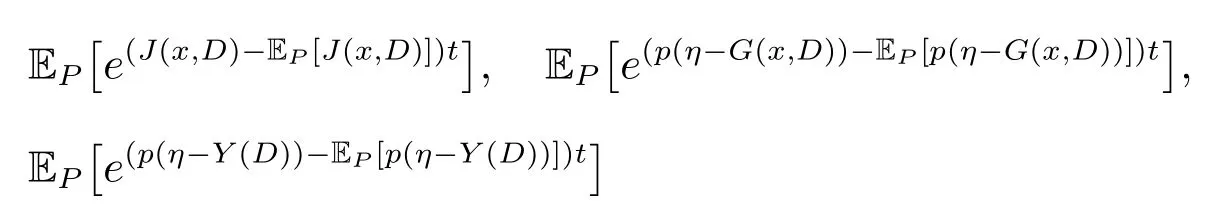
有界，则对任意小的正数γ，存在正整数N∗和独立于N 的正实数C(γ), β(γ)，使得当N ≥N∗时，满足

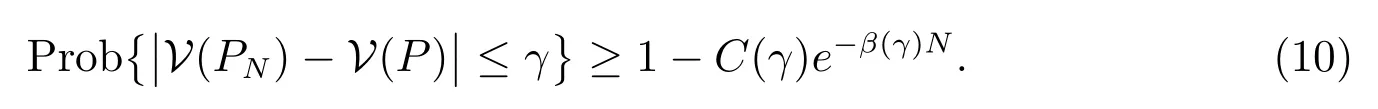
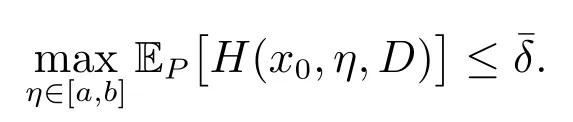
继而由文献[23]定理3.1 的结论(i)和文献[34]定理2.7 的结论(iii)可知，存在正整数L∗>0，使得w.p.1

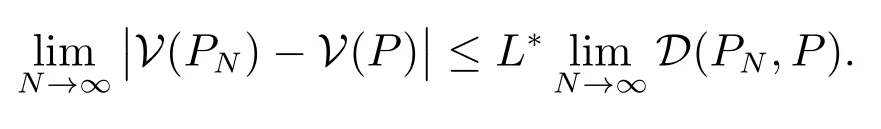
又由命题1 和文献[23]命题3.1 可知，当N →∞时，有D(PN,P)→0，所以有

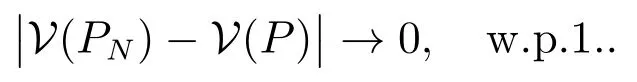
对于(9)式，在命题1 及假设1 的条件下，由文献[34]定理2.7 的结论(ii)可知Sopt(·)在P 处上半连续．结合文献[23]命题3.1 可知

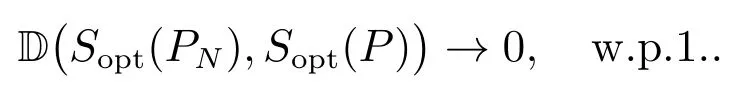
对于(10)式，在条件(iii)下，由命题1 和文献[23]命题3.2 可知，对任意小的正数γ ≤ L∗ϵ∗，存在正整数N∗和独立于N 的正实数C(γ), β(γ)，当N ≥ N∗时

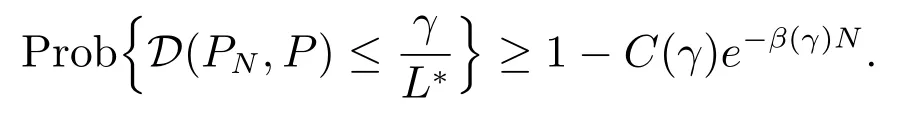
结合文献[34]定理2.7 的结论(iii)，有

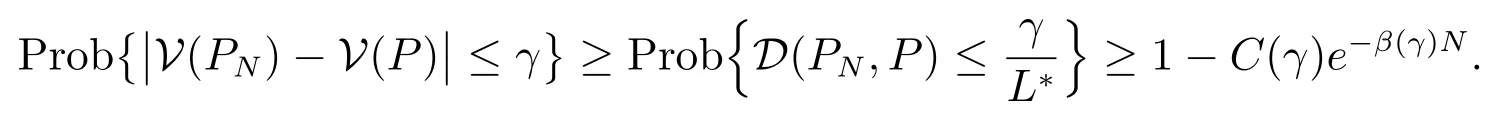
4 数值实验

由于问题(5)是半无限问题，难以求解，所以考虑在特定条件下将其转化为有限问题，即考虑其以下等价形式．

假设2随机变量Y(D)的支持集Y ⊆[a,b]．

在假设2 下，由文献[20]的命题3.2 可知问题(5)等价于

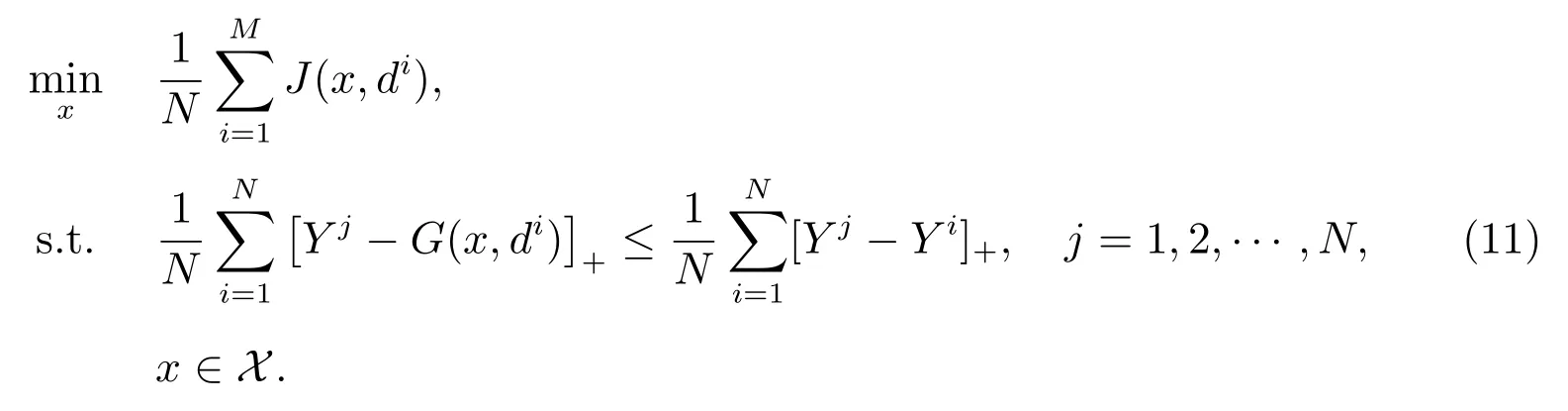
称问题(5)与问题(11)均为SAA 问题．由于问题(5)与(11)的等价性，所以在以下部分以(11)为研究对象．

4.1 切平面算法

Sun 等[26]改进的切平面法适用于解决多个非线性复杂约束的随机优化问题，这里采用该方法求解问题(11)．

算法1

第1 步令迭代次数t=0，误差ϵ=10−5，令S0={x|0 ≤ cTx ≤ α}；

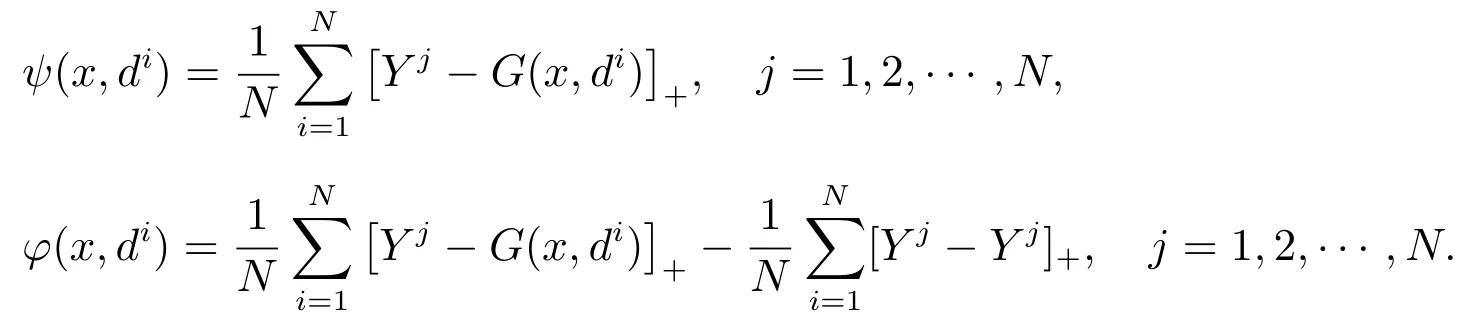
第2 步解决线性规划问题

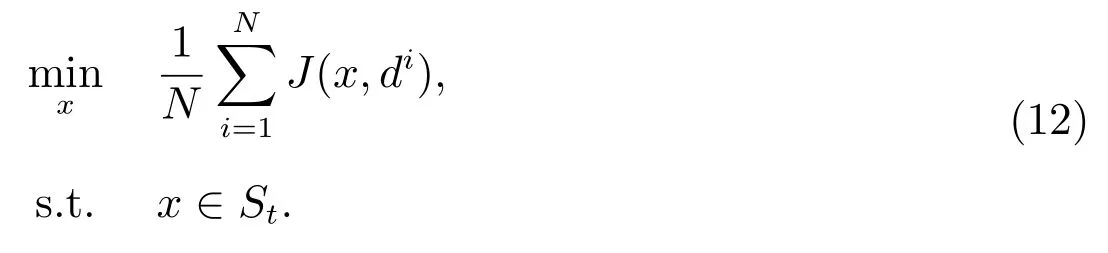
若问题(12)无可行解，则原问题无可行解；否则，设问题(12)的最优解为xt．

第3 步找到，使得

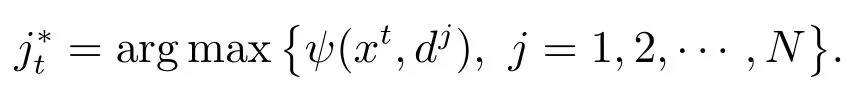
其实质是找到众多约束中违反度最大的约束．构造索引集

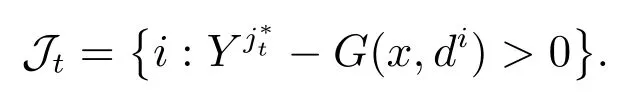
第 4 步若停止，是最优解；否则，构造切平面

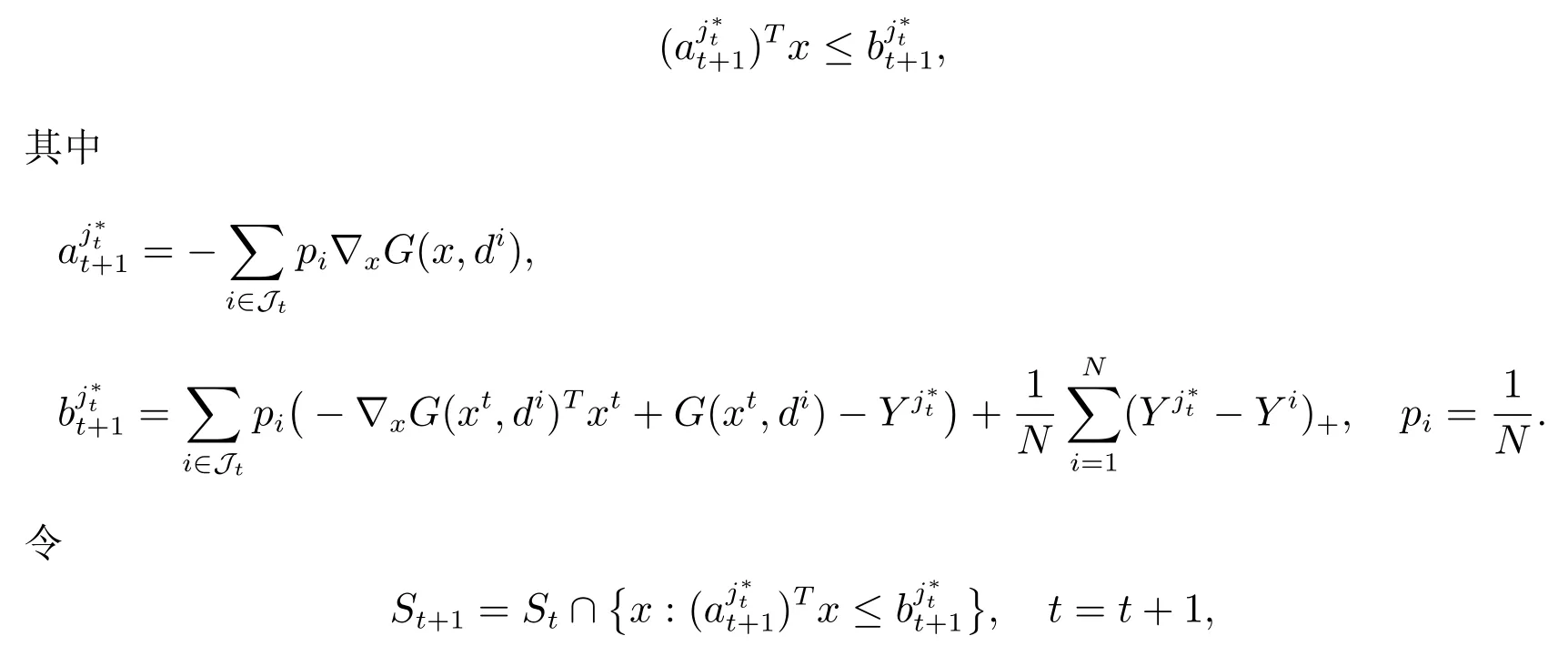
转到第2 步．

4.2 实验及结果分析

本节考虑零售商需要在销售季进行五种产品的交易，即零售商需要在期初确定五种产品的订购量以期获取最大利润．假定五种产品的需求服从不同自由度的χ2分布

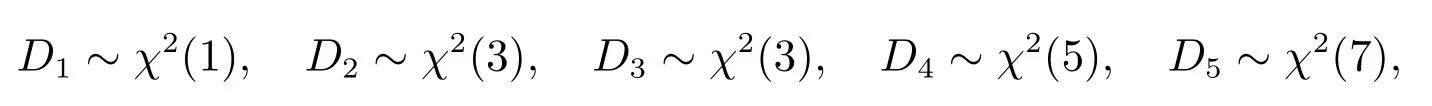
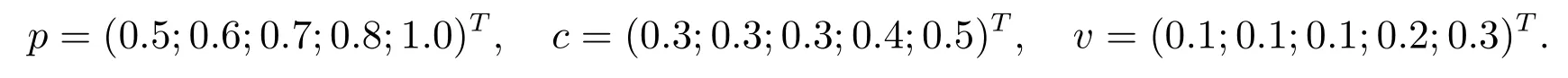
在此基础上设置三个示例，例1 采用模型(1)为参照进行样本内实验，对SSD 模型的收敛性进行验证．例2 在模型(1)为参照下，进行样本外累计预测．例3 以均值-方差(MV)模型为参照模型，进行样本外累计预测．MV 模型即以最小(大)化随机损失(利润)的期望为目标函数，以随机函数的方差来度量风险．对于报童问题带有订购能力约束的MV模型为

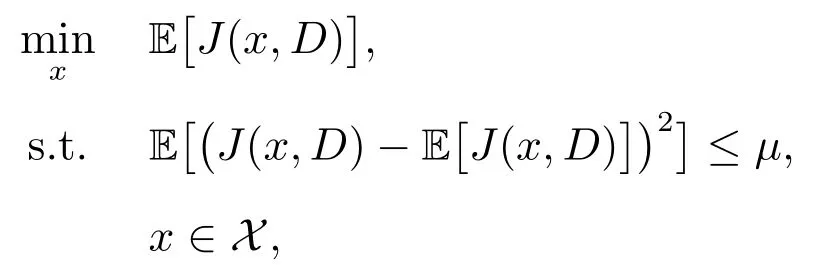
其中µ为常数，该模型也是风险厌恶模型．由于参照模型的最优解也属于紧集X，所以参照随机变量Y(D)的支持集有界，假设2 成立，从而SAA 问题(5)与(11)等价，这里采用算法1 求解问题(11)．

例1SSD 模型收敛性分析数值实验

设资金约束α = 3.5，样本量取10000，求得模型(1)的最优解，作为SSD 模型的参照．然后在SSD 模型的求解中，样本量依次设为100、1000、2000、3500、5500．每个样本量下进行30 次实验，其结果如图1 所示，图中每一个垂直区间表示在对应样本量下30 个最优解的范围．该图显示了SSD 模型下最优解随样本量增大而逐渐收敛的特性．

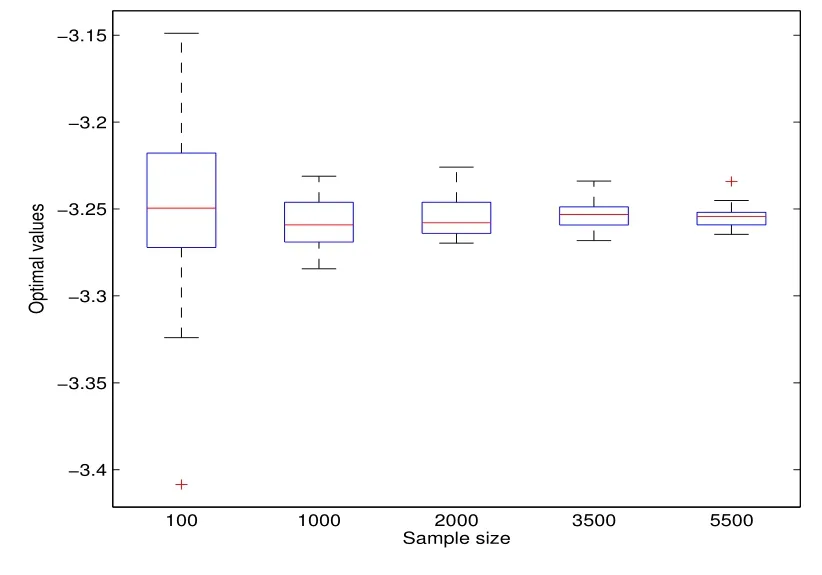
图1: 例1 随样本量增加SAA 问题的收敛性

例2以模型(1)为参照的SSD 模型样本外累计预测

假设零售商在有限购买能力下订购商品并出售，而后将利润累计到资本，直到最优订购量的金额不受资本约束为止．样本量N 取3000，初始资本设为0.7，在此条件下，本例在每轮订购下均进行10 次抽样，求得样本外预测的利润均值，以该均值作为资本累计，经过5 轮累计之后，累计资本大于最优订购量下的成本，停止累计．

本例资本累计的步骤如下：

步骤1在相同初始资本下，模型(1)与SSD 模型各自以其最优订购策略实现其预期利润；

步骤2模型(1)以其自身利润为累计资本，求得最优解；

步骤3模型(1)以SSD 模型利润为累计资本，求得最优利润作为基准；在该基准下，SSD 模型以其自身利润为累计资本，求得最优解；

步骤4返回步骤2．

表1 和图2 均说明，在同样的样本下，平均利润SSD 模型优于模型(1)．图3 显示了第四次样本外累计预测10 次抽样的结果，此时在订购能力约束下，SSD 模型下的利润高于模型(1)，这就使得在SSD 模型下，零售商可实现以更快的速度达到累计资本的目的，以摆脱订购能力约束．图4 显示了第五次样本外累计预测10 次抽样的结果，表明当累计资本充足，即零售商不再受订购能力约束时，SSD 模型能够以更少的投资获得更大的利润．

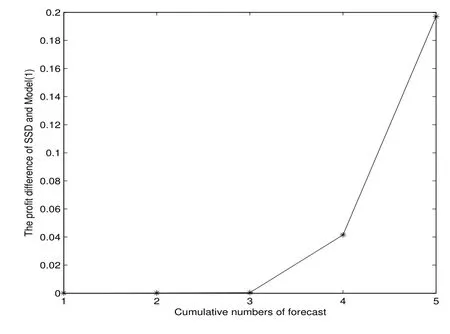
图2: 例2 样本外累计预测平均利润差

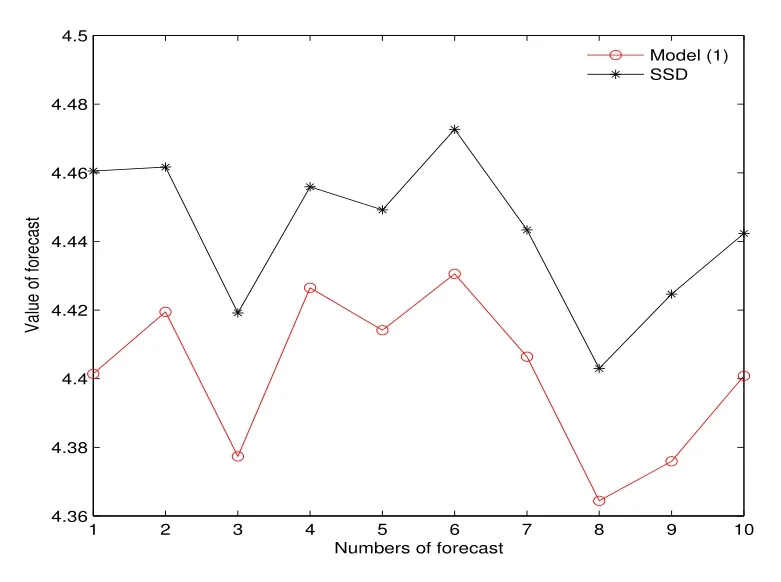
图3: 例2 第四次预测

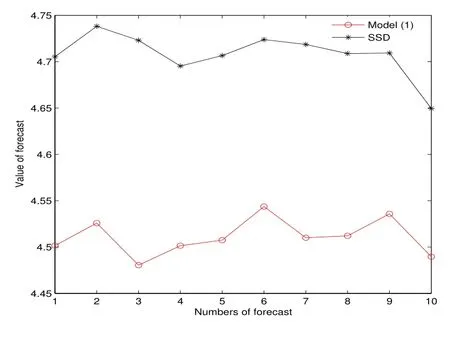
图4: 例2 第五次预测

例3以MV 模型为参照的SSD 模型样本外累计预测

采用例2 的资本累计步骤，以MV 模型为参照，设µ=0.3，所得结果如表2、图5 至图7 所示．

表2、图5 至图7 表明，样本外累计预测下，SSD 模型的利润优于MV 模型，且这种占优趋势随着资本累计越来越明显．其中图6 和图7 分别为第四次、第五次样本外10 次抽样的利润．

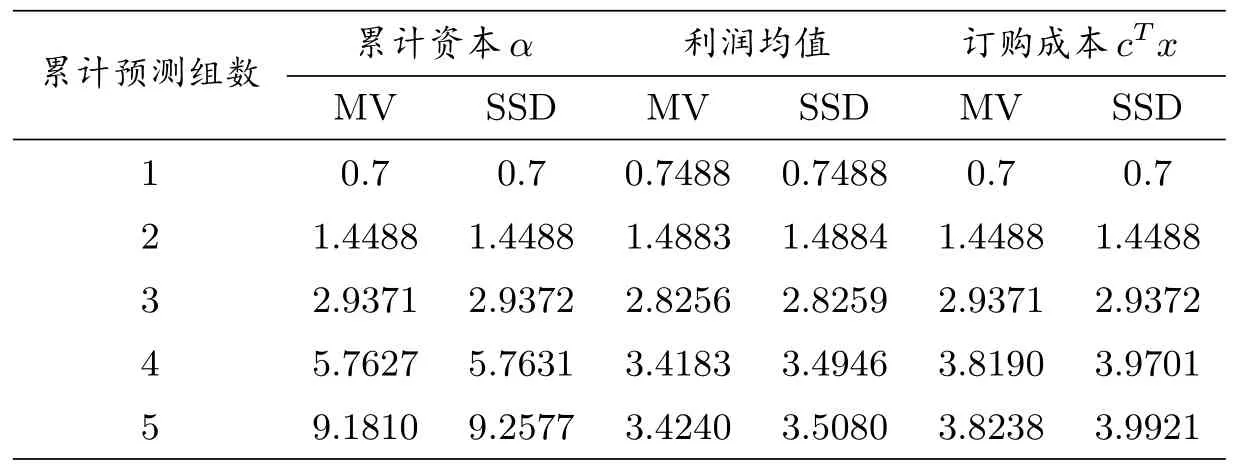
表2: 例3 样本外累计预测

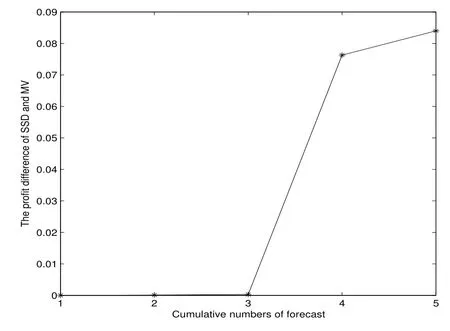
图5: 例3 样本外累计预测平均利润差

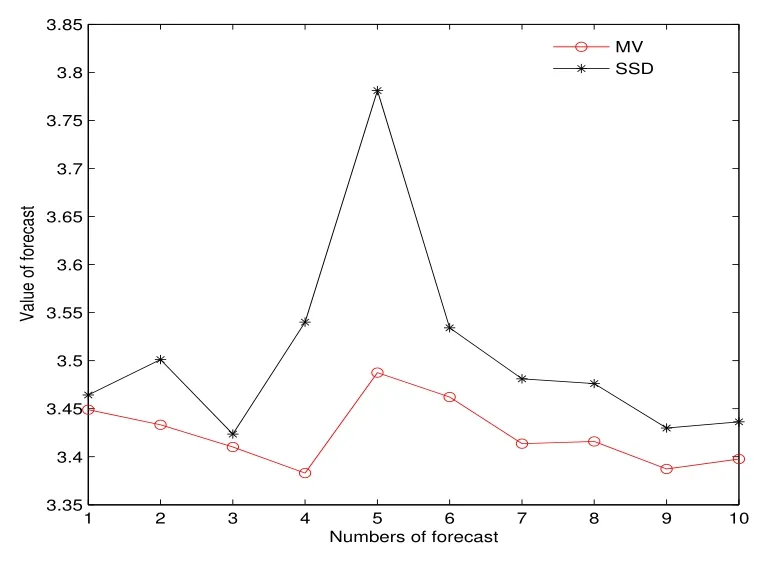
图6: 例3 第四次预测

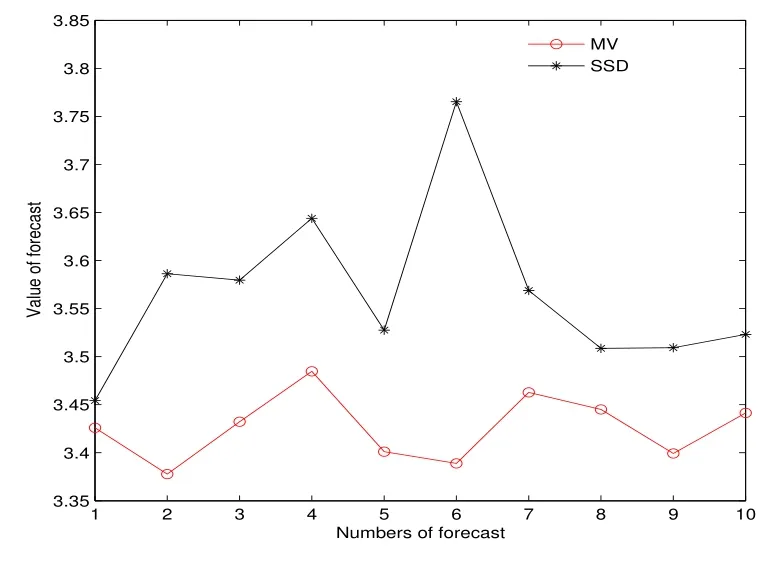
图7: 例3 第五次预测

5 总结

本文以单周期多产品报童问题为背景，在订购能力约束及SSD 约束下进行建模．对SAA 问题进行收敛性分析并通过切平面法对SAA 问题进行求解．以风险中性模型(模型(1))及风险厌恶模型(MV 模型)为参照下，通过样本外预测表明了SSD 模型的优越性．SSD 模型具有良好的风险规避性，决策者可以该模型的订购策略作为自身决策的评价和基准，具有重要的现实意义．基于本文的研究可以继续探讨多产品多周期的情形，以及风险厌恶条件下多级供应链的协调等．