交换半环上半线性空间的线性变换

张兴均， 吴 莉， 王学平*

（1.四川师范大学 数学科学学院，四川 成都610066； 2.阿坝师范学院 数学与计算机科学学院，四川 汶川623002）

2007 年，Di Nola等［1］运用半环、半模等概念在MV-代数中引进了半线性空间的概念，得到了类似于经典线性代数中的相关结论.但也有许多与经典线性代数不同的地方，如：半线性空间的基的向量个数不再唯一、线性无关的向量组不一定能扩张为半线性空间的基等［1］.之后，许多学者开始对半线性空间的基、维数以及同构等进行了大量且细致的研究，如：2010 年，Zhao 等［2］给出了定义在交换的zerosumfree半环上L-半线性空间Vn的基的基数唯一的一个充分条件；2011 年，Shu 等［3］证明了定义在交换的zerosumfree 半环上L -半线性空间Vn的基的基数是相等的充要条件是Vn的每个向量能被基唯一表出，该充要条件还被文献［4］进行了相应推广，并得到了与自由基相关的一些结论.线性变换是研究半线性空间中向量之间关系的有力工具，本文主要介绍了半线性空间上线性变换、幂等变换、可逆变换的概念，定义了线性变换的运算，讨论了幂等变换、可逆变换的一些基本性质，并得到了线性变换的值域与核的一些重要关系.

1 预备知识

下面将给出一些已知的基本定义.

定义1.1［5-6］半环L=（L；+，·，0，1）是满足以下性质的代数结构：

1）（L；+，0）是交换幺半群；

2）（L；·，1）是幺半群；

3）∀r，s，t∈L，r·（s +t）=r·s +r·t 与（s +t）·r=s·r+t·r成立；

4）∀r∈L，0·r=r·0 =0 成立；

特别地，若∀a，b∈L，都有a·b=b·a，则称半环L为交换的.

定义1.2［5］设L=〈L，+，·，0，1〉为半环，A=〈A，+A，0A〉为交换幺半群.如果外积*：L ×A→A满足：∀r，r′∈L，a，a′∈A，

1）（r·r′）*a=r*（r′*a），

2）r*（a+Aa′）=r*a+Ar*a′，

3）（r+r′）*a=r*a+Ar′*a，

4）1*a=a，

称半环L上的半模为L -半线性空间［1］.这里的半模或是左L-半模，或是右L -半模［6］.通常情况下，将半环中的元称为标量或者系数，将半线性空间中的元称为向量.

不失一般性，设以下讨论的半模均为左L-半模.在不混淆的情况下，将（r·r′）*a 写作（rr′）a.设n=｛1，2，…，n｝，则由定义1.2 可给出下面L -半线性空间的例子.

例1.1设L=〈L，+，·，0，1〉是半环.对n≥1，令

其中（a1，a2，…，an）T表示（a1，a2，…，an）的转置.对任意的x =（x1，x2，…，xn）T，y =（y1，y2，…，yn）T∈Vn（L）和r∈L，定义

定义1.3［7］设W是L-半线性空间V的子集，若对任意的x，y∈W，k∈L，有kx∈W，x +y∈W，则称W为L-半线性空间V的子空间.

接下来引入线性相关、线性无关以及基的概念.

定义1.4［1］设〈L，+，·，0，1；*；A，+A，0A〉为L-半线性空间.称表达式

为A中向量组a1，…，an的线性组合，其中，λ1，λ2，…，λn∈L.若向量x能表示为向量组a1，…，an的线性组合，则称向量x能被向量组a1，…，an线性表出（或线性表示）.

定义1.5［1］在L-半线性空间中，单个向量a是线性无关的.若向量组a1，…，an（n≥2）中的任意向量都不能被其余向量线性表出，则称该向量组是线性无关的，否则，称向量组a1，…，an是线性相关的.如果有无限个向量的向量组中任意有限个向量都是线性无关的，则称该向量组是线性无关的.

设M是L-半线性空间V 的非空子集，如果L-半线性空间V 中任意向量都能由集合M 中向量线性表出，则称M 是L -半线性空间V 的生成集［8］.进一步，如果M 还是有限集，则称L -半线性空间V是有限生成的［3］.如果L-半线性空间V的元至多能被非空子集M中元以一种方式表出，则称M 是自由的［4］.显然，自由集一定是线性无关的.

定义1.6［4，6］称L-半线性空间V中线性无关的生成集为V 的基.特别地，称L -半线性空间V的自由生成集为自由基.若V存在自由基，则称V为自由的L-半线性空间.

易见，Vn是自由的L-半线性空间.

2 线性变换

半线性空间V到自身的映射称为V的变换.

定义2.1交换半环上L -半线性空间V 的变换A称为线性变换，如果∀a，b∈V以及∀r∈L，都有：

1）A（a+b）=A（a）+A（b），

2）A（ra）=rA（a）.

注意，在文献［9］中，称满足定义2.1 条件的变换为半线性变换.

例2.1设L =〈L，+，·，0，1〉是交换半环，对任意的a∈V，k∈L，定义K，则K 是线性变换.

明显地，若半环L不是交换的，则上述例子中K不一定是线性变换.特别地，若k 为乘法单位元1，则V的变换K为，这是一个恒等变换，常用E来表示，恒等变换也叫做单位变换.若k 为加法单位元0，则V的变换K 为，这是一个零变换，常用O表示，对∀a∈V，有O（a）=0.

不难从定义推出半线性空间中线性变换有如下简单性质：

1）设A是L-半线性空间V的线性变换，则A（0）=0；

2）线性变换保持线性组合与线性关系式不变；

3）线性变换把线性相关的向量组变为线性相关的向量组.

需要注意的是3）的逆不一定成立，即半线性空间中线性变换可能将线性无关的向量组变为线性相关的向量组.

引理2.1［9］设a1，…，an是交换半环上L-半线性空间V的一组基，b1，…，bn为V中任意n个向量，则存在唯一的线性变换A使得对任意i∈n，A（ai）=bi.

定义2.2设A、B为交换半环上L-半线性空间V 中的2 个线性变换，定义它们的乘积AB：∀a∈V，（AB）（a）=A（B（a）），则AB 依然是线性变换.

与经典线性代数一样，在半线性空间中线性变换的乘法满足结合律，但一般情况下，不满足交换律，也不满足消去律.

定义2.3设A、B为交换半环上L-半线性空间V 中的2 个线性变换，定义它们的加法A +B：∀a∈V，（A+B）（a）=A（a）+B（a），则A+B依然是线性变换.

容易验证，半线性空间中线性变换的加法满足交换律与结合律，线性变换的乘法对加法满足左右分配律.

定义2.4设A为交换半环上L -半线性空间V的线性变换，若在L-半线性空间V上存在线性变换B使得AB =BA =E，则称变换A 为可逆的，变换B称为A的逆变换，记作A-1.

容易验证A-1也是线性变换，并且变换A 的逆是唯一的.

命题2.1在L-半线性空间V中，可逆线性变换把线性无关的向量组变为线性无关的向量组.

证明在L-半线性空间V中，设向量组a1，a2，…，an线性无关.若A 为V 中的可逆变换，接下来证明向量组A（a1），A（a2），…，A（an）也是线性无关的.

首先，不妨设向量组A（a1），A（a2），…，A（an）线性相关，且

A（a1）= k2A（a2）+… + knA（an），

其中k2，…，kn∈L，则根据线性变换定义有

定理2.1设A 为交换半环上有限生成的L-半线性空间V的线性变换，若A 是可逆的，则a1，…，an是基当且仅当A（a1），…，A（an）也是V的基.

证明必要性 由A 是可逆变换可知，对任意的y∈V，都存在向量x∈V 使得A（x）=y.不妨设a1，…，an是V的一组基，且，其中ki∈L，i∈n，则A（x）=y=k1A（a1）+…+knA（an）.

也就是说，V 中任一向量都能被向量组A（a1），…，A（an）线性表出，并且由命题2.1 知，A（a1），…，A（an）线性无关，因此，A（a1），…，A（an）是V的一组基.

充分性 ∀x∈V，有A（x）∈V，若A（a1），…，A（an）是V的一组基，则A（x）能表示成向量A（a1），…，A（an）的线性组合.不妨设A（x）= k1A（a1）+… + knA（an），其中

根据线性变换定义，有

又因为A是可逆的，用A-1作用于上式两端，则

也就是说，任意向量x都能表示为向量组a1，…，an的线性组合，又由命题2.1 知，向量组a1，…，an是线性无关的，因此a1，…，an是V的一组基.

由例2.2 易见，定理2.1 中，A 是可逆的条件一般不可去.

推论2.1A 为交换半环上有限生成的L -半线性空间V的线性变换，若A 是可逆的，则a1，…，an是V的自由基当且仅当A（a1），…，A（an）也是V的自由基.

设A为交换半环上L-半线性空间V的线性变换，n为非负整数，定义，称为A的n次幂.特别地，定义A0=E.若A2=A，则称A为幂等线性变换.

命题2.2设A为交换半环上L -半线性空间V的可逆幂等线性变换，则A是单位变换.

证明因为A为可逆线性变换，则有AA-1=E.又A为幂等线性变换，即A2=A，则

所以A=E.

3 线性变换的值域与核

设A为L-半线性空间V的线性变换，记Im（A）=｛A（a）：a∈V｝，称Im（A）为A的值域.记Ker（A）=｛a∈V：A（a）=0｝，称Ker（A）为A的核.

不难证明，Im（A）与Ker（A）都是L-半线性空间V的子空间.

定义3.1设A为L-半线性空间V的线性变换，W是V的子空间，若∀a∈W 有A（a）∈W，则称W是A的不变子空间.

命题3.1设A与B是L-半线性空间V的2 个线性变换，若BA = AB，则Im（A）与Ker（A）都是B的不变子空间.

证明1）∀a∈Im（A），存在b∈A 使得a =A（b），于是B（a）=B（A（b））=（BA）（b）=（AB）（b）=A（B（b）），而B（b）∈V，则A（B（b））∈Im（A），即B（a）∈Im（A）.由不变子空间定义，Im（A）是B的不变子空间.

2）∀a∈Ker（A），有A（a）=0.又BA =AB，则A（B（a））=（AB）（a）=B（A（a））=B（0）=0，即A（B（a））=0，于是B（a）∈Ker（A）.

由不变子空间定义，Ker（A）是B的不变子空间.

定理3.1设A 与B是L -半线性空间V 的2个线性变换，则A 与B 都是幂等的且Im（A）=Im（B）的充分必要条件是AB=B且BA=A.

证明必要性 设A 与B 都是幂等线性变换且Im（A）= Im（B），则∀a ∈V，有B（a）∈Im（B）=Im（A）.存在一向量b∈V，使得B（a）=A（b），（AB）（a）=A（B（a））=A（A（b））=A2（b）=A（b）=B（a），即AB =B.同理可得BA=A.

充分性 ∀a∈V，有A（a）∈Im（A）⊆V.由AB=B以及BA=A，可知A（a）=（BA）（a）= B（A（a））∈Im（B），从而Im（A）⊆Im（B）.同理可得Im（B）⊆Im（A），故

即线性变换A是幂等的.同理可得线性变换B 也是幂等的.

命题3.2设A 与B 是L -半线性空间V的2个线性变换，若AB=A且BA=B，则Ker（A）=Ker（B）.

证明∀b∈Ker（A），由BA =B知，B（b）=（BA）（b）= B（A（b））= B（0）=0，所以b ∈Ker（B），从而有Ker（A）⊆Ker（B）.同理可得Ker（B）⊆Ker（A），即Ker（A）=Ker（B）.

注3.1一般说来，命题3.2 的逆命题不成立.

例3.1设L=〈L，+，·，0，1〉为半环，其中L为图1 所示的格，+ =∨，·=∧.在L-半线性空间V2中定义A；B，其中，a∈V2，

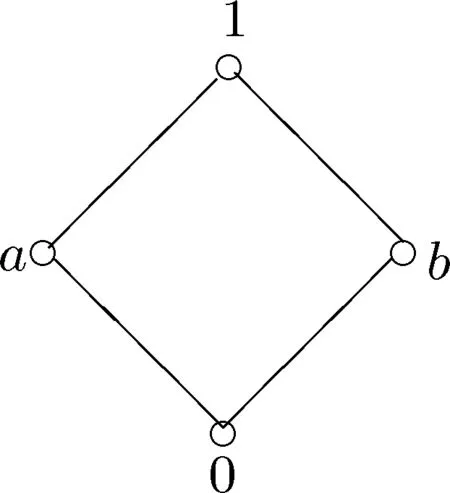
图1 分配格Fig.1 Distributive lattice

定理3.2设A与B是有限生成的L-半线性空间V的2 个线性变换，则Im（B）⊆Im（A）的充分必要条件是存在线性变换C使得B=AC.

证明必要性 若Im（B）⊆Im（A）.设a1，…，an是V 的一组基，则存在V 中的一个向量组b1，…，bn使得B（a1，…，an）=（Ba1，…，Ban）=（Ab1，…，Abn）=A（b1，…，bn）.又由引理2.1知，存在V 中的线性变换C 使得C（a1，…，an）=（b1，…，bn），所以B（a1，…，an）=A（b1，…，bn）=AC（a1，…，an）.由于a1，…，an是L -半线性空间V的基，故B=AC.

充分性 假设V中存在线性变换C 使得B =AC，则∀a∈V，有B（a）=AC（a）=A（C（a））.由于C（a）∈V，因此，A（C（a））∈A（V），即B（a）∈A（V），所以Im（B）⊆Im（A）.

注3.2定理3.2 中线性变换C一般不唯一.

例3.2考虑模8 的剩余类环上的线性空间V2，作V2上的线性变换A、B、C1、C2如下显然

命题3.3设A与B是L-半线性空间V的2个线性变换，若在V中存在线性变换C使得CA=B，则Ker（A）⊆Ker（B）.

证明若在L-半线性空间V中存在线性变换C使得CA =B，则∀a∈Ker（A），有A（a）=0，（CA）（a）=C（A（a））=C（0）=0，即B（a）=0，所以a∈Ker（B），即Ker（A）⊆Ker（B）.

注3.3一般说来，命题3.3 的逆命题不成立.

例3.3设L为例3.1中半环，在L-半线性空间V2中定义A；B：，其中，a∈V2，

由定理3.2 与命题3.3 可得下面推论成立.

推论3.1设A与B是有限生成的L-半线性空间V的2 个线性变换，则Im（AB）⊆Im（A），Ker（B）⊆Ker（AB）.

定理3.3设A与B是L-半线性空间V的2 个线性变换，Im（B）⊆Ker（A）的充分必要条件是AB=O.特别地，Im（A）⊆Ker（A）的充分必要条件是A2=O.

证明必要性 因为有Im（B）⊆Ker（A），∀a∈V，则B（a）∈Im（B）⊆Ker（A），即A（B（a））=（AB）（a）=0.

由a的任意性知AB=O.

充分性 设AB=O，在Im（B）中任取一向量B（a），a∈V，则A（B（a））=（AB）（a）=O（a）=0.

因此B（a）∈Ker（A），即Im（B）⊆Ker（A）.

特别地，令B=A，则有

由定理3.3 易见下面推论成立.

推论3.2设A与B是L-半线性空间V的2 个线性变换，则B（Ker（AB））⊆Ker（A）.特别地，A（Ker（A2））⊆Ker（A）.

推论3.3设A与B是L-半线性空间V的2 个线性变换，若A2=O 且Im（B）=Im（A），则AB=O且Im（B）⊆Ker（A）.

证明若A2=O，则由定理3.3 知，Im（A）⊆Ker（A），又Im（B）=Im（A），所以有Im（B）=Im（A）⊆Ker（A）.

再根据定理3.3 得AB=O.

根据定理3.3 及推论3.3 得下面推论成立.

推论3.4设A 与B是L -半线性空间V 的2个线性变换，若A2=B2=O 且Im（B）=Im（A），则AB=BA=O且

设V1、V2是L-半线性空间V的子空间，所谓V1与V2的和，是指由所有能表示为（其中x1∈V1，x2∈V2）的向量组成的子集合，记作

推论3.5设A与B是L-半线性空间V的2 个线性变换，则A2=B2=O 与AB =BA =O同时成立的充分必要条件是

证明因为A2=B2=O，AB =BA =O，则根据定理3.3 知

因此

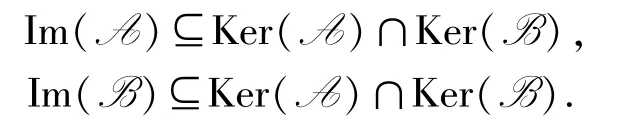
从而

反之，设

则

由定理3.3 得

定理3.4设A与B是L-半线性空间V的2个线性变换，则Ker（A）⊆Im（B）的充分必要条件是Ker（A）=B（Ker（AB））.特别地，Ker（A）⊆Im（A）的充分必要条件是

证明必要性 设Ker（A）⊆Im（B），∀a∈Ker（A），有A（a）=0.由于a∈Ker（A）⊆Im（B），所以a∈Im（B），则存在向量b∈V，使a=B（b）.因此（AB）（b）= A（B（b））= A（a）=0，所以b ∈Ker（AB）.从而有a=B（b）∈B（Ker（AB）），又a∈Ker（A），所以Ker（A）⊆B（Ker（AB））.

另一方面，若∀c∈B（Ker（AB）），则存在向量d∈Ker（AB）使得B（d）=c，（AB）（d）=0.因此A（c）= A（B（d））=（AB）（d）=0，即c∈Ker（A），所以B（Ker（AB））⊆Ker（A），即

充分性 设Ker（A）=B（Ker（AB）），显然Ker（A）= B（Ker（AB））⊆Im（B）.特别地，令B=A，显然

定理3.5设A为有限生成的L -半线性空间V的线性变换，若A 是单变换，则Im（A）的基的原像构成V的基.

证明由题设易知Im（A）= V，因此结论成立.

注3.4一般说来，定理3.5 中单变换条件不可去.