环向张拉弹性肋可展结构概念与初步分析

张 福，张天昊，吴明儿∗，王晓凯，陈晓峰，周 鑫

1 引言

空间可展结构因具有收纳与展开2种不同使用状态，在航天领域得到广泛应用[1]。其中，空间可展天线结构在军事侦察、高分辨率对地观测、移动卫星通信等任务中发挥着重要作用。随着航天工程相关领域应用的发展，对大口径、高精度空间可展天线的需求越发迫切[2-3]。

在实际应用中，现有可展结构体系难以同时满足口径与精度的要求。固面可展天线结构虽然具有较高的精度，但由于收纳比的限制，难以应用于大口径可展天线任务[4-5]；充气式可展天线结构虽然可提供高收纳比与大口径，但反射面精度较差[6-7]。在现有可展天线结构体系中，索网可展天线结构兼顾口径与精度的需求，理论上可应用于10 m级口径的高精度工程任务。但存在以下问题难以付诸实践：①随着天线口径的增大，为实现较高精度要求，反射面索网的拉索数量势必亦随之增加，而实际工程中，可展天线的索网型面精度取决于对每一根索段的长度与张力的调节及控制，拉索数目的增加使实际结构型面精度的调节变得尤为繁琐，反之制约反射面型面精度；②由于拉索本身几乎没有结构刚度，需要对拉索施加一定预张力以提高天线结构基频，也增加了反射面高精度控制的难度。现有成功应用案例主要局限于S波段及L波段[8-10]，型面精度调整的辅助方法在实际工程中的应用较少，主要仍采用人工尝试性调整方法[11]。因此，可展大口径天线结构的高精度问题亟待得到解决，新型可展结构的研究具有重要的理论意义与实际应用价值。

本文设计出一种环向张拉的弹性肋可展结构，在增加可展天线结构口径的同时，实现反射面型面精度的提高，并分析受力机理，通过数值优化方法分析可展天线结构可能达到的型面精度。

2 结构体系

2.1 结构概念

环向张拉弹性肋可展结构采用含有一定抗弯刚度的弹性肋与受张拉的柔性索为天线反射面支撑材料，通过可展桁架实现结构的展开与收纳(图 1)。

展开状态下，可展天线结构中的弹性肋受到拉索的张拉，通过优化设计可近似变形为反射抛物面上的曲线。图1所示的弹性肋与环向索将反射面分割为若干小型曲面四边形网格，每个网格拥有拉索定义的直线边界与弹性肋定义的曲线边界(图2(a))。与仅由直线边界(图2(b))定义的传统索网可展天线结构相比，曲线边界减少网格的划分数量，更加适用于大口径可展天线的工程实践[12-13]。此外，弹性肋自身具有一定结构抗弯刚度，与传统索网可展天线结构相比，可提高结构整体基频。辐射状六边形可展桁架具有良好拓扑性能，可将此结构用于模块化可展结构体系，进一步增大高精度空间天线的口径。

图1 环向张拉弹性肋可展结构概念模型Fig.1 Deployable structure with circularly tensioned elastic ribs

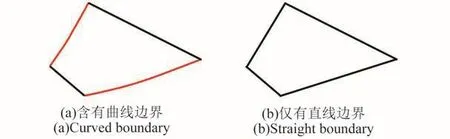
图2 曲线边界与直线边界Fig.2 Curved&straight boundaries

日本宇宙航空研究开发机构(Japan Aerospace Exploration Agency，JAXA)在 VSOP-2项目中曾提出弹性肋可展天线结构方案[14-15]。本文提出的结构具有更高对称性，其张力阵的设计及弹性肋与可展桁架之间的受力机理有别于以往结构，大大简化了结构的找型与优化过程。

2.2 结构构成

环向张拉弹性肋可展结构包括：反射面支撑结构、反射面以及可展桁架结构等(图3)。支撑结构由环向索、弹性肋以及反向张力阵等组成。

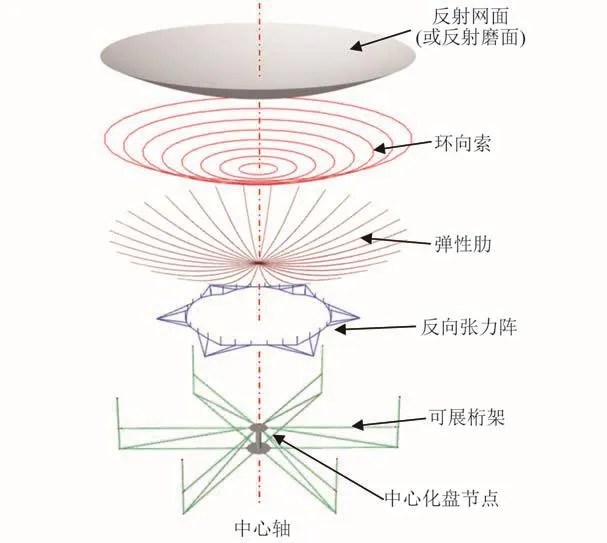
图3 结构主要组成部分Fig.3 Major components of structural system

1)无应力状态下，平直的弹性肋具有一定抗弯刚度，呈辐射状倾斜布置，与中心花盘节点铰接，具有1个转动自由度；相邻弹性肋之间由若干柔性索段相连，由于弹性肋具有高度对称性，索段首尾相连，近似呈环状；反向张力阵将弹性肋与可展桁架相连接，在反向张力阵与环向拉索的张力作用下，弹性肋发生弯曲变形，共同组成天线反射面的支撑系统。

2)天线反射面可采用金属网反射面或薄膜反射面，铺设于由环向索与弹性肋定义的曲线四边形网格。

3)6组平面可展桁架单元轴对称辐射布置，共用中心花盘节点，用于支撑上部天线结构。

2.3 展开与收纳方式

收纳状态下，结构呈直筒状，弹性肋自然伸直，可展桁架收拢，包围在弹性肋外围(图4)。环向索与反向张力阵拉索松弛，反射面亦无张力，折叠于弹性肋周围。

可展桁架通过电机或弹性元件等驱动方式展开。随着可展桁架的展开(图5)，反向张力阵逐渐张紧，带动弹性肋绕中心花盘节点旋转；由于环向索的约束作用，弹性肋开始发生弯曲变形；最终，柔性拉索张拉至预定数值，弹性肋变形至设计形状，反射面张紧，结构呈展开状态。

在展开过程中，可展桁架不仅带动其他构件运动，还在结构完成展开后维持结构稳定。在完全展开状态下，可展桁架运动构件锁定，从而避免拉索及反射面内的预张力发生松弛，维持结构刚度及稳定性。可展桁架基本单元形式众多，技术较为成熟，在 AstroMesh[8]以及 ETS-VIII[16]等项目中均已成功应用。

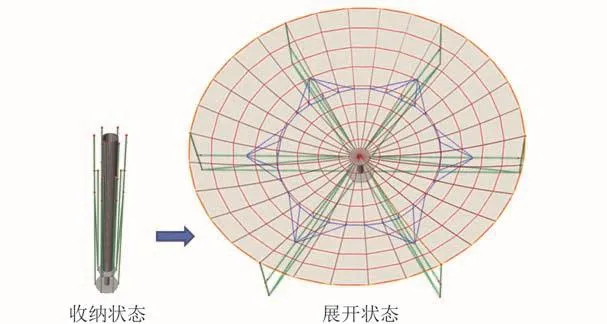
图4 结构展开与收纳Fig.4 Stowed&deployed states

图5 可展桁架的展开Fig.5 Deployment of supporting truss

3 受力机理

环向张拉弹性肋可展结构通过弹性肋的弯曲变形实现反射面边界的成型。弹性肋一端与中心花盘节点铰接，弹性肋同时受到反向张力阵拉索与环向拉索的共同作用。其中，各组环向拉索在弹性肋上产生的作用力的合力为指向中心花盘节点的近似水平力，而反向张力阵则将竖直向下的拉力作用于弹性肋(图6(a))。环向拉索除了使弹性肋发生变形外，还具有箍紧作用，可提高结构的固有频率。

传统的索网可展天线结构由张力阵将前后索网相连接，为了使前索网的形状尽可能接近目标曲面，索网分段数目增加，张力阵的调节较为复杂(图6(b))。采用弹性肋的方法通过调节较少的反向张力拉索来生成高精度反射面网格。

由于弹性肋在环索与反向张力阵的共同拉力作用下达到平衡状态，弹性肋的自由端无需额外约束或支撑。以可展结构的1/6模型(图7(a))为例。可展桁架外端的立柱虽然与弯曲变形的弹性肋自由端接触，但并无支座反力，仅用于增加结构整体性和固有频率，改善动力性能。

可展天线反射面支撑结构部分具有高度的对称性，每一根弹性肋具有相同的受力机理(图7(b))。可以对反向张力阵进行找型设计，使得每一根弹性肋在相同位置产生竖直向下的拉力。

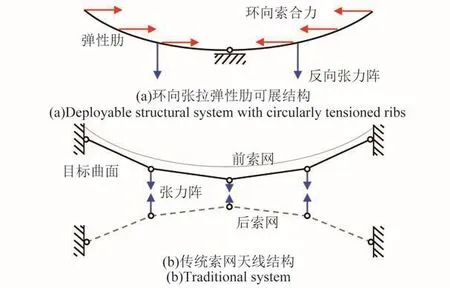
图6 结构受力示意图Fig.6 Tension in structural system

图7 结构单元Fig.7 Structural elements

4 型面精度优化分析

环向张拉弹性肋可展结构的反射面型面通过在反向张力阵下发生弯曲变形的弹性肋保证。为了考查型面精度，通过数值模型进行计算，优化弹性肋形状与受力，并对引起型面精度变化的不同影响因素进行对比与讨论。

4.1 数值模型

根据可展天线结构反射面支撑部分的对称性，其受力机理可离散简化为单根弹性肋在索力作用下的弯曲变形。本文采用有限单元法对单根弹性肋的弯曲变形进行数值计算，模拟其曲面成型过程。

有限元数值模型见图8，算例中弹性肋部分采用梁单元，将弹性肋分为n段，在无应力状态下的初始长度矩阵，其中，lR1、lR2、…、lRn为每段梁单元的长度。假设弹性肋为矩形截面，将每段截面高度 h1、h2、…、hn写成矩阵形式，弹性肋最左端节点与中心花盘固定铰接，为了模拟环向索力产生的合力，其余节点施加水平力其中fH1、fH2、…、fHn为每个节点力大小。分段数n可以根据弹性肋的形状、精度要求决定，本算例中取n=8，将弹性肋分为8段，每段再根据长度等分为5个梁单元，总共40个梁单元。

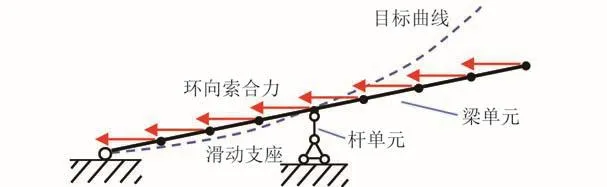
图8 数值模型Fig.8 Numerical model

梁单元中心节点与竖直的杆单元相连接，用以模拟反向张力阵的竖向拉力。杆单元下端定义为滑动支座，使得杆单元始终竖直受拉。杆单元内索力的大小可以通过改变其原始长度lc的方法进行控制。

采用非线性有限元方法对上述数值模型进行计算，可以得到弹性肋在环向索力及反向张力下的变形结果。将其与目标曲线进行对比，便可求得在此条件下的型面误差。

4.2 优化方法

采用遗传算法(Genetic Algorithm，GA)对可展天线结构的型面精度进行优化。由于遗传算法是一种模仿生物遗传学原理的数值优化算法[17]，不依赖于具体问题，且可以寻找依靠人脑直觉难以发现的近似解，适用于对精度影响因素及设计变量关系尚不明确的结构体系。

通过遗传算法寻找能够使得弹性肋型面与设计型面的均方根误差值RMS最小的几何尺寸以及索力分布。将目标优化问题定义为式(1)：

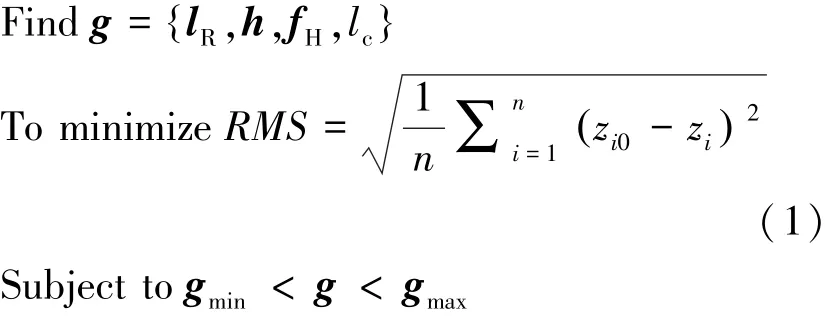
其中，设计变量g包括几何变量lR、h、lc以及环索索力fH；目标函数值为RMS，表征型面误差；n为计算RMS时使用的节点数量；zi与zi0分别为第i节点z坐标及其对应于目标几何上的坐标值。

遗传优化过程中，考虑计算能力与遗传多样性，每一代采用个体数为40，对其进行非线性有限元计算，进行繁殖优化，当 RMS值小于0.01 mm时或遗传代数大于500时停止优化计算。

设计变量众多，为分析不同设计变量给结构型面误差带来的影响，选取不同变量的组合作为设计变量，分别进行数值优化分析。为简化计算，将目标函数值RMS定义为2类：①按弹性肋的梁单元上的节点与目标曲线(抛物线)上对应理想点之距离的均方根计算，记为RMS1；②按肋之间反射面节点与目标曲面(抛物面)上点之距离的均方根计算，记为RMS2。

4.3 结果与讨论

以口径D=4 m，焦径比F/D=0.5的可展天线结构为例，对不同组合的设计变量进行优化分析。首先目标函数值RMS1进行优化。弹性肋采用铝合金材质，截面宽度为5 mm。表1对选取不同设计变量组合进行优化，并将最优解进行对比。其中，“O”代表将此变量作为设计变量优化，而“Ⅹ”代表将其数值人为定义，优化过程中不进行变动。从表1可以看出，索力分布fH的改变对优化效果并不明显，选取变量lR，h以及lc对型面精度的提高最为有效。根据结构基频给定自定索力的条件，寻找到最优解。例如，如果将水平力定义为8个大小为1 N的外力时，对C组变量进行优化，当几何尺寸lR、h为表2设定数值，lc取值为0.975 m时，可以得到最小RMS1为0.227 mm。

表1 各算例组模型的设计变量选取Table 1 Design parameters of each group

表2 最优解设计变量取值Table 2 Optimal design values

h的数值先增大后减小，表明弹性肋为变截面阶梯状构造，梁单元以固定铰支座为起点，截面呈中间厚两端薄的形状。正是其抗弯刚度的局部差异使得弹性肋在发生变形时接近目标曲线。

综上可对支撑反射面的弹性肋进行高精度设计，然而可展天线的使用性能最终归于反射面的型面精度。即使弹性肋与理想抛物面完全重合，仍难以保证张拉于曲线四边形内的反射面的型面精度。因此，有必要将优化问题的目标函数值进一步定义为反射面的均方根误差值，即本文的RMS2值。

基于本结构具有的高度对称性，将反射面简化为2根弹性肋之间的柱状曲面(图9)。相邻梁单元的节点相连接，并将形成的线段近似为位于反射面上的控制点。由此求得的节点与理想抛物面RMS2值，并将RMS2作为目标函数值，对表1的C组变量进行遗传优化求解。需要指出，当反射膜面或反射网面双向张拉铺设形成非负高斯曲率的曲面时，通常会出现反枕现象。由于计算模型反射面狭窄，本文近似采用柱面进行优化计算(单向张拉)，暂不考虑反枕带来的误差增大问题。

图9 反射面RMS2Fig.9 RMS2 of reflector surface

分析4 m口径天线的反射面精度与焦径比及弹性肋数目的关系(图10)。弹性肋数目的增加将反射面分割为更为精细的网格，有助于其型面误差的减小；但是弹性肋数目的增加将不可避免地增加结构质量。焦径比的增大使反射面较为平坦，在相同条件下求得的最优解的RMS2较小。由图10可知，当采用30根弹性肋焦径比为0.5时，4 m口径天线反射面型面误差RMS2小于1.0 mm。对大口径可展天线结构进行模块化设计时，单个模块焦径比会更大，单个模块反射面型面精度可以进一步提高。

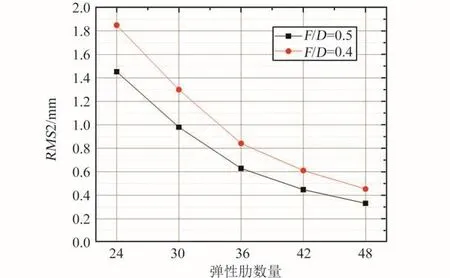
图10 弹性肋数量与型面精度Fig.10 Number of elastic ribs and RMS2

5 结论

1)将弹性肋、柔性拉索以及可展桁架相结合，设计出一种具有高度对称性的可展结构形式，可应用于具有较高反射面型面精度要求的可展天线结构。结构通过环向索与反向张力索使变截面弹性肋发生弹性弯曲变形，从而实现对反射面型面精度的控制，结构的展开与收纳依靠可展桁架的变形完成。基于结构的对称性，将结构整体受力机理简化为单根大变形梁的受力，便于型面精度的优化设计。

2)通过遗传算法，对可展天线结构可能达到的型面精度进行了考查。结果表明：采用变截面梁对反射面型面误差的减小较为有效；反射面型面精度与天线焦径比、弹性肋数目有关，含有30根肋的4 m口径天线反射面型面误差RMS2值可达1.0 mm以下。

3)此类结构的研究尚处于起步阶段，今后将对考虑反射面张拉反枕效应的型面精度控制、弹性肋弯曲变形中的扭转问题、含有大变形构件的展开运动过程、结构的索力分布与动力学性能等方面展开详细研究。