天宫二号组合体与伴星有效迎风面积的一种分析计算模型

韩 意，陈 明，张 宇，孔 静，段成林

1 引言

在空间实验室任务阶段，各航天器有效迎风面积参数是否准确，直接影响航天器大气阻力建模、精密定轨以及轨道预报精度[1]。2016年9月15日天宫二号及其搭载的伴星发射入轨，10月19日神舟十一号在393 km轨道与天宫二号交会对接构成组合体，以三轴对地定向的模式飞行(下文简称正飞)。10月23日伴星从天宫二号上成功释放[2]。在10月23日至11月15日共计约24天的时间里，伴星与组合体共同运行在平均高度约388 km的轨道上。与历次载人航天工程任务相比，这是首次有2个航天器长时间运行在相同轨道高度，对各目标精密定轨中大气阻力系数求解提供了一致性对比的条件。天宫二号组合体等大型航天器外形复杂，且姿轨运动形式多样，不同部件之间存在遮挡关系，难以准确计算其迎风面积。我国即将建造的空间站也飞行在相近轨道高度上，由于尺寸结构以及构型更加复杂，其迎风面积计算难度更大。研究该高度大气阻力特点及航天器迎风面积计算方法，对于提高空间站定轨预报精度具有重要意义。

国内外研究人员在航天器迎风面积与阻力系数CD分析方面开展了相关研究[3]，卢伟[4]提出了迎风面积包络微元计算法，解决了具有规则表面形状卫星的迎风面积精确计算问题；杨成等[5]采用了基于阴影图计算迎风面积的方法；朱战霞等[6]提出了以微元划分思想建立航天器三维网格模型、使用射击线扫描法求解迎风面积的方法，计算结果与参考值误差在10%以内；刘卫等[7]从小波分解的角度分析了卫星阻力系数与空间环境参量变化的关系，为CD预报提供了方法；Mehta等[8]采用了一种响应面模型方法来研究航天器的阻力系数，分析了球体、GRACE卫星和哈勃望远镜以及国际空间站阻力系数的建模情况。

本文根据组合体和伴星的精密定轨需求，采用一种基于开放式图形库OpenGL和3ds格式三维模型的迎风面积计算方法，开发工具软件，给出正飞与连续偏航2种状态下的迎风面积计算方式，解决复杂结构航天器有效迎风面积计算困难的问题。

2 大气阻力模型分析

除地球非球形摄动力之外，大气阻力是影响低轨航天器轨道确定与预报精度的最主要的摄动力[9-10]。根据自由分子流理论，大气分子与航天器表面撞击后会发生阻留、漫散射、镜反射等运动，大气阻力的一般模型为式(1)[1]。

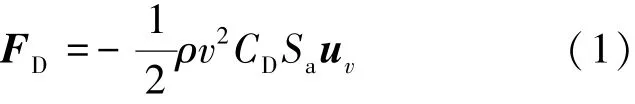
式中，FD为大气阻力，ρ为航天器所处位置的大气密度，v为航天器相对大气的速度大小，uv单位速度矢量，CD为大气阻力系数，Sa为有效迎风面积，微积分计算公式如式(2)所示。

式中，d s为航天器表面在速度方向上的有效微平面元，θ为该微面元法向与速度方向的夹角。

由式(1)可知，ρ、Sa和CD这3个不确定性因素是大气阻力难以精确建模的主要原因。大气密度随机性很强，各种影响因素比较复杂。目前使用的各种大气密度模型有指数模型、改进的Harris-Priester模型、DTM模型等，大都属于半经验模型，误差约为10%~20%。大气密度不仅与高度有关，还与周日项、太阳活动、地磁活动、季节、经纬度等因素密切相关[11-12]。空间环境参数主要用于计算大气密度，基本都是通过观测获得并基于相应的模型进行预报得到的。迎风面积分析是从航天器自身角度出发，计算其在飞行方向上的有效截面积。通过准确获取空间环境参数和计算航天器有效面积，有助于提高测定轨精度以及轨道预报的精度。航天器飞行过程中姿态在不断变化，迎风面积也随之变化。在定轨中对迎风面积的处理通常有2种方法，一是将航天器表面积的1/4作为有效迎风面积值，二是将迎风面积作为未知参数与轨道状态参数一起进行估计。这2种方法都是近似处理，精度不高。实际应用中为便于计算和提高估计的准确度，通常将航天器设计为对称体或姿态容易掌握的小面质比的构型[4]。

鉴于CD的准确数值难以确定，因此在精密定轨中可先计算出目标迎风面积，然后把CD作为未知量与卫星运动状态矢量一起解算，求解的CD一定程度上补偿了由于大气密度的模型误差所导致的大气阻力的误差，能够使动力学模型和观测数据更好地拟合，从而得到更高的内符合精度[13]。

3 有效迎风面积计算方法

3.1 基于OpenGL的计算方法

天宫二号、神舟十一号组合体和伴星的三维模型分别如图1所示，图中oxyz为各自的本体坐标系，正飞时oz轴指向地心。从图中可以看出，伴星结构较为简单，而天宫二号与神舟十一号结构复杂，迎风方向上各部件之间存在相互遮挡关系。

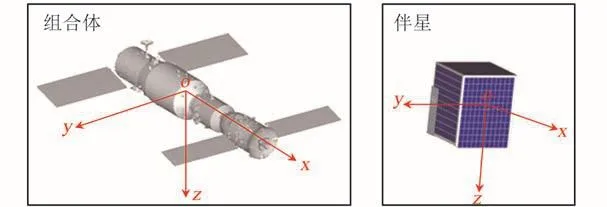
图1 组合体和伴星三维模型Fig.1 3D models of complex and accompanying satellite

采用微元划分思想计算目标迎风面积时，需要3个步骤：目标三维建模与细分、读取和处理模型、面积计算。首先需要将目标细分为许多个微小平面面元，并计算每个小面元的顶点坐标、法向矢量和材质类型，判断出有效迎风的小面元，还要判断面元的相互遮挡关系，将被遮挡的面元剔除掉，之后计算有效面元的面积，最后通过累加方式得到整个目标的迎风面积。

上述过程中，所需目标模型可以通过三维建模获得，每个面元对应的θi也可通过数值计算获得，但面元之间相互遮挡关系的判断则比较复杂，需要多次循环计算和比较。通过软件编程执行循环计算和判断，比较费时且精度较低，尤其对于复杂目标，面元划分越细则面元数量越多，计算时间呈指数级增加。但若减少面元数量、增大面元面积，相互遮挡关系的判断误差则大幅增加，计算精度降低。

OpenGL提供了强大的图形函数将大量数据转换成图形或图像在屏幕上显示出来并可进行交互处理，即快速可视化功能。此外OpenGL在深度缓存中为每个像素存储了该像素与视点之间的深度值，可以通过启用深度缓冲区和深度测试，利用计算机图形加速卡在硬件层级迅速实现目标消隐。

为解决计算效率及精度与面元细分和遮挡判断之间的矛盾，采用一种基于OpenGL的有效迎风面积计算方法，利用OpenGL的可视化与消隐功能开发了工具软件，能够计算航天器在任意姿态下的有效迎风面积，每次用时小于0.05 s，速度快、效率高，可用于飞行试验任务中面积实时计算的场合，其基本流程如图2所示。

1)根据工业部门提供的航天器模型文件，使用三维建模软件3DSMAX进行模型格式转换、编辑、加工和处理，用不同的材质表示和区别航天器不同部件和载荷(舱体、太阳能电池帆板和天线等)，设定材质对光源的散射特性是漫反射。

2)通过软件编程读取3ds格式目标模型文件。面积计算需要用到目标表面各点位置、法线方向、面元面积、面元所在的材质种类等数据。3ds文件格式是一个由块组成的层级结构，基本块即主块包括版本、编辑信息和关键帧信息等，每个基本块中的一级块又包含了多种信息。需要读取的模型数据包括目标对象材质信息、顶点信息和面元信息等。本文将其读入到自定义数据结构之中，然后利用OpenGL绘制目标模型。

图2 迎风面积计算流程示意图Fig.2 Flowchart of windward area calculation

3)根据当前时刻目标姿态对三维模型进行旋转变换，应用OpenGL的可视化与消隐功能，采用正交投影模式将三维目标投影到二维屏幕并启用深度缓冲区进行深度测试，并完成复杂目标的消隐和可见部位的显示，提高了计算的准确度和速度。

4)采用Phong光照模型，通过设置合适的参数，读取光照渲染处理后的帧缓存中的像素面元颜色值，得到各个面元的法向矢量、各面元与速度方向的夹角以及面元所代表的部件种类等参数信息，从而计算各面元迎风面积，最后通过累加计算出整个目标的迎风面积。

设置光源为方向漫反射白光源，强度为1。设第(i，j)个像素面元的单位法矢为n，面元材质属性为Cm=(R，G，B)，速度方向单位矢量为l，设θij为n和l的夹角，则显示区域上该像素的颜色值为式(3)。

通过读取目标模型可见部分每个像素的颜色值Iij及其组合方式，可计算出面元法向与速度方向的夹角θij以及面元材质种类。设该像素对应的目标面元的实际面积为s0，其有效迎风面积为sij为式(4)。

根据式(2)，通过计算各面元迎风面积sij的代数和，可得到整个目标的迎风面积Sa，即式(5)。

为检验上述方法的准确性，以长方体为目标开展比对验证实验。如图3所示，建立一个长方体模型，其长度为l，宽度为w，高度为h，长方体绕坐标系o-xyz的oy轴做顺时针旋转，旋转角度用θ表示(对应于航天器本体的偏航转动)，速度方向与ox轴相同，图中是θ=0°时的姿态情况。

图3 长方体及其迎风面积计算结果Fig.3 Calculation results of the cuboid and effective windward area

对于任一旋转角θ，长方体有效迎风面积Sa的理论值为式(6)。

当 l=1.5 m，w=1.0 m，h=2.0 m，θ从 0°以0.5°的间隔增加至180°时，根据式(6)计算的Sa理论值、本文方法计算的迎风面积与理论值之间的偏差如图3中曲线图所示。

该长方体Sa的理论值范围为2.0~3.547 m2，本文的计算结果与理论值的偏差小于0.005 m2，相对偏差小于0.2%，表明了本文方法的正确性。

3.2 正飞与偏航时迎风面积计算方式

大型航天器正飞时以三轴稳定的方式在轨运行，其偏航、俯仰、滚转角基本为0，只有太阳电池板根据太阳与轨道面的夹角转动。为补偿大气密度建模误差，在精密定轨时使用3圈以上弧段，弧长6 h、9 h、12 h，则该时间段有效迎风面积S0可认为是太阳翼转动一圈的平均迎风面积与本体最大截面积之和。航天器连续偏航时，其迎风面积则难以用数学表达式来描述。

如图4所示，设太阳翼的宽为w，高为h，面积A0=wh，初始状态时太阳翼与速度风向(迎风方向)垂直，绕旋转轴转动一周总共需要转动N次，转到第i次(i=1，… N)时与初始状态的夹角为θi，这时的有效迎风面积Ai如式(7)所示。

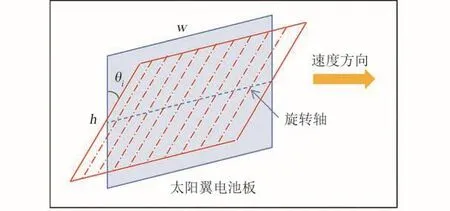
图4 太阳翼电池板转动示意图Fig.4 Schematic diagram of solar panel rotation

则太阳翼转动N次的平均迎风面积为式(8)。

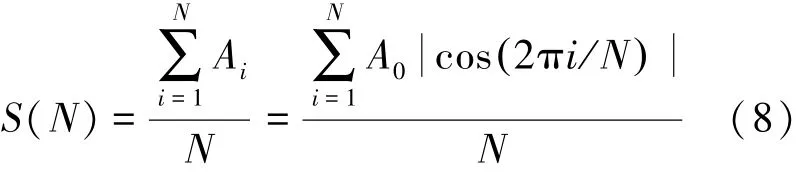
当N趋向于无穷大时，这时的S(N)即可认为是太阳翼转动一周的迎风面积S，如式(9)所示。

使用积分函数来表示上式，设x=2πi/N，则d x=2π/N，因此可得式(10)。

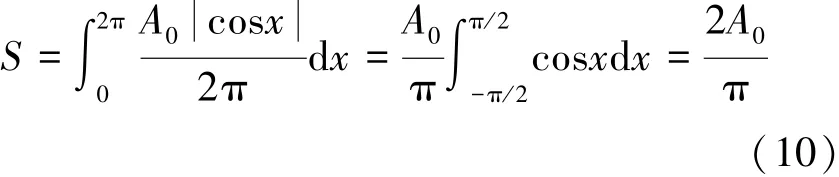
则航天器正飞状态下的有效迎风面积S0为式(11)。

式中，A0为航天器太阳翼(包括电池片和支架)的面积，S2为航天器舱体及外部载荷的截面积。

对于天宫二号与神舟十一号，单体正飞时可用式(11)直接估算其迎风面积，而二者对接而成组合体后，正飞时由于两个舱体尺寸结构不同，且各自太阳翼存在前后遮挡关系，因此组合体的迎风面积无法直接根据式(11)计算，需要使用本文的工具软件采取不同的计算方式，具体如下：

1)正飞状态时，保持航天器模型本体不动，太阳翼绕旋转轴等间隔转动0.05°或更小，累计转动7200次，将各次计算的迎风面积求平均值，即可认为是正飞状态下的迎风面积；

2)连续偏航时，需要读取定轨所使用的测量弧段内航天器偏航角和太阳翼转动角度等姿态参数文件，计算各个时刻对应的迎风面积，然后取平均值作为该偏航弧段内的有效迎风面积。

4 实际定轨解算情况

在天宫二号与神舟十一号飞行任务中，利用各航天器的地基、天基测量数据并考虑轨控影响进行精密轨道确定，计算和预报各目标在过去、当前和未来一段时间的运动状态(包括星历和姿态参数)[11]，轨道确定位置误差优于10 m量级。

任务中测定轨采用MSIS90半经验大气密度模型，主要使用当日地磁指数日均值Ap、前1天10.7 cm太阳辐射流量日均值F10.7和81天10.7 cm辐射流量平均值F10.7p等空间环境参数[14]。参数来源为每日国家空间科学中心提供的空间环境参数值及3天预报值。该模型在空间实验室任务阶段应用效果良好[15]。

从10月23日07：31至 11月 15日 12：00约24天的时间里，伴星与组合体均以正飞的方式运行在高度约为388 km的轨道上，期间两目标每天早8点的相对距离变化情况如图5所示，相对距离范围为0~280 km，但平均轨道高度相差在2 km以内。

图5 组合体与伴星相对距离变化情况Fig.5 Changes of relative distance between the complex and accompanying satellite

24天里的空间环境参数变化情况如图6所示。除10月27日发生一次较为明显的磁暴外，整个过程中空间环境比较平静，太阳活动稳定，F10.7变化不大，均值在77左右。

图6 空间环境参数变化情况Fig.6 Changes of space environment parameters with time

在迎风面积参数方面，最初计算时只考虑了舱体最大直径和太阳翼电池板的尺寸，与实际情况有一定偏差。本文根据各目标的精细三维模型，综合考虑了舱体及舱外载荷和零部件、太阳翼厚度及支架的尺寸等来计算迎风面积。伴星和组合体精密定轨时使用了3整圈以上的相同的数据弧段，其空间环境参数一致。设使用原先方式计算的组合体正飞时的迎风面积为M1、伴星面积为N1，使用本文方法计算得到组合体迎风面积为M2、伴星的面积为N2，在10月23日至11月2日期间，每天1~2次的两目标相同弧段精密定轨中，分别使用M1、N1求解得到的大气阻力系数CDm1、CDn1及二者之差，分别使用 M2、N2求解得到的大气阻力系数CDm2、CDn2及二者之差，具体如表1所示，表中序号表示不同的定轨历元时间。

从表1中可以看出，使用原先面积参数时两目标分别解CD值相差较大，差值基本在0.2~0.35，均值为0.26；使用本文方法计算出的面积参数后，两目标CD相差约为0.01~0.07，均值为0.03。

从11月2日至11月15日期间，每天1~2次的两目标同弧段精密定轨时，分别使用M2、N2求解得到的大气阻力系数CDm2、CDn2及二者之差如表2所示，伴星求解CD均值为2.033，组合体解CD均值为2.026，两目标CD之差小于0.01。

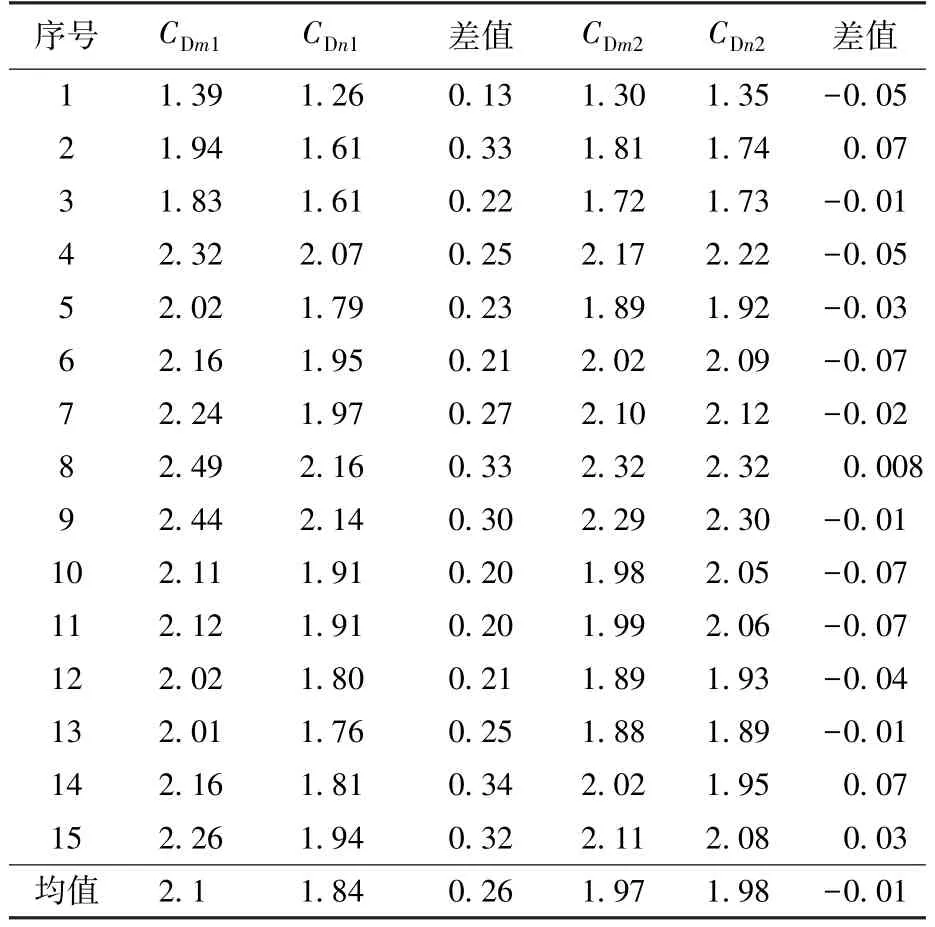
表1 伴星和组合体定轨求解C D结果对比(10月23日—11月2日)Table 1 The first group of C Dcomparisons of the complex and accompanying satellite(Oct.23-Nov.2)

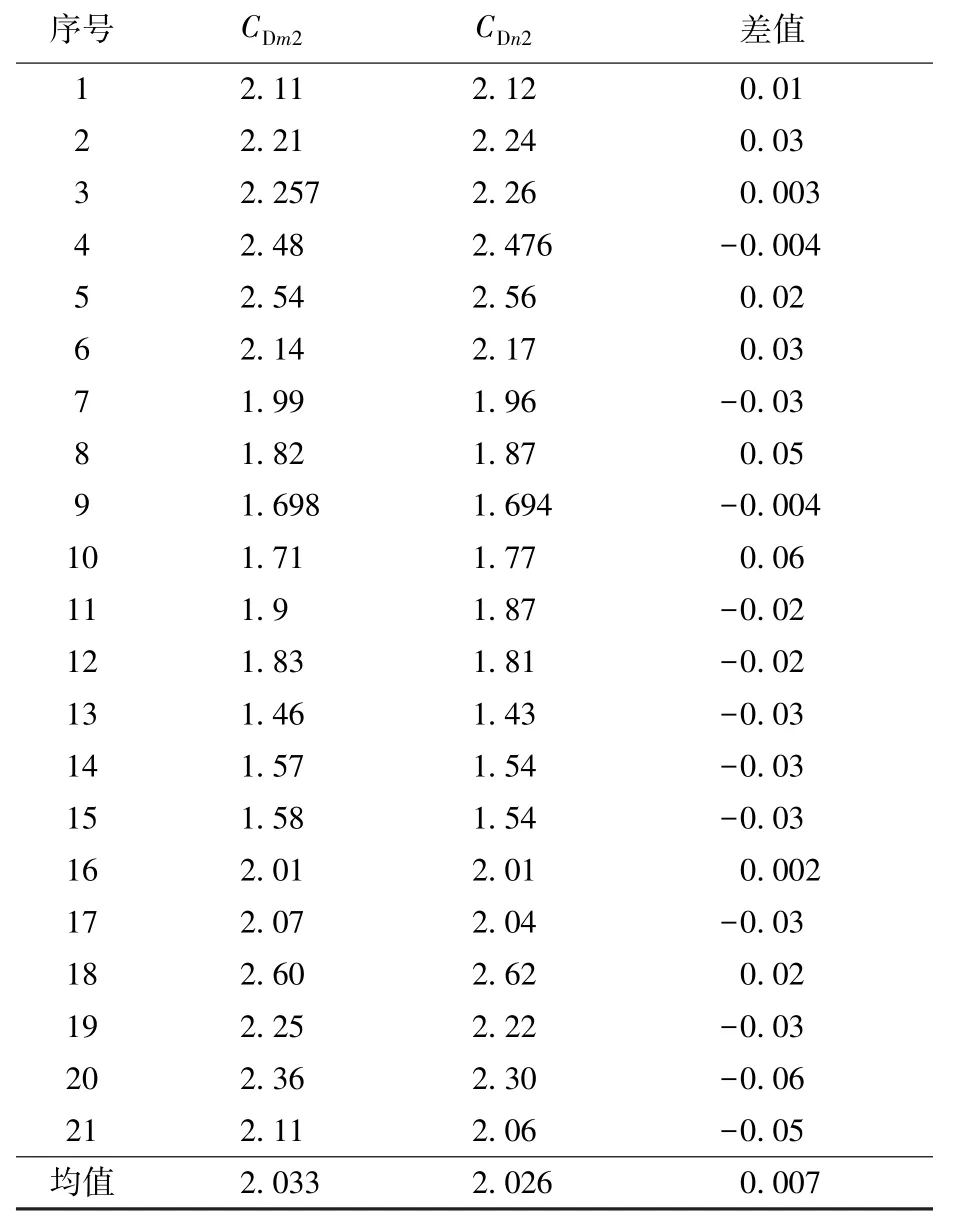
表2 伴星和组合体定轨求解C D结果对比(11月2日—11月15日)Table 2 The second group of C D comparisons of the complex and accompanying satellite(Nov.2—Nov.15)

理论上相同轨道、相同表面材料、相同形状的两目标精密定轨求解的大气阻力系数结果应当相同。由于组合体与伴星轨道高度接近、二者有效迎风面为平面，且迎风面材质大部分是太阳能电池片，因此二者求解的大气阻力系数结果应当相近。根据表1和表2可以看出，使用本文方法计算出的迎风面积参数，两目标精密定轨求解大气阻力系数结果一致，与理论分析相符合。

5 结论

本文采用一种基于OpenGL和3ds格式三维模型的大型复杂结构航天器迎风面积计算方法，给出了正飞与连续偏航2种状态下的迎风面积计算方式；根据组合体与伴星共同正飞的24天里的精密轨道确定结果，求解得到的两目标大气阻力系数十分接近，二者之差约0.01~0.07。此外，两目标定轨结果表明388 km轨道高度的CD平均值约为2.0，与传统使用的CD值2.2有一定的差异，进行轨道预报时CD值使用2.0比2.2的精度更高。

与其他方法相比，本文方法和软件具有自主知识产权并经过了实际航天任务的数据验证，重点针对大型航天器，目标三维模型与材质模型的精细化程度更高，具有一定的工程实用价值，并且便于开展大量仿真分析实验。后续将根据实际需求进行功能扩展和升级，为载人空间站任务航天器有效面积计算、所在轨道高度大气阻力特性研究提供参考和支持。