基于IMM-UPF的锂电池寿命估计

刘新天，张恒，何耀，郑昕昕，曾国建

（合肥工业大学汽车工程技术研究院，安徽合肥230009）

锂电池因其具有高能量比、高效率、循环寿命长等显著特点，而成为未来电子市场的首选电源[1].与铅酸电池和镍氢电池相比，锂电池因为可高温存储、快速充电、输出功率大且没有记忆效应等优点在车辆和固定式动力系统中得到广泛应用[2].

作为电池管理系统（Battery Management System，BMS）的核心环节之一[3-4]，健康状态（State of Health，SOH）因为能够提供准确的数据，达到延长电池使用寿命的目的，因此在电池使用方面发挥着至关重要的作用.然而，由于电池使用期间伴随着复杂的物理和化学反应，锂电池的性能在使用一定时间后以非线性的形式恶化[5]，这就给锂电池状态的预测带来了很大的不确定性[6].

目前，锂电池状态估计的方法可以分为3大类：基于物理原理建模法[7-11]、基于数据建模法[12-15]和两者相结合的方法[16].基于物理原理建模法通常通过建立物理模型和经验模型来描述锂电池的物理和失效机制，然后建立相应的数学函数.Tsang等人[17]对锂电池等效直流电阻的测量开发了锂电池SOH的估算方案.Ning等人[18]根据负极内的不可逆电化学反应和正电极的氧化反应，建立了SOH估算模型.Singh等人[19]开发了一种基于模糊逻辑的锂离子电池SOH估算方法，其中电化学阻抗谱（Electrochemical Impedance Spectroscopy，EIS）测量值作为模糊逻辑模型的输入量.

基于物理原理建模的方法在有些时候可以准确地预测容量衰减.然而，对于复杂的动态系统，特别是具有不确定噪声的系统，通常很难建立精确的分析模型，更不用说这些模型通常局限于特定锂电池类型.另一方面，基于数据建模的方法可以捕捉数据中的内在关系并学习数据中所呈现的变化趋势，而不需要材料特性、结构、失效机制等方面的具体知识，避免了开发过于复杂的物理模型，使得它比基于物理原理建模的方法更易于实际操作.

近年来，由于对物理失效机制的依赖性较小，基于数据建模的方法得到了广泛的研究.例如，Guo等人[20]研究了一种新的贝叶斯方法，可以在不同的条件下对锂电池的剩余寿命（Remaining Useful Life，RUL）进行准确预测.Miao等人[21]提出了一种改进无迹粒子滤波（Unscented Particle Filter，UPF）算法，该算法能够准确地预测锂电池实际剩余寿命（RUL），预测误差小于5%.He等人[22]使用d-s证据理论和贝叶斯蒙特卡洛方法对经验模型进行剩余寿命（RUL）预测.

基于数据建模的方法因具有简单易操作的特点，应用较为广泛.考查锂电池的整个寿命周期，容量衰减趋势可分为两个阶段：第一阶段为缓慢衰减阶段，SOH衰减速度缓慢且时间较长；随后是快速衰减阶段，SOH的值迅速下降且用时较短.因此，常用的单一经验模型可能在不同阶段取得很好的预测效果，但是无法很好地描述锂电池的整个寿命周期的变化趋势.同时，经验模型的初始参数确定需要大量的实验数据，意味着在样本数量不多的情况下，对锂电池的剩余寿命（RUL）预测将产生较大误差.为了解决这些问题，本文提出了一种新的融合模型交互式多模型（Interacting Multiple Model，IMM），用于对不同的衰减模型融合计算.与经典的IMM使用卡尔曼滤波（Kalman Filter，KF）不同，考虑锂电池衰减呈现非高斯和非线性的趋势使用卡尔曼滤波存在较大的误差，本文拟使用无迹粒子滤波（UPF）对各模型进行滤波，一方面解决了粒子滤波（Particle Filter，PF）在重采样过程中粒子贫化的问题，另一方面又比卡尔曼滤波得到了更准确的预测结果[23].最后通过仿真结果和实验数据对比的方法对本文提出的IMMUPF方法进行了验证，结果表明该方法可以实现对剩余寿命（RUL）较准确的预测.

1 容量衰减模型

1.1 锂电池容量测量

本文使用的实验数据来源于马里兰大学高等生命周期工程中心（CALCE）[24].

实验所用的锂电池额定容量为1 100 mA·h.4个电池都遵循相同的标准恒定电流/恒定电压协议：首先以恒定1 C电流充电，直到电压达到4.2 V，然后以4.2 V恒压充电，直到充电电流降至0.05 A以下后，结束充电.在室温下（25℃）进行充放电实验，记录每一次完全充放电过程后的放电容量.容量衰减曲线如图1所示，电池的失效阈值（Failure Threshold，FT）设为880 mA·h（即SOH=80%时对应的电池容量）.

在本文中，有4组容量数据A1、A2、A3和A4，如图1所示，图中每一条线代表电池最大可用容量和循环次数之间的关系.与A1、A2和A3电池相比，A4与其他电池存在较大的差异性，为了验证本文方法的准确性，电池A1、A2、A3的数据将用于确定各单一模型参数的初始值，A4电池的数据将被用来对本文方法预测准确性的验证.

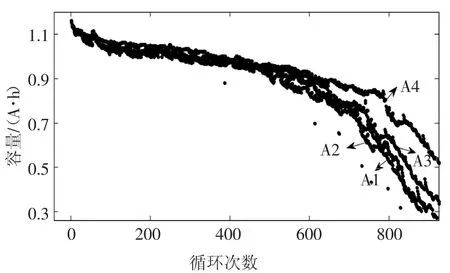
图1 容量衰减曲线Fig.1 Capacity decay curve

1.2 多项式模型

Micea等人[25]提出一种由最小二乘法来估计电池容量Ck的二阶多项式回归方程.方程描述了锂电池在循环次数k与可以存储的最大容量Ck之间的关系，多项式的表达式为（模型1）：

式中：Ck表示锂电池在循环次数k时的电池容量；k表示锂电池循环次数；参数a、b和c都是与放电电流I和温度T有关的常数，可以通过曲线拟合确定取值.

电池A1的容量数据以及对应方程（1）的曲线拟合结果（实线）如图2所示.利用MATLAB中的曲线拟合工具对模型参数进行估计.为了考查该模型是否适用于测试实验对象，将拟合优度作为模型拟合度好坏的评价指标.若曲线拟合良好，则根均方误差（Root Mean Square Error，RMSE）将接近0，而决定系数（Coefficient of Determination，一般称为R2）将接近1.

图2 模型1对A1电池的曲线拟合Fig.2 The curve fitting of the model 1 to the battery A1

1.3 指数模型

Goebel等人[26]用两个指数函数之和来描述固体电解质界面膜（Solid Electrolyte Interphase，SEI）随时间的增厚引起的内阻抗增加.由于电池容量衰减主要与内部阻抗增加有关，容量衰减的模型也可用指数模型来描述.文献[27]采用MATLAB曲线拟合工具，基于最小二乘法估计方法，建立了用双指数方程（2）表示的经验模型（模型2），此模型能够较好地拟合锂电池寿命的衰减过程.

式中：Ck表示锂电池在循环次数k时的电池容量；k表示锂电池循环次数；参数a和b是与内部阻抗有关的常数；参数c和d是和电池老化速率有关的常数.a、b、c和d的值可以通过曲线拟合确定.

式（2）关于电池A1的容量数据的曲线拟合结果（实线）如图3所示.

图3 模型2对A1电池的曲线拟合Fig.3 The curve fitting of the model 2 to the battery A1

1.4 集成模型

Xing等人[28]开发了一种融合模型1和模型2的集成模型，该模型可以很好地拟合部分数据，有较好的全局拟合优度.公式为（模型3）：

式中：Ck表示电池容量；k表示循环次数；参数a、b、c和d可用MATLAB中的曲线拟合工具求得.式（3）关于电池A1的容量数据的曲线拟合结果（实线）如图4所示.

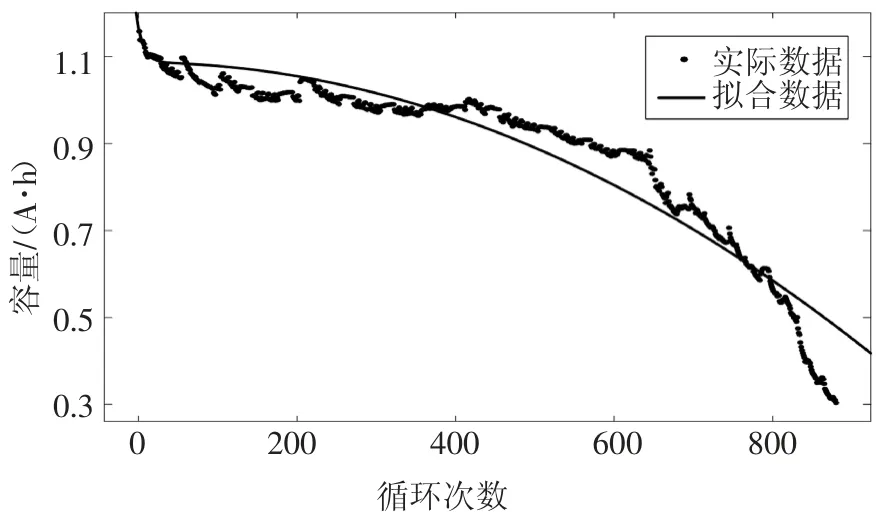
图4 模型3对A1电池的曲线拟合Fig.4 The curve fitting of the model 3 to the battery A1

表1显示了电池A1关于3个模型的拟合参数值，包括95%置信区间的上下限.表2显示了A1、A2和A3电池对应各模型的拟合参数值.表3显示了3节电池基于3种模型的拟合优度统计.

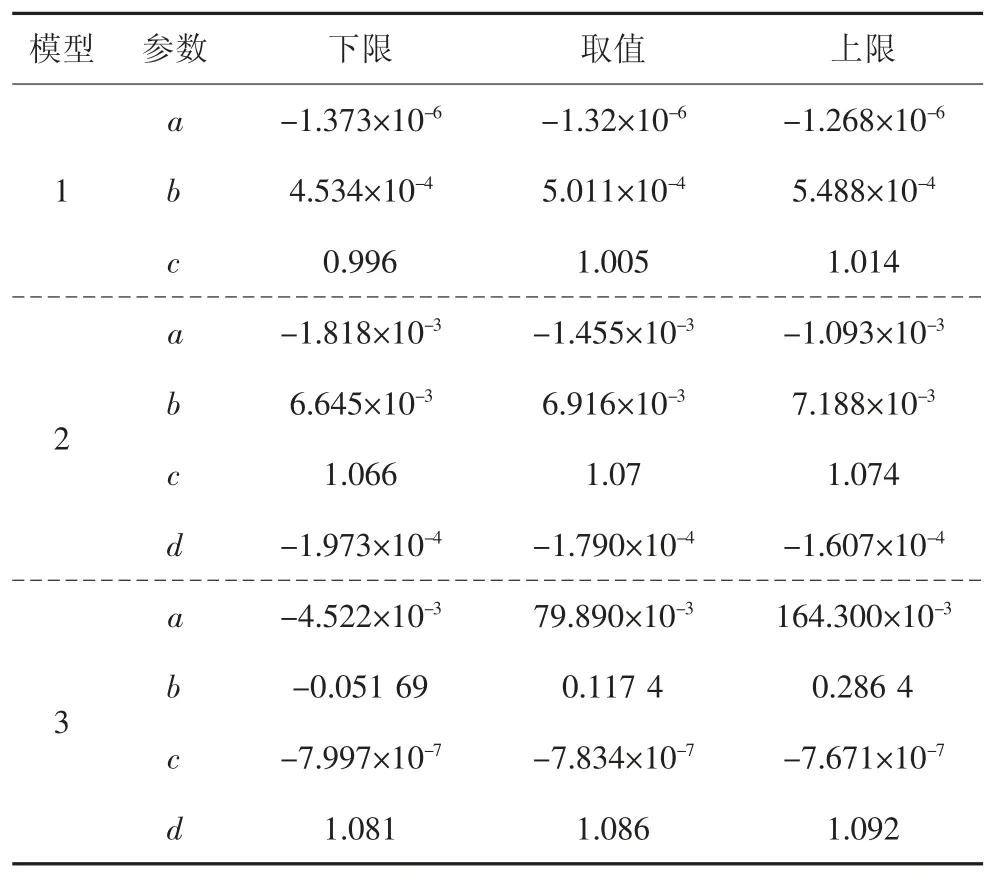
表1 A1拟合参数值（包括95%置信区间）Tab.1 Fitted parameter values for A1（bounds for the 95%confidence intervals included）

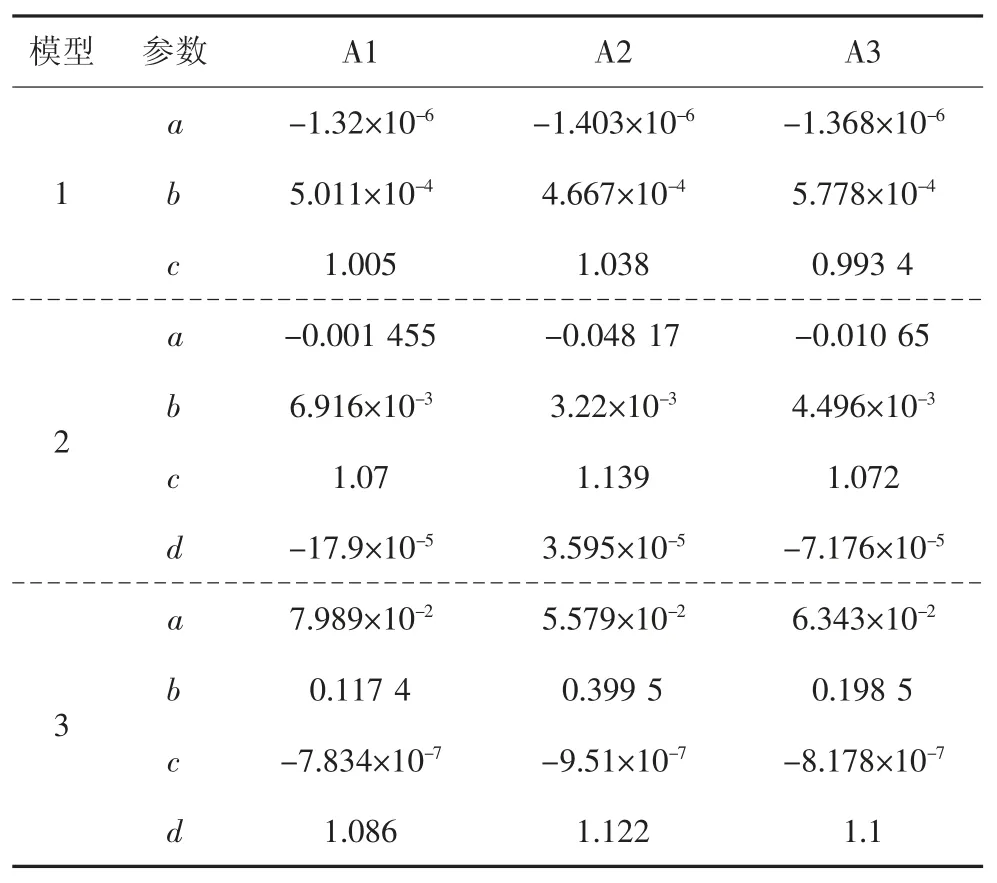
表2 A1、A2、A3电池的3种模型拟合参数值Tab.2 Fitting parameters of three models for battery A1，A2 and A3

表3 拟合优度统计Tab.3 Goodness-of-fit statistics

2 交互式多模型无迹粒子滤波器

2.1 无迹粒子滤波器

粒子滤波是一种将贝叶斯学习技术与重要性采样相结合的递归估计方法，也被称为序贯蒙特卡罗方法.对于给定系统：

式中：x为状态向量；Z为测量向量；Wk为过程噪声；Vk为测量噪声.假定观测量Zk独立于给定当前状态量xk的其他状态.

PF算法的关键是用一组具有相关权重的粒子表示概率密度函数（Probability Density Function，PDF）：

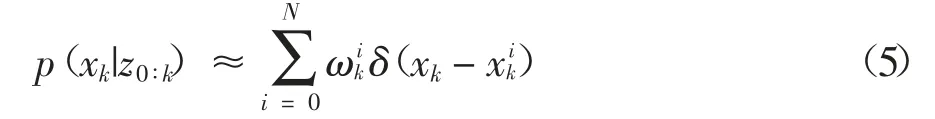
UPF算法的实现步骤如下：

1）初始化.对应方程（4）的系统，周期为k的方程为：

2）Sigma采样和权值计算.

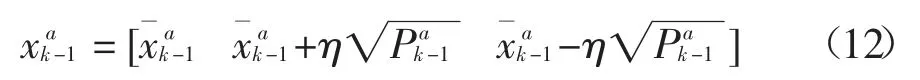
其中n=nx+nV+nW表示状态量、过程噪声和测量噪声的维数之和.相应的权重为：

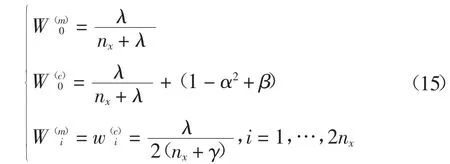
3）预测函数的更新.

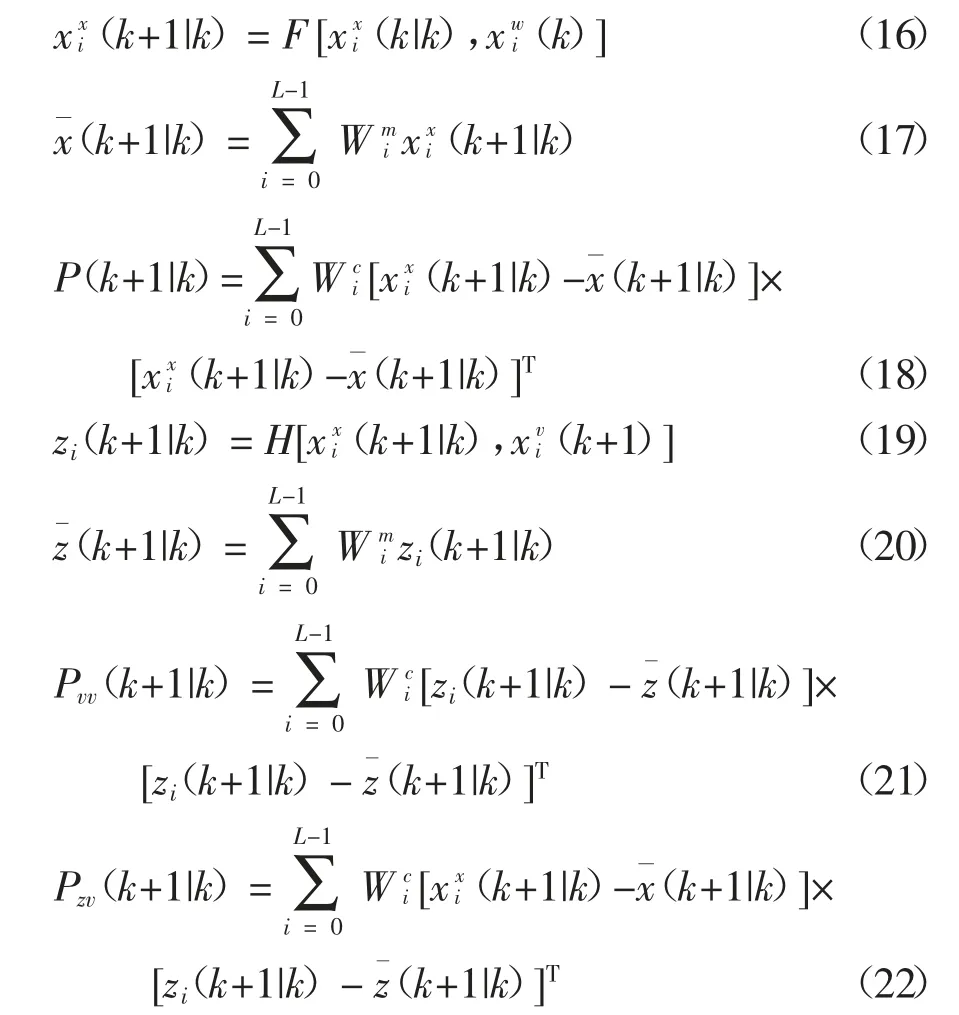
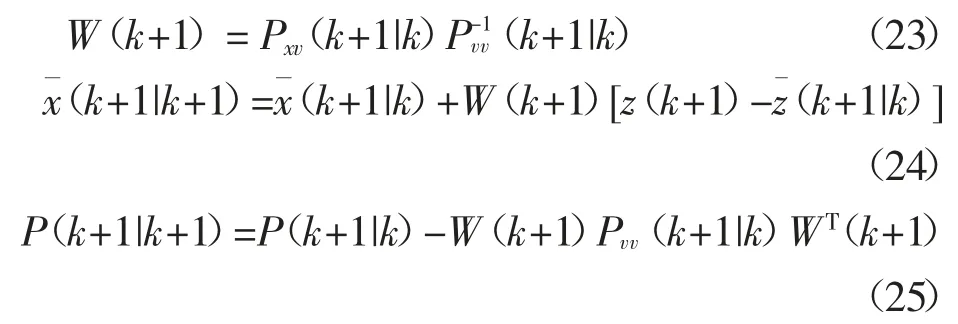
4）权值计算和重采样.

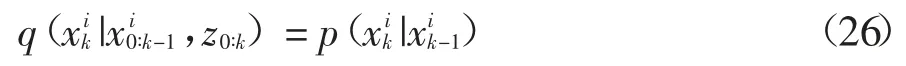
权重值可以由如下公式确定：

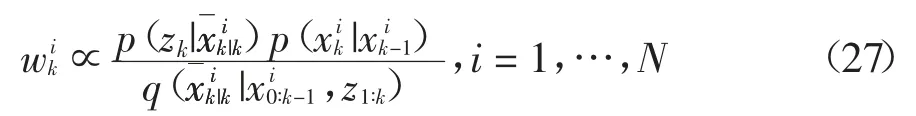
权重标准化：

重采样：当Neff的值小于阈值Nth时，进行重采样，阈值Nth通常设为Nth=2N/3.Neff可由以下计算式得到：

状态量和对应的协方差为：

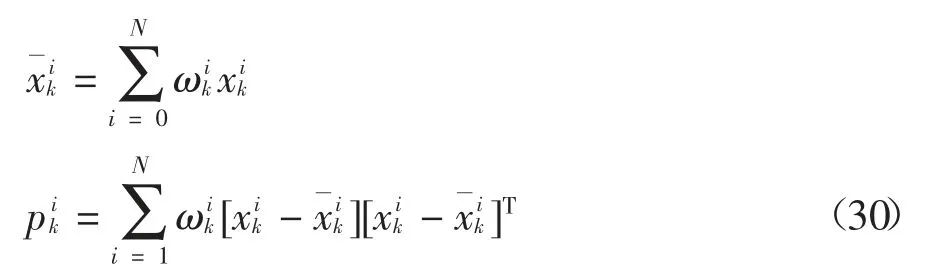
2.2 交互式无迹粒子滤波

IMM-UPF不仅可以处理非线性和非高斯噪声，而且可以对系统的状态进行准确的估计[29].

IMM-UPF有4个主要步骤：

1）输入交互.对于模型j，周期为k时：

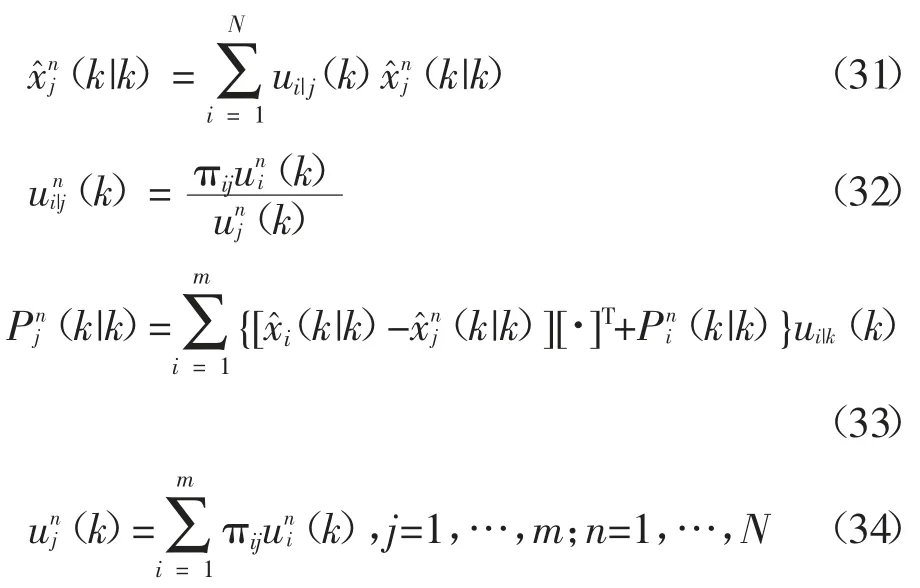
2）滤波.对于模型j，粒子将用UPF进行滤波，利用周期k的粒子集得到下一周期k+1的状态及其协方差的估计量和，残差及其协方差为.

3）更新.原有的概率将被更新，新的混合概率将根据其似然函数进行计算.对于模型j，其似然函数可以写成：

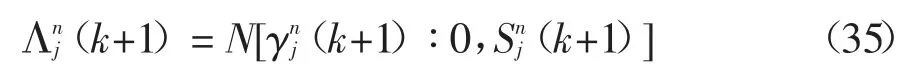
其中N[·]表示服从高斯分布的密度函数.新的混合概率表示为：

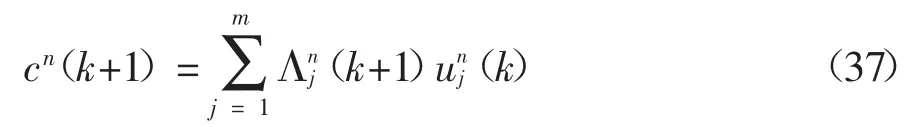
4）输出交互.表示状态及其协方差的粒子集将通过下列函数实现交互：

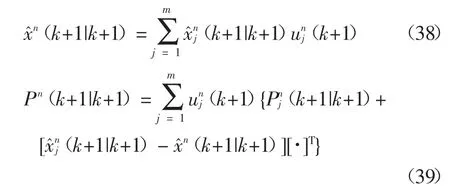
最后状态量及其协方差以下列方式输出：

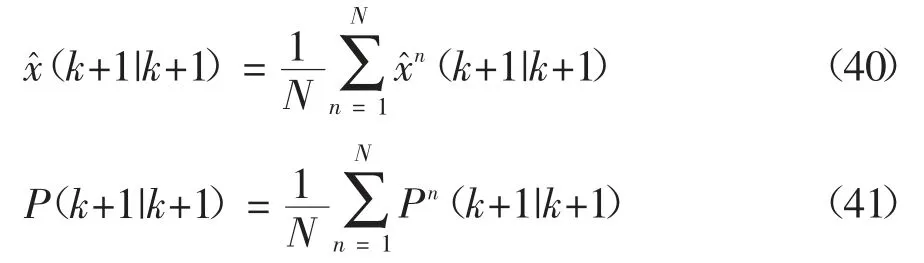
周期为k时交互式多模型无迹粒子滤波器的流程图如图5所示.

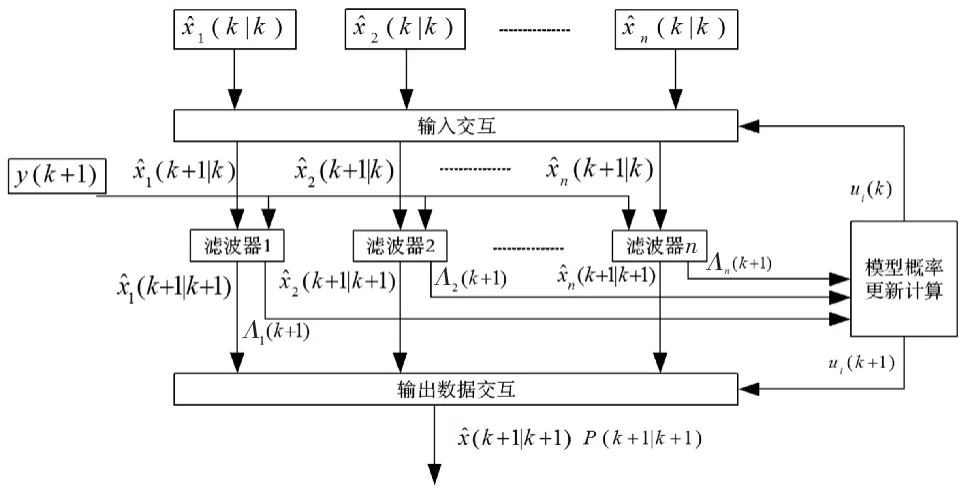
图5 IMM-UPF流程图Fig.5 The flowchart of the IMM-UPF

3 实验结果与分析

3.1 初始参数与状态方程确认

为了验证交互多模型在提高预测精度上的有效性，本文进行了2个案例研究.1）A4电池对应各模型的初始参数可以由另外三节电池A1、A2和A3得到.当训练数据TD=300时，各模型分别使用UPF算法来预测A4电池的剩余使用寿命，结果分别如图6、图7和图8所示.2）利用交互式多模型对A4电池的实际数据进行滤波和参数更新，3个模型在每个周期的状态量和协方差在IMM中实现输入和输出交互.IMM-UPF的预测结果如图9所示.假设A1、A2和A3的拟合参数值均可信，基于不同电池的参数值的初始基本置信分配可以由如下公式确定（以各模型参数a的置信度为例）：

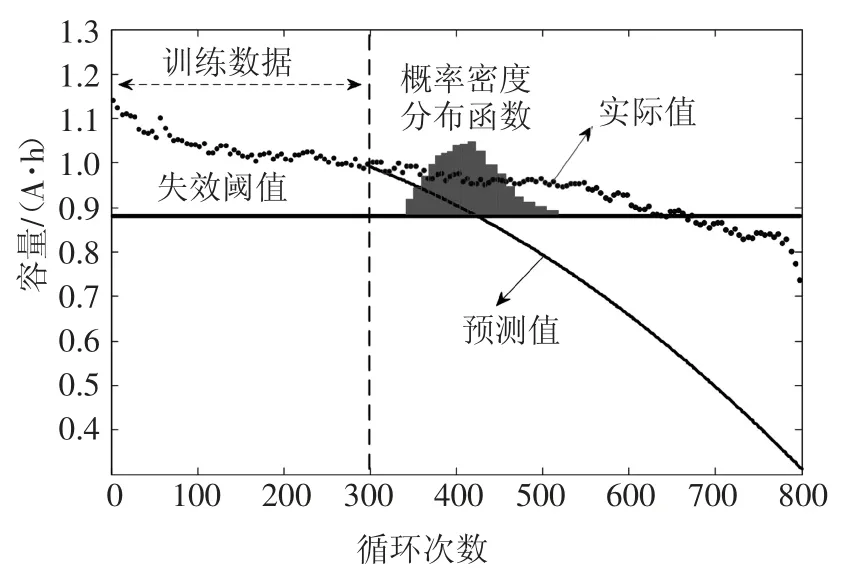
图6 TD=300时，模型1使用UPF算法的仿真结果Fig.6 TD=300，simulation results of model 1 using UPF algorithm

图7 TD=300时，模型2使用UPF算法的仿真结果Fig.7 TD=300，simulation results of model 2 using UPF algorithm

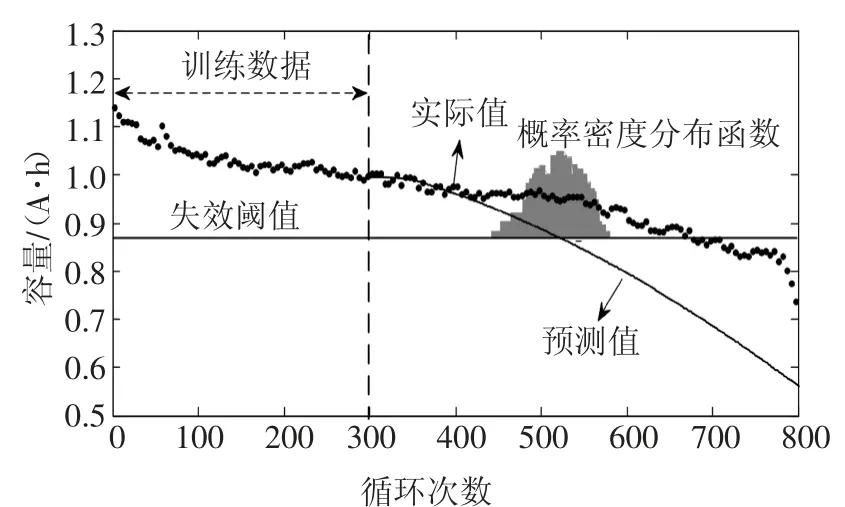
图8 TD=300时，模型3使用UPF算法的仿真结果Fig.8 TD=300，simulation results of model 3 using UPF algorithm

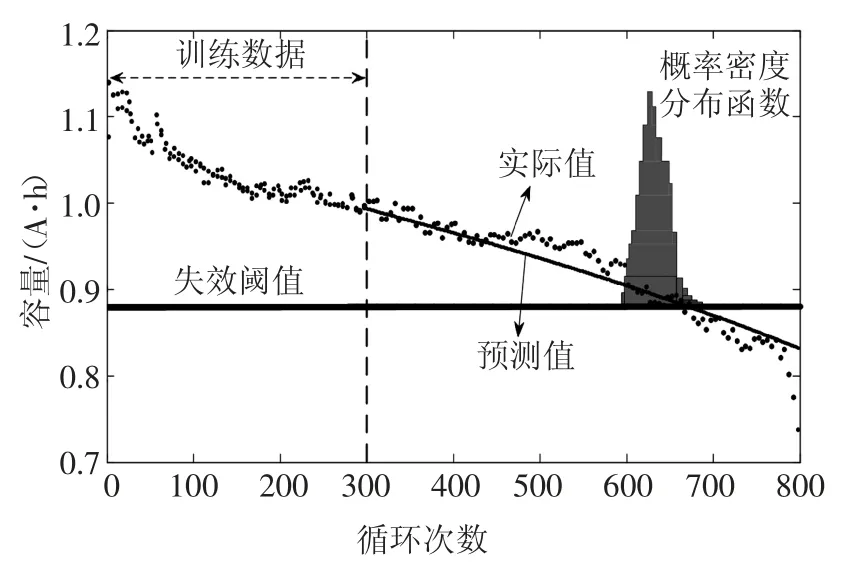
图9 TD=300时，A4电池使用IMM-UPF算法的仿真结果Fig.9 TD=300，simulation result of battery A4 using IMM-UPF algorithm

其中实验样本有3组，即电池A1、A2和A3，所以n=3.由此，模型的初始值为：

根据初始值唯一确定的假设，随着样本数据的增加，初始参数的估计值越接近真实值.

为了实现IMM的对输入量的交互作用，需要将3个模型的状态量均设为电容量Ck，以双指数型2为例，状态方程可以写成如下形式：

对应的测量方程为：

其中x（k）表示在循环次数为k时的电池可用最大容量预测值；y（k）表示循环次数为k时的最大容量测量值；N（0，σμ）和N（0，σv）分别表示均值为0和标准差为σ的高斯噪声；a、b、c和d为模型初始值，由式（43）给出.

3.2 仿真与实验结果分析

在仿真中，使用前300组数据作为训练数据，失效阈值为SOH=0.8，即容量Ck=0.88 A·h，电池实际寿命为665.即当=0.88 A·h时，对应的A4电池循环次数为665次.

为了验证本文提出算法的有效性，使用绝对误差和剩余寿命（RUL）概率密度函数（PDF）的标准偏差来衡量仿真结果的准确性和稳定性[30].

图6、图7和图8显示了仅使用UPF算法对A4电池的模型1、模型2和模型3的预测曲线.模型1和模型3的预测结果分别为424和530，即预测结果的绝对误差分别为241和135，RUL的标准偏差分别为48和42.模型2在SOH=0.8时的预测结果为706，绝对误差为41，RUL的标准偏差为37.

图9显示了用IMM-UPF算法得到的电池A4的寿命预测曲线.当SOH=0.8时算法的仿真结果为675，对应的绝对误差为10，RUL的标准偏差为19.

4 结论

1）通过对电池数据的采集和曲线拟合工具的使用，发现多项式模型、双指数模型和集成模型可以较好地拟合锂电池容量衰减过程.在对各模型初始参数值的确定中，发现在给定相同的样本数量时，多项式模型和集成模型预测结果误差相对较大，且稳定性较差，虽然双指数模型在剩余寿命（RUL）的预测绝对误差较小，但概率分布（PDF）的标准差较大，即预测的稳定性也较差.单一模型较难满足锂电池剩余寿命准确估计的要求.

2）交互式多模型的使用，使得预测结果不仅实现了对各模型初始参数的精确性依赖度下降，提高了实际使用时的效率和降低了成本，而且减小了预测误差，且RUL-PDF分布更窄，即预测结果更加稳定，是一种实际使用中可行的锂电池寿命预测方法.本文最后通过仿真与实验结果相比较的方法，比较了单模型使用UPF算法和多模型使用IMM-UPF算法对SOH进行估计的误差，结果表明，IMM-UPF算法减少了预测的误差，具有较好的精度，即稳定性更好.