Sharma-Tasso-Olever方程的Painlevé分析与精确解

陈南

(厦门工学院 计算机与人工智能学院，福建 厦门，361024)

在孤立子理论中，判定非线性方程是否具有可积性是非常重要的研究课题之一。目前，要给出可积性的严格定义是很困难的。一般地，说到可积性时，往往指方程具有哪种可积性。比如，可以利用反散射方法求出非线性偏微分方程的解，就称之为反散射可积，此外，还有对称可积、Lax可积、Liouville可积、C可积与Painlevé可积等等。Painlevé分析法[1-8]是证明可积性最有用的方法之一。目前，对Sharma-Tasso-Olever方程[9]的研究文献比较多。文献[10]证明了Sharma-Tasso-Olever 方程是可解的，并得到了孤子裂变和聚变的精确解，给出了与CTE有关的Sharma-Tasso-Olever方程的非局部对称性。文献[11]利用推广的齐次平衡法和Maple，推导出了方程的Bäcklund变换，找到了该方程与一些线性偏微分方程之间的关系。利用给出的变换和计算机程序Maple 12，构造了方程的大量精确显式特解。除了以常用的方式重新推导出所有已知解外，还可以得到几个全新的、更通用的、精确的显式孤立波解。文献[12]用修改的(G′/G)展开方法求出了方程的行波解。文献[13]用推广的Hirota双线性方法求得孤立子解。文献[14]提出了一种新的辅助方程方法来探究，这种方法由含有十阶非线项常微分方程构造而成。运用这种方法，得到方程的一些新的孤立波解和三角周期波解。本文用Painlevé分析的方法对Sharma-Tasso-Olever方程进行研究，证明其具有Painlevé可积性质。

1 Sharma -Tasso-Olever方程的Painlevé分析

Sharma -Tasso-Olever方程：

(1)

其中：α是常量；u(x，t)是时间变量t和空间变量x的未知函数。假设方程 (1)具有洛朗级数

(2)

形式的解。

式中：φ=φ(x,t)是时间变量t和空间变量x与未知函数。

首先进行主导项分析，令

u(x，t)～u0(x，t)φ-β

(3)

有

(4)

由主导项平衡，即最高阶导数项“uxxx”和最高阶非线性项“u2ux，uuxx”的平衡，计算得β=-1，并得到2个分支：

分支Ⅰ，u0=φx

(5)

分支Ⅱ，u0=2φx

(6)

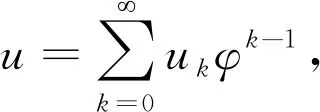
(7)

比较φ的同次幂系数，得

(8)

(9)

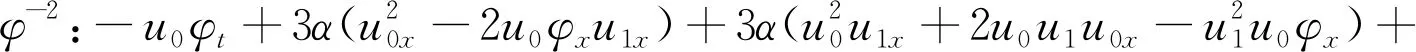
(10)

(11)

(12)

接下来计算调谐因子。对(7)移项得

(13)

设i=j+3，则式(13)变换为

(14)

式(14)中Fi为ui-1，uj-2，…u0，φ的函数。

1.1 分支Ⅰ的Painlevé分析和Bäcklund变换

当u0=φx时，由(14)式，计算调谐因子得i=-1，1，3。 若令u1=0，经过计算推出i≥2时，ui=vi=0，该方程具有Painlevé性质。

命题1Sharma -Tasso-Olever方程(1)有Bäcklund变换：

(15)

式中：φ满足方程(16)和(17)。

证明利用关系式(8)～(12)，将(5)代入得

φ-4：u0=φx；

φ-3：恒等式，可取u1=0；

φ-2：φt=-αφxxx

(16)

φ-1：φxt=-αφxxxx

(17)

(18)

对(16)等式两边对x求导，得

φtx=-αφxxxx

(19)

由式(17)和(19)联立，得相容条件：

φxt=φtx

由(18)易见u1满足方程(1)，即为方程的解，同时u为方程的解， 故(15)为方程(1)的Bäcklund变换。

1.2 分支Ⅱ的Painlevé分析和Bäcklund变换

当u0=2φx时，由(14)式，计算调谐因子得i=-2，-1，3。 若令u2=0，经过计算推出i≥2时，ui=vi=0，该方程具有Painlevé性质。

命题2Sharma -Tasso-Olever方程(1)有Bäcklund变换：

(20)

式中，φ满足方程(22)和(23)。

证明利用关系式(8)～(12)，将(6)代入得

φ-4：u0=2φx

(21)

(22)

(23)

(24)

由式(24)易见u1满足方程(1)，即为方程的解，同时u为方程的解。 故(20)为方程(1)的Bäcklund变换。

2 Sharma -Tasso-Olever方程的精确解

2.1 分支I的精确解

当u0=φx时，设方程(1)有指数形式的解：

φ(x，t)=ekx+ct+1

(25)

将式(25)代入式(16)，得

c=-αk3

取k=1，则c=-α，将k和c代入式(25)中，可以得到

φ(x，t)=ex-αt+1

(26)

将式(26)代入方程(1)的Bäcklund变换(15)中，可以得到

就是方程(1)的1个精确解。

2.2 分支Ⅱ的精确解

当u0=2φx时，设方程(1)有指数形式的解：

φ(x，t)=ekx+ct+1

(27)

将式(27)代入式(20)，得

(28)

其中：k和c为任意常数。(28)式是方程(1)的1个精确解。

3 结论

本文应用Painlevé 分析法，对Sharma-Tasso-Olever方程进行研究，证明了方程在满足一定约束条件的时候是Painlevé 可积的，得到了其自Bäcklund变换和精确解。将Painlevé 分析方法推广应用到其他的非线性偏微分方程有待进一步研究。