一类丢番图方程的全部正整数解

邓乃娟，袁平之

(1.湛江幼儿师范专科学校 数学系，广东 湛江，524000； 2.华南师范大学 数学科学学院，广东 广州，510631)

丢番图方程是数论的一个重要的分支，而指数型的丢番图方程又是其中较难的一个类型。到目前为止，指数型的丢番图方程仍是一个热门的研究课题，有很多的数论学者从事其研究，并且也得到了大量的研究结果。 比如： LJUNGGREN[1]得到了丢番图方程：

(1)

的全部正整数解。孙琦和袁平之[2]得到丢番图方程

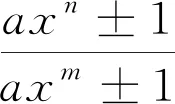
的全部正整数解。随后罗家贵[3-4]、曹珍富[5]和袁平之[6]分别得到了丢番图方程

的全部正整数解。2001年,袁平之和罗家贵[7]又得到了丢番图方程

的全部正整数解。在最近几年，数论工作者们又得到了一些指数型丢番图方程的一些正整数解，具体可见文献[ 8-14]。

本文主要运用二次丢番图方程的结论继续研究高次丢番图方程

的全部正整数解(a,x,y,m,n)，并且得到如下结论。

定理1不定方程

(2)

仅有平凡解a=cxn-2m,y=x(n-m)/2。

定理2不定方程

(3)

无正整数解。

在本文中要求a>0,x>1,y>0,n>m且a,x,y,m,n∈N。下面先介绍一些预备知识。

1 引理

引理1.1[4]设D是非完全平方正整数，(x0,y0)是Pell方程

x2-Dy2=±1

(4)

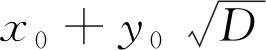
引理1.2[4]1) 设D是1个非完全平方正整数,则方程

x2-Dy2=1

(5)

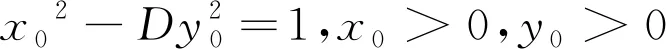
2)设D是1个正整数且非完全平方数,若方程

x2-Dy2=-1

(6)

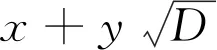
引理1.3[6]设方程

kx2-ly2=c,c=1,2,4.

当k>1或c=2时，该方程的所有正整数解(xn,yn)满足

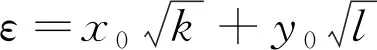
引理1.4[6]设D是非平方数且8或不整除D。

1)若2|D，则这些方程kx2-ly2=1,k>1,kl=D中有且只有一个方程有正整数解。

2)若2不整除D，则这些方程kx2-ly2=1,k>1,kl=D;kx2-ly2=2,k>0,kl=D中有且只有一个方程有正整数解。

3)若2不整除D和x2-Dy2=4有正整数解(x,y)，其中x,y为奇数，则这些不定方程kx2-ly2=4,k>1,kl=D中有且只有1个方程有正整数解。

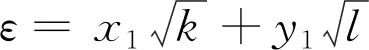
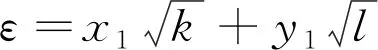
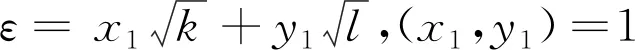
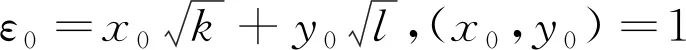
2 定理的证明

定理1的证明情形1：当c=1时，令axm=bu2,u>0,b>0无平方因子，于是，指数方程(axn-1)/(axm+1)=y2-1可变形成

bu2(xn-m+1)=(bu2+1)y2

(7)

由于(bu2,bu2+1)=1，因此，bu|y。不妨设y=buy1，代入(7)得

b(bu2+1)y12-xn-m=1

(8)

另一方面，方程

(bu2+1)X2-bY2=1

(9)

综上，(axn-1)/(axm+1)=y2-1仅有平凡解a=xn-2m,y=x(n-m)/2。

情形2：当c=2时，若2不整除axm，令axm=bu2,u>0,b>0无平方因子，于是，指数方程(axn-2)/(axm+2)=y2-1可变形成

bu2(xn-m+1)=(bu2+2)y2

(10)

由于(bu2,bu2+2)=1，因此，bu|y。不妨设y=buy1，代入(10)式得

b(bu2+2)y12-xn-m=1

(11)

另一方面，方程

(bu2+2)X2-bY2=2

(12)

若2|axm，令axm=2bu2,u>0,b>0无平方因子，于是，指数方程(axn-2)/(axm+2)=y2-1可变形成

bu2(xn-m+1)=(bu2+1)y2。

由c=1时的公式(7)，(8)和(9)的讨论知b=1，即axm=2u2。再由引理1.2知

从而，x与u同奇偶，故x(n-m)/2的所有素因子因子整除u。再由引理1.5得u=x(n-m)/2,y1=1，即a=2xn-2m,y=x(n-m)/2。

综上，(axn-2)/(axm+2)=y2-1仅有平凡解a=2xn-2m,y=x(n-m)/2。

情形3：当c=4时，若2不整除axm，令axm=bu2,u>0,b>0无平方因子，则指数方程(axn-4)/(axm+4)=y2-1可变形成

bu2(xn-m+1)=(bu2+4)y2

(13)

由于(bu2,bu2+4)=1，因此，bu|y。不妨设y=buy1，代入(13)式得

b(bu2+4)y12-xn-m=1

(14)

另一方面，方程

(bu2+4)X2-bY2=4

(15)

(bu2+4)X2-bY2=1

从而，axm=u2，即x(n-m)/2的所有素因子整除u(u2+3)/2。这时，结合引理2.5可得x(n-m)/2=u(u2+3)/2,y1=(u2+1)/2。这与u≡1(mod 2),y1≡0(mod 2)相矛盾。

若2‖axm，令axm=2bu2,u>0,b>0无平方因子且2不整除bu2，于是，指数方程(axn-4)/(axm+4)=y2-1可变形成

bu2(xn-m+1)=(bu2+2)y2。

由c=2时的公式(10)，(11)和(12)的讨论知(13)式无正整数解。

若4|axm，令axm=4bu2,u>0,b>0无平方因子，则指数方程(axn-4)/(axm+4)=y2-1可变形成

bu2(xn-m+1)=(bu2+1)y2。

由c=1时的公式(7)，(8)和(9)的讨论知b=1，即axm=4u2。再由引理1.2知

从而x与u同奇偶，故x(n-m)/2的所有素因子因子整除u。再由引理1.5得u=x(n-m)/2,y1=1，即a=4xn-2m,y=x(n-m)/2。

综上，(axn-4)/(axm+4)=y2-1仅有平凡解a=4xn-2m,y=x(n-m)/2。

定理2的证明情形1：当c=1时，令axm=bu2>1,u>0,b>0无平方因子，于是指数方程(axn+1)/(axm-1)=y2-1可变形成

bu2(xn-m+1)=(bu2-1)y2

(16)

由于(bu2,bu2-1)=1，因此，bu|y。不妨设y=buy1，代入(16)式得

b(bu2-1)y12-xn-m=1

(17)

另一方面，方程

bX2-(bu2-1)Y2=1

(18)

若b=1，则u2-1>1。将b=1代入(18)式得

(u2-1)y12-xn-m=1

(19)

而不定方程

(u+1)X2-(u-1)Y2=2

(20)

有整数解(X,Y)=(1,1)。若2不整除u2-1，则结合引理1.4知(19)式不成立。若2|(u2-1)，则2|(u-1),2|(u+1),4|(u2-1)，于是，方程

(21)

有正整数解(X,Y)=(1,1)，且(20)可变形为

(22)

故axm=u2=9,即(a,m,x)的可能取值为(1,2,3),(1,1,9),(3,1,3)。分别代入(18)式得3n-2+1=8y12,9n-1+1=8y12,3n-1+1=8y12,这均与n≡m(mod2)相矛盾。

若b>1，则由引理1.4、公式(17)和(18)式知bu2-1=1，即axm=bu2=2。将b=2,u=1代入(16)式知x≡1(mod2)，于是axm=2与x>1相矛盾。

综上，(axn+1)/(axm-1)=y2-1无正整数解。

情形2：当c=2时，若2不整除axm，令axm=bu2>2,u>0,b>0无平方因子，于是，指数方程(axn+2)/(axm-2)=y2-1可变形成

bu2(xn-m+1)=(bu2-2)y2

(23)

由于(bu2,bu2-2)=1，因此bu|y。不妨设y=buy1，代入(23)式得

b(bu2-2)y12-xn-m=1

(24)

另一方面，方程

bX2-(bu2-2)Y2=2

(25)

有正整数解(X,Y)=(1,1)。根据引理1.4、公式(24)、(25)和2不整除b(bu2-2)且b(bu2-2)>1知(24)式不成立。

若2|axm，令axm=2bu2,u>0,b>0无平方因子，于是，指数方程(axn+2)/(axm-2)=y2-1可变形成

bu2(xn-m+1)=(bu2-1)y2

(26)

由c=1时的公式(16)，(17)和(18)的讨论知bu2=9或bu2=2。

当bu2=9时，代入(25)式得9(xn-m+1)=8y2，于是，x≡1(mod2)。又axm=2bu2=18，故(a,m,x)=(2,2,3),(2,1,9),(6,1,3)。分别代入(26)式得9(3n-m+1)=8y2,9(9n-m+1)=8y2,9(3n-m+1)=8y2,这均与n≡m(mod2)相矛盾。

当bu2=2时，b=2,axm=4，即2|x。又由于(bu2,bu2-1)=1，故由(26)式知bu2|y2，不妨设y=buy1，于是(26)式可变形为

b(bu2-1)y2-xn-m=1

(27)

从而由(27)式得x≡1(mod2)。这与axm=4,x>1相矛盾。

综上，(axn+2)/(axm-2)=y2-1无正整数解。

情形3：当c=4时，若2不整除axm，令axm=bu2>4,u>0,b>0无平方因子，于是指数方程(axn+4)/(axm-4)=y2-1可变形成

bu2(xn-m+1)=(bu2-4)y2

(28)

由于(bu2,bu2-4)=1，因此，bu|y。不妨设y=buy1，代入(28)式得

b(bu2-4)y12-xn-m=1

(29)

另一方面，方程

bX2-(bu2-4)Y2=4

(30)

bX2-(bu2-4)Y2=1

(31)

有正整数解。

当b>1时，由引理1.4、公式(29)和(31)知bu2=5，即axm=5，故 (a,m,x)=(1,1,5)，将其代入(29)式得5n-m+1=5y12，这与5n-m+1≡2(mod4)相矛盾。

当b=1时，代入(29)式得(u2-4)y12-xn-m=1。又因为

(u+2)X2-(u-2)Y2=4

(32)

有正整数解(X,Y)=(1,1)，故由引理1.6知方程 (u+2)X2-(u-2)Y2=1有正整数解。这时再结合引理1.4可得u2-4=u+2，即u=3,axm=9。从而(a,m,x)=(1,2,3),(1,1,9),(3,1,3)，分别代入(u2-4)y12-xn-m=1中得3n-m+1=5y12,9n-m+1=5y12,3n-m+1=5y12，这与3n-m+1≡9n-m+1≡2(mod4)相矛盾。

若2||axm，令axm=2bu2>4,u>0,b>0无平方因子且2不整除bu2，于是，指数方程(axn+4)/(axm-4)=y2-1可变形成

bu2(xn-m+1)=(bu2-2)y2

(33)

当c=2时，由公式(23)，(24)和(25)的讨论知(32)式无正整数解。

若4|axm，令axm=4bu2,u>0,b>0无平方因子，于是，指数方程(axn+4)/(axm-4)=y2-1可变形成

bu2(xn-m+1)=(bu2-1)y2

(34)

由c=1时的公式(16)，(17)和(18)的讨论知bu2=9或bu2=2。

当bu2=9时，代入(34)式得9(xn-m+1)=8y2，于是，x≡1(mod 2)。又axm=4bu2=36，故(a,m,x)=(4,2,3),(4,1,9),(12,1,3)。分别代入(34)式得9(3n-m+1)=8y2,9(9n-m+1)=8y2,9(3n-m+1)=8y2,这均与n≡m(mod 2)相矛盾。

当bu2=2时，b=2,axm=8，即2|x。又由于(bu2,bu2-1)=1，故由(34)式知bu2|y2，不妨设y=buy1，于是，(34)式可变形为

b(bu2-1)y2-xn-m=1

(35)

从而由(35)式得x≡1(mod2)。这与axm=8,x>1相矛盾。

综上，(axn+4)/(axm-4)=y2-1无正整数解。