单诱骗态量子数字签名协议性能分析

王东, 张华, 燕飞, 张畇涵,宋萧天, 赵义博∗

(1 云南天衢量子科技有限公司, 云南 昆明 650000;2 中国科学院电子学研究所,微波成像技术国家重点实验室, 北京 100190)

1 引 言

数字签名于1976 年由Diffie 和Hellman 提出[1],广泛应用于诸多方面,如远程通信、电子邮件、金融交易等,是现代密码学最基础和实用的发明之一[2]。数字签名通常用于保证信息被合法用户在身份得到认证的条件下进行签名,同时确保信息可转移、不可伪造、不可抵赖。然而,目前常用的数字签名协议都是采用公钥体制,其安全性依赖于特定问题的计算复杂度假设,例如RSA[3]、DSA[4]、EDSA[5]。随着量子计算机的出现,经典数字签名的安全性面临着严峻的考验。幸运的是,2001年提出的量子数字签名(Quantum digital signature,QDS)协议提供了基于量子力学原理的信息论安全性。原始的量子数字签名协议[6]要求长时间的量子存储、非破坏性的量子态比较技术以及安全的量子信道,因此实现技术难度大,不具备实用性。

为了提高量子数字签名的实用性,研究者相继提出了各种改进协议[7～10]。其中,Amiri 等[10]提出的量子数字签名协议不再需要安全的量子信道假设,在相干攻击下仍可实现无条件安全性,并且可直接利用现有的量子密钥分发(Quantum key distribution,QKD)[11～13]系统来实现,大大提高了量子数字签名的实用性。该协议[10]采用了与QKD 相同的密钥生成协议(Key generation protocol,KGP)来生成初始密钥,但是无需进行纠错和保密放大等后处理过程。在这种QDS 协议中,除KGP 阶段为量子过程外,其余阶段的通信均为经典过程。近年来,随着各种实验工作的开展[14～23],量子数字签名也逐渐走向实用化。目前,QDS 已经在差分相位协议[17,18]、BB84 协议[19～21]、测量设备无关协议[22,23]等QKD 系统上得到了实验验证。例如,文献[20]基于稳定的GHz Faraday-Sagnac-Michelson BB84 QKD 系统,实现了25 dB 信道损耗下0.044 bit/s 的量子签名,具有较高的实用性。文献[21]实现了目前最远距离的量子签名,达到了280 km。

QDS 协议的效率可以用签名率来评估,即单位时间内签名的比特数。在给定的安全参数下,应尽可能减少签名一个比特所需的KGP 过程产生的密钥比特数,以提升系统的签名率。确定系统签名一个比特所需的最小块长,一般需要借助于诱骗态方法来进行参数估计[24]。诱骗态方法[25～27]的提出是为了在QKD 协议中使用弱相干光源替代目前无法实现的理想单光子源,以抵御窃听者针对光源存在多光子项的漏洞所进行的光子数分离(Photon number splitting,PNS)攻击[28]。诱骗态方法的提出大大提高了系统的安全性和实用性,该方法同样适用于QDS 协议。2 诱骗态QDS 协议[10]在密钥有限长条件下的安全性已得到证明,且得到了实验验证[20]。然而在实际情况下,由于统计涨落和光强调制误差的存在,增加诱骗态个数并不一定总能得到有益的效果。事实上,单诱骗态QKD 协议[29]的性能已被证明在多数情况下比2 诱骗态协议效果更好,并且实现起来更加简单。为进一步提升QDS 系统的签名率,将单诱骗态方法应用于QDS 系统中,本文提出了一种基于单诱骗态的QDS 协议,按照文献[10]的方法对该协议的安全性进行分析。数值模拟结果表明,在相同的系统参数下,单诱骗态协议的表现优于2 诱骗态协议。

2 单诱骗态量子数字签名协议及其安全性分析

考虑三方之间的量子数字签名协议,即发送者Alice 将一个消息结合数字签名发送给两个接收者Bob 和Charlie, 并且假设最多只有一方是不诚实的。根据文献[10], 量子数字签名协议共分为两个阶段:分发阶段和消息阶段。在分发阶段,Alice 分别与Bob 和Charlie 进行独立的KGP 过程,分别产生关联的密钥串。具体地,由Bob 和Charlie 分别独立地向Alice 发送量子态,Alice 对接收到的量子态进行测量。在消息阶段,Alice 作为发送者,向Bob 和Charlie 进行经典的消息发送和签名。下面详细介绍单诱骗态量子数字签名协议的过程。

分发阶段：

1)对于每一个待签名的经典比特m(m=0/1),Bob(或Charlie)随机将4 种BB84 态(Z 基和X 基)制备到NB(NC)个相干态脉冲上,并通过强度调制器制备信号态(平均光子数u1)和诱骗态(平均光子数u2)脉冲,然后通过不安全的量子信道发送给Alice。Alice 随机选择X 基或Z 基对接收到的光子进行测量。

2)Bob(或Charlie)和Alice 通过经典信道进行对基操作,同时公布诱骗态信息。他们保留基一致的结果,生成长度为(1+k)L 的筛后密钥。

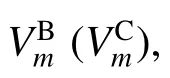
消息阶段:

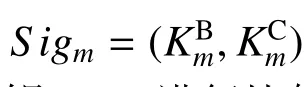
3)Bob 将这条签名消息(m,S igm)转发给Charlie。

需要注意的是,在分发阶段,Bob 和Charlie 可以分别独立地向Alice 发送量子态,即二者分别与Alice独立地完成KGP 过程。考虑有限长效应,按照文献[10]的方法来分析单诱骗态QDS 协议的安全性。

令pE为攻击者在KGP 过程引入的最小误码率,满足

式中NW,µ为W 基下强度为µ的脉冲计数n(错误计数m),NW为W 基下的总脉冲计数,εPE为有限长效应下参数估计的失败概率,τn=∑µpµe−µµn/n!,nX= L/2。

系统的诚实放弃概率P(Honest abort)为当三方都诚实,由于误码的存在而放弃整个签名过程的概率,满足条件[18]

抵赖概率P(Repudiation)表示Alice 对一条信息签名并成功抵赖的概率,可表示为

式中sa和sv满足

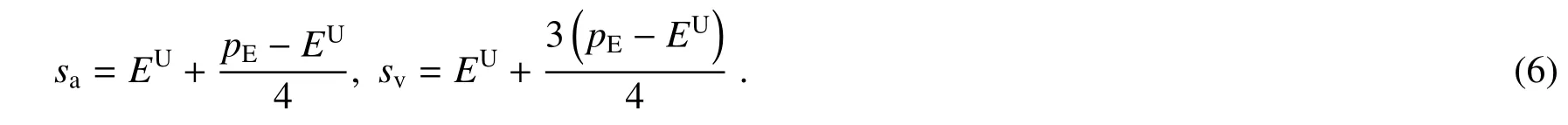
P(Forge)为Bob 或Charlie 伪造Alice 签名成功的概率,可表示为

此时诚实放弃概率、抵赖概率和伪造概率相同,即

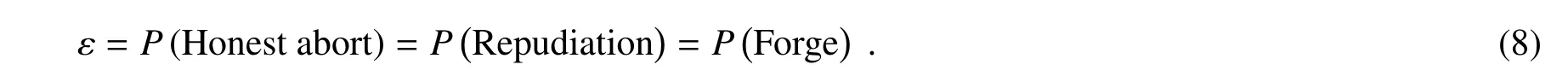
因此,协议的安全水平为ε,即签名没有被诚实放弃、抵赖以及伪造的概率为1 −ε。

3 数值模拟与讨论

假设Bob 和Charlie 的实验装置参数相同,发送的信号态和诱骗态脉冲的平均光子数分别为µ=u1、u2,相应的发送概率分别为pu1、1 −pu1,选择X 基和Z 基的概率分别为pX和1 −pX。考虑信道损耗为LC,Alice 端损耗为LA,探测器的平均探测效率、暗计数概率和后脉冲概率分别为ηd、Pd、Pap,那么对于强度为µ的脉冲,探测器的探测概率和相应的错误概率分别为

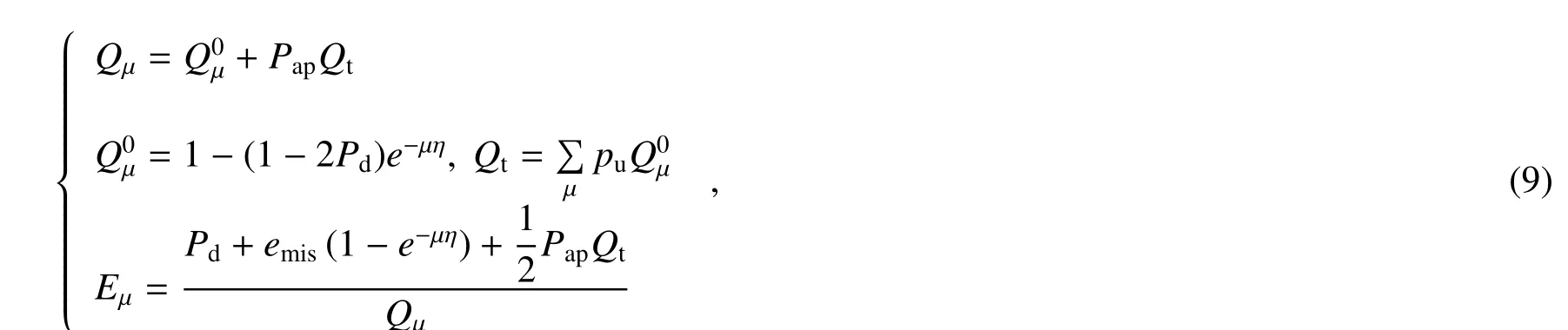
式中emis为系统的光学本底误码,η = ηd10−0.1(LA+LC),Q0µ为不考虑后脉冲影响[30,31]时强度为µ的脉冲响应率,Qt为不考虑后脉冲影响时信号态和诱骗态脉冲的总响应率,Eµ为考虑后脉冲影响时强度为µ的脉冲误码率。

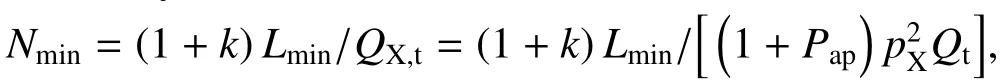
由(9)、(10)式可以看出签名率是参数Lmin、u1、u2、pu1、pX的函数S (Lmin,u1,u2,pu1,pX)。为了得到各距离下的最高签名率,需要对参数u1、u2、pu1、pX以及Lmin进行优化。

而由(4)、(6)式可得

将(11)式代入(1)式中,可以得到约束条件

当给定实验参数, 并固定协议安全参数ε 时, 根据约束条件(12) 以及各参数的取值范围即可对S (Lmin,u1,u2,pu1,pX)在不同传输距离下的签名率进行最优化。需要说明的是,密钥块长Lmin是在满足约束条件(12)的情况下,使系统签名率达到最大的最优值,而不是固定值,发送的总脉冲个数也不是固定的,这与QKD 中安全成码率的最优化过程不同。

Table 1 Parameters used in the simulation

采用文献[20]中的实验参数来对系统的签名率进行数值模拟,用到的参数设置如Table 1 所示。首先,假设信道采用标准通信光纤,衰减系数为0.2 dB/km,则距离为l 的信道损耗为LC= 0.2l。Alice 端的损耗假设为6 dB。选取参数估计的失败概率设置为εPE=10−10,固定协议安全参数ε=10−10。采用相同的实验参数,通过数值模拟进行参数优化,可对所提出单诱骗态QDS 协议和2 诱骗态协议进行比较。

Fig.1 给出了单诱骗态协议(S1)和2 诱骗态协议(S2)的签名率随距离变化的仿真曲线。为了能够更直观地体现单诱骗态协议的性能提升,给出了两种协议在不同距离下的签名率比值。可以看出,在传输距离为140 km 以内,单诱骗态协议的签名率较2 诱骗态协议有一定的提升;而在超过140 km 的情况下,单诱骗态协议的签名率下降较快,最远传输距离比2 诱骗态协议少10 km 左右。在QKD 系统中,对安全成码率进行最优化时常规的做法是固定后处理密钥块长,得到的结果是短距离内2 诱骗态协议比单诱骗态协议更有优势。然而在对QDS 系统的签名率进行最优化时,固定的是安全参数而不是后处理密钥块长,导致单诱骗态协议在距离140 km 以内一直比2 诱骗态协议具有优势,这是导致二者趋势不同的主要原因。

Fig.2 给出了不同传输距离下,能够安全签名半个比特所需要的最少密钥长度(n 为Bob 保留的密钥长度)。可以看出,在120 km 以内,单诱骗态方法所需要的密钥比特数少于2 诱骗态方法。当距离超过120 km 之后,单诱骗态方法所需的密钥比特数上升趋势明显高于2 诱骗态方法,这也符合Fig.1 中单诱骗态方法与2 诱骗态方法的签名率比值在120 km 之后快速下降的趋势。

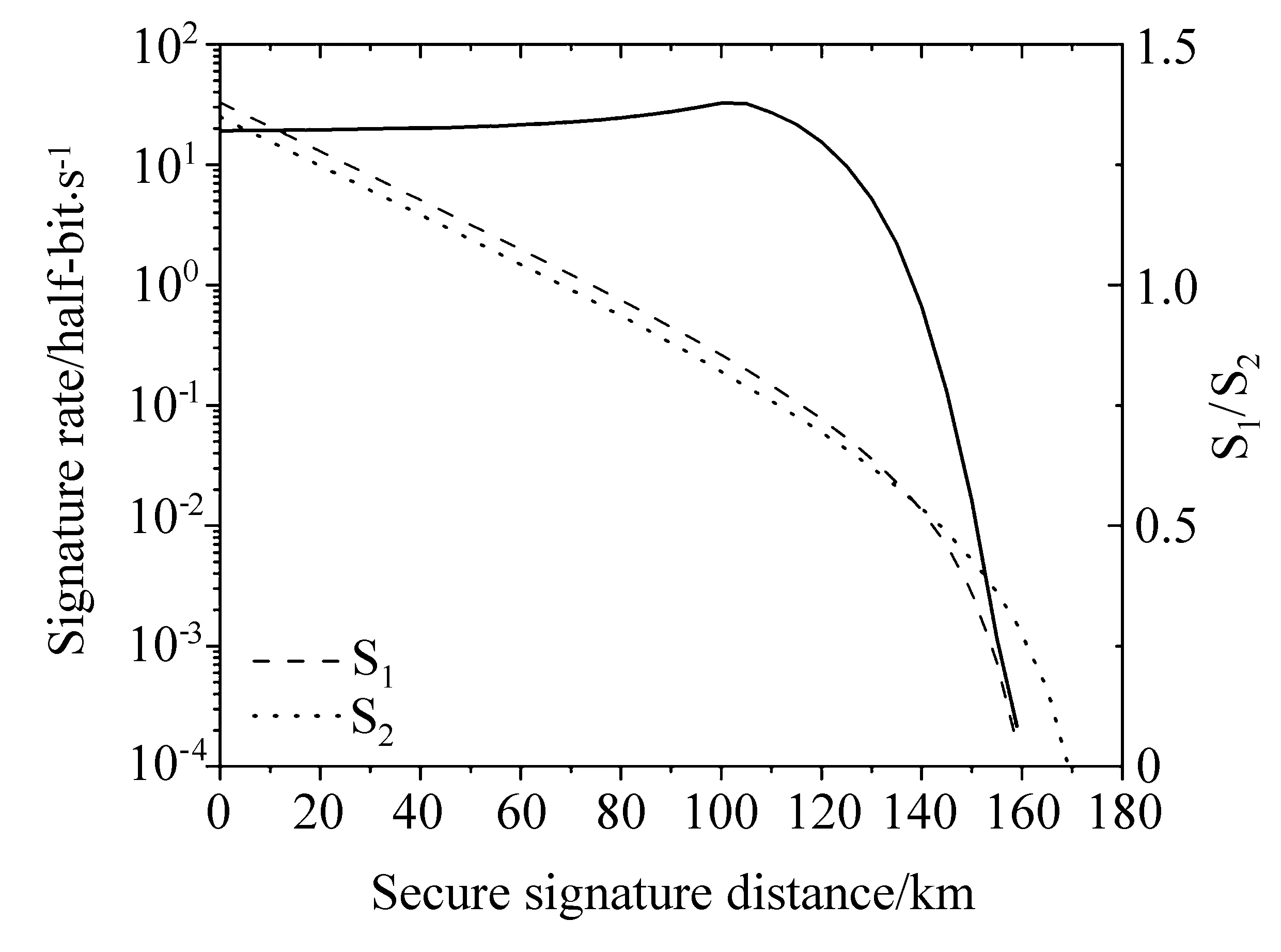
Fig.1 Simulation results of signature rate with 1-decoy state method(S1)and 2-decoy state method(S2)by parameters optimization,and the ratio of S1 to S2

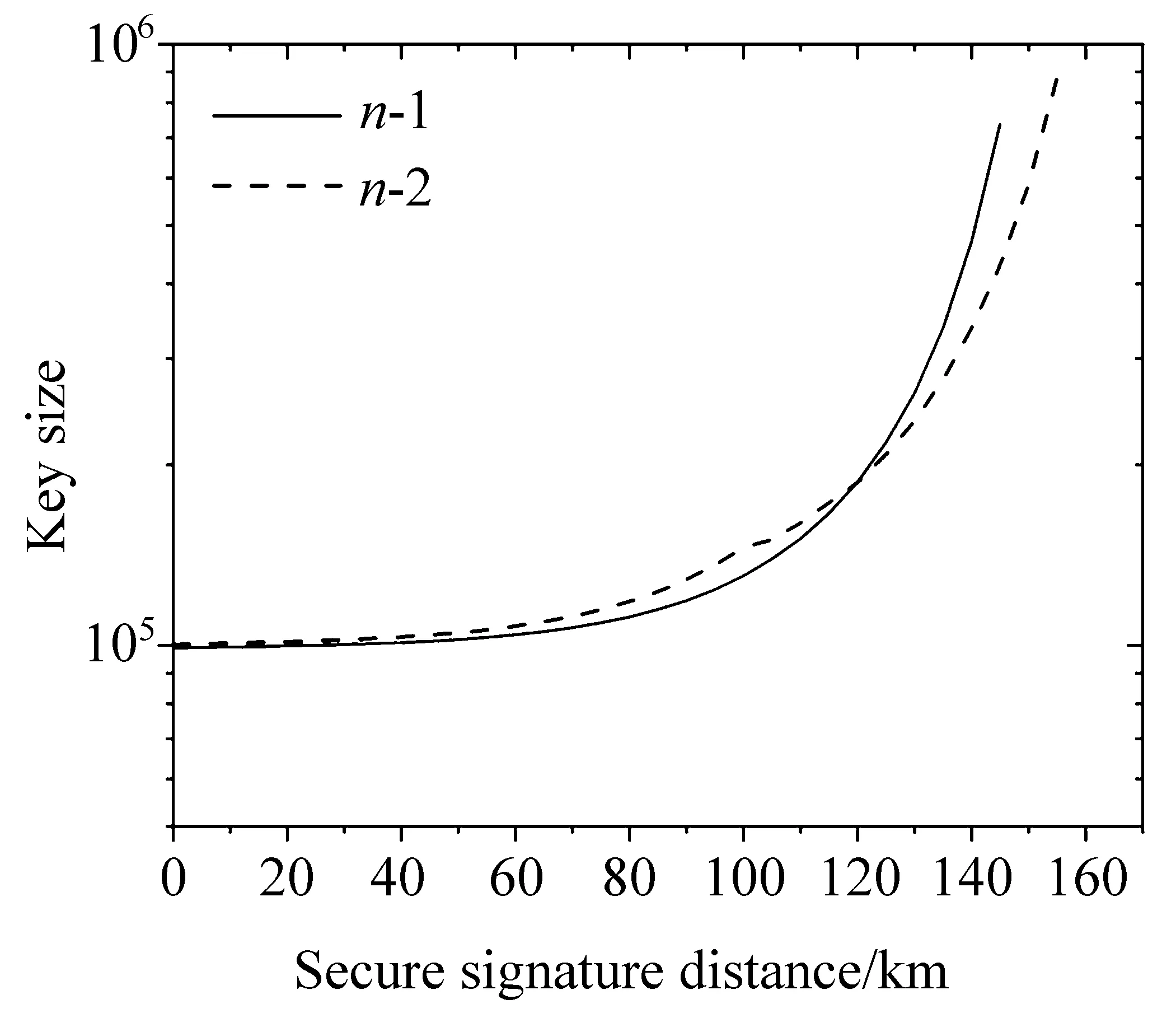
Fig.2 Minimum key bits that Bob required to keep in the distribution stage when signing a half-bit,with n −1 for the 1-decoy state method and n −2 for the 2-decoy state method

4 结 论

提出了一种单诱骗态量子数字签名协议,并给出了简单的安全性证明。通过数值模拟并进行参数优化,比较了单诱骗态协议和2 诱骗态协议在不同传输距离下的签名率。数值模拟结果表明,单诱骗态协议的签名率比2 诱骗态协议在大多数距离下略有提升,在距离120 km 以内的优势较为平稳。虽然在签名率方面单诱骗态协议与2 诱骗态协议相比优势不够明显,但单诱骗态协议的量子态调制更加简单、易于实现,可以降低系统的复杂度和光强调制误差对系统性能的影响。因此,总体看来,单诱骗态协议具有更好的性能和实用性。