基于腔QED制备三原子W纠缠态

张 蕾, 郝丹辉, 强稳朝

(1 西安建筑科技大学华清学院, 陕西 西安 710043;2 西安建筑科技大学理学院, 陕西 西安 710055)

1 引 言

量子纠缠是一种重要的量子力学现象,作为量子信息科学中的基本资源,有其重要的应用。例如:量子通信[1]、量子密钥[2]、量子隐形传送[3]、量子稠密编码[4]等。常见的量子纠缠态有:EPR 态[5]、GHZ态[6]和W 态[7]、Cluster 簇态[8]等,然而多粒子纠缠态与两粒子纠缠态相比有更强的量子非局域关联,在量子信息处理中更具优势。在三量子体系中,研究最多的两类纠缠态是GHZ 态和W 态,两者之间不能通过局域操作和经典通信(LOCC)相互转换。两者相比,W 态携带信息更稳定,在量子比特丢失方面抵抗性强,而且在量子网络匿名传输和最优量子普适克隆机[9]构建中扮演着重要角色。可见,W 纠缠态的制备及其应用的研究具有非常重要的学术意义和实用价值。近几年,人们研究了很多种关于纠缠态制备的方法,主要有: 核磁共振、腔QED[10]、离子阱[11]、超导量子干涉仪[12]等。还有较多研究是基于腔QED 通过原子与腔共振相互作用制备W 纠缠态的[13～17],在此类W 纠缠态制备过程中最主要的障碍就是腔场的消相干(耗散),同时对腔的品质要求很高。还有较多研究是基于腔QED,通过原子与腔大失谐(非共振)相互作用来制备W 纠缠态[18～20],采用大失谐相互作用的优点是: 有效克服了光腔的消相干,腔的耗散和热辐射对系统影响小,对腔的Q 值要求不高,并且针对腔QED 双光子过程比单光子过程更有优势[21],使得方案更易于在实验中实现。

以上研究都是利用一个原子与三或四个腔场相互作用,本文提出一个基于腔QED,并利用三个全同三能级原子与一个腔场非共振相互作用制备三原子W 纠缠态的方案。该方案中,最初三个原子分别处于激发态和基态,腔场处于真空态,三个原子先后被送入该腔场,选择合适的原子与腔场之间的相互作用时间就可获得W 纠缠态。进而讨论了该方案的实验可行性,研究还发现在耦合常数不同的情况下,失谐量对保真度的影响程度不同。

2 理论模型及数值计算

要构建的W 纠缠态为

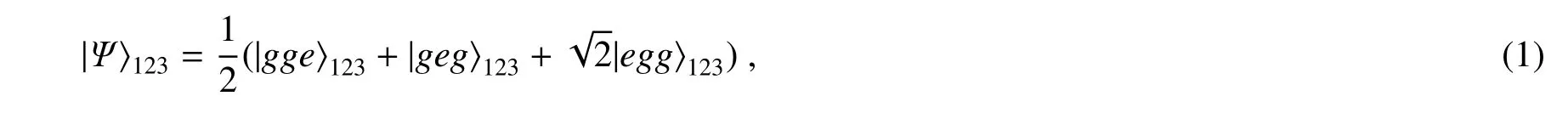
式中1、2、3 表示三个原子。在Jaynes-Cummings 模型中,通过双光子过程,描述一个三能级原子与单模腔场作用,在旋波近似下,相互作用绘景中,有效哈密顿量可表示为[18,22]

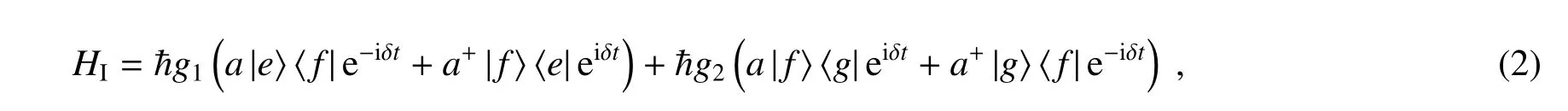
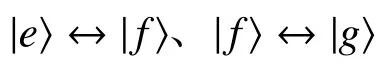
Fig.1 给出了三能级原子与单模腔场作用的原理图。其中Ω 是腔场频率,ωe、ωf、ωg分别是对应于原子能级|e〉、|f〉、|g〉的频率,则整个系统的态随时间的演化可表示为

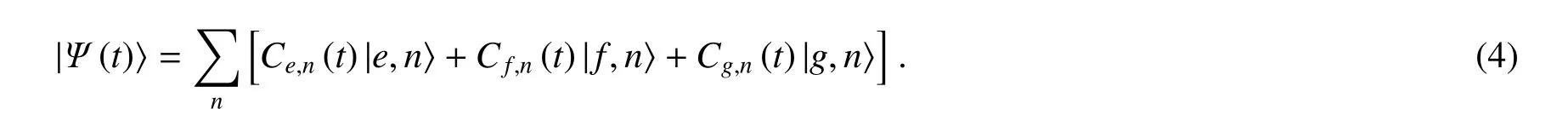
由薛定谔方程以及(2)式、(4)式,可得到微分方程

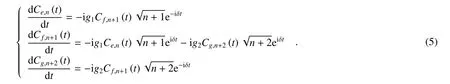
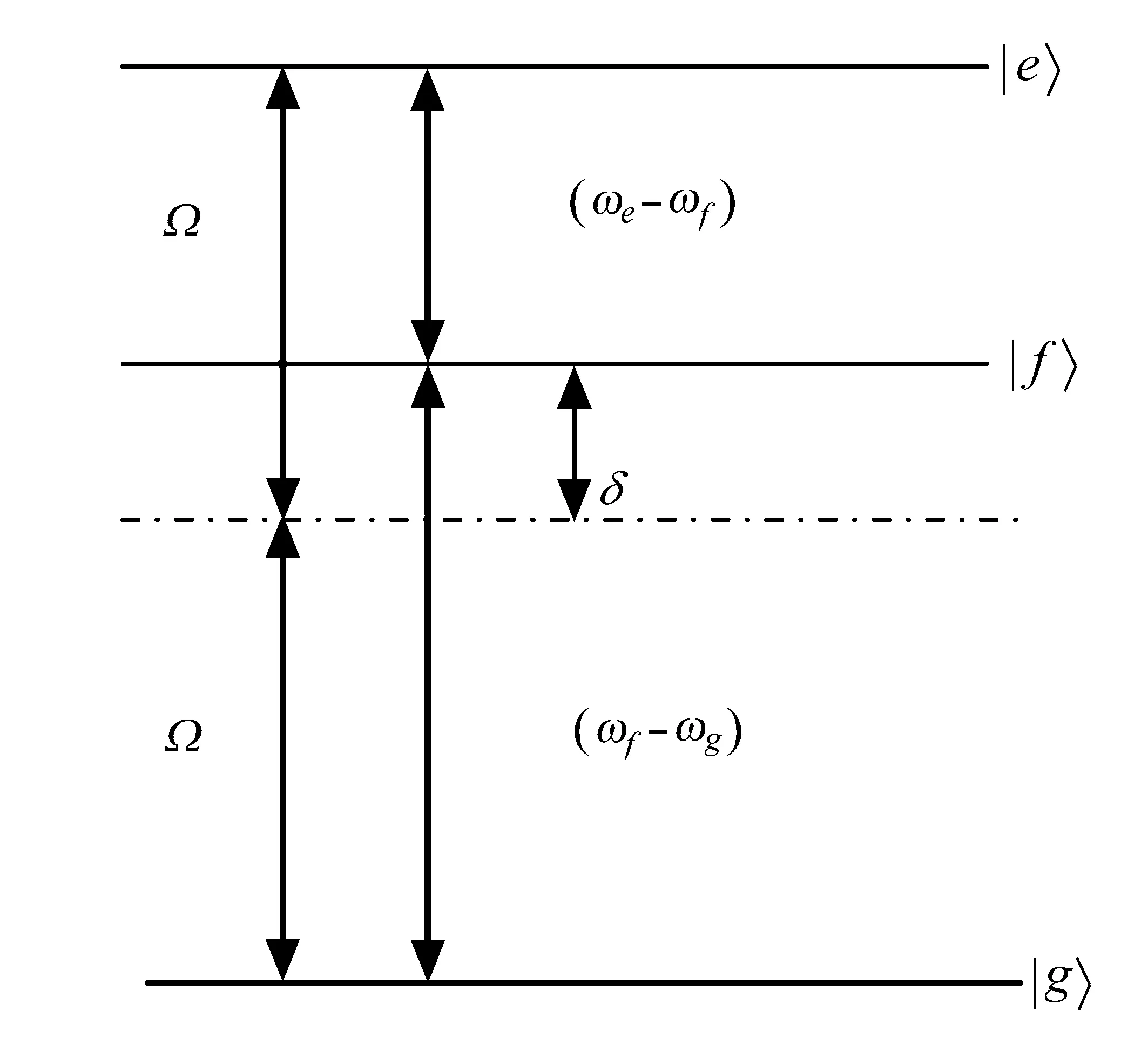
Fig.1 Schematic of three-level atom interacting with a single-mode cavity field

假定原子与腔场的初始态(初始时间t=0)为

式中Cn(0)表示初始场态的振幅,Ca(0)(a = e, f,g)为初始原子态(归一化)|χ〉 =Ce|e〉+Cf|f〉+Cg|g〉的振幅。根据这些初始条件,解薛定谔方程,可得到系数

假定与腔场作用的第一个原子1 和第二个原子2 均处在激发态,原子3 处在基态,腔场最初处在真空态。首先,将第一个原子1 注入腔中,与腔场作用时间t1,则系统的态将演化为

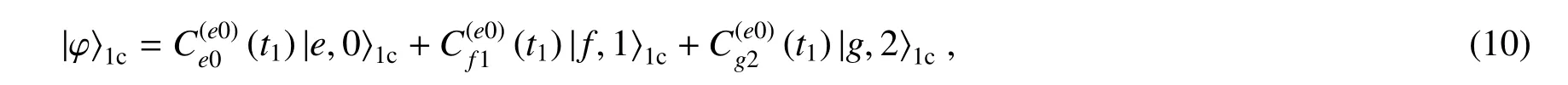
式中C(u,v)x,y表示(7)～(9)式中的系数,考虑到系统最初态处在(u, v), x、u 代表原子所处态,y、v 代表腔场所处态。

随后将第二个原子2 注入腔中,作用时间为t2后离开;再将第三个原子注入腔中,并与腔作用t3时间后,系统态可演化为

若探测腔场处于双光子态|2〉,此时系统将塌缩为

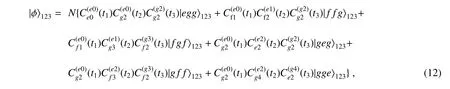
其成功概率为

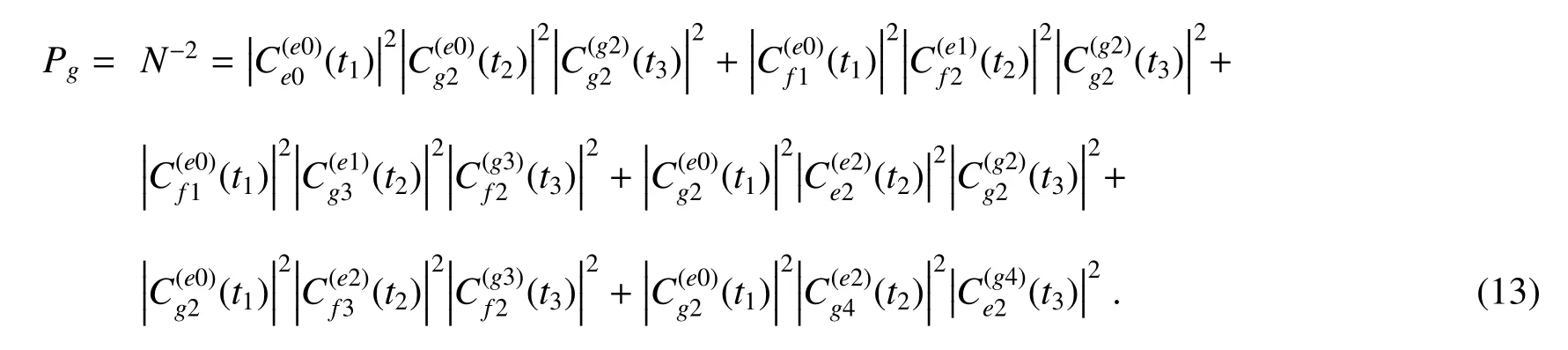
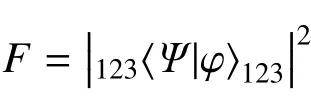
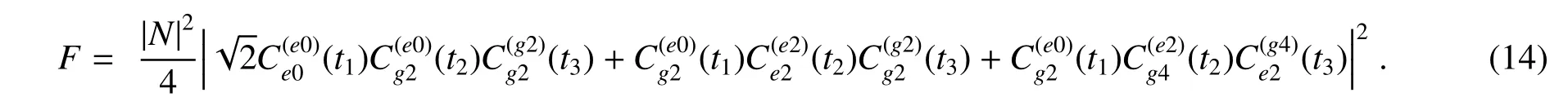
另外,该方案还可推广至制备任意分权重的W 态。假设该W 态的形式为

则通过该方案可获得的对应的保真度为

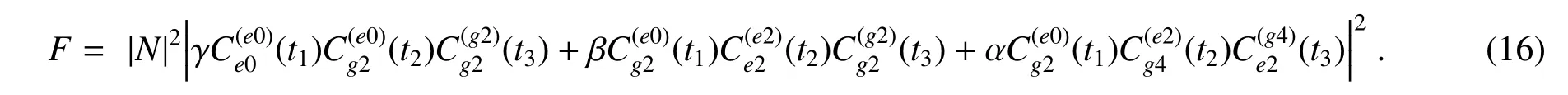
3 数值分析及讨论

当实验参数g1= g2= g = 17.5 MHz,失谐量δ = 9.95g,选择的是主量子数为n ～90 的里德堡原子,原子与腔场相互作用时间t1=4µs,t2=70.38µs,t3=78.25µs,可得到该态的保真度为98.0%、相应的成功概率为51.7%,如Table 1 所示。当实验参数g1= g2= g= 17.5 MHz,失谐量δ= 30g,原子与腔场相互作用时间t1= 1µs,t2= 40.8µs,t3= 21.4µs,可得到该态的保真度为99.3%、相应成功概率为57.7%,如Table 2 所示。Fig.2 更加直观与形象地反映了保真度随腔场与原子相互作用时间的变化关系。Fig.2(a)表示当g = 17.5 MHz、δ = 9.95g、t1= 4µs 时,其保真度随t2、t3的变化曲线;Fig.2(b)表示当g = 17.5 MHz、δ = 30g、t1= 1µs 时,其保真度随t2、t3的变化曲线。在制备三原子W 态的过程中,只需要在第三个原子离开腔之前保持腔场的相干性。整个过程所需的时间约为10−4s,远小于腔场的有效衰减时间。因此,在当前的实验条件下可实现该方案。

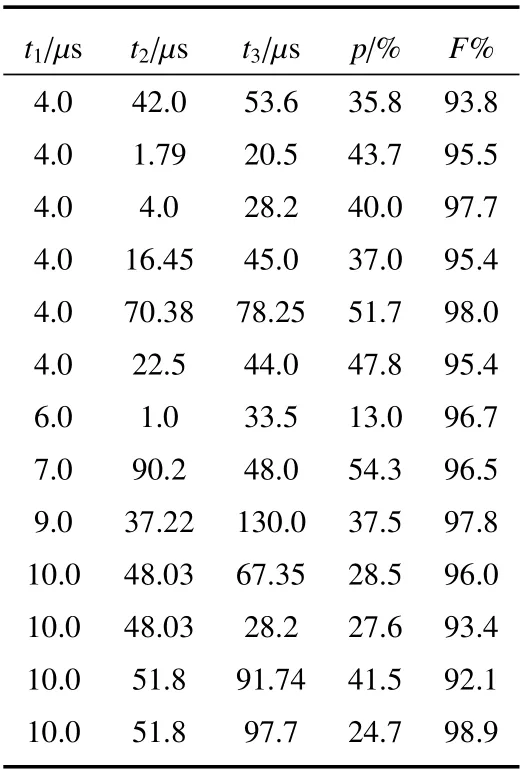
Table 1 Fidelity and corresponding success probability under different t1, t2 and t3 with g=17.5 MHz and δ=9.95g

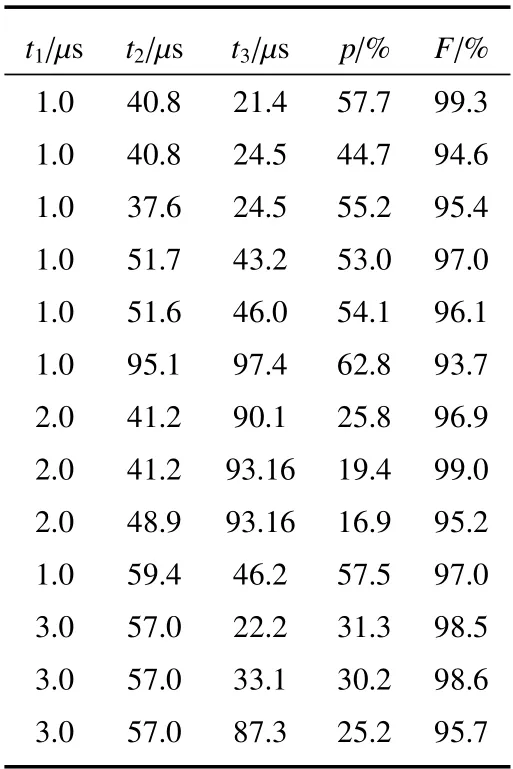
Table 2 Fidelity and corresponding success probability under different t1, t2 and t3 with g=17.5 MHz and δ=30g

当耦合常数g=1 MHz,原子与腔场作用时间为t1=6µs、t2=19.7µs、t3=4.2µs 时,保真度随着δ的增大出现了不规则的振荡,如Fig.3(a)所示,并且振荡的周期在逐渐增大,但整体趋势上保真度随着δ的增大在减小;当耦合常数g=17.5 MHz,原子与腔场作用时间为t1=4µs、t2=40.95µs、t3=54.75µs时,如Fig.3(b)所示,保真度随δ 的变化也出现了振荡,随着δ 的增大,振荡的周期变化不是很明显,振荡的幅度与Fig.3(a)相比整体上较为稳定。可见,耦合常数的不同使得失谐量对保真度的影响程度不同,但当失谐量δ=0 时,Fig.3(a)和Fig.3(b)中对应的保真度都为最大。

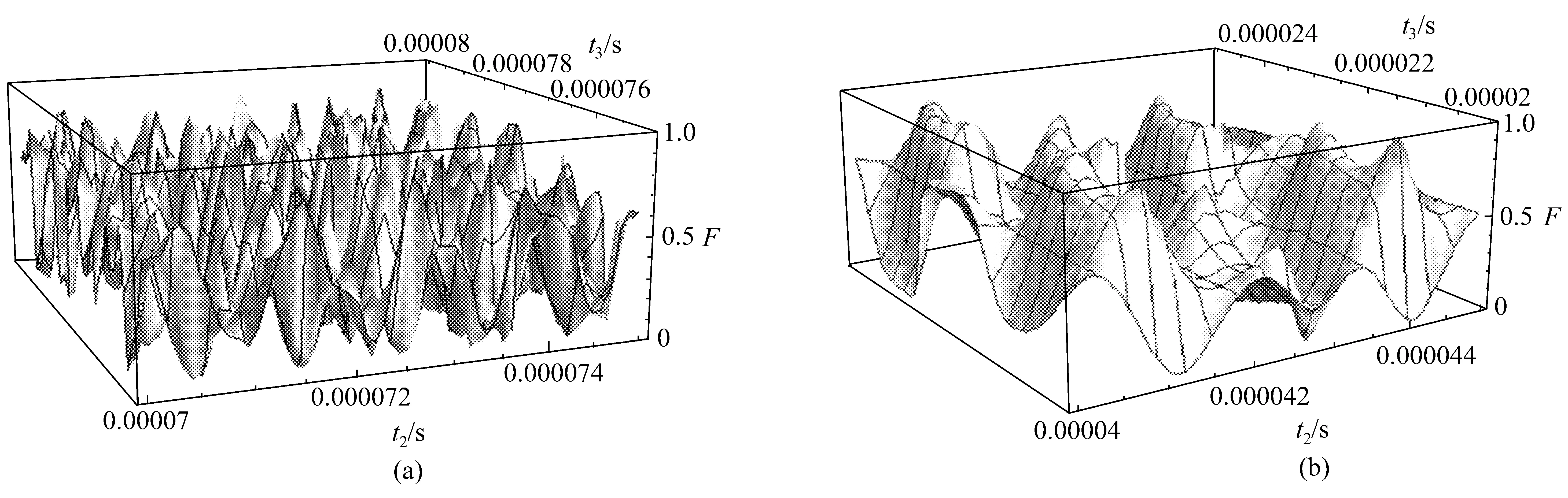
Fig.2 Fidelity versus t2,t3 for a fixed interaction time t1.(a)g=17.5 MHz,δ=9.95g,t1 =4µs;(b)g=17.5 MHz,δ=30g,t1 =1µs

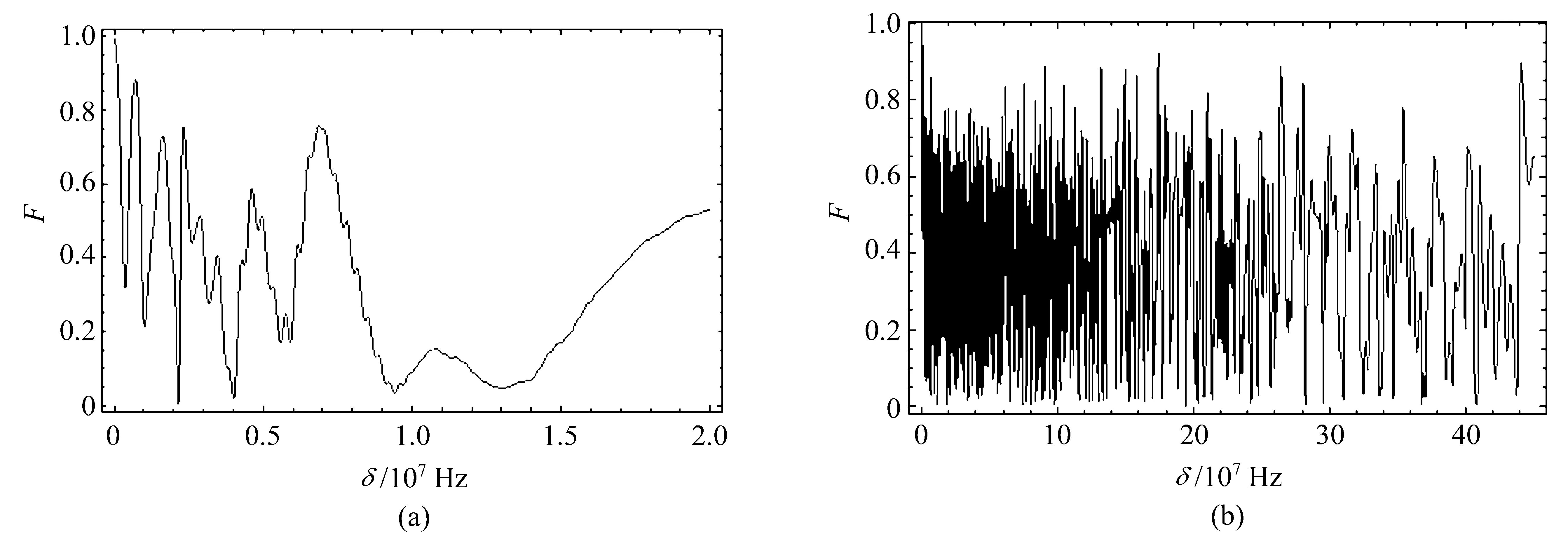
Fig.3 Fidelity versus the detuning δ. (a)g=1 MHz,t1 =6µs,t2 =19.7µs,t3 =4.2µs;(b)g=17.5 MHz,t1 =4µs,t2 =40.95µs,t3 =54.75µs

4 结 论

基于腔QED 提出了一种通过双光子过程、利用三个全同Ξ 型三能级原子与一个单模腔场非共振相互作用制备出具有最大保真度W 纠缠态的方案,分析和讨论了该方案的实验可行性以及失谐量对其保真度的影响,结果表明:1)当原子与腔场之间相互作用时间不同时,获得W 纠缠态的保真度以及相应的成功几率不同,通过合适选择相互作用时间可得到具有最大保真度的纠缠态,并且整个过程所需的时间10−4s 远小于腔场的衰减时间,因此,在当前的实验条件下该方案可实现;2)在耦合常数不同的情况下,保真度随着δ 的增大均出现了不同程度的振荡,可见,耦合常数的不同使得失谐量对保真度的影响程度不同。另外,根据该方案可以将其推广至制备任意分权重的W 态。