水力裂缝动态扩展的压裂液滤失模型

2020-12-11穆景福

石油地质与工程 2020年6期

罗攀，王崟，黄昊，孙晓，穆景福

（1.陕西延长石油（集团）有限责任公司研究院，陕西西安710075；2.陕西省页岩气勘探开发工程技术研究中心，陕西西安710075；3.中国石油长庆油田分公司采油十一厂，甘肃庆阳 745000）

水力裂缝作为压裂液滤失模型的边界，决定了滤失区域的大小，对滤失量具有重要影响。压裂过程中，水力裂缝长度逐渐增加，滤失区域逐渐变大，滤失量也会逐渐增加，而通常的滤失模型计算时采取了裂缝最终达到的固定长度，滤失速度开始时最大，然后递减，显然，这是违背物理事实的。经典滤失理论认为滤失是一维的，并且水力裂缝边界的长度不变，但实际滤失应该是二维甚至三维的，特别是当渗透率较高时，滤失空间的多维性更加明显，裂缝边界长度对滤失的影响很大。由任书泉、古法刚[1]提出的滤失模型考虑了侵入区前沿移动等多种因素，比经典滤失理论考虑的更多，更接近实际，但同样并未考虑滤失的多维性以及裂缝长度的变化；任岚[2]等提出了考虑压裂液平面流动的二维滤失模型，并以差分法求得数值解，更加适合高渗地层中压裂液滤失速度随时间变化的动态预测，但也没有给出裂缝长度变化对滤失速度的影响；李勇明[3]等在考虑裂缝性地层的滤失时，建立了双重介质模型，并以正交变换求解，但同样也未考虑滤失的多维性与裂缝边界的动态扩展；游先勇[4]等研究了天然裂缝成簇分布的滤失规律；夏富国[5-7]等考虑天然裂缝对滤失的影响。总之，现有研究多考虑裂缝在空间的变化，但很少考虑裂缝在时间上的变化。裂缝动态扩展使滤失问题变得很复杂，但却是不容忽略的条件，考虑后可以使现实问题得到更清晰更准确地认识。本文根据有限差分法实现了考虑裂缝动态扩展的二维压裂液滤失模型的求解，研究了裂缝动态扩展对滤失的影响，证实了裂缝长度的变化对滤失有着重要影响。

1 滤失模型

考虑压裂液的二维滤失和裂缝动态扩展，在矩形区域上建立二维滤失的偏微分方程。

式中：p 为地层压力，Pa；x、y 分别为研究区域的长度和宽度，m；η 为导压系数，m2/s；t 为滤失时间，s。

考虑到裂缝两侧的滤失情形具有对称性，取1/4 区域进行研究，每条边界具有不同的边界条件（图1）。

图1 网格节点和边界条件示意图

左侧边界为对称边界，即该边界上压裂液沿 x方向的滤失速度为0，其边界条件为：

式中： pi1，为第一列节点的压力值，Pa； pi2，为第二列节点的压力值，Pa；i 为x 方向上的网格节点编号。

右侧边界和上侧边界均为定压边界，为原始油藏压力，其边界条件为：

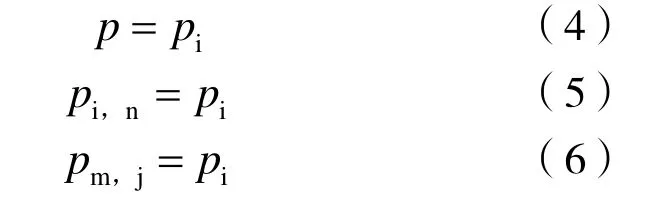
式中： pi为原始油藏压力，Pa； pi,n为最右一列网格节点的压力值，Pa； pm，j为最上一行网格节点的压力值，Pa； j 为y 方向上的网格节点编号。

下侧边界的条件较为复杂，其中，水力裂缝长度的公式为：

式中：L 为水力裂缝长度，m；vel 为裂缝扩展速度，m/s； tv为裂缝扩展时间，s。

0 < x ≤L 的部分边界对应水力裂缝，该部分边界取定压边界条件：

式中： pf为裂缝内压力，Pa。

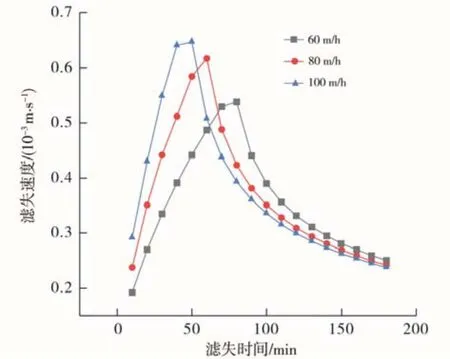
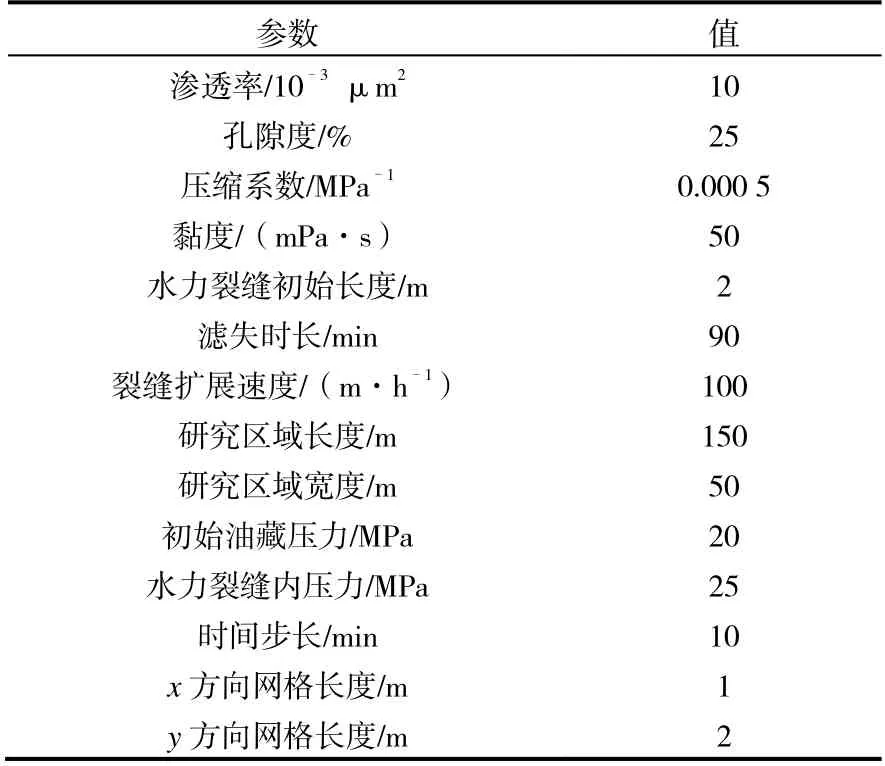
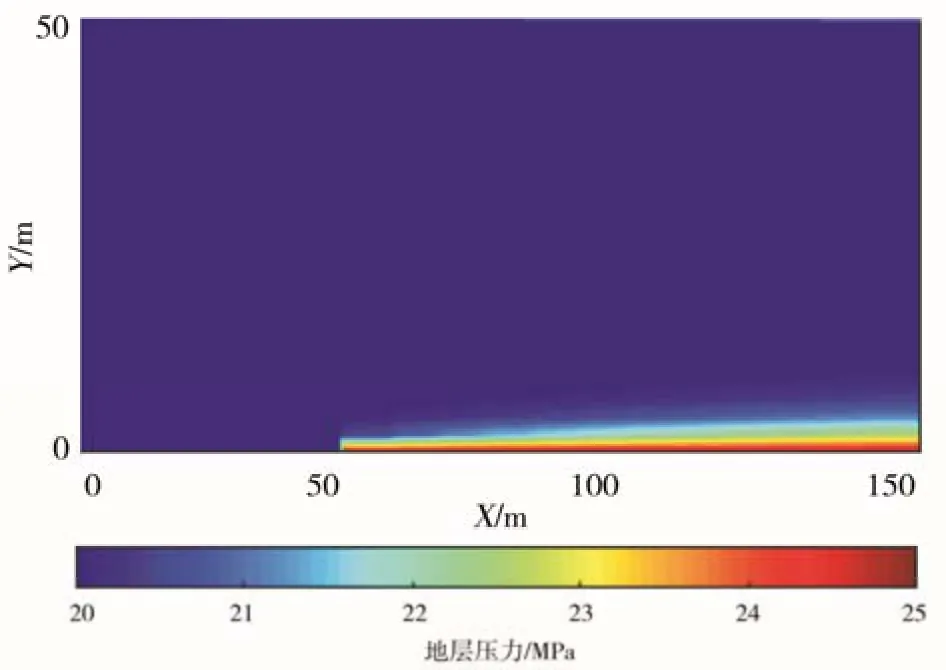
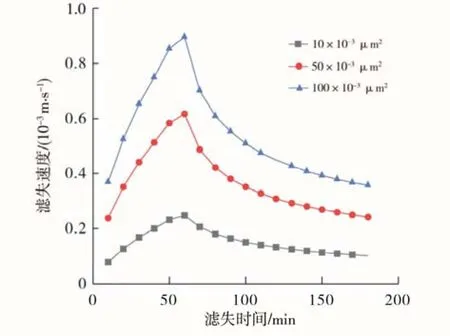
综合可得：

式中： p1，j为第一行网格节点的压力值，Pa； p2，j为第二行网格节点的压力值，Pa。

初始条件为整个求解域上的压力均为原始油藏压力，即：

求得压力分布后，根据裂缝壁面上的压力梯度即可得到裂缝壁面上的滤失速度：

式中：v 为滤失速度，10-3m/s；k 为渗透率，μm2；μ 为液体黏度，mPa·s。

可以得到整条裂缝上的平均滤失速度：

2 模型求解

为保证收敛性，本文采用古典五点隐式差分法对模型进行求解，离散后的方程如下所示：

式中：n、n+ 1分别为时间节点的编号； Δt 为时间步长，s；Δ x为 x 方向网格长度，m；Δ y 为 y 方向网格长度，m；为第n 个时间节点所有空间节点的压力值，Pa。

上式共有i×j 个未知数和i×j 个方程，构成i×j 阶的线性方程组，可由tn时刻的已知压力分布求得tn+1时刻的压力分布，如此迭代下去便能求解。

3 结果分析

考虑裂缝动态扩展后的压力分布随时间变化较大，特别是在裂缝扩展阶段，滤失前沿不断向油层深部推进，滤失区域不断扩大，与定长度裂缝的滤失情况区别较大。计算所用的参数如表1 所示，图2～4 为使用差分法编程求解得到的压力分布。图2 为裂缝扩展30 min 时的压力分布，裂缝未扩展到的地方仍然为原始油藏压力，说明扩展阶段的裂缝并不是以最终长度参与滤失。

表1 计算时所取的主要参数

图3 为裂缝扩展60 min 时的压力分布，水力裂缝长度为30 min时的2倍，压力分布范围相应更大，原先 30 min 内形成的裂缝的压力分布范围也更大。

图4 为裂缝扩展90 min 时的压力分布，裂缝扩展至研究区域边界。

由图2～4 可以明显看出，不同滤失时刻裂缝的压力影响范围不同，且裂缝越靠近初始端，对应的压力影响范围越大。

图2 裂缝扩展30 min 时的压力分布

图3 裂缝扩展60 min 时的压力分布

图4 裂缝扩展90 min 时的压力分布

考虑裂缝动态扩展后的滤失曲线与经典滤失曲线不同的是，滤失速度存在一个上升阶段，这个阶段对应裂缝扩展阶段。随着裂缝增长，滤失区域越来越大，因而滤失速度会变大，而裂缝停止增长后，滤失速度逐渐变小，此时的滤失速度变化规则与经典理论一致。

由图5 可知，地层渗透率越高，裂缝扩展阶段滤失速度能达到的峰值越高；地层渗透率较低时，滤失速度的峰值也较低，滤失速度变化较小，裂缝动态扩展的影响也较小。

图5 不同渗透率地层的滤失速度变化曲线

图6 为不同裂缝扩展速度下的滤失速度变化曲线，除了裂缝扩展速度不同，其余参数均相同。由图可知，裂缝扩展越快，滤失速度到达峰值的时间越早，且滤失速度峰值也越高。滤失速度到达峰值对应着裂缝扩展到终点，即裂缝扩展越快滤失速度达到峰值也越早；裂缝扩展速度较慢时，不仅滤失速度达到峰值的时间晚，而且由于地层进液更充分，峰值也会较小；当裂缝扩展速度极快时，滤失速度增长期极短，滤失速度曲线与定长裂缝的滤失速度曲线非常接近。因此，在脆性大、液体推进快的地层，液体的初始滤失速度会更快，这种地层若需降低初始滤失速度，可以考虑增大液体黏度、加粉砂等措施。